完全平方公式

(共13张PPT)
吴木娇
一、教材分析
二、教法与学法
三、教学设计
四、说课小结
（二）教学目标
理解公式的推导过程，了解公式的几何背景，会应用公式进行简单的计算。
（三） 教学重难点
重点：理解和掌握完全平方公式，并会运用公式进行简单的计算。
难点：判别要计算的代数式是哪两个数的和(或差)的平方。
一、创设情景，导入新课
二、合作交流，探究新知
三、观察特征，深入探究
四、范例解析，深化新知
五、畅谈收获，归纳总结
六、作业布置，延伸新知
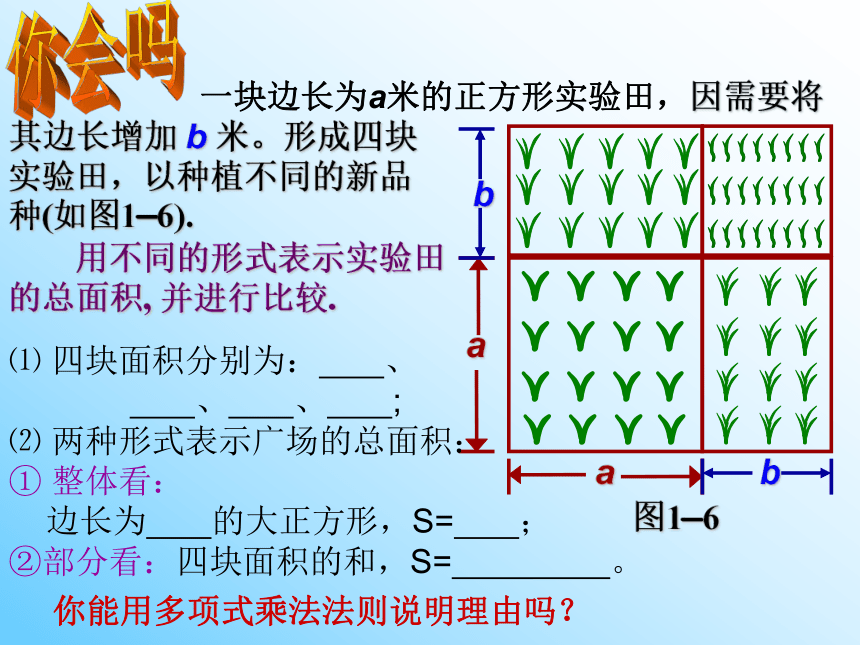
图1—6
a
一块边长为a米的正方形实验田，因需要将其边长增加 b 米。形成四块
实验田，以种植不同的新品
种(如图1—6).
用不同的形式表示实验田的总面积, 并进行比较.
a
b
b
⑴ 四块面积分别为： 、
、 、 ;
⑵ 两种形式表示广场的总面积：
① 整体看：
边长为 的大正方形，S= ；
②部分看：四块面积的和，S= 。
你能用多项式乘法法则说明理由吗？
如果将该正方形田地的边长缩减b米，
则其边长又为多少？面积呢？
(如图1—7).
a
b
a
b
(如图1—7).
用不同的形式表示实验田
的总面积, 并进行比较.
⑴ 四块面积分别为： 、
、 、 ;
⑵ 两种形式表示广场的总面积：
① 整体看：
边长为 的正方形S= ；
②部分看：S=
你能用多项式乘法法则说明理由吗？
这两个公式有何相同点与不同点？
用自己的语言叙述上面的公式
我
的
顺
口
溜
首平方，尾平方，首尾两倍中间放，合是加差是减。
例1：
练习：1、略
2、下列计算是否真确？如何改正？
例2：
(2)
(3)
练习：同桌之间相互出题练习
一、创设情景，导入新课
二、合作交流，探究新知
三、观察特征，深入探究
四、范例解析，深化新知
五、畅谈收获，归纳总结
六、作业布置，延伸新知
板书设计
15.3.2 完全平方公式
1、公式：
2、例题
3、学生板演