2020—2021学年苏科版数学八年级下册 11.2 反比例函数的图像与性质(3课时 含答案)
文档属性
| 名称 | 2020—2021学年苏科版数学八年级下册 11.2 反比例函数的图像与性质(3课时 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 461.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-03 11:36:46 | ||
图片预览




文档简介
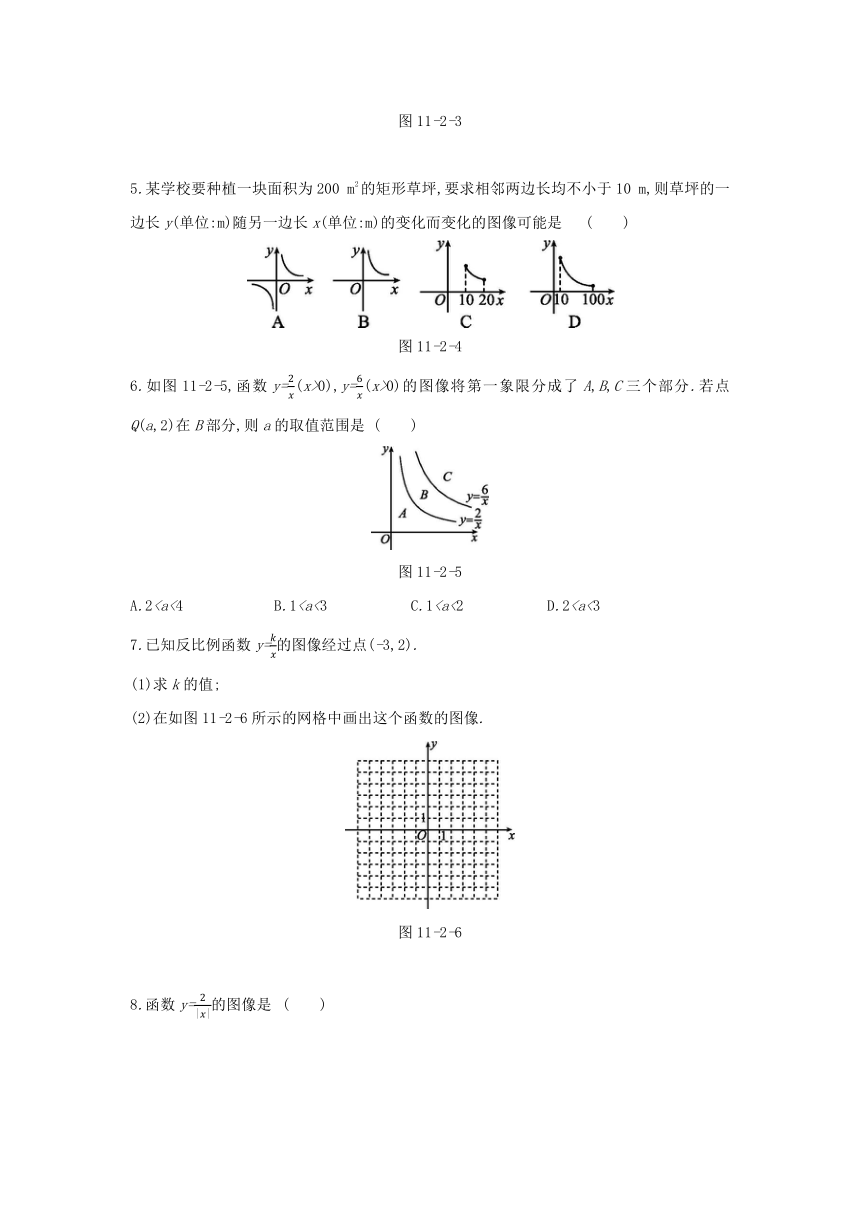
11.2 第1课时 反比例函数的图像
1.请用描点法在平面直角坐标系内画出函数y=-的图像.
(1)列表:
x
…
-3
-2
-1
1
2
3
…
y
…
…
(2)在图11-2-1中描点并连线.
2.反比例函数y=的图像大致是
( )
图11-2-2
3.对于反比例函数y=-的图像对称性的叙述,错误的是
( )
A.关于原点对称
B.关于直线y=x对称
C.关于直线y=-x对称
D.关于x轴对称
4.反比例函数y=的图像的一个分支如图11-2-3所示,则另一个分支在第 象限.?
图11-2-3
5.某学校要种植一块面积为200
m2的矩形草坪,要求相邻两边长均不小于10
m,则草坪的一边长y(单位:m)随另一边长x(单位:m)的变化而变化的图像可能是
( )
图11-2-4
6.如图11-2-5,函数y=(x>0),y=(x>0)的图像将第一象限分成了A,B,C三个部分.若点Q(a,2)在B部分,则a的取值范围是
( )
图11-2-5
A.2B.1C.1D.27.已知反比例函数y=的图像经过点(-3,2).
(1)求k的值;
(2)在如图11-2-6所示的网格中画出这个函数的图像.
图11-2-6
8.函数y=的图像是
( )
图11-2-7
1.解:(1)表格内从左到右依次填1,,3,-3,-,-1.
(2)描点、连线如图所示:
2.D
3.D
4.四
5.C [解析]
∵草坪的面积为200
m2,∴x,y存在关系y=.∵相邻两边长均不小于10
m,∴x≥10,y≥10,则10≤x≤20.故选C.
6.B [解析]
把y=2分别代入y=(x>0),y=(x>0),得x=1和x=3.∵点Q(a,2)在B部分,∴17.解:(1)把(-3,2)代入y=,得k=-3×2=-6.
(2)由(1)知,函数的表达式为y=-.根据列表、描点、连线三个步骤,可以画出图像.图略.
8.B [解析]
∵函数y=中不论x为何值,y的值均大于0,∴选项A,C,D错误,B正确.
11.2 第2课时 反比例函数的性质
1.若对于每一象限内的双曲线y=,y都随x的增大而增大,则m的取值范围是
( )
A.m>0
B.m<0
C.m≥0
D.m≤0
2.[2020·衡阳改编]
关于反比例函数y=,下列说法错误的是
( )
A.它的图像与直线y=-x无交点
B.函数图像分布在第一、三象限
C.当x>0时,y随x的增大而增大
D.当x<0时,y随x的增大而减小
3.[2020·江苏苏北地区模拟]
已知反比例函数y=的图像,在每一象限内,y随x的增大而增大,则n的取值范围是 .?
4.[2019·镇江]
已知点A(-2,y1),B(-1,y2)都在反比例函数y=-的图像上,则y1 y2.(填“>”或“<”)?
5.[2019·江阴期中]
如图11-2-8,反比例函数y=(k<0)的图像与经过原点的直线相交于A,B两点,已知点A的坐标为(-2,1),那么点B的坐标为 .?
图11-2-8
6.已知反比例函数y=.
(1)当y=-4时,求x的值;
(2)这个函数的图像在第几象限?在每一个象限内,y随x的增大怎样变化?
(3)点A-,20,B-,1在该函数的图像上吗?
7.[2019·苏州姑苏区期末]
已知点A(1,2)在反比例函数y=的图像上,则该反比例函数的表达式是
( )
A.y=
B.y=
C.y=
D.y=2x
8.[2020·云南]
已知一个反比例函数的图像经过点(3,1),若该反比例函数的图像也经过点(-1,m),则m= .?
9.某反比例函数的图像如图11-2-9所示,则此反比例函数的表达式为 .?
图11-2-9
10.如图11-2-10,矩形ABCD的边AB与y轴平行,点A的坐标为(1,m),点C的坐标为(3,m+6),那么图像同时经过点B与点D的反比例函数的表达式为 .?
图11-2-10
11.已知反比例函数y=,当x=2时,y=3.
(1)求m的值;
(2)当3≤x≤6时,求y的取值范围.
12.在同一平面直角坐标系中,函数y=mx+m(m≠0)与y=的图像可能是
( )
图11-2-11
13.[2019·安徽]
已知点A(1,-3)关于x轴的对称点A'在反比例函数y=的图像上,则实数k的值为
( )
A.3
B.
C.-3
D.-
14.如图11-2-12,△ABC的三个顶点的坐标分别为A(1,2),B(4,2),C(4,4),若反比例函数y=在第一象限内的图像与△ABC有交点,则实数k的取值范围是
( )
图11-2-12
A.2≤k≤16
B.2≤k≤8
C.1≤k≤4
D.8≤k≤16
15.设反比例函数y=,(x1,y1),(x2,y2)为其图像上的两点,当x1<0y2,则k的取值范围是 .?
16.如图11-2-13,P是反比例函数y=(x<0)的图像上的一点,PA垂直于y轴,垂足为A,PB垂直于x轴,垂足为B.若矩形PBOA的面积为6,则k的值为 .?
图11-2-13
17.已知y=y1+y2,y1与x-1成正比例,y2与x+1成反比例.当x=0时,y=-3;当x=1时,y=-1.
(1)求y关于x的函数表达式;
(2)当x=-时,求y的值.
18.如图11-2-14,点A(3,5)关于原点O的对称点为C,分别过点A,C作y轴的平行线,与反比例函数y=(0(1)求k的值;
(2)直接写出图中阴影部分的面积.
图11-2-14
19.已知反比例函数y=,其中1≤x≤2.
(1)若a<-2,函数y=的最小值是-3,求a的值;
(2)已知a>-2,函数y=的最大值与最小值之差是1,求a的值.
1.B
2.C [解析]
∵反比例函数的表达式为y=,k=2>0,∴它的图像分布在第一、三象限,与直线y=-x无交点,故A,B选项正确;∵k=2>0,∴当x>0时,y随x的增大而减小;当x<0时,y随x的增大而减小,故C错误,D正确.故选C.
3.n<-3 [解析]
∵反比例函数y=的图像,在每一象限内,y随x的增大而增大,∴n+3<0,解得n<-3.故答案为n<-3.
4.< [解析]
反比例函数y=-的图像在第二、四象限,而点A(-2,y1),B(-1,y2)都在第二象限,在第二象限内,y随x的增大而增大.∵-2<-1,∴y15.(2,-1) [解析]
∵点A与点B关于原点对称,点A的坐标为(-2,1),∴点B的坐标为(2,-1).
6.解:(1)当y=-4时,有-4=-,解得x=.
(2)这个函数的图像在第二、四象限,在每一个象限内,y随x的增大而增大.
(3)点A在该函数的图像上,点B不在该函数的图像上.
7.C [解析]
∵点A(1,2)在反比例函数y=的图像上,
∴2=,∴k=2,
∴这个反比例函数的表达式是y=.
故选C.
8.-3 [解析]
设反比例函数的表达式为y=,依据反比例函数的图像经过点(3,1)和(-1,m),即可得到k=3×1=-m,进而得出m=-3.
9.y=- [解析]
设反比例函数的表达式为y=(k为常数,k≠0).
∵反比例函数的图像过点(-3,2),
∴2=,解得k=-6,
∴反比例函数的表达式为y=-.
10.y= [解析]
∵矩形ABCD的边AB与y轴平行,A(1,m),C(3,m+6),∴B(1,m+6),D(3,m).∵点B,D在反比例函数的图像上,∴1×(m+6)=3m,解得m=3,∴B(1,9),故反比例函数的表达式为y=.
11.解:(1)把x=2,y=3代入y=,
得5-m=6,∴m=-1.
(2)由(1)知,反比例函数的表达式为y=.
当x=3时,得y=2;
当x=6时,得y=1.
当3≤x≤6时,y随x的增大而减小,
∴y的取值范围是1≤y≤2.
12.D [解析]
选项A中由反比例函数图像得m<0,则一次函数图像经过第二、三、四象限,所以A选项错误;选项B中由反比例函数图像得m>0,则一次函数图像经过第一、二、三象限,所以B选项错误;选项C中由反比例函数图像得m<0,则一次函数图像经过第二、三、四象限,所以C选项错误;选项D中由反比例函数图像得m>0,则一次函数图像经过第一、二、三象限,所以D选项正确.故选D.
13.A [解析]
点A(1,-3)关于x轴的对称点A'的坐标为(1,3),把点A'(1,3)的坐标代入y=,得k=1×3=3.故选A.
14.A [解析]
由题意,得△ABC是直角三角形,∴当反比例函数y=的图像经过点A时k最小,经过点C时k最大,∴k最小=1×2=2,k最大=4×4=16,∴2≤k≤16.故选A.
15.k<-1 [解析]
因为当x1<0y2,所以双曲线在第二、四象限,则k+1<0,解得k<-1.故答案为k<-1.
16.-6 [解析]
∵矩形PBOA的面积为6,∴|k|=6.∵反比例函数y=(x<0)的图像在第二象限,∴k<0,∴k=-6.
17.解:(1)设y1=k1(x-1)(k1为常数,且k1≠0),y
2=(k2为常数,且k2≠0).
∵y=y1+y2,∴y=k1(x-1)+.
∵当x=0时,y=-3;当x=1时,y=-1,
∴解得
∴y关于x的函数表达式为y=x-1-.
(2)当x=-时,y=x-1-=--1-=-.
18.解:(1)设直线AE的函数表达式为y=mx+b.
∵A(3,5),E(-2,0),
∴解得
∴直线AE的函数表达式为y=x+2.
∵点A(3,5)关于原点O的对称点为C,
∴点C的坐标为(-3,-5).
∵CD∥y轴,∴设点D的坐标为(-3,a),
∴a=-3+2=-1,∴点D的坐标为(-3,-1).
∵反比例函数y=(0(2)S阴影=12.
19.解:(1)∵a<-2,∴在每一象限内,y随x的增大而增大.又∵当1≤x≤2时,函数y=的最小值是-3,∴当x=1时,y=-3,则a=-3.
(2)①当-2∴-a=1,
∴a=-2(不合题意,舍去).
②当a>0时,在1≤x≤2范围内y随x的增大而减小,
∴a-=1,∴a=2.
综上所述,a的值为2.
11.2 第3课时 反比例函数的图像与性质
反比例函数的图像与性质
1.在平面直角坐标系中,反比例函数y=(k≠0)的图像在每个象限内,y随着x的增大而增大,那么它的图像的两个分支分别在
( )
A.第一、三象限
B.第二、四象限
C.第一、二象限
D.第三、四象限
2.[2019·徐州]
若点A(x1,y1),B(x2,y2)都在函数y=的图像上,且x1<0( )
A.y1B.y1=y2
C.y1>y2
D.y1=-y2
3.[2020·潍坊]
如图11-2-15,函数y=kx+b(k≠0)与y=(m≠0)的图像相交于A(-2,3),B(1,-6)两点,则关于x的不等式kx+b>的解集为
( )
图11-2-15
A.x>-2
B.-21
C.x>1
D.x<-2或04.已知直线y=ax(a≠0)与双曲线y=(k≠0)的一个交点的坐标为(2,4),则它们另一个交点的坐标是 .?
5.[2020·泰州模拟]
若反比例函数y=的图像经过第一、三象限,则k的取值范围是 .?
6.[2019·龙东地区改编]
如图11-2-16,在平面直角坐标系中,O为坐标原点,平行四边形OABC的顶点A在反比例函数y=的图像上,顶点B在反比例函数y=的图像上,点C在x轴的正半轴上,则平行四边形OABC的面积是 .?
图11-2-16
7.已知y是x的反比例函数,且当x=2时,y=-3.
(1)求y与x之间的函数表达式;
(2)在如图11-2-17所示的平面直角坐标系中画出这个函数的图像;
(3)试判断点P(-2,3)是否在这个函数的图像上.
图11-2-17
8.[2019·贵港]
如图11-2-18,菱形ABCD的边AB在x轴上,点A的坐标为(1,0),点D(4,4)在反比例函数y=(x>0)的图像上,直线y=x+b经过点C,与y轴交于点E,连接AC,AE.
(1)求k,b的值;
(2)求△ACE的面积.
图11-2-18
9.如图11-2-19,一次函数y1=k1x+b(k1≠0)的图像分别与x轴,y轴相交于点A,B,与反比例函数y2=(k2≠0)的图像相交于点C(-4,-2),D(2,4).
(1)求一次函数和反比例函数的表达式;
(2)当x为何值时,y1>0?
(3)当x为何值时,y1图11-2-19
10.若反比例函数y=(k≠0),当x>0时,y随x的增大而减小,则一次函数y=kx-k的图像经过的象限是
( )
A.第一、二、三象限
B.第一、二、四象限
C.第一、三、四象限
D.第二、三、四象限
11.如图11-2-20,在平面直角坐标系中,线段AB的两个端点分别在坐标轴上,点A的坐标为(1,0),将线段AB绕点A顺时针旋转90°后,点B恰好落在反比例函数y=的图像在第一象限内的分支上的点B'处,则点B的坐标为
( )
图11-2-20
A.(0,2)
B.(0,3)
C.(0,4)
D.(0,5)
12.已知正比例函数y=-4x与反比例函数y=(k≠0)的图像交于A,B两点.若点A的坐标为(m,4),则点B的坐标为 .?
13.[2019·北京]
在平面直角坐标系xOy中,点A(a,b)(a>0,b>0)在双曲线y=上,点A关于x轴的对称点B在双曲线y=上,则k1+k2的值为 .?
14.如图11-2-21,反比例函数y=
和y=-
的图像分别是l1和l2.设点P在双曲线l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为 .?
图11-2-21
15.如图11-2-22,点A(m,6),B(n,1)在反比例函数的图像上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
(1)求m,n的值并写出反比例函数的表达式.
(2)连接AB,在线段DC上是否存在一点E,使△ABE的面积等于5?若存在,求出点E的坐标;若不存在,请说明理由.
图11-2-22
16.已知反比例函数y=(m为常数)的图像在第一、三象限.
(1)求m的取值范围.
(2)如图11-2-23,若该反比例函数的图像经过?ABOD的顶点D,点A,B的坐标分别为(0,3),(-2,0).
①求该反比例函数的表达式.
②设P是该反比例函数图像上的一点,若OD=OP,则点P的坐标为 ;若以D,O,P为顶点的三角形是等腰三角形,则满足条件的点P有 个.?
图11-2-23
1.B [解析]
∵反比例函数y=(k≠0)的图像在每个象限内y随着x的增大而增大,∴k<0,∴它的图像的两个分支分别在第二、四象限.故选B.
2.A [解析]
由函数y=知该函数的图像在第一、三象限、在每个象限内y随x的增大而减小.∵点A(x1,y1),B(x2,y2)都在函数y=的图像上,且x1<03.D [解析]
观察图像可知,当x<-2或0.故选D.
4.(-2,-4) [解析]
∵反比例函数的图像与经过原点的直线的两个交点一定关于原点对称,∴另一个交点与点(2,4)关于原点对称,∴该点的坐标为(-2,-4).
5.k< [解析]
∵反比例函数的图像经过第一、三象限,∴1-3k>0,解得k<.
6.4
7.解:(1)设y与x之间的函数表达式为y=(k≠0).
∵当x=2时,y=-3,
∴-3=,解得k=-6,
∴y与x之间的函数表达式为y=-.
(2)略.
(3)当x=-2时,y=-=3,
∴点P(-2,3)在这个函数的图像上.
8.解:(1)由已知可得AD==5.
∵四边形ABCD为菱形,D(4,4),∴C(9,4).
∵点D(4,4)在反比例函数y=(x>0)的图像上,∴k=16.
将点C(9,4)的坐标代入y=x+b,得4=×9+b,解得b=-2.
(2)当x=0时,y=x-2=-2,当y=0时,0=x-2,解得x=3,∴E(0,-2),直线y=x-2与x轴的交点坐标为(3,0),
∴S△ACE=×2×(2+4)=6.
9.解:(1)∵一次函数y1=k1x+b的图像经过点C(-4,-2),D(2,4),
∴解得
∴一次函数的表达式为y1=x+2.
∵反比例函数y2=的图像经过点D(2,4),∴4=,∴k2=8,
∴反比例函数的表达式为y2=.
(2)由y1>0,得x+2>0,
∴x>-2,∴当x>-2时,y1>0.
(3)x<-4或010.C [解析]
根据反比例函数和一次函数图像的性质作答.
要判断一次函数y=kx-k的图像的位置,需要知道k的符号.由已知y=,当x>0时,y随x的增大而减小,得k>0.对于一次函数y=kx-k,当k>0时,直线呈上升趋势,而-k<0时,直线交y轴于负半轴,所以它的图像经过第一、三、四象限.故选C.
[点评]
不论正比例函数还是反比例函数,我们既要能从图像判断其性质,也要能从已知的性质判断其图像的位置.另外,题目中的一次函数y=kx-k中的-k相当于一次函数一般式y=kx+b中的b.
11.B [解析]
∵点A的坐标为(1,0),将线段AB绕点A顺时针旋转90°后,点B恰好落在反比例函数y=的图像在第一象限内的分支上的点B'处,∴点B'的纵坐标是1.当y=1时,1=,得x=4,∴点B'的坐标是(4,1),∴点B的坐标是(0,3).故选B.
12.(1,-4) [解析]
∵正比例函数y=-4x与反比例函数y=的图像交于A,B两点,点A的坐标为(m,4),
∴4=-4m,解得m=-1,∴A(-1,4).
∵反比例函数与正比例函数的图像均关于原点对称,∴B(1,-4).
13.0 [解析]
∵A,B两点关于x轴对称,
∴点B的坐标为(a,-b).
∵A(a,b),B(a,-b)两点分别在双曲线y=和y=上,∴ab=k1,-ab=k2,∴k1+k2=0.故答案为0.
14. [解析]
∵点P在双曲线y=上,
∴设点P的坐标是a,.
∵PA⊥x轴,∴点A的横坐标是a.
∵点A在函数y=-的图像上,
∴点A的坐标是a,-.
∵PB⊥y轴,∴点B的纵坐标是.
∵点B在函数y=-的图像上,
∴将点B的纵坐标代入,得=-
,
解得x=-2a,∴点B的坐标是-2a,,
∴PA=--=
,PB=|a-(-2a)|=|3a|.
∵PA⊥x轴,PB⊥y轴,x轴⊥y轴,
∴PA⊥PB,
∴△PAB的面积是PA·PB=
××|3a|=.
15.解:(1)由题意,得解得
∴m,n的值分别为1,6.
设反比例函数的表达式为y=(k≠0).
将点A(1,6)的坐标代入y=,得k=xy=1×6=6,
∴反比例函数的表达式为y=.
(2)存在.
设点E的坐标为(x,0),则DE=x-1,CE=6-x.
∵AD⊥x轴,BC⊥x轴,
∴∠ADE=∠BCE=90°,
∴△ADE和△BCE均是直角三角形,
∴S△ABE=S梯形ABCD-S△ADE-S△BCE
=(BC+AD)·DC-DE·AD-CE·BC
=×(1+6)×5-(x-1)×6-(6-x)×1
=-x=5,
解得x=5.
∴点E的坐标为(5,0).
16.解:(1)由题意知1-2m>0,解得m<.
(2)①∵四边形ABOD是平行四边形,
∴AD∥BO且AD=BO.
∵A(0,3),B(-2,0),∴点D的坐标是(2,3),
∴=3,即1-2m=6,
∴该反比例函数的表达式为y=.
②(3,2)或(-2,-3)或(-3,-2) 4
1.请用描点法在平面直角坐标系内画出函数y=-的图像.
(1)列表:
x
…
-3
-2
-1
1
2
3
…
y
…
…
(2)在图11-2-1中描点并连线.
2.反比例函数y=的图像大致是
( )
图11-2-2
3.对于反比例函数y=-的图像对称性的叙述,错误的是
( )
A.关于原点对称
B.关于直线y=x对称
C.关于直线y=-x对称
D.关于x轴对称
4.反比例函数y=的图像的一个分支如图11-2-3所示,则另一个分支在第 象限.?
图11-2-3
5.某学校要种植一块面积为200
m2的矩形草坪,要求相邻两边长均不小于10
m,则草坪的一边长y(单位:m)随另一边长x(单位:m)的变化而变化的图像可能是
( )
图11-2-4
6.如图11-2-5,函数y=(x>0),y=(x>0)的图像将第一象限分成了A,B,C三个部分.若点Q(a,2)在B部分,则a的取值范围是
( )
图11-2-5
A.2
(1)求k的值;
(2)在如图11-2-6所示的网格中画出这个函数的图像.
图11-2-6
8.函数y=的图像是
( )
图11-2-7
1.解:(1)表格内从左到右依次填1,,3,-3,-,-1.
(2)描点、连线如图所示:
2.D
3.D
4.四
5.C [解析]
∵草坪的面积为200
m2,∴x,y存在关系y=.∵相邻两边长均不小于10
m,∴x≥10,y≥10,则10≤x≤20.故选C.
6.B [解析]
把y=2分别代入y=(x>0),y=(x>0),得x=1和x=3.∵点Q(a,2)在B部分,∴1
(2)由(1)知,函数的表达式为y=-.根据列表、描点、连线三个步骤,可以画出图像.图略.
8.B [解析]
∵函数y=中不论x为何值,y的值均大于0,∴选项A,C,D错误,B正确.
11.2 第2课时 反比例函数的性质
1.若对于每一象限内的双曲线y=,y都随x的增大而增大,则m的取值范围是
( )
A.m>0
B.m<0
C.m≥0
D.m≤0
2.[2020·衡阳改编]
关于反比例函数y=,下列说法错误的是
( )
A.它的图像与直线y=-x无交点
B.函数图像分布在第一、三象限
C.当x>0时,y随x的增大而增大
D.当x<0时,y随x的增大而减小
3.[2020·江苏苏北地区模拟]
已知反比例函数y=的图像,在每一象限内,y随x的增大而增大,则n的取值范围是 .?
4.[2019·镇江]
已知点A(-2,y1),B(-1,y2)都在反比例函数y=-的图像上,则y1 y2.(填“>”或“<”)?
5.[2019·江阴期中]
如图11-2-8,反比例函数y=(k<0)的图像与经过原点的直线相交于A,B两点,已知点A的坐标为(-2,1),那么点B的坐标为 .?
图11-2-8
6.已知反比例函数y=.
(1)当y=-4时,求x的值;
(2)这个函数的图像在第几象限?在每一个象限内,y随x的增大怎样变化?
(3)点A-,20,B-,1在该函数的图像上吗?
7.[2019·苏州姑苏区期末]
已知点A(1,2)在反比例函数y=的图像上,则该反比例函数的表达式是
( )
A.y=
B.y=
C.y=
D.y=2x
8.[2020·云南]
已知一个反比例函数的图像经过点(3,1),若该反比例函数的图像也经过点(-1,m),则m= .?
9.某反比例函数的图像如图11-2-9所示,则此反比例函数的表达式为 .?
图11-2-9
10.如图11-2-10,矩形ABCD的边AB与y轴平行,点A的坐标为(1,m),点C的坐标为(3,m+6),那么图像同时经过点B与点D的反比例函数的表达式为 .?
图11-2-10
11.已知反比例函数y=,当x=2时,y=3.
(1)求m的值;
(2)当3≤x≤6时,求y的取值范围.
12.在同一平面直角坐标系中,函数y=mx+m(m≠0)与y=的图像可能是
( )
图11-2-11
13.[2019·安徽]
已知点A(1,-3)关于x轴的对称点A'在反比例函数y=的图像上,则实数k的值为
( )
A.3
B.
C.-3
D.-
14.如图11-2-12,△ABC的三个顶点的坐标分别为A(1,2),B(4,2),C(4,4),若反比例函数y=在第一象限内的图像与△ABC有交点,则实数k的取值范围是
( )
图11-2-12
A.2≤k≤16
B.2≤k≤8
C.1≤k≤4
D.8≤k≤16
15.设反比例函数y=,(x1,y1),(x2,y2)为其图像上的两点,当x1<0
16.如图11-2-13,P是反比例函数y=(x<0)的图像上的一点,PA垂直于y轴,垂足为A,PB垂直于x轴,垂足为B.若矩形PBOA的面积为6,则k的值为 .?
图11-2-13
17.已知y=y1+y2,y1与x-1成正比例,y2与x+1成反比例.当x=0时,y=-3;当x=1时,y=-1.
(1)求y关于x的函数表达式;
(2)当x=-时,求y的值.
18.如图11-2-14,点A(3,5)关于原点O的对称点为C,分别过点A,C作y轴的平行线,与反比例函数y=(0
(2)直接写出图中阴影部分的面积.
图11-2-14
19.已知反比例函数y=,其中1≤x≤2.
(1)若a<-2,函数y=的最小值是-3,求a的值;
(2)已知a>-2,函数y=的最大值与最小值之差是1,求a的值.
1.B
2.C [解析]
∵反比例函数的表达式为y=,k=2>0,∴它的图像分布在第一、三象限,与直线y=-x无交点,故A,B选项正确;∵k=2>0,∴当x>0时,y随x的增大而减小;当x<0时,y随x的增大而减小,故C错误,D正确.故选C.
3.n<-3 [解析]
∵反比例函数y=的图像,在每一象限内,y随x的增大而增大,∴n+3<0,解得n<-3.故答案为n<-3.
4.< [解析]
反比例函数y=-的图像在第二、四象限,而点A(-2,y1),B(-1,y2)都在第二象限,在第二象限内,y随x的增大而增大.∵-2<-1,∴y1
∵点A与点B关于原点对称,点A的坐标为(-2,1),∴点B的坐标为(2,-1).
6.解:(1)当y=-4时,有-4=-,解得x=.
(2)这个函数的图像在第二、四象限,在每一个象限内,y随x的增大而增大.
(3)点A在该函数的图像上,点B不在该函数的图像上.
7.C [解析]
∵点A(1,2)在反比例函数y=的图像上,
∴2=,∴k=2,
∴这个反比例函数的表达式是y=.
故选C.
8.-3 [解析]
设反比例函数的表达式为y=,依据反比例函数的图像经过点(3,1)和(-1,m),即可得到k=3×1=-m,进而得出m=-3.
9.y=- [解析]
设反比例函数的表达式为y=(k为常数,k≠0).
∵反比例函数的图像过点(-3,2),
∴2=,解得k=-6,
∴反比例函数的表达式为y=-.
10.y= [解析]
∵矩形ABCD的边AB与y轴平行,A(1,m),C(3,m+6),∴B(1,m+6),D(3,m).∵点B,D在反比例函数的图像上,∴1×(m+6)=3m,解得m=3,∴B(1,9),故反比例函数的表达式为y=.
11.解:(1)把x=2,y=3代入y=,
得5-m=6,∴m=-1.
(2)由(1)知,反比例函数的表达式为y=.
当x=3时,得y=2;
当x=6时,得y=1.
当3≤x≤6时,y随x的增大而减小,
∴y的取值范围是1≤y≤2.
12.D [解析]
选项A中由反比例函数图像得m<0,则一次函数图像经过第二、三、四象限,所以A选项错误;选项B中由反比例函数图像得m>0,则一次函数图像经过第一、二、三象限,所以B选项错误;选项C中由反比例函数图像得m<0,则一次函数图像经过第二、三、四象限,所以C选项错误;选项D中由反比例函数图像得m>0,则一次函数图像经过第一、二、三象限,所以D选项正确.故选D.
13.A [解析]
点A(1,-3)关于x轴的对称点A'的坐标为(1,3),把点A'(1,3)的坐标代入y=,得k=1×3=3.故选A.
14.A [解析]
由题意,得△ABC是直角三角形,∴当反比例函数y=的图像经过点A时k最小,经过点C时k最大,∴k最小=1×2=2,k最大=4×4=16,∴2≤k≤16.故选A.
15.k<-1 [解析]
因为当x1<0
16.-6 [解析]
∵矩形PBOA的面积为6,∴|k|=6.∵反比例函数y=(x<0)的图像在第二象限,∴k<0,∴k=-6.
17.解:(1)设y1=k1(x-1)(k1为常数,且k1≠0),y
2=(k2为常数,且k2≠0).
∵y=y1+y2,∴y=k1(x-1)+.
∵当x=0时,y=-3;当x=1时,y=-1,
∴解得
∴y关于x的函数表达式为y=x-1-.
(2)当x=-时,y=x-1-=--1-=-.
18.解:(1)设直线AE的函数表达式为y=mx+b.
∵A(3,5),E(-2,0),
∴解得
∴直线AE的函数表达式为y=x+2.
∵点A(3,5)关于原点O的对称点为C,
∴点C的坐标为(-3,-5).
∵CD∥y轴,∴设点D的坐标为(-3,a),
∴a=-3+2=-1,∴点D的坐标为(-3,-1).
∵反比例函数y=(0
19.解:(1)∵a<-2,∴在每一象限内,y随x的增大而增大.又∵当1≤x≤2时,函数y=的最小值是-3,∴当x=1时,y=-3,则a=-3.
(2)①当-2
∴a=-2(不合题意,舍去).
②当a>0时,在1≤x≤2范围内y随x的增大而减小,
∴a-=1,∴a=2.
综上所述,a的值为2.
11.2 第3课时 反比例函数的图像与性质
反比例函数的图像与性质
1.在平面直角坐标系中,反比例函数y=(k≠0)的图像在每个象限内,y随着x的增大而增大,那么它的图像的两个分支分别在
( )
A.第一、三象限
B.第二、四象限
C.第一、二象限
D.第三、四象限
2.[2019·徐州]
若点A(x1,y1),B(x2,y2)都在函数y=的图像上,且x1<0
A.y1
C.y1>y2
D.y1=-y2
3.[2020·潍坊]
如图11-2-15,函数y=kx+b(k≠0)与y=(m≠0)的图像相交于A(-2,3),B(1,-6)两点,则关于x的不等式kx+b>的解集为
( )
图11-2-15
A.x>-2
B.-2
C.x>1
D.x<-2或0
5.[2020·泰州模拟]
若反比例函数y=的图像经过第一、三象限,则k的取值范围是 .?
6.[2019·龙东地区改编]
如图11-2-16,在平面直角坐标系中,O为坐标原点,平行四边形OABC的顶点A在反比例函数y=的图像上,顶点B在反比例函数y=的图像上,点C在x轴的正半轴上,则平行四边形OABC的面积是 .?
图11-2-16
7.已知y是x的反比例函数,且当x=2时,y=-3.
(1)求y与x之间的函数表达式;
(2)在如图11-2-17所示的平面直角坐标系中画出这个函数的图像;
(3)试判断点P(-2,3)是否在这个函数的图像上.
图11-2-17
8.[2019·贵港]
如图11-2-18,菱形ABCD的边AB在x轴上,点A的坐标为(1,0),点D(4,4)在反比例函数y=(x>0)的图像上,直线y=x+b经过点C,与y轴交于点E,连接AC,AE.
(1)求k,b的值;
(2)求△ACE的面积.
图11-2-18
9.如图11-2-19,一次函数y1=k1x+b(k1≠0)的图像分别与x轴,y轴相交于点A,B,与反比例函数y2=(k2≠0)的图像相交于点C(-4,-2),D(2,4).
(1)求一次函数和反比例函数的表达式;
(2)当x为何值时,y1>0?
(3)当x为何值时,y1
10.若反比例函数y=(k≠0),当x>0时,y随x的增大而减小,则一次函数y=kx-k的图像经过的象限是
( )
A.第一、二、三象限
B.第一、二、四象限
C.第一、三、四象限
D.第二、三、四象限
11.如图11-2-20,在平面直角坐标系中,线段AB的两个端点分别在坐标轴上,点A的坐标为(1,0),将线段AB绕点A顺时针旋转90°后,点B恰好落在反比例函数y=的图像在第一象限内的分支上的点B'处,则点B的坐标为
( )
图11-2-20
A.(0,2)
B.(0,3)
C.(0,4)
D.(0,5)
12.已知正比例函数y=-4x与反比例函数y=(k≠0)的图像交于A,B两点.若点A的坐标为(m,4),则点B的坐标为 .?
13.[2019·北京]
在平面直角坐标系xOy中,点A(a,b)(a>0,b>0)在双曲线y=上,点A关于x轴的对称点B在双曲线y=上,则k1+k2的值为 .?
14.如图11-2-21,反比例函数y=
和y=-
的图像分别是l1和l2.设点P在双曲线l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为 .?
图11-2-21
15.如图11-2-22,点A(m,6),B(n,1)在反比例函数的图像上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
(1)求m,n的值并写出反比例函数的表达式.
(2)连接AB,在线段DC上是否存在一点E,使△ABE的面积等于5?若存在,求出点E的坐标;若不存在,请说明理由.
图11-2-22
16.已知反比例函数y=(m为常数)的图像在第一、三象限.
(1)求m的取值范围.
(2)如图11-2-23,若该反比例函数的图像经过?ABOD的顶点D,点A,B的坐标分别为(0,3),(-2,0).
①求该反比例函数的表达式.
②设P是该反比例函数图像上的一点,若OD=OP,则点P的坐标为 ;若以D,O,P为顶点的三角形是等腰三角形,则满足条件的点P有 个.?
图11-2-23
1.B [解析]
∵反比例函数y=(k≠0)的图像在每个象限内y随着x的增大而增大,∴k<0,∴它的图像的两个分支分别在第二、四象限.故选B.
2.A [解析]
由函数y=知该函数的图像在第一、三象限、在每个象限内y随x的增大而减小.∵点A(x1,y1),B(x2,y2)都在函数y=的图像上,且x1<0
观察图像可知,当x<-2或0
4.(-2,-4) [解析]
∵反比例函数的图像与经过原点的直线的两个交点一定关于原点对称,∴另一个交点与点(2,4)关于原点对称,∴该点的坐标为(-2,-4).
5.k< [解析]
∵反比例函数的图像经过第一、三象限,∴1-3k>0,解得k<.
6.4
7.解:(1)设y与x之间的函数表达式为y=(k≠0).
∵当x=2时,y=-3,
∴-3=,解得k=-6,
∴y与x之间的函数表达式为y=-.
(2)略.
(3)当x=-2时,y=-=3,
∴点P(-2,3)在这个函数的图像上.
8.解:(1)由已知可得AD==5.
∵四边形ABCD为菱形,D(4,4),∴C(9,4).
∵点D(4,4)在反比例函数y=(x>0)的图像上,∴k=16.
将点C(9,4)的坐标代入y=x+b,得4=×9+b,解得b=-2.
(2)当x=0时,y=x-2=-2,当y=0时,0=x-2,解得x=3,∴E(0,-2),直线y=x-2与x轴的交点坐标为(3,0),
∴S△ACE=×2×(2+4)=6.
9.解:(1)∵一次函数y1=k1x+b的图像经过点C(-4,-2),D(2,4),
∴解得
∴一次函数的表达式为y1=x+2.
∵反比例函数y2=的图像经过点D(2,4),∴4=,∴k2=8,
∴反比例函数的表达式为y2=.
(2)由y1>0,得x+2>0,
∴x>-2,∴当x>-2时,y1>0.
(3)x<-4或0
根据反比例函数和一次函数图像的性质作答.
要判断一次函数y=kx-k的图像的位置,需要知道k的符号.由已知y=,当x>0时,y随x的增大而减小,得k>0.对于一次函数y=kx-k,当k>0时,直线呈上升趋势,而-k<0时,直线交y轴于负半轴,所以它的图像经过第一、三、四象限.故选C.
[点评]
不论正比例函数还是反比例函数,我们既要能从图像判断其性质,也要能从已知的性质判断其图像的位置.另外,题目中的一次函数y=kx-k中的-k相当于一次函数一般式y=kx+b中的b.
11.B [解析]
∵点A的坐标为(1,0),将线段AB绕点A顺时针旋转90°后,点B恰好落在反比例函数y=的图像在第一象限内的分支上的点B'处,∴点B'的纵坐标是1.当y=1时,1=,得x=4,∴点B'的坐标是(4,1),∴点B的坐标是(0,3).故选B.
12.(1,-4) [解析]
∵正比例函数y=-4x与反比例函数y=的图像交于A,B两点,点A的坐标为(m,4),
∴4=-4m,解得m=-1,∴A(-1,4).
∵反比例函数与正比例函数的图像均关于原点对称,∴B(1,-4).
13.0 [解析]
∵A,B两点关于x轴对称,
∴点B的坐标为(a,-b).
∵A(a,b),B(a,-b)两点分别在双曲线y=和y=上,∴ab=k1,-ab=k2,∴k1+k2=0.故答案为0.
14. [解析]
∵点P在双曲线y=上,
∴设点P的坐标是a,.
∵PA⊥x轴,∴点A的横坐标是a.
∵点A在函数y=-的图像上,
∴点A的坐标是a,-.
∵PB⊥y轴,∴点B的纵坐标是.
∵点B在函数y=-的图像上,
∴将点B的纵坐标代入,得=-
,
解得x=-2a,∴点B的坐标是-2a,,
∴PA=--=
,PB=|a-(-2a)|=|3a|.
∵PA⊥x轴,PB⊥y轴,x轴⊥y轴,
∴PA⊥PB,
∴△PAB的面积是PA·PB=
××|3a|=.
15.解:(1)由题意,得解得
∴m,n的值分别为1,6.
设反比例函数的表达式为y=(k≠0).
将点A(1,6)的坐标代入y=,得k=xy=1×6=6,
∴反比例函数的表达式为y=.
(2)存在.
设点E的坐标为(x,0),则DE=x-1,CE=6-x.
∵AD⊥x轴,BC⊥x轴,
∴∠ADE=∠BCE=90°,
∴△ADE和△BCE均是直角三角形,
∴S△ABE=S梯形ABCD-S△ADE-S△BCE
=(BC+AD)·DC-DE·AD-CE·BC
=×(1+6)×5-(x-1)×6-(6-x)×1
=-x=5,
解得x=5.
∴点E的坐标为(5,0).
16.解:(1)由题意知1-2m>0,解得m<.
(2)①∵四边形ABOD是平行四边形,
∴AD∥BO且AD=BO.
∵A(0,3),B(-2,0),∴点D的坐标是(2,3),
∴=3,即1-2m=6,
∴该反比例函数的表达式为y=.
②(3,2)或(-2,-3)或(-3,-2) 4
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
