8.5怎样判定三角形相似（1）课件

(共19张PPT)
怎样判定
三角形相似(1)
学习目标：
1、经历判定两个三角形相似条件的探索过程，
积累数学活动的经验。
2、学会两个三角形相似的判定方法1,利用三
角形的相似解决一些简单的实际问题。
3、在运用判定方法1的过程中，能够有条理的
思考并进行简单的推理。
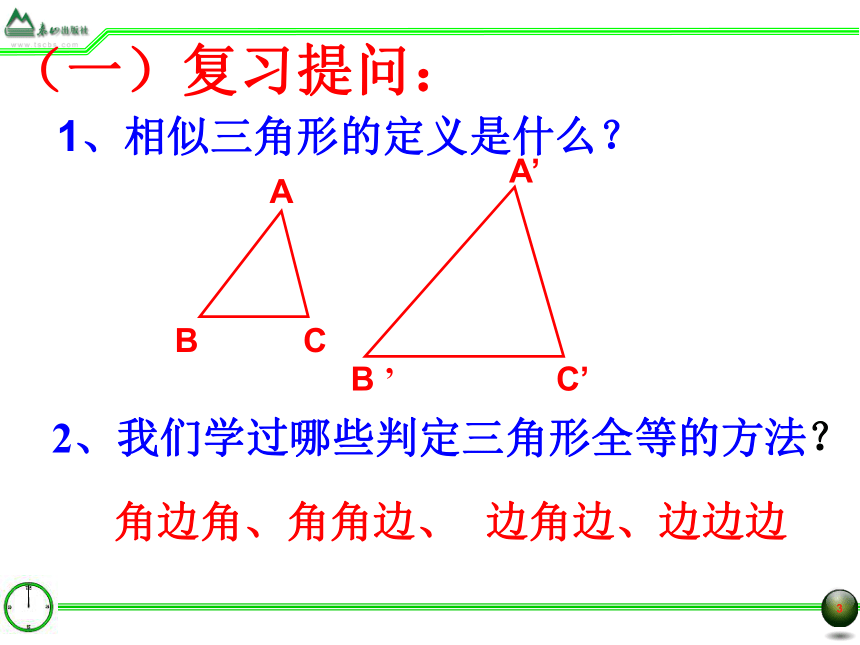
（一）复习提问：
1、相似三角形的定义是什么？
2、我们学过哪些判定三角形全等的方法？
A
B
C
A’
B ’
C’
角边角、角角边、
边角边、边边边
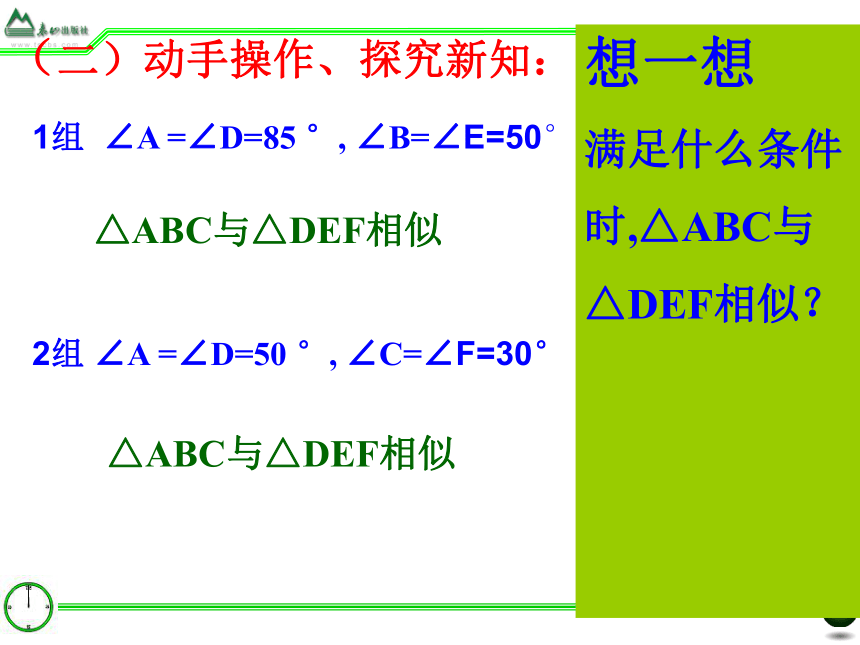
（二）动手操作、探究新知：
1组 ∠A =∠D=85 °, ∠B=∠E=50°
2组 ∠A =∠D=50 °, ∠C=∠F=30°
△ABC与△DEF相似
△ABC与△DEF相似
想一想
满足什么条件
时,△ABC与
△DEF相似？
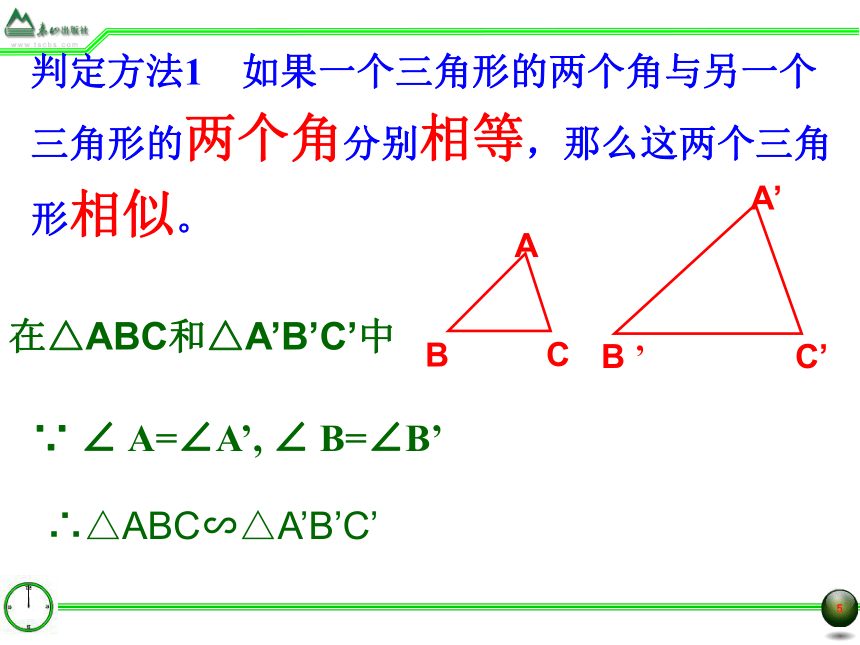
判定方法1 如果一个三角形的两个角与另一个
三角形的两个角分别相等，那么这两个三角
形相似。
A
B
C
A’
B ’
C’
在△ABC和△A’B’C’中
∴△ABC∽△A’B’C’
∵ ∠ A=∠A’, ∠ B=∠B’
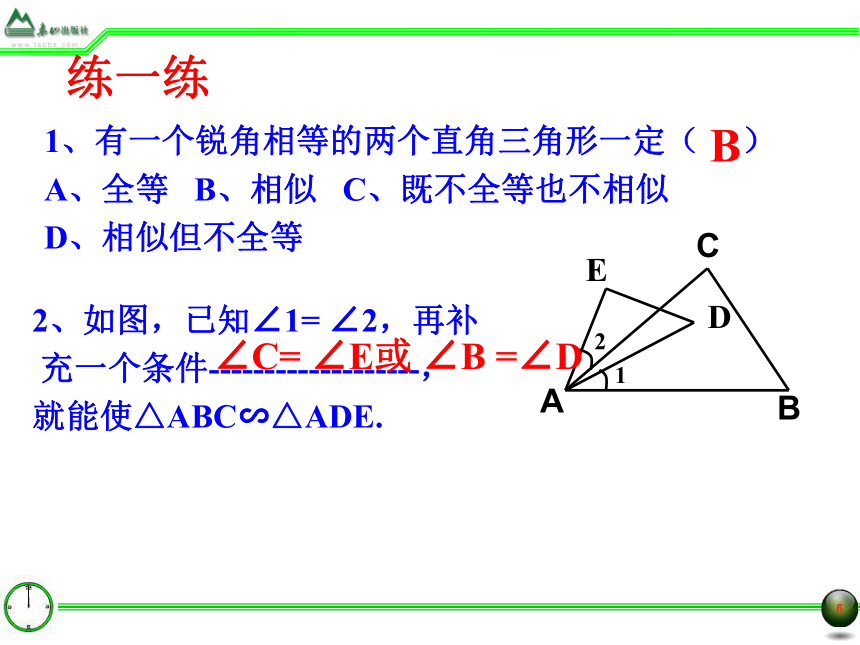
练一练
1、有一个锐角相等的两个直角三角形一定（ ）
A、全等 B、相似 C、既不全等也不相似
D、相似但不全等
C
A
B
D
E
1
2
2、如图，已知∠1= ∠2，再补
充一个条件-------------------，
就能使△ABC∽△ADE.
B
∠C= ∠E或 ∠B =∠D
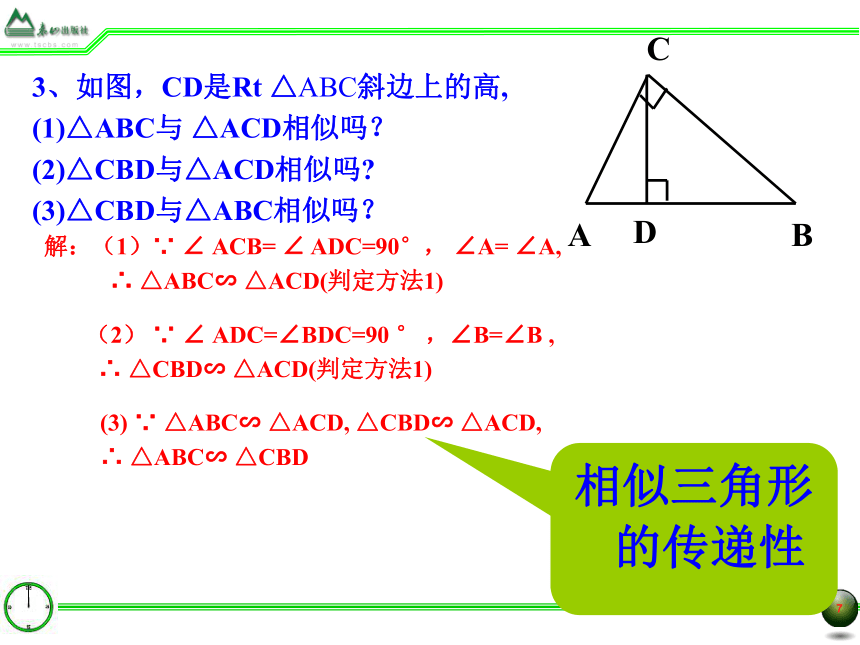
3、如图，CD是Rt △ABC斜边上的高,
△ABC与 △ACD相似吗？
△CBD与△ACD相似吗
△CBD与△ABC相似吗？
C
A
B
D
解：（1）∵ ∠ ACB= ∠ ADC=90°， ∠A= ∠A,
∴ △ABC∽ △ACD(判定方法1)
（2） ∵ ∠ ADC=∠BDC=90 ° ，∠B=∠B ,
∴ △CBD∽ △ACD(判定方法1)
(3) ∵ △ABC∽ △ACD, △CBD∽ △ACD,
∴ △ABC∽ △CBD
相似三角形的传递性
４、如图，BC∥DE, △ABC 与△ADE相似吗？
Ａ
Ｄ
Ｅ
Ｂ
Ｃ
Ａ
Ｂ
Ｃ
Ｄ
Ｅ
平行于三角形一边的直线和其他两边
（或两边的延长线）相交，
所构成的三角形与原三角形相似。
B
A
C
E
D
例题讲解
两个角
相等
三角形
相似
对应边
成比例
解决
问题
做一做
你会利用镜面反射测量电线杆的高度吗？
A
B
C
D
O
解：如图， ∵AB⊥BD,CD ⊥BD,
∴AB∥CD, ∴ △ABO∽△CDO,
∴ ∽
∴只要测量小亮的身高AB和小亮到
镜子的距离BO及镜子到电线杆的距
离DO就可以。
达标检测
1、如图，AC∥EF∥BD,则图中与
△OEF相似的三角形有( 　)
A 1个 B 2个 C 3个 D4个
2、如图，在直角梯形ABCD中,BC⊥AB,BD⊥AD,CD∥AB,
且BD=3，CD=2，则下底AB的长是———。
A
B
C
D
O
E
F
A
B
C
D
Ｂ
3、如图，在△ABC中， ∠ C=90°，BC=6，D,E分别在AB,
AC上，将△ ABC沿DE折叠，使点A落在点A’处，若A’为CE
的中点，求折痕DE的长。
A
B
C
D
E
A’
4、如图，河的对岸各有一根电线杆A,B.怎样利用相似
三角形的知识，在河的一边（如电线杆A的一边）
测得AB间的距离？请设计一个方案，并画图说明。
A·
·B
D
C
o
解：连接A、B，在岸的一边找一点O，连接AO并
延长AO到C,过点C作线段AB的平行线交BO的延
长线于点D。
∵AB∥CD,
∴ ∠A =∠C, ∠B= ∠D
∴ △ABO ∽△CDO
∴ =
所以，只要测量CD、AO、CO的之间的距离就可以。
如图，在△ABC中，AB=AC, ∠A=36°，BD
是∠ABC的角平分线，
试利用三角形相似关系证明
=AC·CD
解： ∵ ∠A =36 ° ， AB=AC ，
∴ ∠ABC =∠C=72 °
又∵BD平分∠ABC，
∴ ∠ABD= ∠CBD=36 °∴AD=BD=BC
在△ABC 和△BCD中， ∠A =∠CBD =36 °，
∠C= ∠C,
∴ △ABC ∽ △ABC(判定方法1)
∴ = ∴ =AB·CD
又∵BC=AD,AB=AC, ∴ =AC·CD
拓展延伸
A
B
C
D
作业：
必做题：课本第42页第1题，
第48页第2、3题。
选做题：练习册第16页第8题。
想一想
驶向胜利的彼岸
不经历风雨，怎么见彩虹
没有人能随随便便成功!