15.1.2三角形的三边关系课件

(共14张PPT)
磐石办回民中学：刘效华
15.1.2 三角形的三边关系
1、通过实验与探究，发现三角形三边之间的关系；
2、会判断长度已知的三条线段能否组成三角形；
3、通过实践操作活动，发展学生的推理能力和创新精神。
学习目标
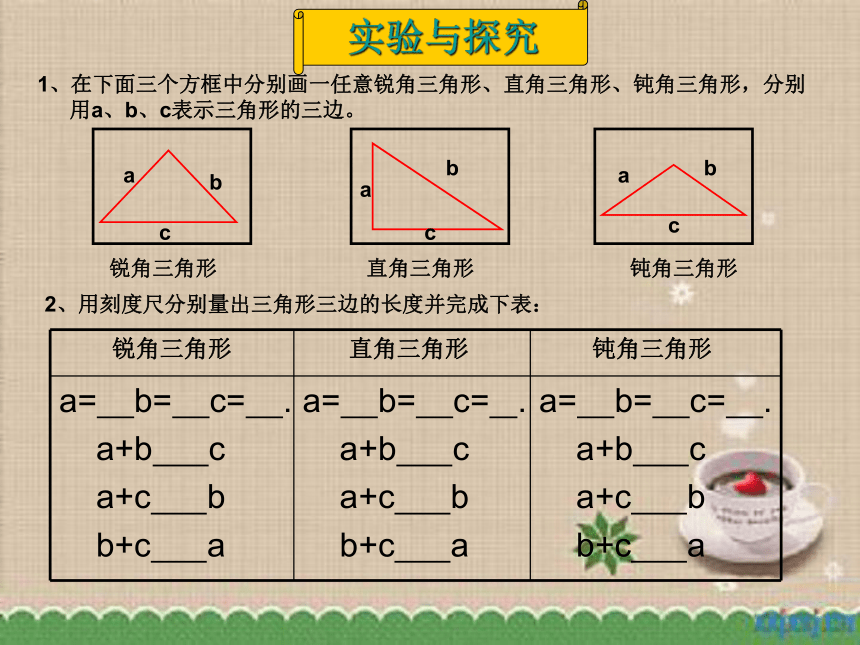
1、在下面三个方框中分别画一任意锐角三角形、直角三角形、钝角三角形，分别用a、b、c表示三角形的三边。
锐角三角形 直角三角形 钝角三角形
2、用刻度尺分别量出三角形三边的长度并完成下表：
锐角三角形 直角三角形 钝角三角形
a= b= c= .
a+b c
a+c b
b+c a a= b= c= .
a+b c
a+c b
b+c a a= b= c= .
a+b c
a+c b
b+c a
实验与探究
1、在下面三个方框中分别画一任意锐角三角形、直角三角形、钝角三角形，分别用a、b、c表示三角形的三边。
锐角三角形 直角三角形 钝角三角形
2、用刻度尺分别量出三角形三边的长度并完成下表：
锐角三角形 直角三角形 钝角三角形
a= b= c= .
a+b c
a+c b
b+c a a= b= c= .
a+b c
a+c b
b+c a a= b= c= .
a+b c
a+c b
b+c a
a
b
c
a
a
b
b
c
实验与探究
c
3、思考：
三角形中任意两边长度的和与第三边的长度之间有什么关系
三角形中任意两边的和大于第三边
4、你能利用学过的知识解释这一结论吗？
两点之间，线段最短。
例1 分别用下列长度的三条线段作为边长，能组成三角形吗？为什么？
（1）4，6，10； （2）5，6，7.
解：（1）因为4+6=10
所以，这三条线段不能组成三角形；
（2）长度分别为5,6的线段是这三条线段中
两条较短的线段。
因为5+6>7，
所以，这三条线段能组成三角形。
例题解析
只要用其中两条较短线段长度的和与第三条线段比较即可
跟踪练习
分别用下列长度的各组线段能组成三角形吗？
（1）3, 4, 5; （2）4, 4, 8； （3）4, 9, 9；
（4）5, 7, 11；（5）2, 3, 6.
解：（1）（3）（4）能
（2）（5）不能
例题解析
例2 等腰三角形的周长为21厘米，如果它的一边长
为5厘米，求其它两边的长。
解： 因为长为5厘米的边可能是等腰三角形的腰，也可能是 它的底边，所以应分两种情况进行讨论。
（1）如果底边长为5厘米，设腰长为x厘米，那么有
5+2x=21， 于是x=8；
（2）如果腰长为5厘米，设底边长为x厘米，那么有
2×5+x=21, 于是x=11;
但5+5<11,所以这种情况不能组成三角形。
由上可知，这个三角形其它两边的长都是8厘米。
跟踪练习
已知等腰三角形的周长为20。
（1）如果腰长为7，那么底边长是多少？
（2）如果底边长为7，那么腰长为多少？
（3）如果有一边长为4，那么另外两边的长
分别是多少？
解：
（1）腰长为7，设底边长为x，那么有
7+7+x=20 x=6 所以底边长为6。
（2）底边为7，设腰长为x，那么有
7+2x=20 x=6.5 所以腰长为6.5。
（3）因为4可能是腰，也可能是底边，所以分两种情况讨论
①如果底边为4，设腰长为x，那么有
4+2x=20 x=8 所以另外两边的长都是8。
②如果腰长为4，设底边为x，那么有
4+4+x=20 x=12
因为4+4=8 8＜12 所以这种情况不能组成三角形。
巩固练习
1、以下列各组线段为边，能组成三角形的是（ ）。
A 2cm 3cm 5cm B 3cm 3cm 6cm
C 5cm 8cm 2cm D 4cm 5cm 6cm
2、现有2cm、4cm、5cm、8cm长的4根木棒，任意选取3根组成一个三角形，可以组成不同三角形的个数为（ ）。
A 1个 B 2个 C 3个 D 4个
3、已知等腰三角形的两条边长分别为2和5，则它的周长为（ ）。
A 9 B 12 C 9或12 D 5
D
B
B
巩固练习
4、一个三角形的两边分别是3和8，第三边的长是一个奇数，则第三边的长可以是（ ）。
A 5或7 B 9 C 7 D 7或9
5、已知一个三角形的周长为15cm，且其中两边都等于第三边的2倍，那么这个三角形最短边为（ ）。
A 1cm B 2cm C 3cm D 4cm
D
C
课堂小结
你能谈一下本节课的收获吗？
作 业
一个三角形的其中两边长分别为3和9，且周长为偶数，求这个三角形第三边的长。