1.2.2同角三角函数的基本关系(第一课时)导学案
文档属性
| 名称 | 1.2.2同角三角函数的基本关系(第一课时)导学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 77.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-08 21:45:34 | ||
图片预览


文档简介
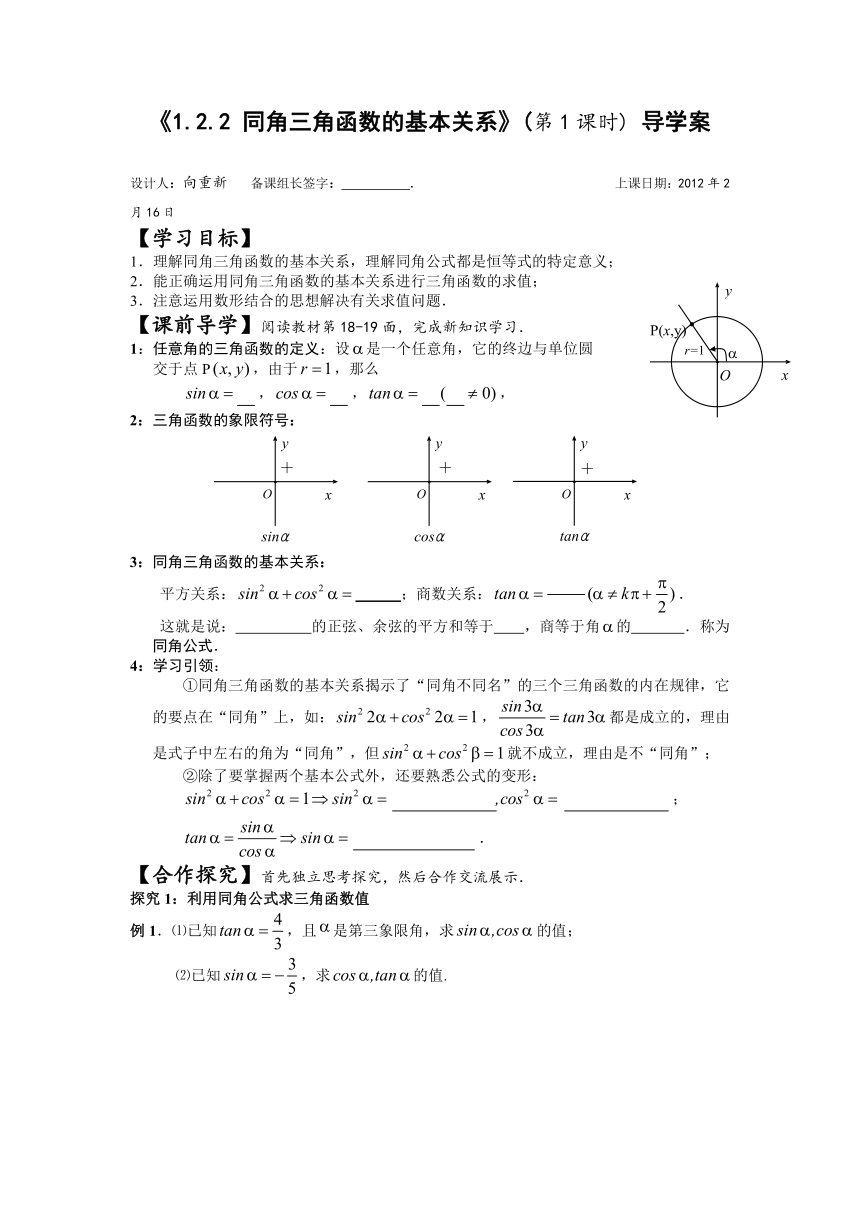
《1.2.2 同角三角函数的基本关系》(第1课时) 导学案
设计人:向重新 备课组长签字: . 上课日期:2012年2月16日
【学习目标】
1.理解同角三角函数的基本关系,理解同角公式都是恒等式的特定意义;
2.能正确运用同角三角函数的基本关系进行三角函数的求值;
3.注意运用数形结合的思想解决有关求值问题.
【课前导学】阅读教材第18-19面,完成新知识学习.
1:任意角的三角函数的定义:设是一个任意角,它的终边与单位圆
交于点P,由于,那么
,,,
2:三角函数的象限符号:
3:同角三角函数的基本关系:
平方关系: ;商数关系:.
这就是说: 的正弦、余弦的平方和等于 ,商等于角的 .称为同角公式.
4:学习引领:
①同角三角函数的基本关系揭示了“同角不同名”的三个三角函数的内在规律,它的要点在“同角”上,如:,都是成立的,理由是式子中左右的角为“同角”,但就不成立,理由是不“同角”;
②除了要掌握两个基本公式外,还要熟悉公式的变形:
;
.
【合作探究】首先独立思考探究,然后合作交流展示.
探究1:利用同角公式求三角函数值
例1.⑴已知,且是第三象限角,求的值;
⑵已知,求的值.
小结:使用平方关系求值,开方必须依据角所在的象限判断取正或负号,如果不确定就应该讨论.
例2.已知,求下列各式的值: ⑴;⑵.
小结:①如果一个式子的每一项都是关于的式子,且它们的次数之和相等,则称这个式子是关于的“齐次式”.“齐次化切”是一种重要的三角变形技巧.
②也是一种重要的三角变形技巧,称为“1的代换”.
探究2:运用平方关系化简三角函数式
例3.化简:⑴; ⑵
小结:“见根号,想平方”是一种常用的思路,,去掉绝对值符号,还是要看角所在的象限.
【基础检测】当堂达标练习,(时量:5分钟 满分:10分)计分:
1.已知,且角α是第二象限角,则( ).
A. 有 B. C. D.
2.已知(),则 ( )
A. B. C. D.
3.已知角θ是第三象限角,则可化简为( ).
A. B. C. D.
4. 已知,且,则 .
5. 已知,那么值是 .
【小组的表现】
优秀的小组: , 良好的小组: .
【自我评价】你完成本节导学案的情况为( )
A.很好 B.较好 C.一般 D.较差
班级 姓名 评价 .
【课堂小结】
1.同角三角函数的基本关系;2.同角三角函数基本关系的简单应用.
【能力提升】供学生课外做作业
1. 下列四个命题,可能成立的是( )
A.且 B.且
C.且 D.且
2. 已知,则( )
A. B. C. D.
3. 已知,则m=( )
A. 0 B. 8 C. 0或8 D. 不确定
4. 若是第二象限角,则下列式子成立的是 ( ).
A. B.
C. D.
5. 化简= .
6. 若,且,求的值.
7. 已知,求下列各式的值:⑴;⑵.?
8. (能力提高题) 若,化简.
r=1
P(x,y)
x
y
O
x
y
O
+
sinα
x
y
O
cosα
x
y
O
tanα
+
+
设计人:向重新 备课组长签字: . 上课日期:2012年2月16日
【学习目标】
1.理解同角三角函数的基本关系,理解同角公式都是恒等式的特定意义;
2.能正确运用同角三角函数的基本关系进行三角函数的求值;
3.注意运用数形结合的思想解决有关求值问题.
【课前导学】阅读教材第18-19面,完成新知识学习.
1:任意角的三角函数的定义:设是一个任意角,它的终边与单位圆
交于点P,由于,那么
,,,
2:三角函数的象限符号:
3:同角三角函数的基本关系:
平方关系: ;商数关系:.
这就是说: 的正弦、余弦的平方和等于 ,商等于角的 .称为同角公式.
4:学习引领:
①同角三角函数的基本关系揭示了“同角不同名”的三个三角函数的内在规律,它的要点在“同角”上,如:,都是成立的,理由是式子中左右的角为“同角”,但就不成立,理由是不“同角”;
②除了要掌握两个基本公式外,还要熟悉公式的变形:
;
.
【合作探究】首先独立思考探究,然后合作交流展示.
探究1:利用同角公式求三角函数值
例1.⑴已知,且是第三象限角,求的值;
⑵已知,求的值.
小结:使用平方关系求值,开方必须依据角所在的象限判断取正或负号,如果不确定就应该讨论.
例2.已知,求下列各式的值: ⑴;⑵.
小结:①如果一个式子的每一项都是关于的式子,且它们的次数之和相等,则称这个式子是关于的“齐次式”.“齐次化切”是一种重要的三角变形技巧.
②也是一种重要的三角变形技巧,称为“1的代换”.
探究2:运用平方关系化简三角函数式
例3.化简:⑴; ⑵
小结:“见根号,想平方”是一种常用的思路,,去掉绝对值符号,还是要看角所在的象限.
【基础检测】当堂达标练习,(时量:5分钟 满分:10分)计分:
1.已知,且角α是第二象限角,则( ).
A. 有 B. C. D.
2.已知(),则 ( )
A. B. C. D.
3.已知角θ是第三象限角,则可化简为( ).
A. B. C. D.
4. 已知,且,则 .
5. 已知,那么值是 .
【小组的表现】
优秀的小组: , 良好的小组: .
【自我评价】你完成本节导学案的情况为( )
A.很好 B.较好 C.一般 D.较差
班级 姓名 评价 .
【课堂小结】
1.同角三角函数的基本关系;2.同角三角函数基本关系的简单应用.
【能力提升】供学生课外做作业
1. 下列四个命题,可能成立的是( )
A.且 B.且
C.且 D.且
2. 已知,则( )
A. B. C. D.
3. 已知,则m=( )
A. 0 B. 8 C. 0或8 D. 不确定
4. 若是第二象限角,则下列式子成立的是 ( ).
A. B.
C. D.
5. 化简= .
6. 若,且,求的值.
7. 已知,求下列各式的值:⑴;⑵.?
8. (能力提高题) 若,化简.
r=1
P(x,y)
x
y
O
x
y
O
+
sinα
x
y
O
cosα
x
y
O
tanα
+
+
