山东省文登市七里汤中学2012届《方差》课件(人教版九年级下)13张
文档属性
| 名称 | 山东省文登市七里汤中学2012届《方差》课件(人教版九年级下)13张 |  | |
| 格式 | zip | ||
| 文件大小 | 188.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-08 21:54:13 | ||
图片预览





文档简介
(共13张PPT)
教
学
目
标 知识技能 理解方差的意义,会用方差公式求样本数据的方差
过程与方法 通过对实际问题的探究,形成方差的概念
情感态度价值观 以积极情感态度,探索问题,进而体会数学应用的科学价值
重点 方差概念形成过程
难点 方差概念形成过程
极差可以反映数据的波动范围,除此之外,统计中还常采用考察一组数据与它的平均数之间的差别的方法,来反映这组数据的波动情况.
讨
论
在一次女子排球比赛中,甲、乙两队来参赛选手的年龄如下:
甲队 26 25 28 28 24 28 26 28 27 29
乙队 28 27 25 28 27 26 28 27 27 26
(1)两队参赛选手的平均年龄分别是多少?
(2)你能说说两队参赛选手年龄波动的情况吗?
上面两组数据的平均数分别是
即甲、乙两队参赛选手的平均年龄相同
用图表整理这两组数据,分析你画出的图表,看看你能得出哪些结论?
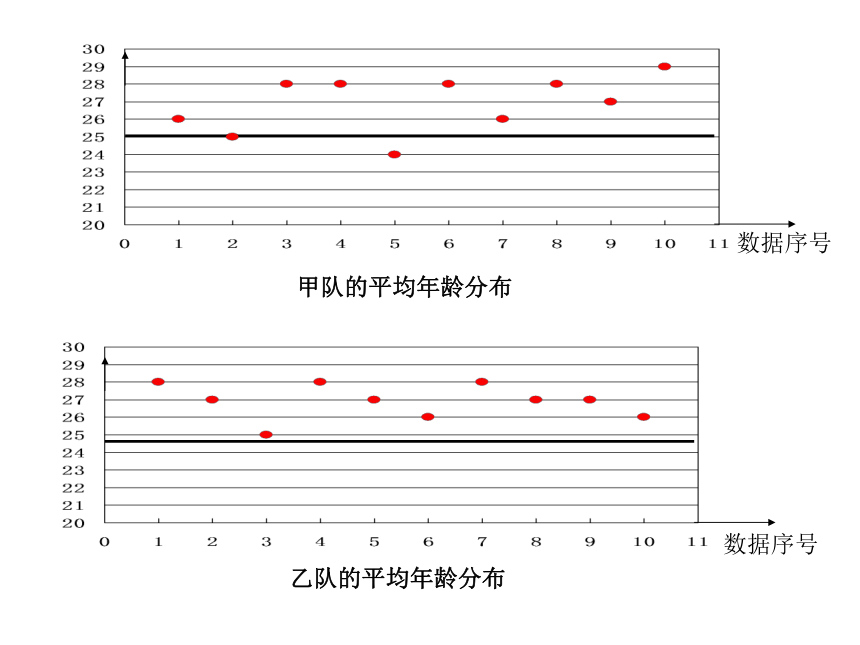
甲队的平均年龄分布
乙队的平均年龄分布
数据序号
数据序号
比较上面的两幅图可以看出,甲队选手的年龄与其平均年龄的偏差巨大,乙队选手的年龄较集中地分布在平均年龄左右,那么我们从图中看出的结果能否用一个量来刻画呢?
为了刻画一组数据的波动大小,可以采用很多方法,统计中常采用下面的做法:
方差越大,数据的波动越大;方差越小,数据的波动就越小
设有n 个数据x1,x2,…,xn ,各数据与它们的平均数的差的平方分别是 ,我们用它们的平均数,即用
来衡量这组数据的波动大小,并把它叫做这组数据的方差(variance),记作s2
两组数据的方差分别是:
显然 ,由此可知甲队选手年龄的波动较大,这与我们从图看到的结果 是一致的.
例1 在一次芭蕾舞的比赛中,甲乙两个芭蕾舞团都表演了舞剧(天鹅湖),参加表演的女演员的身高(单位:cm)分别是
甲团 163 164 164 165 165 165 166 167
乙团 163 164 164 165 166 167 167 168
哪个芭蕾舞团的女演员的身高更整齐?
解: 甲乙两团演员的身高更分别是:
由
可知甲芭蕾舞团女演员的身高更整齐.
练习
1、用条型图表示下列各组数据,计算并比较它们的平均数和方差,体会方差是怎样刻画数据的波动程度的.
(1)6 6 6 6 6 6 6
(2)5 5 6 6 6 7 7
(3)3 3 4 6 8 9 9
(4)3 3 3 6 9 9 9
2、下面是两名跳远运动员的10次测验成绩(单位:m)
甲 5.85 5.93 6.07 5.91 5.99
6.13 5.98 6.05 6.00 6.19
乙 6.11 6.08 5.83 5.92 5.84
5.81 6.18 6.17 5.85 6.21
在这10次测验中,哪名运动员的成绩更稳定?(可以使用计算器)
1. 本 节 主 要 知 识 内容
方差越大,数据的波动越大;方差越小,数据的波动就越小
设有n 个数据x1,x2,…,xn ,各数据与它们的平均数的差的平方分别是 ,我们用它们的平均数,即用
来衡量这组数据的波动大小,并把它叫做这组数据的方差(variance),记作s2
教
学
目
标 知识技能 理解方差的意义,会用方差公式求样本数据的方差
过程与方法 通过对实际问题的探究,形成方差的概念
情感态度价值观 以积极情感态度,探索问题,进而体会数学应用的科学价值
重点 方差概念形成过程
难点 方差概念形成过程
极差可以反映数据的波动范围,除此之外,统计中还常采用考察一组数据与它的平均数之间的差别的方法,来反映这组数据的波动情况.
讨
论
在一次女子排球比赛中,甲、乙两队来参赛选手的年龄如下:
甲队 26 25 28 28 24 28 26 28 27 29
乙队 28 27 25 28 27 26 28 27 27 26
(1)两队参赛选手的平均年龄分别是多少?
(2)你能说说两队参赛选手年龄波动的情况吗?
上面两组数据的平均数分别是
即甲、乙两队参赛选手的平均年龄相同
用图表整理这两组数据,分析你画出的图表,看看你能得出哪些结论?
甲队的平均年龄分布
乙队的平均年龄分布
数据序号
数据序号
比较上面的两幅图可以看出,甲队选手的年龄与其平均年龄的偏差巨大,乙队选手的年龄较集中地分布在平均年龄左右,那么我们从图中看出的结果能否用一个量来刻画呢?
为了刻画一组数据的波动大小,可以采用很多方法,统计中常采用下面的做法:
方差越大,数据的波动越大;方差越小,数据的波动就越小
设有n 个数据x1,x2,…,xn ,各数据与它们的平均数的差的平方分别是 ,我们用它们的平均数,即用
来衡量这组数据的波动大小,并把它叫做这组数据的方差(variance),记作s2
两组数据的方差分别是:
显然 ,由此可知甲队选手年龄的波动较大,这与我们从图看到的结果 是一致的.
例1 在一次芭蕾舞的比赛中,甲乙两个芭蕾舞团都表演了舞剧(天鹅湖),参加表演的女演员的身高(单位:cm)分别是
甲团 163 164 164 165 165 165 166 167
乙团 163 164 164 165 166 167 167 168
哪个芭蕾舞团的女演员的身高更整齐?
解: 甲乙两团演员的身高更分别是:
由
可知甲芭蕾舞团女演员的身高更整齐.
练习
1、用条型图表示下列各组数据,计算并比较它们的平均数和方差,体会方差是怎样刻画数据的波动程度的.
(1)6 6 6 6 6 6 6
(2)5 5 6 6 6 7 7
(3)3 3 4 6 8 9 9
(4)3 3 3 6 9 9 9
2、下面是两名跳远运动员的10次测验成绩(单位:m)
甲 5.85 5.93 6.07 5.91 5.99
6.13 5.98 6.05 6.00 6.19
乙 6.11 6.08 5.83 5.92 5.84
5.81 6.18 6.17 5.85 6.21
在这10次测验中,哪名运动员的成绩更稳定?(可以使用计算器)
1. 本 节 主 要 知 识 内容
方差越大,数据的波动越大;方差越小,数据的波动就越小
设有n 个数据x1,x2,…,xn ,各数据与它们的平均数的差的平方分别是 ,我们用它们的平均数,即用
来衡量这组数据的波动大小,并把它叫做这组数据的方差(variance),记作s2
同课章节目录
