定积分与微积分基本定理教案
图片预览


文档简介
课题 1.4.1 曲边梯形面积与定积分 授课日期 年 月 日
第 课时
三维目标(体现高考考点的落实) 知识与技能 通过探求曲边梯形的面积,使学生了解定积分的实际背景,了解“以直代曲”“逼近”的思想方法,建立微积分的概念的认识基础
过程与方法 了解曲边梯形面积与变速直线运动的共同特征
情感、态度、价值观 通过探求曲边梯形的面积,使学生了解定积分的实际背景,了解“以直代曲”“逼近”的思想方法,建立微积分的概念的认识基础
教学重点 了解定积分的基本思想“以直代曲” “逼近”的思想
教学难点 “以直代曲” “逼近”的思想的形成求和符号
授课类型 新授课
教学设计(包括以下内容:①预习 ②设置问题、回答问题 ③合作探究 ④课堂训练)
共案设计(经集体讨论形成) 个案设计
教师活动 学生活动 (根据个人教学风格和学生特点形成)
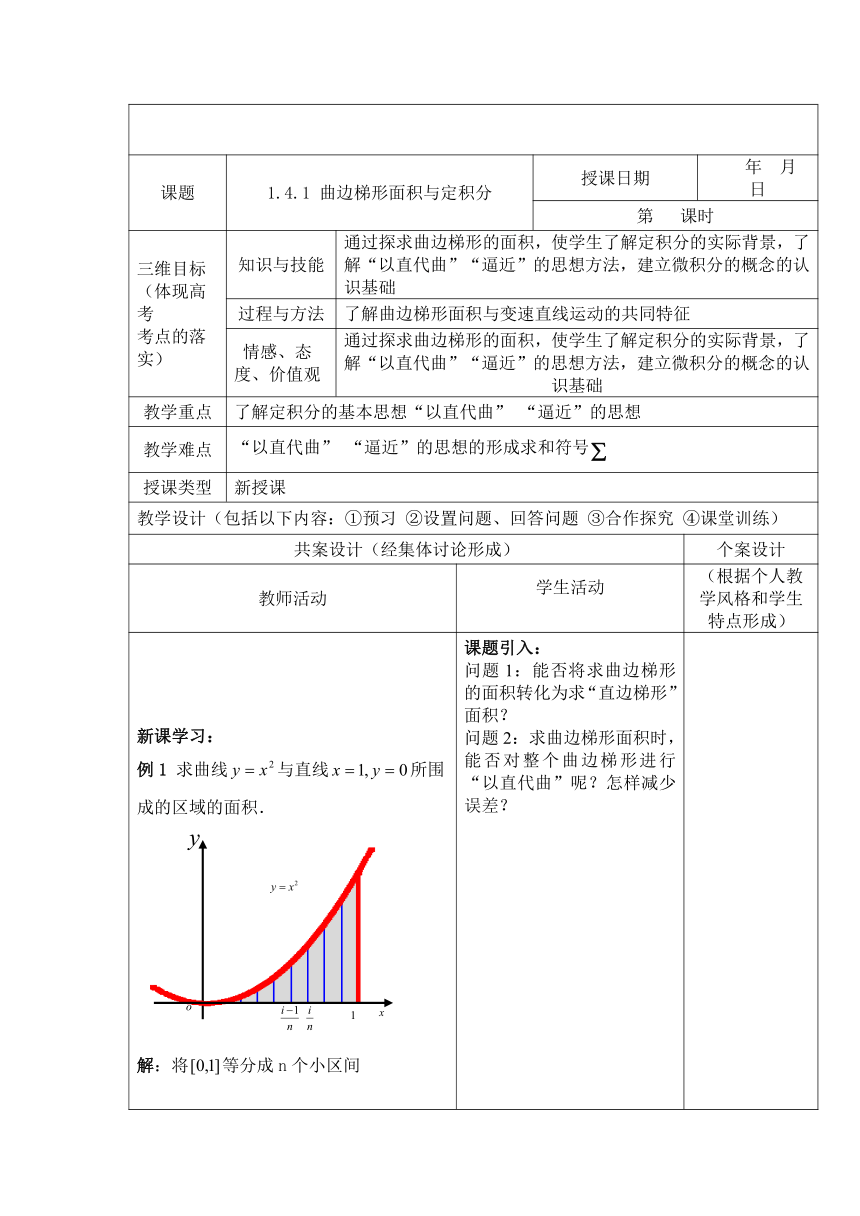
新课学习:例1 求曲线与直线所围成的区域的面积.解:将等分成n个小区间,区间的长度为,区间左端点的纵坐标为高,曲线下方矩形面积为所以 例2 弹簧在拉伸过程中,力与伸长量成正比,即力(是常数,是伸长量).求弹簧从平衡位置拉长所做的功.解定积分的定义设函数定义在区间上,用分点把区间分为n个小区间,其长度依次为,记为这些区间长度的最大者,当趋向于0时,所有的小区间长度都趋向于0,每个小区间内任取一点,作和式当时,如果和式的极限存在,我们把和式的极限叫作函数在区间上的定积分,记作叫作被积函数,a叫积分下限,b叫积分上限,叫被积式由定积分的定义,可得到如下性质 课题引入:问题1:能否将求曲边梯形的面积转化为求“直边梯形”面积?问题2:求曲边梯形面积时,能否对整个曲边梯形进行“以直代曲”呢?怎样减少误差?3+1教学建议当取左端点是矩形面积之和小于曲边梯形面积,当取右端点时会怎样?尝试着去计算3+1教学建议完成课后练习B,求曲边梯形的面积
课堂小结 求定积分的步骤:1 分割2 取点3 求和4 取极限
板书设计
教学反思
教研组长评价 共案: 个案: 等级: 签字: 时间:
课题 1.4.2 微积分基本定理 授课日期 年 月 日
第 课时
三维目标(体现高考考点的落实) 知识与技能 通过实例,直观了解微积分基本定理的含义,会用牛顿-莱布尼兹公式求简单的定积分
过程与方法 通过实例体会用微积分基本定理求定积分的方法
情感、态度、价值观 通过微积分基本定理的学习,体会事物间的相互转化、对立统一的辩证关系,培养学生辩证唯物主义观点,提高理性思维能力
教学重点 通过探究变速直线运动物体的速度与位移的关系,使学生直观了解微积分基本定理的含义,并能正确运用基本定理计算简单的定积分
教学难点 了解微积分基本定理的含义
授课类型 新授课
教学设计(包括以下内容:①预习 ②设置问题、回答问题 ③合作探究 ④课堂训练)
共案设计(经集体讨论形成) 个案设计
教师活动 学生活动 (根据个人教学风格和学生特点形成)
引人新课:我们讲过用定积分定义计算定积分,但其计算过程比较复杂,所以不是求定积分的一般方法。我们必须寻求计算定积分的新方法,也是比较一般的方法新课学习:对于一般函数,设,有 我们找到了用的原函数(即满足)的数值差来计算在上的定积分的方法。注:1:定理 如果函数是上的连续函数的任意一个原函数,则为了方便起见,还常用表示,即 该式称之为微积分基本公式或牛顿—莱布尼兹公式。它指出了求连续函数定积分的一般方法,把求定积分的问题,转化成求原函数的问题,是微分学与积分学之间联系的桥梁。 它不仅揭示了导数和定积分之间的内在联系,同时也提供计算定积分的一种有效方法,为后面的学习奠定了基础。因此它在教材中处于极其重要的地位,起到了承上启下的作用,不仅如此,它甚至给微积分学的发展带来了深远的影响,是微积分学中最重要最辉煌的成果。例题讲解例1 求在上阴影部分的面积S解:因为, 所以例2 求曲线与轴在区间上所围成阴影部分的面积S解:例3 计算:(1);(2)解: 3+1教学建议学生自学微积分基本定理的推导过程3+1教学建议学生自主完成课后练习A
课堂小结 本节课借助于变速运动物体的速度与路程的关系以及图形得出了特殊情况下的牛顿-莱布尼兹公式.成立,进而推广到了一般的函数,得出了微积分基本定理,得到了一种求定积分的简便方法,运用这种方法的关键是找到被积函数的原函数,这就要求大家前面的求导数的知识比较熟练,希望,不明白的同学,回头来多复习!
板书设计
教学反思
教研组长评价 共案: 个案: 等级: 签字: 时间:
第 课时
三维目标(体现高考考点的落实) 知识与技能 通过探求曲边梯形的面积,使学生了解定积分的实际背景,了解“以直代曲”“逼近”的思想方法,建立微积分的概念的认识基础
过程与方法 了解曲边梯形面积与变速直线运动的共同特征
情感、态度、价值观 通过探求曲边梯形的面积,使学生了解定积分的实际背景,了解“以直代曲”“逼近”的思想方法,建立微积分的概念的认识基础
教学重点 了解定积分的基本思想“以直代曲” “逼近”的思想
教学难点 “以直代曲” “逼近”的思想的形成求和符号
授课类型 新授课
教学设计(包括以下内容:①预习 ②设置问题、回答问题 ③合作探究 ④课堂训练)
共案设计(经集体讨论形成) 个案设计
教师活动 学生活动 (根据个人教学风格和学生特点形成)
新课学习:例1 求曲线与直线所围成的区域的面积.解:将等分成n个小区间,区间的长度为,区间左端点的纵坐标为高,曲线下方矩形面积为所以 例2 弹簧在拉伸过程中,力与伸长量成正比,即力(是常数,是伸长量).求弹簧从平衡位置拉长所做的功.解定积分的定义设函数定义在区间上,用分点把区间分为n个小区间,其长度依次为,记为这些区间长度的最大者,当趋向于0时,所有的小区间长度都趋向于0,每个小区间内任取一点,作和式当时,如果和式的极限存在,我们把和式的极限叫作函数在区间上的定积分,记作叫作被积函数,a叫积分下限,b叫积分上限,叫被积式由定积分的定义,可得到如下性质 课题引入:问题1:能否将求曲边梯形的面积转化为求“直边梯形”面积?问题2:求曲边梯形面积时,能否对整个曲边梯形进行“以直代曲”呢?怎样减少误差?3+1教学建议当取左端点是矩形面积之和小于曲边梯形面积,当取右端点时会怎样?尝试着去计算3+1教学建议完成课后练习B,求曲边梯形的面积
课堂小结 求定积分的步骤:1 分割2 取点3 求和4 取极限
板书设计
教学反思
教研组长评价 共案: 个案: 等级: 签字: 时间:
课题 1.4.2 微积分基本定理 授课日期 年 月 日
第 课时
三维目标(体现高考考点的落实) 知识与技能 通过实例,直观了解微积分基本定理的含义,会用牛顿-莱布尼兹公式求简单的定积分
过程与方法 通过实例体会用微积分基本定理求定积分的方法
情感、态度、价值观 通过微积分基本定理的学习,体会事物间的相互转化、对立统一的辩证关系,培养学生辩证唯物主义观点,提高理性思维能力
教学重点 通过探究变速直线运动物体的速度与位移的关系,使学生直观了解微积分基本定理的含义,并能正确运用基本定理计算简单的定积分
教学难点 了解微积分基本定理的含义
授课类型 新授课
教学设计(包括以下内容:①预习 ②设置问题、回答问题 ③合作探究 ④课堂训练)
共案设计(经集体讨论形成) 个案设计
教师活动 学生活动 (根据个人教学风格和学生特点形成)
引人新课:我们讲过用定积分定义计算定积分,但其计算过程比较复杂,所以不是求定积分的一般方法。我们必须寻求计算定积分的新方法,也是比较一般的方法新课学习:对于一般函数,设,有 我们找到了用的原函数(即满足)的数值差来计算在上的定积分的方法。注:1:定理 如果函数是上的连续函数的任意一个原函数,则为了方便起见,还常用表示,即 该式称之为微积分基本公式或牛顿—莱布尼兹公式。它指出了求连续函数定积分的一般方法,把求定积分的问题,转化成求原函数的问题,是微分学与积分学之间联系的桥梁。 它不仅揭示了导数和定积分之间的内在联系,同时也提供计算定积分的一种有效方法,为后面的学习奠定了基础。因此它在教材中处于极其重要的地位,起到了承上启下的作用,不仅如此,它甚至给微积分学的发展带来了深远的影响,是微积分学中最重要最辉煌的成果。例题讲解例1 求在上阴影部分的面积S解:因为, 所以例2 求曲线与轴在区间上所围成阴影部分的面积S解:例3 计算:(1);(2)解: 3+1教学建议学生自学微积分基本定理的推导过程3+1教学建议学生自主完成课后练习A
课堂小结 本节课借助于变速运动物体的速度与路程的关系以及图形得出了特殊情况下的牛顿-莱布尼兹公式.成立,进而推广到了一般的函数,得出了微积分基本定理,得到了一种求定积分的简便方法,运用这种方法的关键是找到被积函数的原函数,这就要求大家前面的求导数的知识比较熟练,希望,不明白的同学,回头来多复习!
板书设计
教学反思
教研组长评价 共案: 个案: 等级: 签字: 时间:
