两个计数原理
图片预览








文档简介
(共23张PPT)
分类加法计数原理
与
分步乘法计数原理
某敌国计划对我国军事重地发射导弹袭击。启动导弹要输入由数字或者英文字母组成的10位密码。为了粉碎敌人的阴谋,某战士反复尝试输入字符,希望碰运气破解密码,那么可能最多要尝试多少次?
观察1:假设从广州到上海去,有两类交通工具可以选择:省钱类的是乘火车,奢侈类的是乘飞机。火车有3班,飞机有5班.那么,你从广州到上海共有多少种不同的走法?
观察2:报考大学填志愿时第一志愿很重要,要考虑清楚填那所大学。假设医学类的有5所大学可以选择,经济类有10所,理学类的有15所,工学类的有23所。你若任意从中选一所填写,那么有多少种填法?
答:共有 N= 3+5 = 8 种走法。
答:共有 N= 5+10+15+23 = 53 种填法。
观察3::在填写高考志愿表时,一名高中毕业生了解到,A,B两所大学各有一些自己感兴趣的专业,具体全部罗列如下:
A大学 B大学 C大学
生物学 应用数学 新闻学
化学 会计学 金融学
医学 信息技术学 人力资源学
法学 物理学
那么,这名同学可能的专业选择共有多少个?
答:共有 N= 4+4 +3= 11 种专业选择。
做一件事,完成它可以有n类办法,在第一类办法中有m1种不同的方法 ,在第二类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法,那么完成这件事共有:
——————————————
种不同的办法。
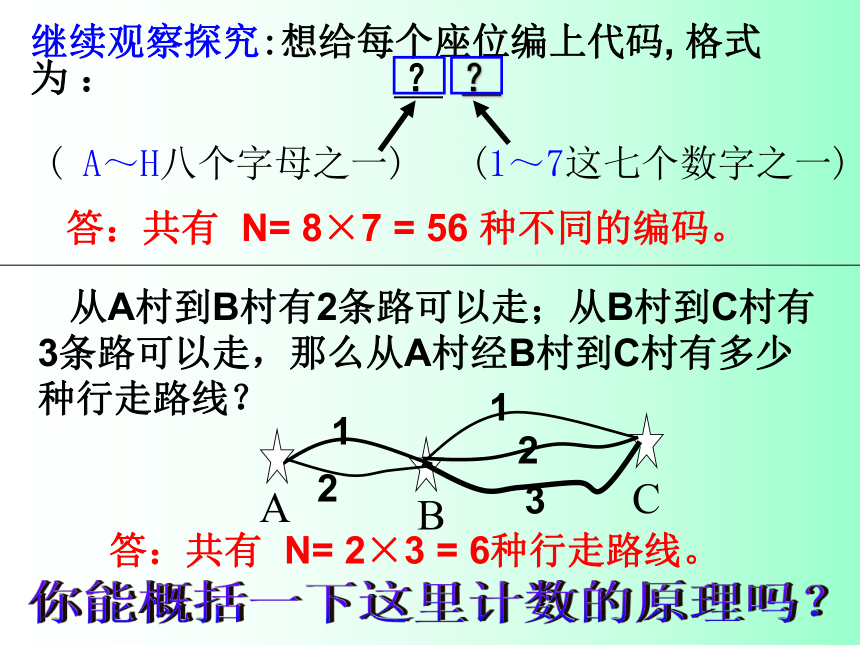
继续观察探究:想给每个座位编上代码, 格式为 : ? ?
从A村到B村有2条路可以走;从B村到C村有3条路可以走,那么从A村经B村到C村有多少种行走路线?
答:共有 N= 8×7 = 56 种不同的编码。
答:共有 N= 2×3 = 6种行走路线。
( A~H八个字母之一)
(1~7这七个数字之一)
A
B
C
1
2
1
2
3
做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同方法,那么完成这件事共有
———————————————— 种不同的方法。
逐步完成上述两步,才完成整件事,所以依据____________原理,
1 .某班有男生30名,女生24名. 现要从中选出男、女生各一名代表班级参加比赛,共有多少种不同的选法?
解:要 “选出2名代表”,
20.再选一名女生,有24种选法;
完成这件事,共有30×24=720种不同的方法。
分步乘法
完成它需分两个步骤:
10.先选一名男生,有30种选法;
1: 书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放2本不同的体育书.
①从书架上任取1本书,有多少种不同的取法?
②从书架的第1、2、3层各取1本书,有多少种不同的取法?
③从书架上任取两本不同学科的书,有多少种不同的取法?
熟悉原理的练习:
N=4+3+2=9种不同取法。
解.取1本书,
解.取三本书,有:
4×3
3×2
2×4
N=4×3×2=24种不同取法。
N= + + = 26种取法
解.取2本书,有:
依加法原理有:
小结:何时运用加法原理?何时运用乘法原理?
做一件事,有好几类办法,要分类讨论的时候,运用加法原理 ;
做一件事,需要分解步骤、逐步地做,直到最后一步做完才算完成,就运用乘法原理 ;
2. 如图电路图,
从A到B共有
条不同的线路
可通电。
A
B
8
再练一个:
3
1
2×2
N= + + = 条不同线路。
8
分三大类
(一)排位问题
(在黑板书写)
例1.用1,,2,3,4,5,这五个数字中的数排列成一个四位数,各位上的数字可以重复,可以排出多少种不同的四位数?
(在黑板书写)
例2.用1,,2,3,4,5,这五个数字中的数排列成一个四位数,各位上的数字不重复。
可以排出多少种不同的4位数?
变问:若要求这个4位数是偶数,则有多少种?
变问:若要求这个4位数是奇数,则有多少种?
变问:若要求这个4位数大于2012,则有多少种?
练习:
某人给程序文件命名,需要用3个字符,其中首字符要求用字母 A~G 或 U~Z , 后两个要求用数字1~9.问最多可以给出多少个不同的文件名?
小结:何时运用加法原理?何时运用乘法原理?
做一件事,有好几类办法,要分类讨论的时候,运用加法原理 ;
做一件事,需要分解步骤、逐步地做,直到最后一步做完才算完成,就运用乘法原理 ;
课外作业:导学案两个基本原理(1)上的“巩固练习”和作业。
例1: 一个圆被分成3块扇形。现在用5种不同的颜色给3块扇形涂色,要求相邻扇形的颜色互不相同,问有多少钟不同的涂法?若分割成4块扇形呢?
(二)涂色问题
试举一反三:
若改为4块扇形呢?
练习: 要给①,②,③,④四块区域分别涂上一种颜色,有五种颜色可以备用,允许同一种颜色使用多次, 但相邻区域必须涂不同颜色,求不同涂色方法种数。
典型问题解析 (二)涂色问题
①
②
③
④
例6. 核糖核酸(RNA)分子是在生物细胞中发现的化学成分一个 RNA 分子是一个有着数百个甚至数千个位置的长链,长链中每一个位置上都由一种称为碱基的化学成分所占据.总共有 4 种不同的碱基,分别用A,C,G,U表示.在一个 RNA 分子中,各种碱基能够以任意次序出现,所以在任意一个位置上的碱基与其他位置上的碱基无关.假设有一类 RNA 分子由 100 个碱基组成,那么能有多少种不同的 RNA 分子?
典型问题解析 (一)排位问题
例7电子元件很容易实现电路的通与断、电位的高与低等两种状态,而这也是最容易控制的两种状态.因此计算机内部就采用了每一位只有 O 或 1 两种数字的记数法,即二进制.为了使计算机能够识别字符,需要对字符进行编码,每个字符可以用一个或多个字节来表示,每个字节由 8 个二进制位构成.问:
(1)一个字节( 8 位)最多可以表示多少个不同的字符?
(2)计算机汉字国标码(GB 码)包含了6 763 个汉字,一个汉字为一个字符,要对这些汉字进行编码,每个汉字至少要用多少个字节表示?
典型问题解析 (一)排位问题
例9.随着人们生活水平的提高,某城市家庭汽车拥有量迅速增长,汽车牌照号码需交通管理部门出台了一种汽车牌照组成办法,每一个汽车牌照都必须有3个不重复的英文字母和 3 个不重复的阿拉伯数字,并且 3 个字母必须合成一组出现,3个数字也必须合成一组出现.那么这种办法共能给多少辆汽车上牌照?
典型问题解析 (一)排位问题
例2 某城在中心广场造一个花圃,花圃分为6个部分(如图).现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有 ________ 种.(以数字作答)
120
典型问题解析 (二)涂色问题
例1 从集合{1,2,3,3,……,10}中,选出 5个不同的数字组成子集,要求这5个数中的任何两个数的和不等于11,这样的子集共有多少个?
【评述】本题的关键是先找出和为11的5组数,然后利用分步计数原理求出结果。
(三)集合与映射问题
例2.(投宿问题)有3个人到一个小镇上旅游,晚上住宿有五家旅店可以选择。若他们各人可以随意选择住哪家旅店。
住宿有多少种不同的安排方法?
若这三人必须分散住在不同旅店,有多少种安排方法?若这三人必须住在同一家旅店呢?
例3: 集合A=
, B=
, f是从A 到
B的映射. (1) 从A到B总共有几个映射 (2)若B中
每个元素都有原象,则可建立几个不同的映射
(3)若B中的元素0没有原象,则这样的映射有几个
(5)若f 满足 则这样的f又有几个
(4)若B中有一个元素没有原象,则这样的映射有几个
注意:“分类”互斥且全面,
“分步”循序有条理。
分类加法计数原理
与
分步乘法计数原理
某敌国计划对我国军事重地发射导弹袭击。启动导弹要输入由数字或者英文字母组成的10位密码。为了粉碎敌人的阴谋,某战士反复尝试输入字符,希望碰运气破解密码,那么可能最多要尝试多少次?
观察1:假设从广州到上海去,有两类交通工具可以选择:省钱类的是乘火车,奢侈类的是乘飞机。火车有3班,飞机有5班.那么,你从广州到上海共有多少种不同的走法?
观察2:报考大学填志愿时第一志愿很重要,要考虑清楚填那所大学。假设医学类的有5所大学可以选择,经济类有10所,理学类的有15所,工学类的有23所。你若任意从中选一所填写,那么有多少种填法?
答:共有 N= 3+5 = 8 种走法。
答:共有 N= 5+10+15+23 = 53 种填法。
观察3::在填写高考志愿表时,一名高中毕业生了解到,A,B两所大学各有一些自己感兴趣的专业,具体全部罗列如下:
A大学 B大学 C大学
生物学 应用数学 新闻学
化学 会计学 金融学
医学 信息技术学 人力资源学
法学 物理学
那么,这名同学可能的专业选择共有多少个?
答:共有 N= 4+4 +3= 11 种专业选择。
做一件事,完成它可以有n类办法,在第一类办法中有m1种不同的方法 ,在第二类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法,那么完成这件事共有:
——————————————
种不同的办法。
继续观察探究:想给每个座位编上代码, 格式为 : ? ?
从A村到B村有2条路可以走;从B村到C村有3条路可以走,那么从A村经B村到C村有多少种行走路线?
答:共有 N= 8×7 = 56 种不同的编码。
答:共有 N= 2×3 = 6种行走路线。
( A~H八个字母之一)
(1~7这七个数字之一)
A
B
C
1
2
1
2
3
做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同方法,那么完成这件事共有
———————————————— 种不同的方法。
逐步完成上述两步,才完成整件事,所以依据____________原理,
1 .某班有男生30名,女生24名. 现要从中选出男、女生各一名代表班级参加比赛,共有多少种不同的选法?
解:要 “选出2名代表”,
20.再选一名女生,有24种选法;
完成这件事,共有30×24=720种不同的方法。
分步乘法
完成它需分两个步骤:
10.先选一名男生,有30种选法;
1: 书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放2本不同的体育书.
①从书架上任取1本书,有多少种不同的取法?
②从书架的第1、2、3层各取1本书,有多少种不同的取法?
③从书架上任取两本不同学科的书,有多少种不同的取法?
熟悉原理的练习:
N=4+3+2=9种不同取法。
解.取1本书,
解.取三本书,有:
4×3
3×2
2×4
N=4×3×2=24种不同取法。
N= + + = 26种取法
解.取2本书,有:
依加法原理有:
小结:何时运用加法原理?何时运用乘法原理?
做一件事,有好几类办法,要分类讨论的时候,运用加法原理 ;
做一件事,需要分解步骤、逐步地做,直到最后一步做完才算完成,就运用乘法原理 ;
2. 如图电路图,
从A到B共有
条不同的线路
可通电。
A
B
8
再练一个:
3
1
2×2
N= + + = 条不同线路。
8
分三大类
(一)排位问题
(在黑板书写)
例1.用1,,2,3,4,5,这五个数字中的数排列成一个四位数,各位上的数字可以重复,可以排出多少种不同的四位数?
(在黑板书写)
例2.用1,,2,3,4,5,这五个数字中的数排列成一个四位数,各位上的数字不重复。
可以排出多少种不同的4位数?
变问:若要求这个4位数是偶数,则有多少种?
变问:若要求这个4位数是奇数,则有多少种?
变问:若要求这个4位数大于2012,则有多少种?
练习:
某人给程序文件命名,需要用3个字符,其中首字符要求用字母 A~G 或 U~Z , 后两个要求用数字1~9.问最多可以给出多少个不同的文件名?
小结:何时运用加法原理?何时运用乘法原理?
做一件事,有好几类办法,要分类讨论的时候,运用加法原理 ;
做一件事,需要分解步骤、逐步地做,直到最后一步做完才算完成,就运用乘法原理 ;
课外作业:导学案两个基本原理(1)上的“巩固练习”和作业。
例1: 一个圆被分成3块扇形。现在用5种不同的颜色给3块扇形涂色,要求相邻扇形的颜色互不相同,问有多少钟不同的涂法?若分割成4块扇形呢?
(二)涂色问题
试举一反三:
若改为4块扇形呢?
练习: 要给①,②,③,④四块区域分别涂上一种颜色,有五种颜色可以备用,允许同一种颜色使用多次, 但相邻区域必须涂不同颜色,求不同涂色方法种数。
典型问题解析 (二)涂色问题
①
②
③
④
例6. 核糖核酸(RNA)分子是在生物细胞中发现的化学成分一个 RNA 分子是一个有着数百个甚至数千个位置的长链,长链中每一个位置上都由一种称为碱基的化学成分所占据.总共有 4 种不同的碱基,分别用A,C,G,U表示.在一个 RNA 分子中,各种碱基能够以任意次序出现,所以在任意一个位置上的碱基与其他位置上的碱基无关.假设有一类 RNA 分子由 100 个碱基组成,那么能有多少种不同的 RNA 分子?
典型问题解析 (一)排位问题
例7电子元件很容易实现电路的通与断、电位的高与低等两种状态,而这也是最容易控制的两种状态.因此计算机内部就采用了每一位只有 O 或 1 两种数字的记数法,即二进制.为了使计算机能够识别字符,需要对字符进行编码,每个字符可以用一个或多个字节来表示,每个字节由 8 个二进制位构成.问:
(1)一个字节( 8 位)最多可以表示多少个不同的字符?
(2)计算机汉字国标码(GB 码)包含了6 763 个汉字,一个汉字为一个字符,要对这些汉字进行编码,每个汉字至少要用多少个字节表示?
典型问题解析 (一)排位问题
例9.随着人们生活水平的提高,某城市家庭汽车拥有量迅速增长,汽车牌照号码需交通管理部门出台了一种汽车牌照组成办法,每一个汽车牌照都必须有3个不重复的英文字母和 3 个不重复的阿拉伯数字,并且 3 个字母必须合成一组出现,3个数字也必须合成一组出现.那么这种办法共能给多少辆汽车上牌照?
典型问题解析 (一)排位问题
例2 某城在中心广场造一个花圃,花圃分为6个部分(如图).现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有 ________ 种.(以数字作答)
120
典型问题解析 (二)涂色问题
例1 从集合{1,2,3,3,……,10}中,选出 5个不同的数字组成子集,要求这5个数中的任何两个数的和不等于11,这样的子集共有多少个?
【评述】本题的关键是先找出和为11的5组数,然后利用分步计数原理求出结果。
(三)集合与映射问题
例2.(投宿问题)有3个人到一个小镇上旅游,晚上住宿有五家旅店可以选择。若他们各人可以随意选择住哪家旅店。
住宿有多少种不同的安排方法?
若这三人必须分散住在不同旅店,有多少种安排方法?若这三人必须住在同一家旅店呢?
例3: 集合A=
, B=
, f是从A 到
B的映射. (1) 从A到B总共有几个映射 (2)若B中
每个元素都有原象,则可建立几个不同的映射
(3)若B中的元素0没有原象,则这样的映射有几个
(5)若f 满足 则这样的f又有几个
(4)若B中有一个元素没有原象,则这样的映射有几个
注意:“分类”互斥且全面,
“分步”循序有条理。
