抛物线及其标准方程
图片预览




文档简介
(共14张PPT)
抛物线
定义与标准方程
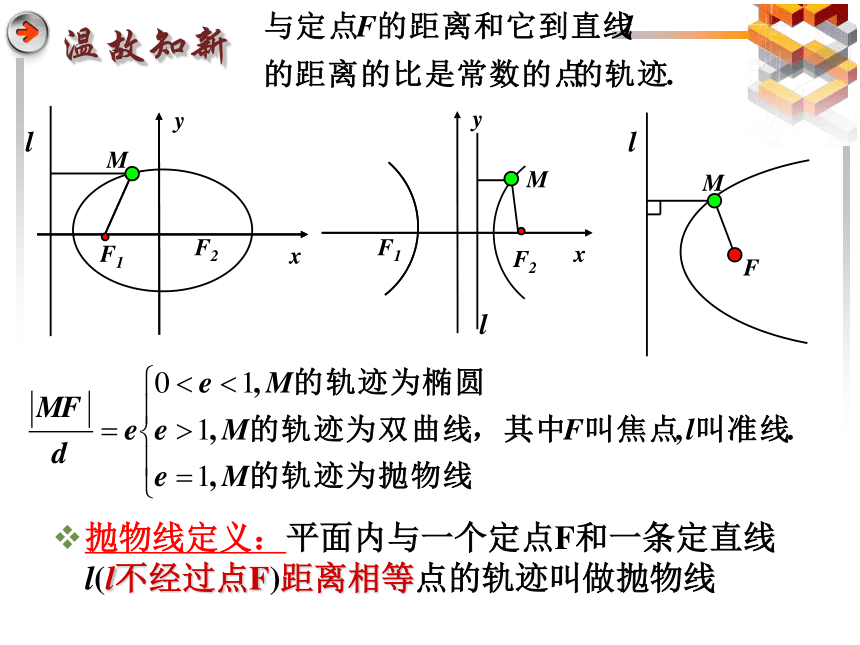
温故知新
抛物线定义:平面内与一个定点F和一条定直线l(l不经过点F)距离相等点的轨迹叫做抛物线
F1
F2
M
y
x
l
y
x
F1
F2
M
l
F
l
M
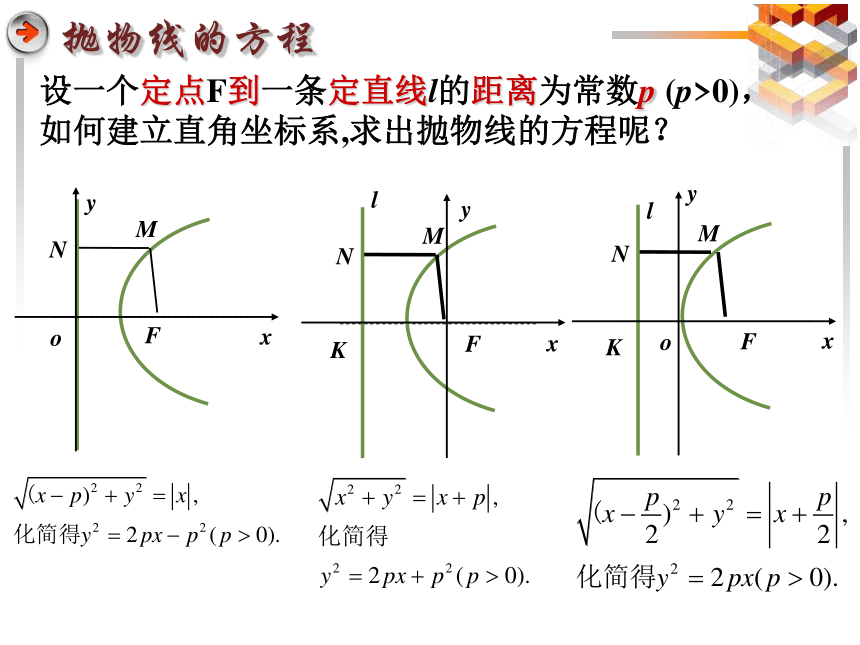
抛物线的方程
y
o
F
M
N
x
设一个定点F到一条定直线l的距离为常数p (p>0),
如何建立直角坐标系,求出抛物线的方程呢?
y
K
F
M
N
x
l
y
K
F
M
N
o
x
l
抛物线的标准方程
一般地,我们把顶点在原点、焦点F 在坐标轴上的抛物线的方程叫做抛物线的标准方程.
y
K
F
M
N
o
x
l
方程 y2 = 2px(p>0)叫做抛物线的标准方程.
其中p为正常数,它的几何意义是:焦点到准线的距离.
若改用下面不同的建系方法, 请类比猜测标准方程分别是什么?
y
x
o
y
x
o
y
x
o
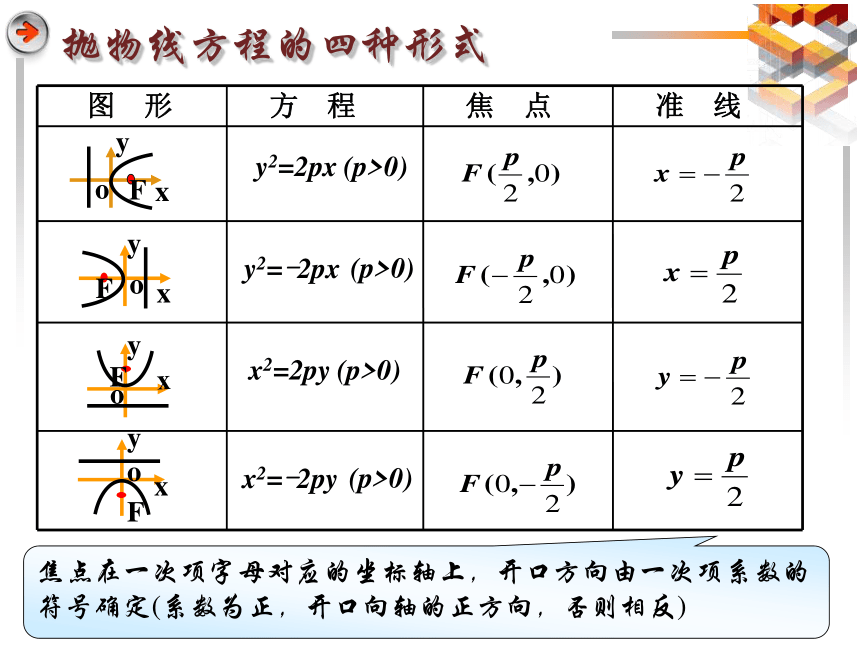
抛物线方程的四种形式
F
x
o
F
x
o
y
F
x
o
y
F
x
o
y
图 形
方 程
焦 点
准 线
y2=2px
(p>0)
y
y2=-2px
(p>0)
x2=2py
(p>0)
x2=-2py
(p>0)
焦点在一次项字母对应的坐标轴上,开口方向由一次项系数的符号确定(系数为正,开口向轴的正方向,否则相反)
抛物线的简单几何性质
研究角度:范围、对称性、顶点、离心率
研究对象:y2=2px(p>0)
(1) 范围:x≥0,y∈R
因为p>0,由方程可知x≥0,所以抛物线在y轴的右侧,当x的值增大时,|y|也增大,这说明抛物线向右上方和右下方无限延伸.
(2)对称性:关于x轴对称
以-y代y,方程不变,所以抛物线关于x轴对称.我们把抛物线的对称轴叫做抛物线的轴.
(3)顶点:原点
在方程中,当y=0时x=0,因此抛物线的顶点就是坐标原点. 抛物线与它的轴的交点叫做抛物线的顶点.
(4)离心率:e=1
抛物线上的点与焦点的距离和它到准线的距离的比,叫做抛物线的离心率,用e表示,由抛物线的定义可知,e=1
如何定义抛物线的离心率?
基本应用1.由标准方程求特征量
不要误认为y=ax2是标准方程.
基本应用1.求抛物线的标准方程
先看开口、再定p值
p始终是正数!
y2=12x
y2=x
y2=4x 或 y2= -4x
或 x2=4y 或 x2= -4y
求抛物线的标准方程
基本应用2 利用抛物线定义求轨迹
9.求到点A(-1,0)和直线x=3距离相等的点的轨迹方程。
抛物线不在标准位置时,不能套用标准方程公式! 只能用抛物线定义解。
10. P到点(1,1)与到直线2x+3y-5=0的距离相等,则点P的轨迹是 .其方程为:
8. 点M与点F(4,0)的距离比它到直线l:x+5=0的距离小1,求点M的轨迹方程.
基本应用3. 利用定义解最值问题
点P(x0,y0)在抛物线内部 y02<2px0
点P(x0,y0)在抛物线外部 y02>2px0
F
x
o
Q
Q在抛物线外部
F
x
o
Q
Q在抛物线内部
M
M’
M是线段FQ与抛物线的交点
M
M’
M是直线y=y0与抛物线的交点
不必死记,理解原理即可
方程
图
形
范围
对称性
顶点
焦半径
焦点弦的长度
y2 = 2px
(p>0)
y2 = -2px
(p>0)
x2 = 2py
(p>0)
x2 = -2py
(p>0)
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
x≥0
y∈R
x≤0
y∈R
x∈R
y≥0
y≤0
x∈R
l
F
y
x
O
关于x轴对称
关于x轴对称
关于y轴对称
关于y轴对称
(0,0)
(0,0)
(0,0)
(0,0)
小结
1.若抛物线的焦点为(2,2),准线方程为x+y-1=0,求此抛物线方程.
2.已知圆A:(x+2)2+y2=1与定直线l:x=1且动圆P和圆A外切并与直线l 相切,求动圆的圆心P的轨迹方程.
2010-12-6作业
抛物线
定义与标准方程
温故知新
抛物线定义:平面内与一个定点F和一条定直线l(l不经过点F)距离相等点的轨迹叫做抛物线
F1
F2
M
y
x
l
y
x
F1
F2
M
l
F
l
M
抛物线的方程
y
o
F
M
N
x
设一个定点F到一条定直线l的距离为常数p (p>0),
如何建立直角坐标系,求出抛物线的方程呢?
y
K
F
M
N
x
l
y
K
F
M
N
o
x
l
抛物线的标准方程
一般地,我们把顶点在原点、焦点F 在坐标轴上的抛物线的方程叫做抛物线的标准方程.
y
K
F
M
N
o
x
l
方程 y2 = 2px(p>0)叫做抛物线的标准方程.
其中p为正常数,它的几何意义是:焦点到准线的距离.
若改用下面不同的建系方法, 请类比猜测标准方程分别是什么?
y
x
o
y
x
o
y
x
o
抛物线方程的四种形式
F
x
o
F
x
o
y
F
x
o
y
F
x
o
y
图 形
方 程
焦 点
准 线
y2=2px
(p>0)
y
y2=-2px
(p>0)
x2=2py
(p>0)
x2=-2py
(p>0)
焦点在一次项字母对应的坐标轴上,开口方向由一次项系数的符号确定(系数为正,开口向轴的正方向,否则相反)
抛物线的简单几何性质
研究角度:范围、对称性、顶点、离心率
研究对象:y2=2px(p>0)
(1) 范围:x≥0,y∈R
因为p>0,由方程可知x≥0,所以抛物线在y轴的右侧,当x的值增大时,|y|也增大,这说明抛物线向右上方和右下方无限延伸.
(2)对称性:关于x轴对称
以-y代y,方程不变,所以抛物线关于x轴对称.我们把抛物线的对称轴叫做抛物线的轴.
(3)顶点:原点
在方程中,当y=0时x=0,因此抛物线的顶点就是坐标原点. 抛物线与它的轴的交点叫做抛物线的顶点.
(4)离心率:e=1
抛物线上的点与焦点的距离和它到准线的距离的比,叫做抛物线的离心率,用e表示,由抛物线的定义可知,e=1
如何定义抛物线的离心率?
基本应用1.由标准方程求特征量
不要误认为y=ax2是标准方程.
基本应用1.求抛物线的标准方程
先看开口、再定p值
p始终是正数!
y2=12x
y2=x
y2=4x 或 y2= -4x
或 x2=4y 或 x2= -4y
求抛物线的标准方程
基本应用2 利用抛物线定义求轨迹
9.求到点A(-1,0)和直线x=3距离相等的点的轨迹方程。
抛物线不在标准位置时,不能套用标准方程公式! 只能用抛物线定义解。
10. P到点(1,1)与到直线2x+3y-5=0的距离相等,则点P的轨迹是 .其方程为:
8. 点M与点F(4,0)的距离比它到直线l:x+5=0的距离小1,求点M的轨迹方程.
基本应用3. 利用定义解最值问题
点P(x0,y0)在抛物线内部 y02<2px0
点P(x0,y0)在抛物线外部 y02>2px0
F
x
o
Q
Q在抛物线外部
F
x
o
Q
Q在抛物线内部
M
M’
M是线段FQ与抛物线的交点
M
M’
M是直线y=y0与抛物线的交点
不必死记,理解原理即可
方程
图
形
范围
对称性
顶点
焦半径
焦点弦的长度
y2 = 2px
(p>0)
y2 = -2px
(p>0)
x2 = 2py
(p>0)
x2 = -2py
(p>0)
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
x≥0
y∈R
x≤0
y∈R
x∈R
y≥0
y≤0
x∈R
l
F
y
x
O
关于x轴对称
关于x轴对称
关于y轴对称
关于y轴对称
(0,0)
(0,0)
(0,0)
(0,0)
小结
1.若抛物线的焦点为(2,2),准线方程为x+y-1=0,求此抛物线方程.
2.已知圆A:(x+2)2+y2=1与定直线l:x=1且动圆P和圆A外切并与直线l 相切,求动圆的圆心P的轨迹方程.
2010-12-6作业
