北师大版高一对数

(共22张PPT)
§5.1 对数函数的概念
复习提问
1、对数的概念
一般地，如果
，那么数 b叫做
以a为底 N的对数，记作
a叫做对数的底数，N叫做真数
2、指数函数的定义
形如y = ax (a 0，且a 1)的函数叫做指数函数，
其中x是自变量 .函数的定义域是R .
3、指数型函数:
形如y = kax (k∈R,a>0且a≠1)的函数
马王堆女尸千年不腐之迷：1973年，马王堆考古发现震惊世界，专家发觉西汉辛追遗体时，形体完整，全身润泽，皮肤仍然有弹性，关节还可以活动，骨质比现在60岁的正常人还好，是世界上发现的首例历史悠久的湿尸。大家知道，世界发现的不腐之尸，一般在干燥的环境风干而成，而辛追夫人却是在湿润的环境中保存了2000多年，人们最关注的是怎么鉴定尸体的年份？考古学家怎么计算出古长沙国丞相夫人辛追“沉睡”了2200年？
考古学家一般通过提取附着在出土文物、古遗址
上死亡的残留物，利用 估计
出土文物或古遗址的年代.
t 能不能看成是 P 的函数？
根据问题的实际意义可知，对于每一个碳14含量P，
通过对应关系 都有唯一
确定的年代 t 与它对应，所以，t 是P的函数.
创设情景、提出问题
拉面模型： 厨师在做拉面时，由1根拉成2根，2
根 拉成4根，··· 1根这样的面拉x次会得到
多少根面条？
根据对数的定义，这个函数写成对数式的
形式是什么？
拉面的次数x是否也是面条的根数y的函数呢？
问题2：
问题1：
是
用y表示函数,x表示自变量， 这个函数的
解析式是什么？
问题3：
§5.1 对数函数
一 、对数函数的定义：
前面两个例子中用a代替 或2，则
得到一般性的结论：
形如
我们知道真数必须要大于0
所以函数的定义域是（0，+∞）。
叫做对数函数
2、由于对数函数的自变量是对数的真数
注：1、对数函数对底数的限制：
(a 0，且a 1)
(a 0，且a 1)
练习一：判断以下函数是对数函数的是 （ ）
（1） y=log2(3x-2) （2） y=log(x-1)x
（3） y=log0.3x2 （4） y=lnx
（5） y=3log2x + 5
4
注意：1、 对数函数的真数为自变量x
2、 对数函数对底数的限制(a>0,a≠1)
3 、系数必须为1，项数只有1项
以10为底的对数函数叫常用对数函数记作y=lgx
以无理数e为底对数函数叫自然对数函数记作y=lnx
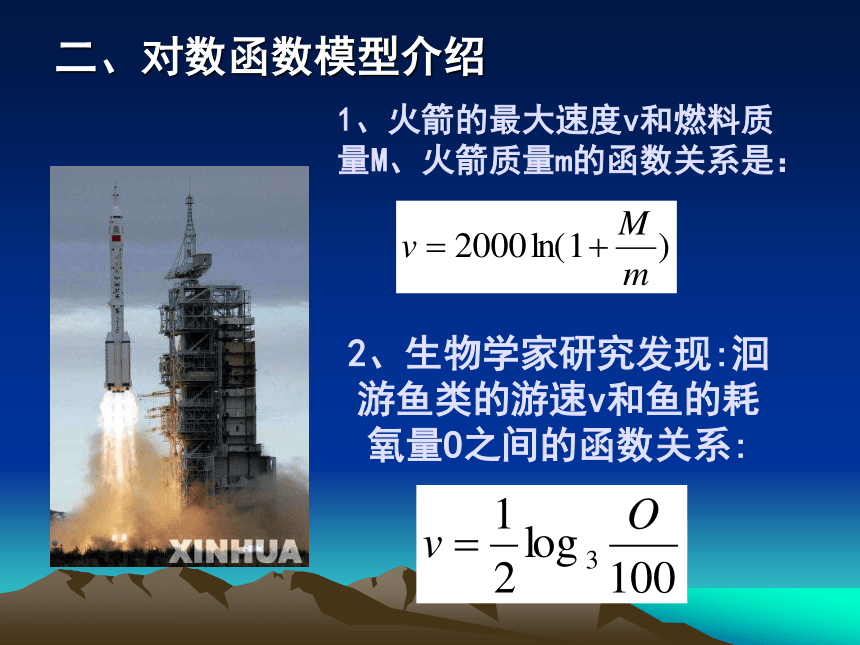
二、对数函数模型介绍
1、火箭的最大速度v和燃料质量M、火箭质量m的函数关系是：
2、生物学家研究发现:洄游鱼类的游速v和鱼的耗氧量O之间的函数关系:
三、新知探究:
指数函数y=ax和对数函数y=logax有什么关系
指数函数y=ax 和对数函数 x=logay刻画的是同一对变量 x, y之间的关系
分析:
在指数函数y=ax 中,x 是自变量, y是x的函数, 其定义域是R,值域是 (0,+
在对数函数 x=logay中, y是自变量, x是y 的函数,其定义域是 (0,+ ,值域是R
不同点:
归纳新定义——反函数
归纳反函数的定义
像y=ax和x=logay 这样的两个函数叫作互为反函数
通常情况下,用x 表示自变量, y表示函数,
所以,指数函数y=ax 是对数函数 y=logax的反函数;
同时,对数函数y=logax 是指数函数y=ax的反函数
例如：函数y=3x
的反函数是y=log3x
四、研究学习 画对数函数y=log2x的图像
方法：列表、描点、连线
列表对比，发现关系
x
Y=2x
…
…
-3
0
1
2
3
…
…
1/8
1/4
1
2
8
-2
1/2
-1
4
x
Y=log2x
…
…
1/8
1/4
1/2
1
2
4
8
…
…
-3
-2
-1
0
1
2
3
x
y
O
1
1
2
2
3
3
4
4
5
5
6
7
y=log2x
y=x
- 1
-1
-2
●
●
●
●
●
●
●
●
y=2x
动画演示
结论探讨:
2、互为反函数的两个函数其中一个函数图象
过点（a,b），则另一个必过点（b,a）
1、互为反函数的两个函数图象关于y=x对称
3、 的图像在（0，+∞）单调递增
例1:求下列函数的定义域:
(1) y=logax2 (2) y=loga(4-x)
解:
(1)因为x2>0,所以x≠ ,即函数y=logax2的定义域为
- (0,+
(2)因为 4-x>0,所以x<4,即函数y=loga(4-x)的定义域为
(- 4)
(3) y=log(x-1)(3-x)
五、例题分析
(3) 3-x>0
因为 x-1>0
x-1≠
所以 1函数y=log(x-1)(3-x)的定义域为:
(1,2)
例2:
写出下列函数的反函数:
(1) y=lgx (2) y=log2x （x>4）
(3) y=5x (4) y=(0.8)x
（5） ( -1解:
对数函数y=lgx ，它的底数是10，
所以它的反函数是指数函数y=10x
y=2x
(3)
y=log5x
y=log0.8x
(4)
(2)因为y=log2x 在（0，+∞）上是单调递增x>4,y>2,所以反函数是 （x>2）
注意：反函数的定义域是原函数的值域，
反函数的值域是原函数的定义域
（5）由题意：
互换x,y的位置
因为 -1所以 1< y < 3
所以反函数为 （1例3 已知y=f(x)是函数g(x)= 的反函数，且f(x)的图像过点（-1,0.5），试求g(x)的解析式 .
法二因为f(x)是g(x)的反函数
法一：依题意f(x)是g(x)反函数
思考：若将g(x)的解析式改为
,则求g(x)的解析式呢
f(x)的图像
课堂小结
1、对数函数的概念
2、对数函数的反函数
3、函数y=log2x图像画法
作业
课堂作业: 习题3-5 A组1、3
课外作业:
1.看书P89—P93，梳理对数函数的定义、反函数概念等知识点.
2.思考：
(1)对比指数函数的定义、图象和性质，预习课本p90-93,了解和对数函数的图象和性质.
(2)思考题：
若函数
求a的取值范围.