人教版八年级下册18.1.1.1平行四边形的性质课件(38张ppt)
文档属性
| 名称 | 人教版八年级下册18.1.1.1平行四边形的性质课件(38张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 902.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-04 09:52:28 | ||
图片预览







文档简介
(共38张PPT)
18.1.1.1
平行四边形的性质
学习目标
1
2
3
理解平行四边形的定义,平行四边形的边、角的性质
理解并掌握平行线间的距离
体会几何研究的一般思路与方法,感受转化思想
学习重难点
重点
难点
掌握平行四边形的定义和对边相等、对角相等的两条性质
根据平行四边形的性质进行简单的计算和证明
借助情境,回顾概念
A
B
C
D
平行四边形用“
”表示,如图,
平行四边形ABCD记作“
ABCD”.
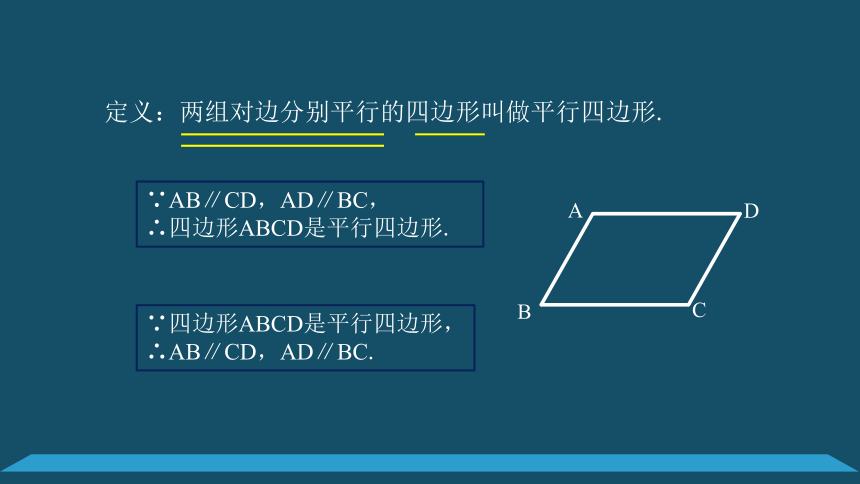
定义:两组对边分别平行的四边形叫做平行四边形.
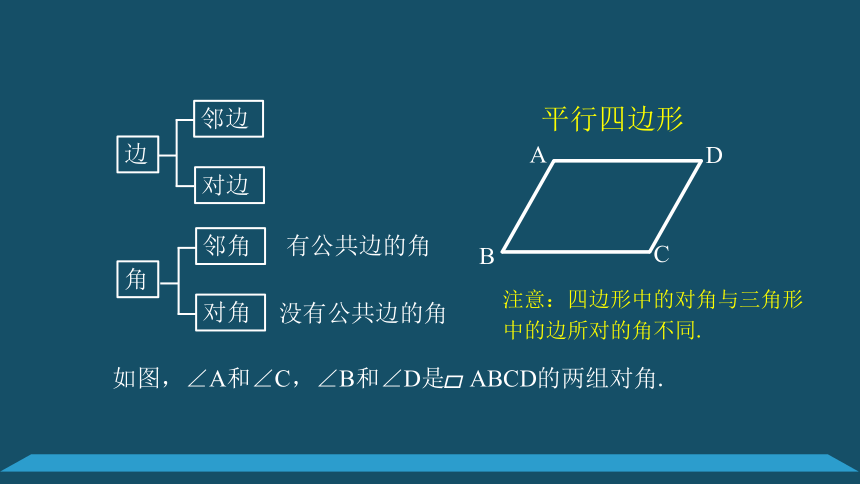
边
对边
邻边
有公共顶点的边
没有公共顶点的边
如图,AB和CD,AD和BC是
ABCD的两组对边.
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC.
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
定义:两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
A
B
C
D
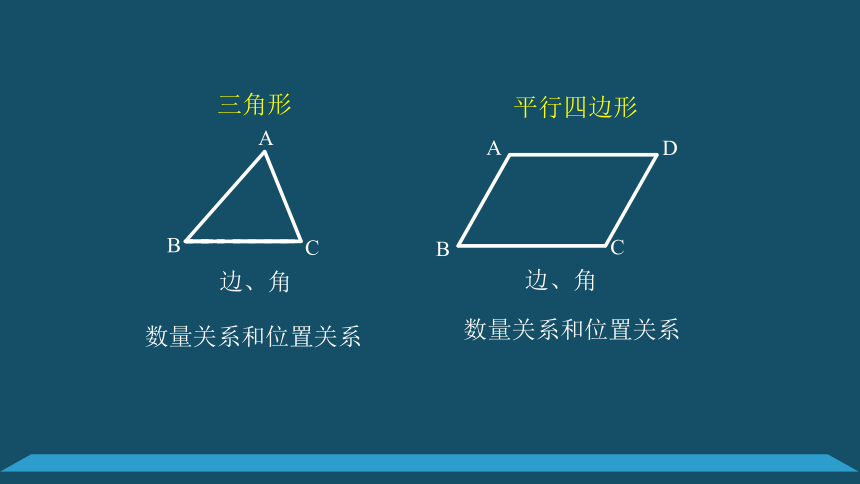
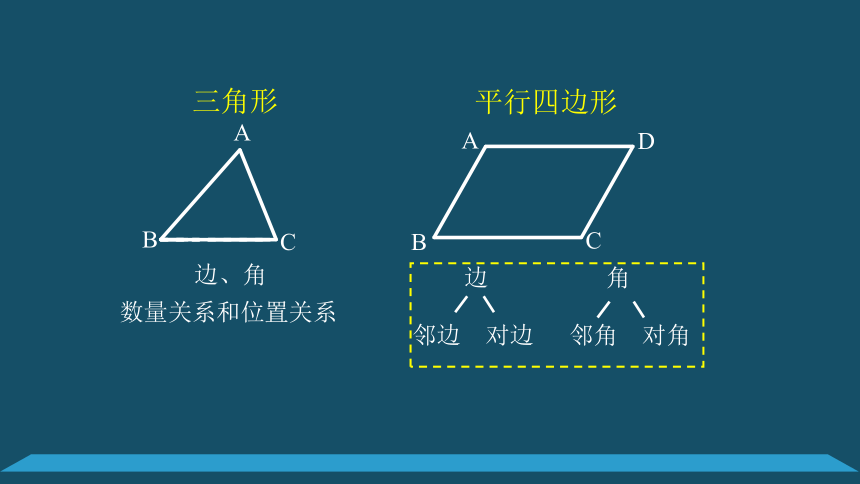
边、角
数量关系和位置关系
平行四边形
数量关系和位置关系
边、角
三角形
B
A
C
注意:四边形中的对角与三角形中的边所对的角不同.
平行四边形
边
对边
邻边
角
对角
邻角
有公共边的角
没有公共边的角
A
B
C
D
如图,∠A和∠C,∠B和∠D是
ABCD的两组对角.
边
邻角
边、角
邻边
对边
数量关系和位置关系
角
平行四边形
对角
A
B
C
D
三角形
B
A
C
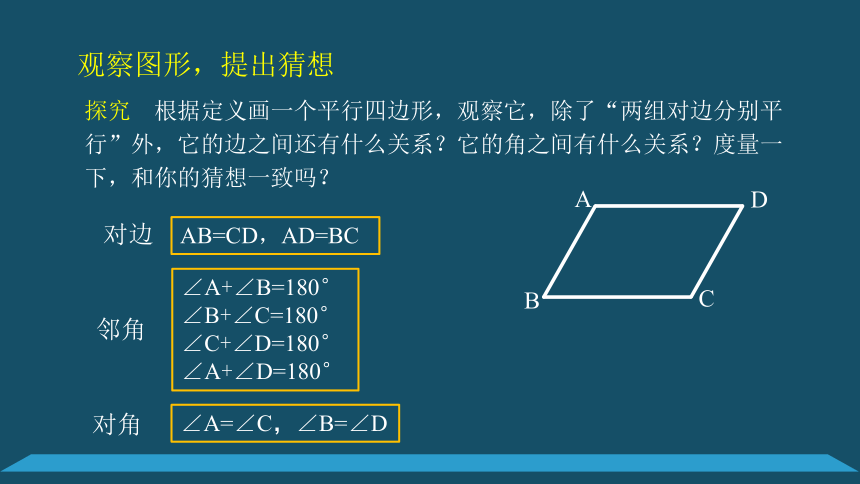
探究
根据定义画一个平行四边形,观察它,除了“两组对边分别平行”外,它的边之间还有什么关系?它的角之间有什么关系?度量一下,和你的猜想一致吗?
观察图形,提出猜想
对边
AB=CD,AD=BC
邻角
∠A+∠B=180°
∠B+∠C=180°
∠C+∠D=180°
∠A+∠D=180°
∠A=∠C,∠B=∠D
对角
A
B
C
D
平行四边形的对边相等;
平行四边形的邻角互补;
平行四边形的对角相等.
猜想:
A
B
C
D
猜想:平行四边形的对边相等.
如果一个四边形是平行四边形,那么这个四边形的对边相等.
证明猜想,得出结论
题设
结论
已知:如图,四边形ABCD是平行四边形.
求证:AB=CD,AD=BC.
A
B
C
D
3
4
分析:
AD∥BC,AB∥CD
2
1
∠1=∠2,∠3=∠4
AC为公共边
四边形ABCD是平行四边形
定义
△ABC≌△CDA(ASA)
AB=CD,BC=AD
A
B
C
D
线段相等
连接AC,构造全等三角形
证明:如图,连接AC.
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD.
∴∠1=∠2,∠3=∠4.
又AC=CA,
∴△ABC≌△CDA.
∴AB=CD,AD=BC.
3
4
2
1
A
B
C
D
已知:如图,四边形ABCD是平行四边形.
求证:AB=CD,AD=BC.
性质:平行四边形的对边相等.
∵
四边形ABCD是平行四边形,
∴
AB=CD,AD=BC.
A
B
C
D
猜想:平行四边形的对角相等.
如果一个四边形是平行四边形,那么这个四边形的对角相等.
题设
结论
已知:如图,四边形ABCD是平行四边形.
求证:∠A=∠C,∠B=∠D.
分析:
连接AC,构造全等三角形
角相等
A
B
C
D
∠1=∠2,∠3=∠4
分析:
△ABC≌△CDA(ASA)
AD∥BC,AB∥CD
,AC为公共边
四边形ABCD是平行四边形
∠B=∠D
定义
∠BAD=∠DCB
∠2+∠3=∠1+∠4
3
4
2
1
A
B
C
D
证明:如图,连接AC.
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD.
∴∠1=∠2,∠3=∠4.
∴∠2+∠3=∠1+∠4.
即∠BAD=∠DCB.
∵AC=CA,
∴△ABC≌△CDA.
∴∠B=∠D.
3
4
2
1
A
B
C
D
已知:如图,四边形ABCD是平行四边形.
求证:∠A=∠C,∠B=∠D.
连接AC
连接BD
A
B
C
D
A
B
C
D
三角形全等
线段相等、角相等
添加辅助线
构造两个三角形
不添加辅助线,你能否证明其对角相等?
已知:如图,四边形ABCD是平行四边形.求证:∠A=∠C,∠B=∠D.
A
B
C
D
分析:
四边形ABCD是平行四边形
AB∥CD,AD∥BC
∠B+∠C=180°,∠A+∠B=180°
∠A=∠C
定义
证明:∵
四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC.
∴∠B+∠C=180°,
∠A+∠B=180°.
∴∠A=∠C.
同理∠B=∠D.
A
B
C
D
已知:如图,四边形ABCD是平行四边形.求证:∠A=∠C,∠B=∠D.
性质:平行四边形的对角相等.
∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D.
A
B
C
D
平行四边形的性质
对边平行
边
角
对边相等
邻角互补
对角相等
对边平行且相等
位置关系、数量关系
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC.
又AB=5,BC=3,
∴
ABCD的周长=AB+BC+CD+DA
=2(AB+BC)
=16.
A
C
B
D
典例分析,巩固新知
练习1
在
ABCD中,已知AB=5,BC=3,求它的周长.
练习2
在
ABCD中,已知∠A=38°,求其余各内角的度数.
解:∵
四边形ABCD是平行四边形,
∴
∠A=∠C,∠B=∠D,AB∥CD.
∴
∠A+∠D=180°.
∵
∠A=38°,
∴
∠C=38°,∠D=142°.
∴
∠B=142°.
A
C
B
D
证法一:∵四边形ABCD是平行四边形,
∴AD=CB,∠A=∠C.
∵DE⊥AB,BF⊥CD,
∴∠AED=∠CFB=90°.
∴△ADE≌△CBF.
∴AE=CF.
例1
如图,在
ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.
求证:
AE=CF.
A
F
E
C
B
D
证法二:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠EDF+∠DEB=180°.
∵DE⊥AB,∴∠DEB=90°.∴∠EDF=90°.
∵BF⊥CD,∴∠BFC=90°.
∴∠EDF=∠BFC.
∴DE∥FB.
又AB∥CD,∴四边形EBFD是平行四边形.
∴EB=FD.∴AB-EB=CD-FD.
即AE=CF.
A
F
E
C
B
D
三角形全等
线段相等
平行四边形
线段相等
对应边相等
对边相等
如图,若a∥b,c∥d,c,d与a,b分别相交于A,B,C,D四点,则AB=CD.
A
B
D
C
a
b
c
d
四边形ABDC是平行四边形
AB=CD
a∥b,c∥d
平行四边形的定义
平行四边形的对边相等
两条平行线之间的任何两条平行线段都相等.
A
B
D
C
a
b
c
d
AB=CD
AB∥CD
四边形ABDC是平行四边形
如图,a∥b,A,C为a上任意两点,点A到直线b的距离和点C到直线b的距离相等吗?
平行四边形的定义
平行四边形的对边相等
,a∥b
A
C
B
D
a
b
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
如图,
a∥b,A是a上的任意一点,
AB⊥b
,B是垂足,线段AB的长就是a
,
b之间的距离.
A
B
a
b
课堂总结
平行四边形
定义
性质
两组对边分别平行的四边形叫做平行四边形.
平行四边形的对边平行;
平行四边形的对边相等;
平行四边形的邻角互补;
平行四边形的对角相等.
课堂总结
定义
性质
两条平行线间的距离
边
角
对边平行且相等
邻角互补、对角相等
数量关系
位置关系
平行四边形
课后作业
A
B
C
D
1.如图,剪两张对边平行的纸条,随意交叉叠放在一起,
重合部分构成了一个四边形.
转动其中一张纸条,线段AD和BC的长度有什么关系?为什么?
课后作业
2.如果一个四边形ABCD是平行四边形,AB=6,且AB的长是
ABCD的周长的
,那么BC的长是多少?
再
见
18.1.1.1
平行四边形的性质
学习目标
1
2
3
理解平行四边形的定义,平行四边形的边、角的性质
理解并掌握平行线间的距离
体会几何研究的一般思路与方法,感受转化思想
学习重难点
重点
难点
掌握平行四边形的定义和对边相等、对角相等的两条性质
根据平行四边形的性质进行简单的计算和证明
借助情境,回顾概念
A
B
C
D
平行四边形用“
”表示,如图,
平行四边形ABCD记作“
ABCD”.
定义:两组对边分别平行的四边形叫做平行四边形.
边
对边
邻边
有公共顶点的边
没有公共顶点的边
如图,AB和CD,AD和BC是
ABCD的两组对边.
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC.
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
定义:两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
A
B
C
D
边、角
数量关系和位置关系
平行四边形
数量关系和位置关系
边、角
三角形
B
A
C
注意:四边形中的对角与三角形中的边所对的角不同.
平行四边形
边
对边
邻边
角
对角
邻角
有公共边的角
没有公共边的角
A
B
C
D
如图,∠A和∠C,∠B和∠D是
ABCD的两组对角.
边
邻角
边、角
邻边
对边
数量关系和位置关系
角
平行四边形
对角
A
B
C
D
三角形
B
A
C
探究
根据定义画一个平行四边形,观察它,除了“两组对边分别平行”外,它的边之间还有什么关系?它的角之间有什么关系?度量一下,和你的猜想一致吗?
观察图形,提出猜想
对边
AB=CD,AD=BC
邻角
∠A+∠B=180°
∠B+∠C=180°
∠C+∠D=180°
∠A+∠D=180°
∠A=∠C,∠B=∠D
对角
A
B
C
D
平行四边形的对边相等;
平行四边形的邻角互补;
平行四边形的对角相等.
猜想:
A
B
C
D
猜想:平行四边形的对边相等.
如果一个四边形是平行四边形,那么这个四边形的对边相等.
证明猜想,得出结论
题设
结论
已知:如图,四边形ABCD是平行四边形.
求证:AB=CD,AD=BC.
A
B
C
D
3
4
分析:
AD∥BC,AB∥CD
2
1
∠1=∠2,∠3=∠4
AC为公共边
四边形ABCD是平行四边形
定义
△ABC≌△CDA(ASA)
AB=CD,BC=AD
A
B
C
D
线段相等
连接AC,构造全等三角形
证明:如图,连接AC.
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD.
∴∠1=∠2,∠3=∠4.
又AC=CA,
∴△ABC≌△CDA.
∴AB=CD,AD=BC.
3
4
2
1
A
B
C
D
已知:如图,四边形ABCD是平行四边形.
求证:AB=CD,AD=BC.
性质:平行四边形的对边相等.
∵
四边形ABCD是平行四边形,
∴
AB=CD,AD=BC.
A
B
C
D
猜想:平行四边形的对角相等.
如果一个四边形是平行四边形,那么这个四边形的对角相等.
题设
结论
已知:如图,四边形ABCD是平行四边形.
求证:∠A=∠C,∠B=∠D.
分析:
连接AC,构造全等三角形
角相等
A
B
C
D
∠1=∠2,∠3=∠4
分析:
△ABC≌△CDA(ASA)
AD∥BC,AB∥CD
,AC为公共边
四边形ABCD是平行四边形
∠B=∠D
定义
∠BAD=∠DCB
∠2+∠3=∠1+∠4
3
4
2
1
A
B
C
D
证明:如图,连接AC.
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD.
∴∠1=∠2,∠3=∠4.
∴∠2+∠3=∠1+∠4.
即∠BAD=∠DCB.
∵AC=CA,
∴△ABC≌△CDA.
∴∠B=∠D.
3
4
2
1
A
B
C
D
已知:如图,四边形ABCD是平行四边形.
求证:∠A=∠C,∠B=∠D.
连接AC
连接BD
A
B
C
D
A
B
C
D
三角形全等
线段相等、角相等
添加辅助线
构造两个三角形
不添加辅助线,你能否证明其对角相等?
已知:如图,四边形ABCD是平行四边形.求证:∠A=∠C,∠B=∠D.
A
B
C
D
分析:
四边形ABCD是平行四边形
AB∥CD,AD∥BC
∠B+∠C=180°,∠A+∠B=180°
∠A=∠C
定义
证明:∵
四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC.
∴∠B+∠C=180°,
∠A+∠B=180°.
∴∠A=∠C.
同理∠B=∠D.
A
B
C
D
已知:如图,四边形ABCD是平行四边形.求证:∠A=∠C,∠B=∠D.
性质:平行四边形的对角相等.
∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D.
A
B
C
D
平行四边形的性质
对边平行
边
角
对边相等
邻角互补
对角相等
对边平行且相等
位置关系、数量关系
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC.
又AB=5,BC=3,
∴
ABCD的周长=AB+BC+CD+DA
=2(AB+BC)
=16.
A
C
B
D
典例分析,巩固新知
练习1
在
ABCD中,已知AB=5,BC=3,求它的周长.
练习2
在
ABCD中,已知∠A=38°,求其余各内角的度数.
解:∵
四边形ABCD是平行四边形,
∴
∠A=∠C,∠B=∠D,AB∥CD.
∴
∠A+∠D=180°.
∵
∠A=38°,
∴
∠C=38°,∠D=142°.
∴
∠B=142°.
A
C
B
D
证法一:∵四边形ABCD是平行四边形,
∴AD=CB,∠A=∠C.
∵DE⊥AB,BF⊥CD,
∴∠AED=∠CFB=90°.
∴△ADE≌△CBF.
∴AE=CF.
例1
如图,在
ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.
求证:
AE=CF.
A
F
E
C
B
D
证法二:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠EDF+∠DEB=180°.
∵DE⊥AB,∴∠DEB=90°.∴∠EDF=90°.
∵BF⊥CD,∴∠BFC=90°.
∴∠EDF=∠BFC.
∴DE∥FB.
又AB∥CD,∴四边形EBFD是平行四边形.
∴EB=FD.∴AB-EB=CD-FD.
即AE=CF.
A
F
E
C
B
D
三角形全等
线段相等
平行四边形
线段相等
对应边相等
对边相等
如图,若a∥b,c∥d,c,d与a,b分别相交于A,B,C,D四点,则AB=CD.
A
B
D
C
a
b
c
d
四边形ABDC是平行四边形
AB=CD
a∥b,c∥d
平行四边形的定义
平行四边形的对边相等
两条平行线之间的任何两条平行线段都相等.
A
B
D
C
a
b
c
d
AB=CD
AB∥CD
四边形ABDC是平行四边形
如图,a∥b,A,C为a上任意两点,点A到直线b的距离和点C到直线b的距离相等吗?
平行四边形的定义
平行四边形的对边相等
,a∥b
A
C
B
D
a
b
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
如图,
a∥b,A是a上的任意一点,
AB⊥b
,B是垂足,线段AB的长就是a
,
b之间的距离.
A
B
a
b
课堂总结
平行四边形
定义
性质
两组对边分别平行的四边形叫做平行四边形.
平行四边形的对边平行;
平行四边形的对边相等;
平行四边形的邻角互补;
平行四边形的对角相等.
课堂总结
定义
性质
两条平行线间的距离
边
角
对边平行且相等
邻角互补、对角相等
数量关系
位置关系
平行四边形
课后作业
A
B
C
D
1.如图,剪两张对边平行的纸条,随意交叉叠放在一起,
重合部分构成了一个四边形.
转动其中一张纸条,线段AD和BC的长度有什么关系?为什么?
课后作业
2.如果一个四边形ABCD是平行四边形,AB=6,且AB的长是
ABCD的周长的
,那么BC的长是多少?
再
见
