2021年湘教版七年级下册第4章《相交线与平行线》单元练习卷(word版含解析)
文档属性
| 名称 | 2021年湘教版七年级下册第4章《相交线与平行线》单元练习卷(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 171.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-03 00:00:00 | ||
图片预览



文档简介
2021年湘教版七年级下册第4章《相交线与平行线》单元练习卷
一.选择题
1.下列现象中,( )是平移.
A.“天问”探测器绕火星运动
B.篮球在空中飞行
C.电梯的上下移动
D.将一张纸对折
2.以下图形中,∠1与∠2表示邻补角的是( )
A.B.C.D.
3.下列说法正确的是( )
A.同角或等角的补角相等 B.内错角相等
C.同位角相等 D.同旁内角互补
4.已知∠A+∠B=180°,则下列说法正确的是( )
A.∠A与∠B是邻角 B.∠A与∠B是邻补角
C.∠A与∠B互为余角 D.∠A与∠B互为补角
5.如图,在△ABC中,CD是高,CM是中线,点C到AB边的距离是( )
A.CD的长 B.CA的长 C.CM的长 D.CB的长
6.下列说法,正确的是( )
A.两点之间,直线最短 B.过一点有且只有一条直线与已知直线平行
C.两直线平行,同旁内角相等 D.对顶角相等
7.如图,D,E,F分别在△ABC的三边上,能判定DE∥AC的条件是( )
A.∠1+∠2=180° B.∠1=∠3 C.∠2=∠4 D.∠3=∠C
8.如图,AB∥CD,∠A=100°,∠BCD=50°,∠ACB的度数为( )
A.25° B.30° C.45° D.50°
9.已知在同一平面内,直线a,b,c互相平行,直线a与b之间的距离是3cm,直线b与c之间的距离是5cm,那么直线a与c的距离是( )
A.2cm B.8cm C.8或2cm D.不能确定
10.如图,已知长方形纸片ABCD,点E,F在AD边上,点G,H在BC边上,分别沿EG,FH折叠,使点D和点A都落在点M处,若α+β=119°,则∠EMF的度数为( )
A.57° B.58° C.59° D.60°
二.填空题
11.如图,直线a,b相交于点O,若∠1+∠2=220°,则∠3= .
12.如图,直线a∥b,∠1=130°,则∠2的度数是 .
13.如图,已知直线AB、CD相交于点O,OE平分∠BOC,如果∠BOE=55°,那么∠AOD= 度.
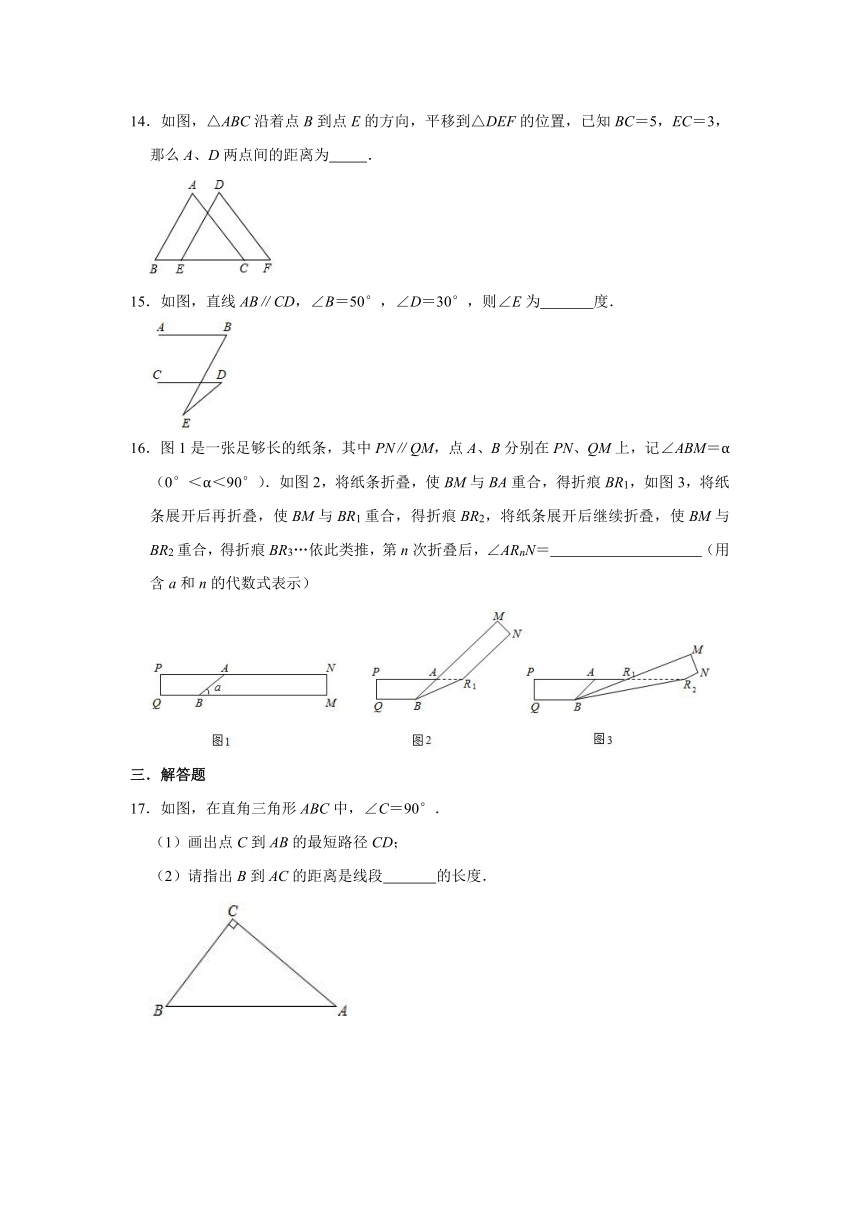
14.如图,△ABC沿着点B到点E的方向,平移到△DEF的位置,已知BC=5,EC=3,那么A、D两点间的距离为 .
15.如图,直线AB∥CD,∠B=50°,∠D=30°,则∠E为 度.
16.图1是一张足够长的纸条,其中PN∥QM,点A、B分别在PN、QM上,记∠ABM=α(0°<α<90°).如图2,将纸条折叠,使BM与BA重合,得折痕BR1,如图3,将纸条展开后再折叠,使BM与BR1重合,得折痕BR2,将纸条展开后继续折叠,使BM与BR2重合,得折痕BR3…依此类推,第n次折叠后,∠ARnN= (用含a和n的代数式表示)
三.解答题
17.如图,在直角三角形ABC中,∠C=90°.
(1)画出点C到AB的最短路径CD;
(2)请指出B到AC的距离是线段 的长度.
18.如图,AB⊥AD,CD⊥AD,∠1=∠2,
求证:DF∥EA.
19.如图,AB∥CD,∠B=26°,∠D=39°,求∠BED的度数.完成以下解答过程中的空缺部分:解:过点E作EF∥AB,
∴∠B=∠ ( ).
∵∠B=26°(已知),
∴∠1= °(等量代换).
∵AB∥CD(已知),
∵EF∥AB(作辅助线),
∴EF∥CD.
∴∠D=∠ .
∵∠D=39°(已知),
∴∠2= °.
∴∠BED= °(等式性质).
20.如图,每个小正方形的边长都相等,△ABC的三个顶点都在格点(小正方形的顶点)上.
(1)平移△ABC,使顶点A平移到点D的位置,得到△DEF,画出△DEF;(点B的对应点为点E)
(2)已知每个小正方形的面积为单位1,求AC扫过的面积.
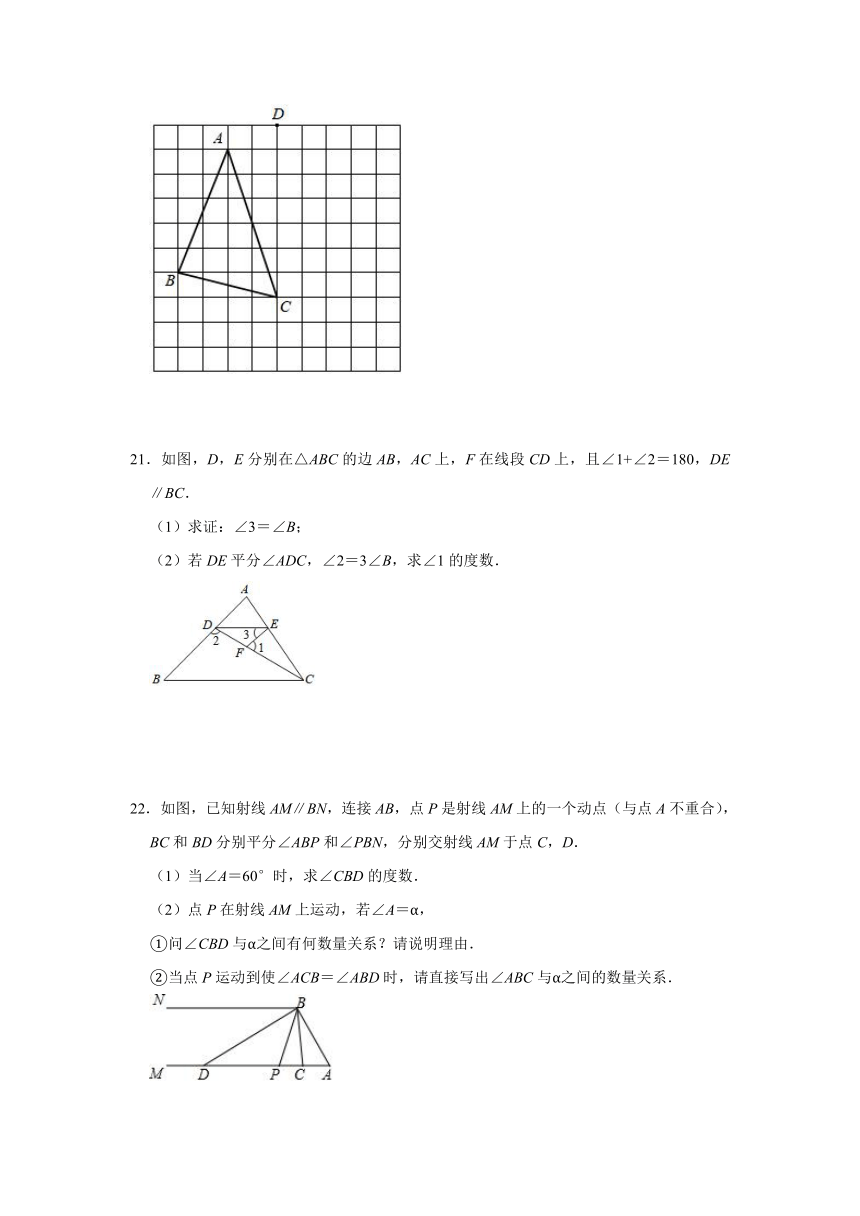
21.如图,D,E分别在△ABC的边AB,AC上,F在线段CD上,且∠1+∠2=180,DE∥BC.
(1)求证:∠3=∠B;
(2)若DE平分∠ADC,∠2=3∠B,求∠1的度数.
22.如图,已知射线AM∥BN,连接AB,点P是射线AM上的一个动点(与点A不重合),BC和BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)当∠A=60°时,求∠CBD的度数.
(2)点P在射线AM上运动,若∠A=α,
①问∠CBD与α之间有何数量关系?请说明理由.
②当点P运动到使∠ACB=∠ABD时,请直接写出∠ABC与α之间的数量关系.
参考答案
一.选择题
1.解:A.“天问”探测器绕火星运动不是平移;
B.篮球在空中飞行不是平移;
C.电梯的上下移动是平移;
D.将一张纸对折不是平移;
故选:C.
2.解:A.两个角是对顶角,故不是邻补角;
B、两个角是邻补角,符合题意;
C、两个角不存在公共边,故不是邻补角;
D、两个角不等于180°,故不是邻补角.
故选:B.
3.解:A,同角或等角的补角在任何情况下都相等,故A选项正确;
B,只有在两直线平行的情况下,内错角才相等,故B选项不正确;
C,只有在两直线平行的情况下,同位角才相等,故C选项不正确;
D,只有在两直线平行的情况下,同旁内角才互补,故D选项不正确.
故选:A.
4.解:A、∠A与∠B是邻角,两角度数之和不确定,故不符合题意;
B、∠A与∠B是邻补角,确定了∠A与∠B的位置关系,只是一种互补的特殊情形,故不符合题意;
C、∠A与∠B互为余角,即∠A+∠B=90°,故不符合题意;
D、∠A与∠B互为补角,即∠A+∠B=180°,符合题意;
故选:D.
5.解:∵直线外一点到这条直线的垂线段的长度叫这点到这条直线的距离,CD⊥AB,
∴点C到AB边的距离是线段CD的长.
故选:A.
6.解:A、两点之间,直线最短,错误,不符合题意;
B、过直线外一点有且只有一条直线与已知直线平行,错误,不符合题意;
C、两直线平行,同旁内角互补,错误,不符合题意;
D、对顶角相等,正确,符合题意.
故选:D.
7.解:A、当∠1+∠2=180°时,EF∥BC,不符合题意;
B、当∠1=∠3时,EF∥BC,不符合题意;
C、当∠2=∠4时,无法得到DE∥AC,不符合题意;
D、当∠3=∠C时,DE∥AC,符合题意.
故选:D.
8.解:∵AB∥CD,∠A=100°.
∴∠A+∠ACD=180°.
∴∠ACD=80°.
∵∠BCD=50°.
∴∠ACB=∠ACD﹣BCD=30°.
故选:B.
9.解:有两种情况,如图:
(1)直线a与c的距离是3厘米+5厘米=8厘米;
(2)直线a与c的距离是5厘米﹣3厘米=2厘米;
故选:C.
10.解:∵长方形ABCD,
∴AD∥BC,
∴∠DEG=α,∠AFH=β,
∴∠DEG+∠AFH=α+β=119°,
由折叠得:∠DEM=2∠DEG,∠AFM=2∠AFH,
∴∠DEG+∠AFM=2×119°=238°,
∴∠FEM+∠EFM=360°﹣238°=122°,
在△EFM中,
∠EMF=180°﹣(∠FEM+∠EFM)=180°﹣122°=58°,
故选:B.
二.填空题
11.解:∵∠1=∠2,∠1+∠2=220°,
∴∠1=∠2=110°,
∴∠3=180°﹣110°=70°,
故答案为:70°.
12.解:∵a∥b,
∴∠1+∠2=180°
∴∠1=130°,
∴∠2=180°﹣∠1=180°﹣130°=50°.
故答案为:50°.
13.解:∵OE平分∠BOC,∠BOE=50°,
∴∠BOC=2∠BOE=2×50°=100°,
∴∠AOC=∠BOC=100°.
故答案为:100.
14.解:∵BC=5,EC=3,
∴BE=BC﹣BE=2,
由平移的性质可知,AD=BE=2,
故答案为:2.
15.解:
∵AB∥CD,
∴∠B=∠1,
∵∠B=50°,
∴∠1=50°,
∵∠1=∠D+∠E,∠D=30°,
∴∠E=50°﹣30°=20°.
故答案为:20.
16.解:由折叠的性质可得:
∠AR1B=α,
∠AR2B==,
∠AR3B==,
...
∠ARn﹣1b=,
∴∠ARnN=180.
故答案为:180.
三.解答题
17.解:(1)根据题意,如图示,
(2)B到AC的距离是线段BC的长度,
故答案为:BC.
18.证明:∵AB⊥AD,CD⊥AD,
∴∠CDA=∠BAD=90°.
∴∠1+∠ADF=∠2+∠DAE.
∵∠1=∠2,
∴∠ADF=∠DAE.
∴DF∥EA.
19.解:过点E作EF∥AB,
∴∠B=∠1(两直线平行,内错角相等).
∵∠B=26°(已知),
∴∠1=26°(等量代换).
∴AB∥CD(已知),
∵EF∥AB(作辅助线),
∴EF∥CD.
∴∠D=∠2(两直线平行,内错角相等).
∵∠D=39°(已知),
∴∠2=39°(等量代换).
∴∠BED=65°(等式性质).
故答案为:1;两直线平行,内错角相等;26;2;39;65.
20.解:(1)如图所示,△DEF即为所求:
(2)AC扫过的面积==14.
21.解:(1)∵∠1+∠DFE=180°,∠1+∠2=180,
∴∠2=∠DFE,
∴AB∥EF,
∴∠3=∠ADE,
∵DE∥BC,
∴∠ADE=∠B,
∴∠3=∠B.
(2)∵DE平分∠ADC,
∴∠ADE=∠EDC,
∵DE∥BC,
∴∠ADE=∠EDC=∠B,
∵∠2=3∠B,∠2+∠ADE+∠EDC=180°,
∴5∠B=180°,
∴∠B=36°,
又∵∠3=∠B,
∴∠1=∠3+∠EDC=36°+36°=72°.
22.解:(1)∵AM∥BN,
∴∠A+∠ABN=180°,
又∵∠A=60°,
∴∠ABN=180°﹣∠A=120°.
∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBP=∠ABP,∠DBP=∠PBN,
∴∠CBD=∠CBP+∠DBP=∠ABP+∠PBN=∠ABN=60°.
(2)①∠CBD=,理由如下:
∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBP=∠ABP,∠DBP=∠PBN,
∴∠CBD=∠CBP+∠DBP=∠ABP+∠PBN=∠ABN,
∵AM∥BN,
∴∠A+∠ABN=180°,
∴∠ABN=180°﹣∠A,
∴∠CBD==.
②∵AM∥BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN,
∵BC,BD分别平分∠ABP和∠PBN,
∴∠ABC=∠ABN,
∵AM∥BN,
∴∠A+∠ABN=180°,
即∠ABN=180°﹣∠A=180°﹣α,
∴∠ABC=(180°﹣α)=45°﹣α.
一.选择题
1.下列现象中,( )是平移.
A.“天问”探测器绕火星运动
B.篮球在空中飞行
C.电梯的上下移动
D.将一张纸对折
2.以下图形中,∠1与∠2表示邻补角的是( )
A.B.C.D.
3.下列说法正确的是( )
A.同角或等角的补角相等 B.内错角相等
C.同位角相等 D.同旁内角互补
4.已知∠A+∠B=180°,则下列说法正确的是( )
A.∠A与∠B是邻角 B.∠A与∠B是邻补角
C.∠A与∠B互为余角 D.∠A与∠B互为补角
5.如图,在△ABC中,CD是高,CM是中线,点C到AB边的距离是( )
A.CD的长 B.CA的长 C.CM的长 D.CB的长
6.下列说法,正确的是( )
A.两点之间,直线最短 B.过一点有且只有一条直线与已知直线平行
C.两直线平行,同旁内角相等 D.对顶角相等
7.如图,D,E,F分别在△ABC的三边上,能判定DE∥AC的条件是( )
A.∠1+∠2=180° B.∠1=∠3 C.∠2=∠4 D.∠3=∠C
8.如图,AB∥CD,∠A=100°,∠BCD=50°,∠ACB的度数为( )
A.25° B.30° C.45° D.50°
9.已知在同一平面内,直线a,b,c互相平行,直线a与b之间的距离是3cm,直线b与c之间的距离是5cm,那么直线a与c的距离是( )
A.2cm B.8cm C.8或2cm D.不能确定
10.如图,已知长方形纸片ABCD,点E,F在AD边上,点G,H在BC边上,分别沿EG,FH折叠,使点D和点A都落在点M处,若α+β=119°,则∠EMF的度数为( )
A.57° B.58° C.59° D.60°
二.填空题
11.如图,直线a,b相交于点O,若∠1+∠2=220°,则∠3= .
12.如图,直线a∥b,∠1=130°,则∠2的度数是 .
13.如图,已知直线AB、CD相交于点O,OE平分∠BOC,如果∠BOE=55°,那么∠AOD= 度.
14.如图,△ABC沿着点B到点E的方向,平移到△DEF的位置,已知BC=5,EC=3,那么A、D两点间的距离为 .
15.如图,直线AB∥CD,∠B=50°,∠D=30°,则∠E为 度.
16.图1是一张足够长的纸条,其中PN∥QM,点A、B分别在PN、QM上,记∠ABM=α(0°<α<90°).如图2,将纸条折叠,使BM与BA重合,得折痕BR1,如图3,将纸条展开后再折叠,使BM与BR1重合,得折痕BR2,将纸条展开后继续折叠,使BM与BR2重合,得折痕BR3…依此类推,第n次折叠后,∠ARnN= (用含a和n的代数式表示)
三.解答题
17.如图,在直角三角形ABC中,∠C=90°.
(1)画出点C到AB的最短路径CD;
(2)请指出B到AC的距离是线段 的长度.
18.如图,AB⊥AD,CD⊥AD,∠1=∠2,
求证:DF∥EA.
19.如图,AB∥CD,∠B=26°,∠D=39°,求∠BED的度数.完成以下解答过程中的空缺部分:解:过点E作EF∥AB,
∴∠B=∠ ( ).
∵∠B=26°(已知),
∴∠1= °(等量代换).
∵AB∥CD(已知),
∵EF∥AB(作辅助线),
∴EF∥CD.
∴∠D=∠ .
∵∠D=39°(已知),
∴∠2= °.
∴∠BED= °(等式性质).
20.如图,每个小正方形的边长都相等,△ABC的三个顶点都在格点(小正方形的顶点)上.
(1)平移△ABC,使顶点A平移到点D的位置,得到△DEF,画出△DEF;(点B的对应点为点E)
(2)已知每个小正方形的面积为单位1,求AC扫过的面积.
21.如图,D,E分别在△ABC的边AB,AC上,F在线段CD上,且∠1+∠2=180,DE∥BC.
(1)求证:∠3=∠B;
(2)若DE平分∠ADC,∠2=3∠B,求∠1的度数.
22.如图,已知射线AM∥BN,连接AB,点P是射线AM上的一个动点(与点A不重合),BC和BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)当∠A=60°时,求∠CBD的度数.
(2)点P在射线AM上运动,若∠A=α,
①问∠CBD与α之间有何数量关系?请说明理由.
②当点P运动到使∠ACB=∠ABD时,请直接写出∠ABC与α之间的数量关系.
参考答案
一.选择题
1.解:A.“天问”探测器绕火星运动不是平移;
B.篮球在空中飞行不是平移;
C.电梯的上下移动是平移;
D.将一张纸对折不是平移;
故选:C.
2.解:A.两个角是对顶角,故不是邻补角;
B、两个角是邻补角,符合题意;
C、两个角不存在公共边,故不是邻补角;
D、两个角不等于180°,故不是邻补角.
故选:B.
3.解:A,同角或等角的补角在任何情况下都相等,故A选项正确;
B,只有在两直线平行的情况下,内错角才相等,故B选项不正确;
C,只有在两直线平行的情况下,同位角才相等,故C选项不正确;
D,只有在两直线平行的情况下,同旁内角才互补,故D选项不正确.
故选:A.
4.解:A、∠A与∠B是邻角,两角度数之和不确定,故不符合题意;
B、∠A与∠B是邻补角,确定了∠A与∠B的位置关系,只是一种互补的特殊情形,故不符合题意;
C、∠A与∠B互为余角,即∠A+∠B=90°,故不符合题意;
D、∠A与∠B互为补角,即∠A+∠B=180°,符合题意;
故选:D.
5.解:∵直线外一点到这条直线的垂线段的长度叫这点到这条直线的距离,CD⊥AB,
∴点C到AB边的距离是线段CD的长.
故选:A.
6.解:A、两点之间,直线最短,错误,不符合题意;
B、过直线外一点有且只有一条直线与已知直线平行,错误,不符合题意;
C、两直线平行,同旁内角互补,错误,不符合题意;
D、对顶角相等,正确,符合题意.
故选:D.
7.解:A、当∠1+∠2=180°时,EF∥BC,不符合题意;
B、当∠1=∠3时,EF∥BC,不符合题意;
C、当∠2=∠4时,无法得到DE∥AC,不符合题意;
D、当∠3=∠C时,DE∥AC,符合题意.
故选:D.
8.解:∵AB∥CD,∠A=100°.
∴∠A+∠ACD=180°.
∴∠ACD=80°.
∵∠BCD=50°.
∴∠ACB=∠ACD﹣BCD=30°.
故选:B.
9.解:有两种情况,如图:
(1)直线a与c的距离是3厘米+5厘米=8厘米;
(2)直线a与c的距离是5厘米﹣3厘米=2厘米;
故选:C.
10.解:∵长方形ABCD,
∴AD∥BC,
∴∠DEG=α,∠AFH=β,
∴∠DEG+∠AFH=α+β=119°,
由折叠得:∠DEM=2∠DEG,∠AFM=2∠AFH,
∴∠DEG+∠AFM=2×119°=238°,
∴∠FEM+∠EFM=360°﹣238°=122°,
在△EFM中,
∠EMF=180°﹣(∠FEM+∠EFM)=180°﹣122°=58°,
故选:B.
二.填空题
11.解:∵∠1=∠2,∠1+∠2=220°,
∴∠1=∠2=110°,
∴∠3=180°﹣110°=70°,
故答案为:70°.
12.解:∵a∥b,
∴∠1+∠2=180°
∴∠1=130°,
∴∠2=180°﹣∠1=180°﹣130°=50°.
故答案为:50°.
13.解:∵OE平分∠BOC,∠BOE=50°,
∴∠BOC=2∠BOE=2×50°=100°,
∴∠AOC=∠BOC=100°.
故答案为:100.
14.解:∵BC=5,EC=3,
∴BE=BC﹣BE=2,
由平移的性质可知,AD=BE=2,
故答案为:2.
15.解:
∵AB∥CD,
∴∠B=∠1,
∵∠B=50°,
∴∠1=50°,
∵∠1=∠D+∠E,∠D=30°,
∴∠E=50°﹣30°=20°.
故答案为:20.
16.解:由折叠的性质可得:
∠AR1B=α,
∠AR2B==,
∠AR3B==,
...
∠ARn﹣1b=,
∴∠ARnN=180.
故答案为:180.
三.解答题
17.解:(1)根据题意,如图示,
(2)B到AC的距离是线段BC的长度,
故答案为:BC.
18.证明:∵AB⊥AD,CD⊥AD,
∴∠CDA=∠BAD=90°.
∴∠1+∠ADF=∠2+∠DAE.
∵∠1=∠2,
∴∠ADF=∠DAE.
∴DF∥EA.
19.解:过点E作EF∥AB,
∴∠B=∠1(两直线平行,内错角相等).
∵∠B=26°(已知),
∴∠1=26°(等量代换).
∴AB∥CD(已知),
∵EF∥AB(作辅助线),
∴EF∥CD.
∴∠D=∠2(两直线平行,内错角相等).
∵∠D=39°(已知),
∴∠2=39°(等量代换).
∴∠BED=65°(等式性质).
故答案为:1;两直线平行,内错角相等;26;2;39;65.
20.解:(1)如图所示,△DEF即为所求:
(2)AC扫过的面积==14.
21.解:(1)∵∠1+∠DFE=180°,∠1+∠2=180,
∴∠2=∠DFE,
∴AB∥EF,
∴∠3=∠ADE,
∵DE∥BC,
∴∠ADE=∠B,
∴∠3=∠B.
(2)∵DE平分∠ADC,
∴∠ADE=∠EDC,
∵DE∥BC,
∴∠ADE=∠EDC=∠B,
∵∠2=3∠B,∠2+∠ADE+∠EDC=180°,
∴5∠B=180°,
∴∠B=36°,
又∵∠3=∠B,
∴∠1=∠3+∠EDC=36°+36°=72°.
22.解:(1)∵AM∥BN,
∴∠A+∠ABN=180°,
又∵∠A=60°,
∴∠ABN=180°﹣∠A=120°.
∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBP=∠ABP,∠DBP=∠PBN,
∴∠CBD=∠CBP+∠DBP=∠ABP+∠PBN=∠ABN=60°.
(2)①∠CBD=,理由如下:
∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBP=∠ABP,∠DBP=∠PBN,
∴∠CBD=∠CBP+∠DBP=∠ABP+∠PBN=∠ABN,
∵AM∥BN,
∴∠A+∠ABN=180°,
∴∠ABN=180°﹣∠A,
∴∠CBD==.
②∵AM∥BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN,
∵BC,BD分别平分∠ABP和∠PBN,
∴∠ABC=∠ABN,
∵AM∥BN,
∴∠A+∠ABN=180°,
即∠ABN=180°﹣∠A=180°﹣α,
∴∠ABC=(180°﹣α)=45°﹣α.
