陕西省渭南市尚德高中2020-2021学年高二下学期4月第一次质量检测数学(理)试卷 Word含答案
文档属性
| 名称 | 陕西省渭南市尚德高中2020-2021学年高二下学期4月第一次质量检测数学(理)试卷 Word含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 327.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-04 08:58:50 | ||
图片预览


文档简介
尚德中学高二(2022届)下第一次教学质量检测
数学(理)试题
第Ⅰ卷(选择题 共60分)
选择题(本大题共12小题,每小题5分,共60分)
1.复数在复平面上对应的点位于 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2.用反证法证明命题:“若能被5整除,则中至少有一个能被5整除”,那么假设的内容是 ( )
A. 都能被5整除 B. 都不能被5整除
C. 有一个能被5整除 D. 有一个不能被5整除
3.用数学归纳法证明时,第一步应验证不等式 ( )
A. B. C. D.
4.已知函数在点处的切线方程是 ( )
A. B.
C. D.
5.下列值等于1的是 ( )
A. B. C. D.
6.已知函数 ( )
A.0 B.﹣2 C.2e﹣3 D.e﹣3
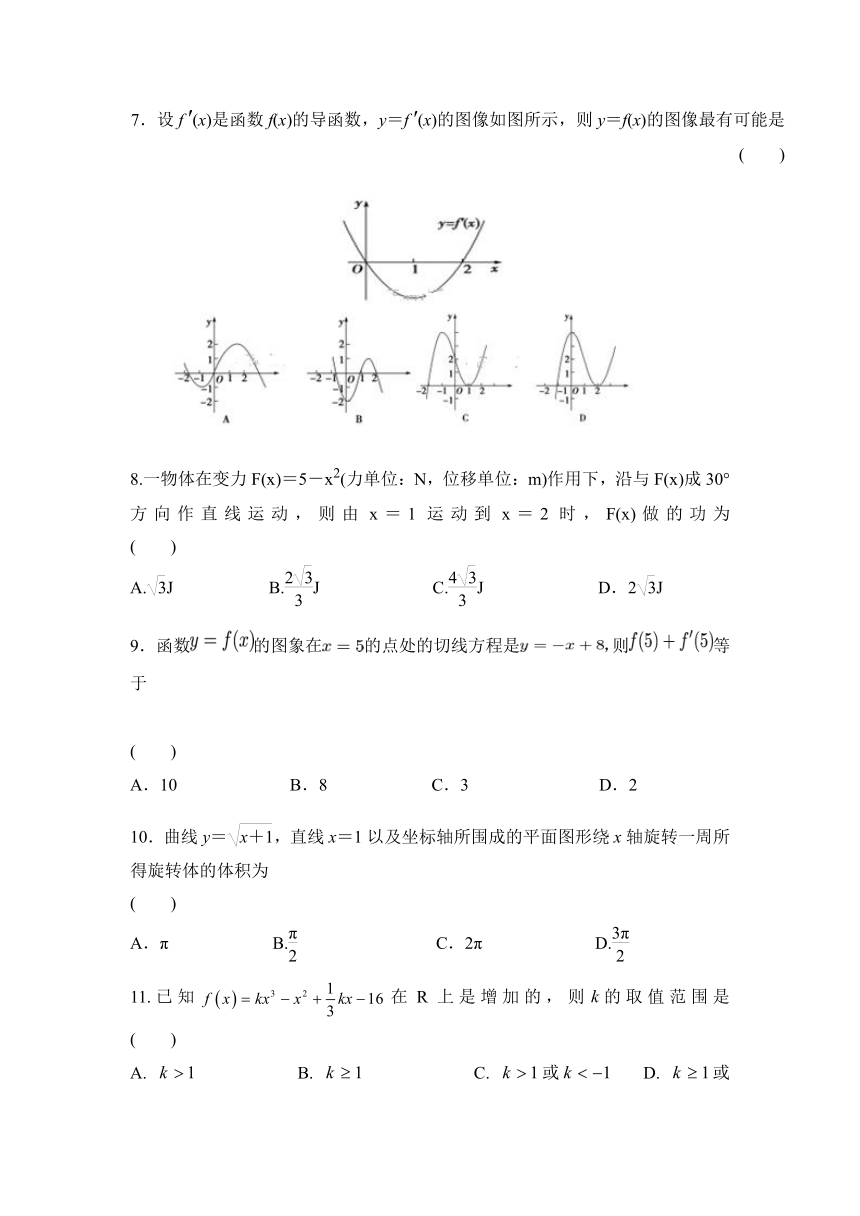
7.设f ′(x)是函数f(x)的导函数,y=f ′(x)的图像如图所示,则y=f(x)的图像最有可能是 ( )
8.一物体在变力F(x)=5-x2(力单位:N,位移单位:m)作用下,沿与F(x)成30°方向作直线运动,则由x=1运动到x=2时,F(x)做的功为 ( )
A.J B.J C.J D.2J
函数的图象在的点处的切线方程是,则等于
( )?
A.10 B.8 C.3 D.2
10.曲线y=,直线x=1以及坐标轴所围成的平面图形绕x轴旋转一周所得旋转体的体积为 ( )
A.π B. C.2π D.
11.已知在R上是增加的,则的取值范围是 ( )
A. B. C. 或 D. 或
12.是定义在上的非负可导函数,且满足,对任意正数a,b,若,则必有 ( )?
A. B. C. D.
第Ⅱ卷 (非选择题90分)
二、填空题(共4小题,每小题5分,共20分)
13.一个物体的运动方程为s=1-t+t2,其中s的单位是米,t的单位是秒,那么物体在3秒末的瞬时速度是_______________.
14.观察下列等式:13+23=(1+2)2,13+23+33=(1+2+3)2,13+23+33+43=(1+2+3+4)2,…,根据上述规律第5个等式为 .
15.求直线与曲线所围成的平面图形的面积为 .
16.设动直线x=m与函数f(x)=x2,g(x)=lnx的图像分别交于M,N,则|MN|的最小值为 _________
三、解答题(共5小题,共70分)
(本小题满分10分)证明:
18.(本小题满分10分)当实数m为何值时,
(1)为纯虚数;????
(2)为实数;
(3)对应的点在复平面内的第二象限内.
??
19.(本小题满分12分)已知数列满足,.
(1)计算,,,的值;
(2)根据以上计算结果猜想的通项公式,并用数学归纳法证明你的猜想.
20.(本小题满分12分)已知函数f(x)=-x3+3x2+9x+a.
(1)求f(x)的单调区间;
(2)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
21.(本小题满分12分)
某种型号的汽车在匀速行驶中每小时的耗油量(升)关于行驶速度(km/h)的函数解析式可以表示为 ,
已知甲、乙两地相距100km .
(1)当汽车以40km/h的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
22.(本小题满分14分)已知f(x)=ax3+bx2+cx在区间[0,1]上是增函数,在区间(-∞,0]与[1,+∞)上是减函数,且f′=.
(1)求f(x)的解析式;
(2)若在区间上恒有成立,求m的取值范围.
高二第一次质量检测数学答案(理科)
选择题(每小题5分,共60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A B B A C C D C D D B C
填空题(每小题5分,共20分)
5米/秒
16、
解答题(5小题,共70分)
(10分)
证明:要证明
只需证明
只需证明
即证明
即证明42>40,这显然成立,则原不等式得证。
(10分)
解:由,解得,当时,复数z为纯虚数;
由,得或,当或时,复数z为实数;
由,解得,当时,复数z对应的点在第二象限内.
19.(本小题满分12分)
解:(1)由和,得
,,
,. (4分)
(2)由以上结果猜测: (6分)
用数学归纳法证明如下:
(Ⅰ)当时 ,左边,右边,等式成立. (8分)
(Ⅱ)假设当时,命题成立,即成立.
那么,当时,
这就是说,当时等式成立.
由(Ⅰ)和(Ⅱ),可知猜测对于任意正整数都成立.(12分)
20.(12分)
解:(1)f′(x)=-3x2+6x+9,令f′(x)<0,解得x<-1或x>3,
∴函数f(x)的单调减区是为(-∞,-1),(3,+∞).
令f′(x)>0,解得-1∴函数f(x)的单调递增区间为(-1,3).
(2)∵f(-2)=8+12-18+a=2+a,f(2)=-8+12+18+a=22+a,
∴f(2)>f(-2),
∵f(x)在(-1,3)上f′(x)>0,∴f(x)在[-1,2]上单调递增,
又由于f(x)在[-2,-1]上单调递减,
∴f(2)和f(-1)分别是f(x)在区间[-1,2]上的最大值和最小值,
∴22+a=20,则得a=-2.
f(x)=-x3+3x2+9x-2,∴f(-1)=1+3-9-2=-7,
即函数f(x)在区间[-2,2]上的最小值为-7.
21.(本小题满分12分)
解: (1)当km/h时,汽车从甲地到乙地行驶了h
要耗油(升)
(2)当速度为km/h,汽车从甲地到乙地行驶了h,耗油量为升,依题意得
()
令,得
当时,,是减函数
当时,,是增函数
∴当时,取得极小值:
(升)
因此,当汽车以80 km/h的速度匀速行驶时,从甲地到乙地耗油量少,最少为11.25升。
22.(本小题满分14分)解:(1)由f(x)=ax3+bx2+cx,得f′(x)=3ax2+2bx+c.又由f(x)在区间[0,1]上是增函数,在区间(-∞,0]与[1,+∞)上是减函数,可知x=0和x=1是f′(x)=0的解,∴即解得
∴f′(x)=3ax2-3ax.又由f′=,得f′=-=,∴a=-2,
即f(x)=-2x3+3x2.
(2)由[1,3]上恒有f(x)≤mx成立,得恒成立,所以m的取值范围
数学(理)试题
第Ⅰ卷(选择题 共60分)
选择题(本大题共12小题,每小题5分,共60分)
1.复数在复平面上对应的点位于 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2.用反证法证明命题:“若能被5整除,则中至少有一个能被5整除”,那么假设的内容是 ( )
A. 都能被5整除 B. 都不能被5整除
C. 有一个能被5整除 D. 有一个不能被5整除
3.用数学归纳法证明时,第一步应验证不等式 ( )
A. B. C. D.
4.已知函数在点处的切线方程是 ( )
A. B.
C. D.
5.下列值等于1的是 ( )
A. B. C. D.
6.已知函数 ( )
A.0 B.﹣2 C.2e﹣3 D.e﹣3
7.设f ′(x)是函数f(x)的导函数,y=f ′(x)的图像如图所示,则y=f(x)的图像最有可能是 ( )
8.一物体在变力F(x)=5-x2(力单位:N,位移单位:m)作用下,沿与F(x)成30°方向作直线运动,则由x=1运动到x=2时,F(x)做的功为 ( )
A.J B.J C.J D.2J
函数的图象在的点处的切线方程是,则等于
( )?
A.10 B.8 C.3 D.2
10.曲线y=,直线x=1以及坐标轴所围成的平面图形绕x轴旋转一周所得旋转体的体积为 ( )
A.π B. C.2π D.
11.已知在R上是增加的,则的取值范围是 ( )
A. B. C. 或 D. 或
12.是定义在上的非负可导函数,且满足,对任意正数a,b,若,则必有 ( )?
A. B. C. D.
第Ⅱ卷 (非选择题90分)
二、填空题(共4小题,每小题5分,共20分)
13.一个物体的运动方程为s=1-t+t2,其中s的单位是米,t的单位是秒,那么物体在3秒末的瞬时速度是_______________.
14.观察下列等式:13+23=(1+2)2,13+23+33=(1+2+3)2,13+23+33+43=(1+2+3+4)2,…,根据上述规律第5个等式为 .
15.求直线与曲线所围成的平面图形的面积为 .
16.设动直线x=m与函数f(x)=x2,g(x)=lnx的图像分别交于M,N,则|MN|的最小值为 _________
三、解答题(共5小题,共70分)
(本小题满分10分)证明:
18.(本小题满分10分)当实数m为何值时,
(1)为纯虚数;????
(2)为实数;
(3)对应的点在复平面内的第二象限内.
??
19.(本小题满分12分)已知数列满足,.
(1)计算,,,的值;
(2)根据以上计算结果猜想的通项公式,并用数学归纳法证明你的猜想.
20.(本小题满分12分)已知函数f(x)=-x3+3x2+9x+a.
(1)求f(x)的单调区间;
(2)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
21.(本小题满分12分)
某种型号的汽车在匀速行驶中每小时的耗油量(升)关于行驶速度(km/h)的函数解析式可以表示为 ,
已知甲、乙两地相距100km .
(1)当汽车以40km/h的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
22.(本小题满分14分)已知f(x)=ax3+bx2+cx在区间[0,1]上是增函数,在区间(-∞,0]与[1,+∞)上是减函数,且f′=.
(1)求f(x)的解析式;
(2)若在区间上恒有成立,求m的取值范围.
高二第一次质量检测数学答案(理科)
选择题(每小题5分,共60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A B B A C C D C D D B C
填空题(每小题5分,共20分)
5米/秒
16、
解答题(5小题,共70分)
(10分)
证明:要证明
只需证明
只需证明
即证明
即证明42>40,这显然成立,则原不等式得证。
(10分)
解:由,解得,当时,复数z为纯虚数;
由,得或,当或时,复数z为实数;
由,解得,当时,复数z对应的点在第二象限内.
19.(本小题满分12分)
解:(1)由和,得
,,
,. (4分)
(2)由以上结果猜测: (6分)
用数学归纳法证明如下:
(Ⅰ)当时 ,左边,右边,等式成立. (8分)
(Ⅱ)假设当时,命题成立,即成立.
那么,当时,
这就是说,当时等式成立.
由(Ⅰ)和(Ⅱ),可知猜测对于任意正整数都成立.(12分)
20.(12分)
解:(1)f′(x)=-3x2+6x+9,令f′(x)<0,解得x<-1或x>3,
∴函数f(x)的单调减区是为(-∞,-1),(3,+∞).
令f′(x)>0,解得-1
(2)∵f(-2)=8+12-18+a=2+a,f(2)=-8+12+18+a=22+a,
∴f(2)>f(-2),
∵f(x)在(-1,3)上f′(x)>0,∴f(x)在[-1,2]上单调递增,
又由于f(x)在[-2,-1]上单调递减,
∴f(2)和f(-1)分别是f(x)在区间[-1,2]上的最大值和最小值,
∴22+a=20,则得a=-2.
f(x)=-x3+3x2+9x-2,∴f(-1)=1+3-9-2=-7,
即函数f(x)在区间[-2,2]上的最小值为-7.
21.(本小题满分12分)
解: (1)当km/h时,汽车从甲地到乙地行驶了h
要耗油(升)
(2)当速度为km/h,汽车从甲地到乙地行驶了h,耗油量为升,依题意得
()
令,得
当时,,是减函数
当时,,是增函数
∴当时,取得极小值:
(升)
因此,当汽车以80 km/h的速度匀速行驶时,从甲地到乙地耗油量少,最少为11.25升。
22.(本小题满分14分)解:(1)由f(x)=ax3+bx2+cx,得f′(x)=3ax2+2bx+c.又由f(x)在区间[0,1]上是增函数,在区间(-∞,0]与[1,+∞)上是减函数,可知x=0和x=1是f′(x)=0的解,∴即解得
∴f′(x)=3ax2-3ax.又由f′=,得f′=-=,∴a=-2,
即f(x)=-2x3+3x2.
(2)由[1,3]上恒有f(x)≤mx成立,得恒成立,所以m的取值范围
同课章节目录
