10.4平行线的判定（一）导学案

10.4平行线的判定（一）导学案
一．复习旧知，导入新课 .
平行线有哪些性质？
二．学习目标和重点、难点。
学习目标
1. 经历观察、推理、思考等活动探索平行线的判定方法。
2.灵活运用判定定理解决实际问题。
3.通过活动培养学生的推理意识和语言表达能力。
重点：平行线判定方法的推理过程和平行线判定方法的灵活运用。
难点：使用符号语言进行正确推理。
三．探究新知
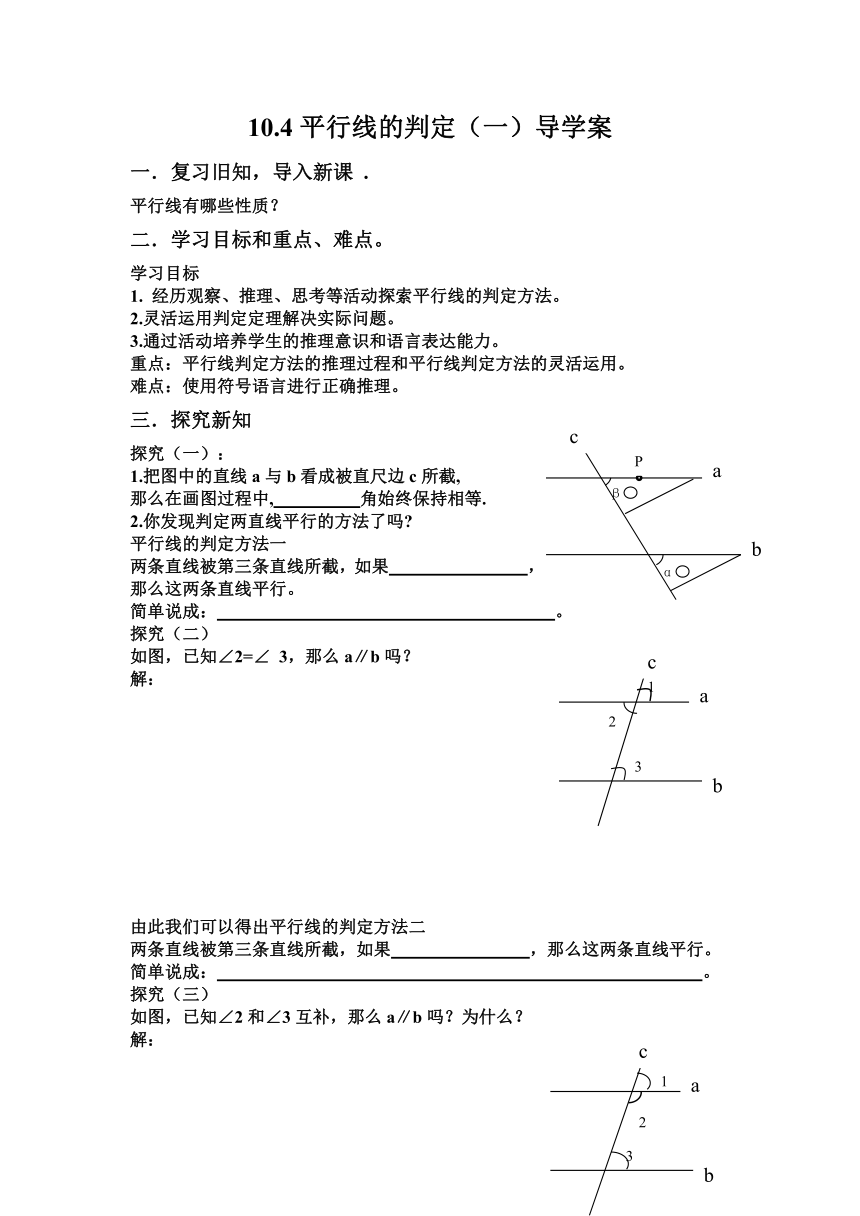
探究（一）：
1.把图中的直线a与b看成被直尺边c所截,
那么在画图过程中, 角始终保持相等.
2.你发现判定两直线平行的方法了吗
平行线的判定方法一
两条直线被第三条直线所截，如果 ，
那么这两条直线平行。
简单说成： 。
探究（二）
如图，已知∠2=∠ 3，那么a∥b吗？
解：
由此我们可以得出平行线的判定方法二
两条直线被第三条直线所截，如果 ，那么这两条直线平行。
简单说成： 。
探究（三）
如图，已知∠2和∠3互补，那么a∥b吗？为什么？
解：
由此我们可以得出平行线的判定方法三
两条直线被第三条直线所截，如果 ，那么这两条直线平行.
简单说成： .
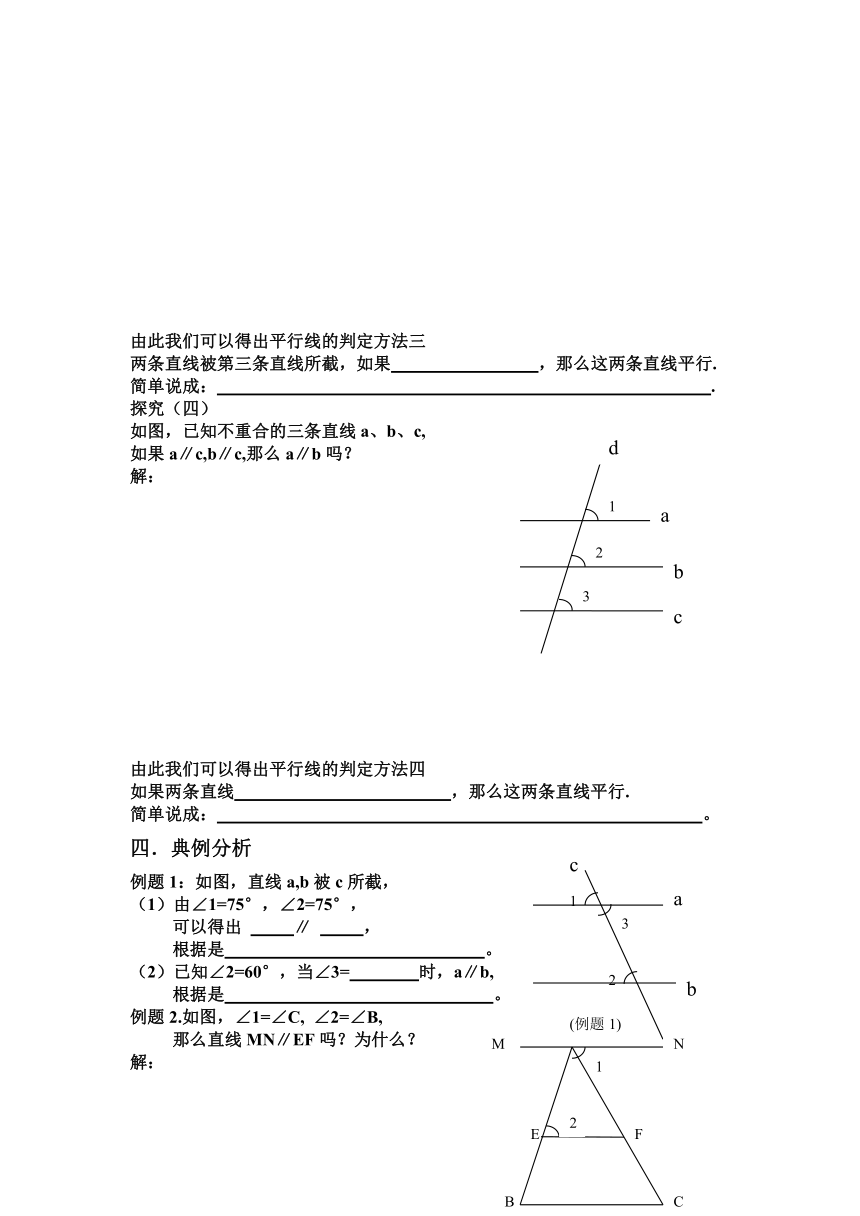
探究（四）
如图，已知不重合的三条直线a、b、c,
如果a∥c,b∥c,那么a∥b吗？
解：
由此我们可以得出平行线的判定方法四
如果两条直线 ，那么这两条直线平行.
简单说成： 。
四．典例分析
例题1：如图，直线a,b被c所截，
（1）由∠1=75°，∠2=75°，
可以得出 ∥ ，
根据是 。
（2）已知∠2=60°，当∠3= 时，a∥b,
根据是 。
例题2.如图，∠1=∠C, ∠2=∠B,
那么直线MN∥EF吗？为什么？
解：
(例题2)
五．巩固提高
1.如图1，BE为AB的延长线，
（1）.因为∠1 =∠2，所以 ∥ ，
根据是 。
（2）.因为∠A=∠4 ，所以 ∥ ， （图1）
根据是 。
（3）.因为∠A+∠ABC=180 °，所以 ∥ ，
根据是 。
2.如图,下列条件中，
不能判断直线a∥b的是（ ）.
A.∠3=∠4 B.∠1=∠2
C.∠2=∠3 D.∠3+∠5=180°
3.如图，已知∠1=70°，∠2=70°
∠3=80°，则∠4=（ ）
A.70° B.140° C.80° D.100°
4.如图，是由四条线段构成的“鱼”形图案，
已知∠1=60°，∠2=60°，∠3=120°，
找出图中平行的线，并说明理由。
六．课堂小结：通过本节课的学习你有什么收获？
七．作业
必做题：P39 A组第4题，第7 题。
选做题：P39 B组第2题。
α
β
c
a
b
P
2
3
1
c
a
b
2
1
3
c
a
b
3
2
1
d
a
b
c
c
(例题1)
2
3
1
a
b
C
B
1
F
E
M
N
2
E
B
A
C
D
2
4
1
1
3
4
2
a
b
5
4
3
2
1
a
b
B
C
D
6
5
4
3
2
1
A