8.6.3平面与平面垂直(32张PPT)
文档属性
| 名称 | 8.6.3平面与平面垂直(32张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-04 00:00:00 | ||
图片预览





文档简介
09人教A版 必修二
8.6 空间直线、平面的垂直
8. 6. 3 平面与平面垂直
像研究直线与平面垂直一样,我们首先应给出平面与平面垂直的定义.那么,该如何定义呢?不妨回顾一下直线与平面垂直、 直线与直线垂直的定义过程.
在定义直线与平面垂直时,我们利用了直线与直线的垂直.所以,直线与直线垂直是研究直线、平面垂直问题的基础.
在平面几何中,我们先定义了角的概念,利用角刻画两条相交直线的位置关系,进而研究直线与直线互相垂直这种特殊情况.类似地,我们需要先引进二面角的概念,用以刻画两个相交平面的位置关系,进而研究两个平面互相垂直.
l
A
B
P
Q
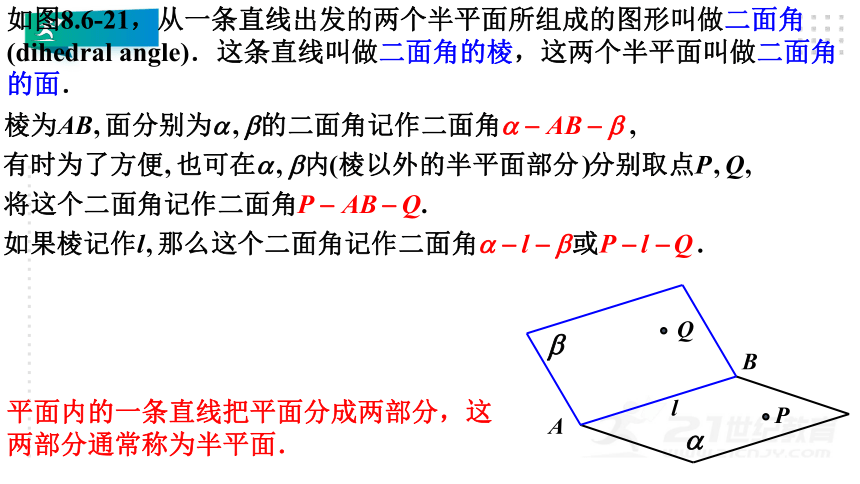
如图8.6-21,从一条直线出发的两个半平面所组成的图形叫做二面角(dihedral angle).这条直线叫做二面角的棱,这两个半平面叫做二面角的面.
平面内的一条直线把平面分成两部分,这两部分通常称为半平面.
l
?
?
A
B
?
?
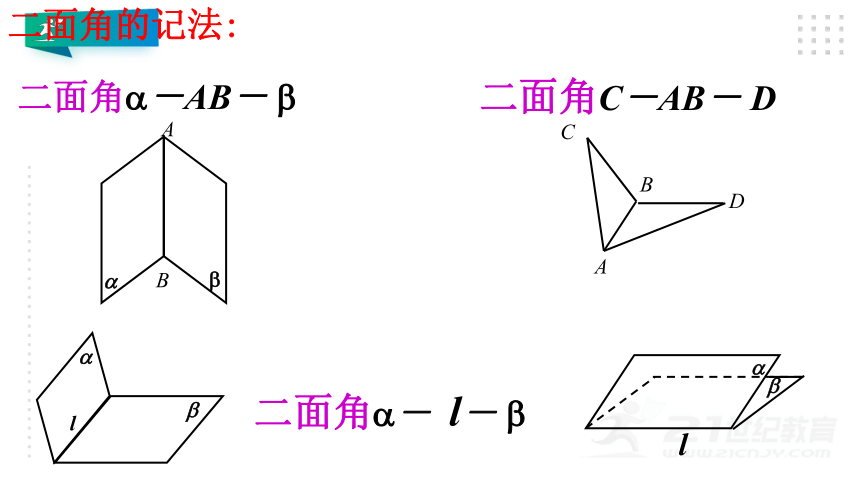
二面角?-AB- ?
?
?
l
二面角?- l- ?
二面角C-AB- D
A
B
C
D
5
二面角的记法:
图8.6-22
思考
如图8.6-22,在日常生活中,我们常说“把门开大一些”,
是指哪个角大一些?受此启发,
你认为应该怎样刻画二面角的大小呢?
l
A
B
O
图8.6-23
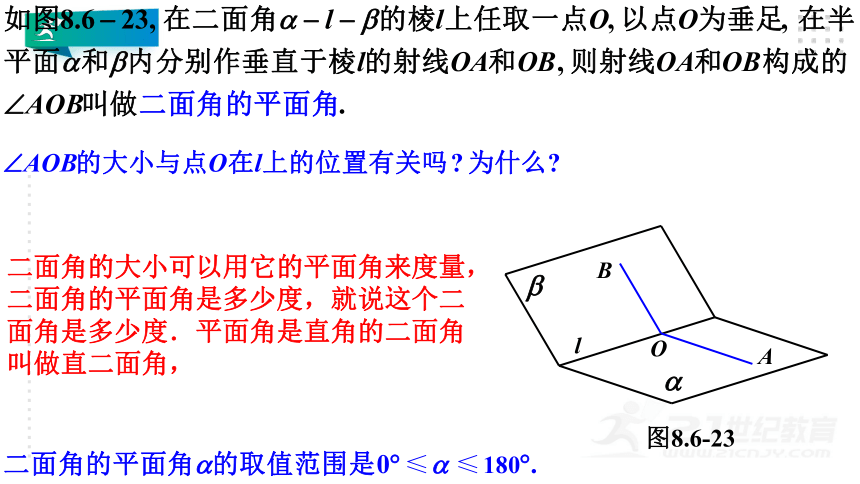
二面角的大小可以用它的平面角来度量,二面角的平面角是多少度,就说这个二面角是多少度.平面角是直角的二面角叫做直二面角,
观察
教室相邻的两个墙面与地面可以构成几个二面角?分别指出构成这些二面角的面、棱、平面角及其度数.
教室里的墙面所在平面与地面所在平面相交,它们所成的二面角是直二面角,我们常说墙面直立于地面上.
一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.
图8.6-24
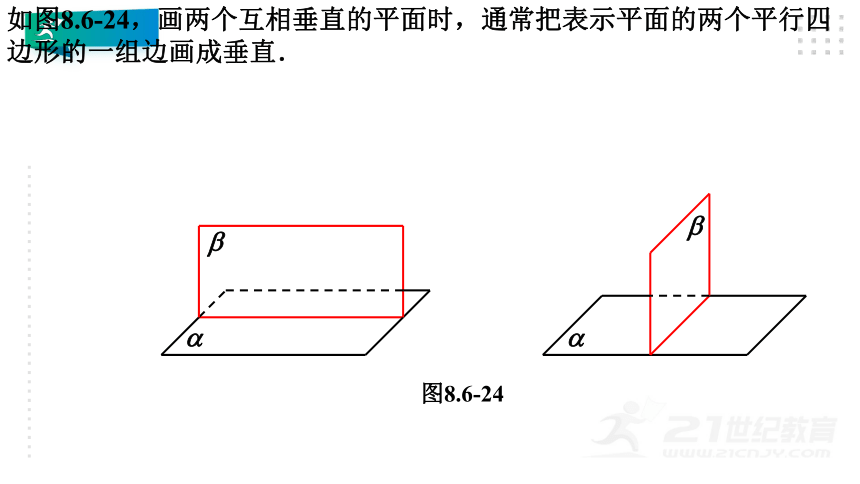
如图8.6-24,画两个互相垂直的平面时,通常把表示平面的两个平行四边形的一组边画成垂直.
在明确了两个平面互相垂直的定义的基础上,我们研究两个平面垂直的判定和性质.先研究平面与平面垂直的判定.
观察
如图8.6-25,建筑工人在砌墙时,常用铅锤来检测所砌的墙面与地面是否垂直.如果系有铅锤的细线紧贴墙面,工人师傅就认为墙面垂直于地面,否则他就认为墙面不垂直于地面.
这种方法说明了什么道理?
A
B
C
D
图8.6-26
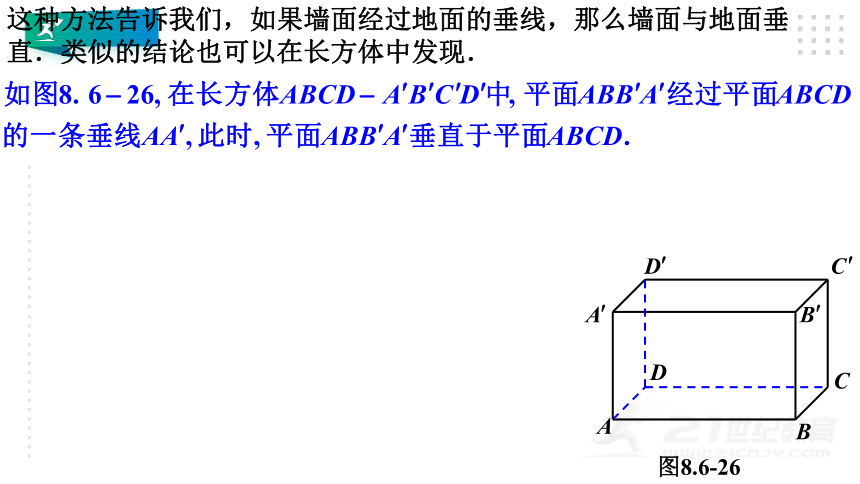
这种方法告诉我们,如果墙面经过地面的垂线,那么墙面与地面垂直.类似的结论也可以在长方体中发现.
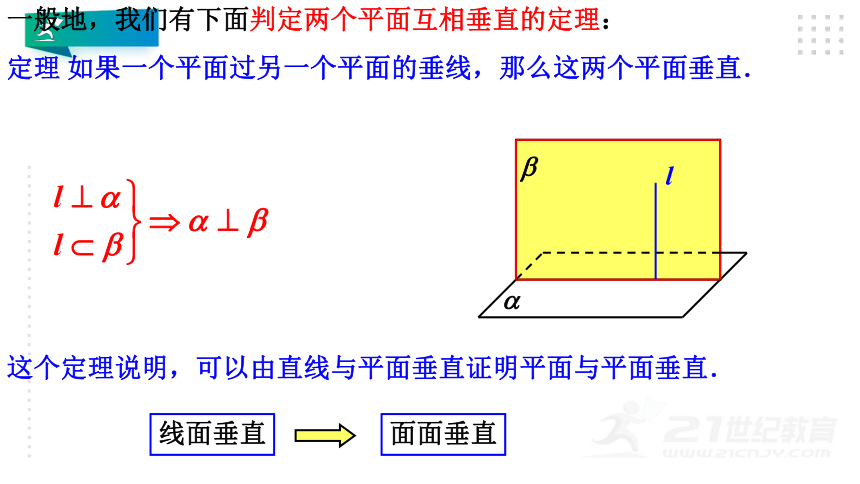
一般地,我们有下面判定两个平面互相垂直的定理:
定理 如果一个平面过另一个平面的垂线,那么这两个平面垂直.
l
这个定理说明,可以由直线与平面垂直证明平面与平面垂直.
线面垂直
面面垂直
A
B
C
D
图8.6-27
P
A
B
O
C
图8.6-28
分析:要证明两个平面垂直,根据两个平面垂直的判定定理,只需证明其中一个平面内的一条直线垂直于另一个平面.而由直线和平面垂直的判定定理,还需证明这条直线和另一个平面内的两条相交直线垂直.
P
A
B
O
C
图8.6-28
(第1题)
练习(第158页)
1.如图,检查工件的相邻两个(平)面是否垂直时,只要用曲尺的一边紧靠在工件的一个面上,另一边在工件的另一个面上转动,观察尺边和这个面是否密合就可以了.这是为什么?
当曲尺的另一边在工件的另一个面上转动时,如果和另一个面密合,曲尺紧靠工件一个面的边就与另一个面内无 数条相交直线都垂直,从而这边就与另一个面垂直. 同时, 这边紧靠工件的一个面,可看成这边在这个面内,故这两个面垂直.
a
b
a
b
a
D
A
B
C
D
B
C
A
D
a
b
图8.6-29
下面我们研究平面与平面垂直的性质,也就是在两个平面互相垂直的条件下,能推出哪些结论.
如果两个平面互相垂直,根据已有的研究经验,我们可以先研究其中一个平面内的直线与另一个平面具有什么位置关系.
a
b
图8.6-30
c
A
由此我们得到平面与平面垂直的性质定理:
定理两个平面垂直,如果一个平面内有一直线垂直于这两个平面的交线,那么这条直线与另一个平面垂直.
a
b
图8.6-30
c
A
这个定理说明,由平面与平面垂直可以得到直线与平面垂直.
面面垂直
线面垂直
这个性质定理可以用于解决现实生活中的问题.例如,装修房子时,要在墙壁上画出与地面垂直的直线,只需在墙面上画出地面与墙面的交线的垂线即可.
我们知道,过一点只能作一条直线与已知平面垂直.因此,如果过一点有两条直线与平面垂直,那么这两条直线重合.
P
b
c
a
P
b
c
a
图8.6-31
b
a
图8.6-32
对于两个平面互相垂直的性质,我们探究了一个平面内的直线与另一个平面的特殊位置关系如果直线不在两个平面内,或者把直线换成平面,你又能得到哪些结论?
下面的例子就是其中的一些结果.
P
A
C
B
E
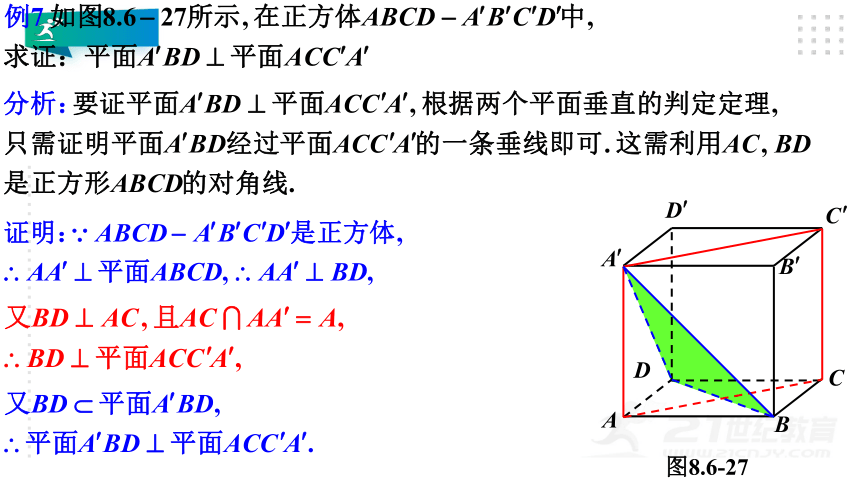
例10 如图,已知PA⊥平面ABC,平面PAB⊥平面PBC,求证: BC⊥平面PAB.
分析:要证明BC⊥平面PAB,需证明BC垂直于平面PAB内的两条相交直线.由已知条件易得BC⊥PA.再利用平面PAB⊥平面PBC,过点A作PB的垂线AE,由两个平面垂直的性质可得BC⊥AE.
直线与直线垂直
直线与平面垂直
平面与平面垂直
判定
判定
性质
从本节的讨论可以看到,由直线与直线垂直可以判定直线与平面垂直;由直线与平面垂直的定义可以得到直线与直线垂直;由直线与平面垂直可以判定平面与平面垂直;而由平面与平面垂直的性质可以得到直线与平面垂直.这进一步揭示了直线、平面之间的位置关系可以相互转化.
练习(第161页)
a
b
a
b
×
√
√
①错误,若一平面内的已知直线垂直于另一个平面内的任意直线,则已知直线就垂直于另一平面,而一个平面内的直线与另一平面还存在平行和相交两种情况.
②正确,在另一平面内存在无数条与两平面的交线垂直的直线,而这些直线都与第一个平面的已知直线垂直.
③错误(参考①的分析) .
④正确(参考性质定理) .故况B
B
B
A
B
a
8.6 空间直线、平面的垂直
8. 6. 3 平面与平面垂直
像研究直线与平面垂直一样,我们首先应给出平面与平面垂直的定义.那么,该如何定义呢?不妨回顾一下直线与平面垂直、 直线与直线垂直的定义过程.
在定义直线与平面垂直时,我们利用了直线与直线的垂直.所以,直线与直线垂直是研究直线、平面垂直问题的基础.
在平面几何中,我们先定义了角的概念,利用角刻画两条相交直线的位置关系,进而研究直线与直线互相垂直这种特殊情况.类似地,我们需要先引进二面角的概念,用以刻画两个相交平面的位置关系,进而研究两个平面互相垂直.
l
A
B
P
Q
如图8.6-21,从一条直线出发的两个半平面所组成的图形叫做二面角(dihedral angle).这条直线叫做二面角的棱,这两个半平面叫做二面角的面.
平面内的一条直线把平面分成两部分,这两部分通常称为半平面.
l
?
?
A
B
?
?
二面角?-AB- ?
?
?
l
二面角?- l- ?
二面角C-AB- D
A
B
C
D
5
二面角的记法:
图8.6-22
思考
如图8.6-22,在日常生活中,我们常说“把门开大一些”,
是指哪个角大一些?受此启发,
你认为应该怎样刻画二面角的大小呢?
l
A
B
O
图8.6-23
二面角的大小可以用它的平面角来度量,二面角的平面角是多少度,就说这个二面角是多少度.平面角是直角的二面角叫做直二面角,
观察
教室相邻的两个墙面与地面可以构成几个二面角?分别指出构成这些二面角的面、棱、平面角及其度数.
教室里的墙面所在平面与地面所在平面相交,它们所成的二面角是直二面角,我们常说墙面直立于地面上.
一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.
图8.6-24
如图8.6-24,画两个互相垂直的平面时,通常把表示平面的两个平行四边形的一组边画成垂直.
在明确了两个平面互相垂直的定义的基础上,我们研究两个平面垂直的判定和性质.先研究平面与平面垂直的判定.
观察
如图8.6-25,建筑工人在砌墙时,常用铅锤来检测所砌的墙面与地面是否垂直.如果系有铅锤的细线紧贴墙面,工人师傅就认为墙面垂直于地面,否则他就认为墙面不垂直于地面.
这种方法说明了什么道理?
A
B
C
D
图8.6-26
这种方法告诉我们,如果墙面经过地面的垂线,那么墙面与地面垂直.类似的结论也可以在长方体中发现.
一般地,我们有下面判定两个平面互相垂直的定理:
定理 如果一个平面过另一个平面的垂线,那么这两个平面垂直.
l
这个定理说明,可以由直线与平面垂直证明平面与平面垂直.
线面垂直
面面垂直
A
B
C
D
图8.6-27
P
A
B
O
C
图8.6-28
分析:要证明两个平面垂直,根据两个平面垂直的判定定理,只需证明其中一个平面内的一条直线垂直于另一个平面.而由直线和平面垂直的判定定理,还需证明这条直线和另一个平面内的两条相交直线垂直.
P
A
B
O
C
图8.6-28
(第1题)
练习(第158页)
1.如图,检查工件的相邻两个(平)面是否垂直时,只要用曲尺的一边紧靠在工件的一个面上,另一边在工件的另一个面上转动,观察尺边和这个面是否密合就可以了.这是为什么?
当曲尺的另一边在工件的另一个面上转动时,如果和另一个面密合,曲尺紧靠工件一个面的边就与另一个面内无 数条相交直线都垂直,从而这边就与另一个面垂直. 同时, 这边紧靠工件的一个面,可看成这边在这个面内,故这两个面垂直.
a
b
a
b
a
D
A
B
C
D
B
C
A
D
a
b
图8.6-29
下面我们研究平面与平面垂直的性质,也就是在两个平面互相垂直的条件下,能推出哪些结论.
如果两个平面互相垂直,根据已有的研究经验,我们可以先研究其中一个平面内的直线与另一个平面具有什么位置关系.
a
b
图8.6-30
c
A
由此我们得到平面与平面垂直的性质定理:
定理两个平面垂直,如果一个平面内有一直线垂直于这两个平面的交线,那么这条直线与另一个平面垂直.
a
b
图8.6-30
c
A
这个定理说明,由平面与平面垂直可以得到直线与平面垂直.
面面垂直
线面垂直
这个性质定理可以用于解决现实生活中的问题.例如,装修房子时,要在墙壁上画出与地面垂直的直线,只需在墙面上画出地面与墙面的交线的垂线即可.
我们知道,过一点只能作一条直线与已知平面垂直.因此,如果过一点有两条直线与平面垂直,那么这两条直线重合.
P
b
c
a
P
b
c
a
图8.6-31
b
a
图8.6-32
对于两个平面互相垂直的性质,我们探究了一个平面内的直线与另一个平面的特殊位置关系如果直线不在两个平面内,或者把直线换成平面,你又能得到哪些结论?
下面的例子就是其中的一些结果.
P
A
C
B
E
例10 如图,已知PA⊥平面ABC,平面PAB⊥平面PBC,求证: BC⊥平面PAB.
分析:要证明BC⊥平面PAB,需证明BC垂直于平面PAB内的两条相交直线.由已知条件易得BC⊥PA.再利用平面PAB⊥平面PBC,过点A作PB的垂线AE,由两个平面垂直的性质可得BC⊥AE.
直线与直线垂直
直线与平面垂直
平面与平面垂直
判定
判定
性质
从本节的讨论可以看到,由直线与直线垂直可以判定直线与平面垂直;由直线与平面垂直的定义可以得到直线与直线垂直;由直线与平面垂直可以判定平面与平面垂直;而由平面与平面垂直的性质可以得到直线与平面垂直.这进一步揭示了直线、平面之间的位置关系可以相互转化.
练习(第161页)
a
b
a
b
×
√
√
①错误,若一平面内的已知直线垂直于另一个平面内的任意直线,则已知直线就垂直于另一平面,而一个平面内的直线与另一平面还存在平行和相交两种情况.
②正确,在另一平面内存在无数条与两平面的交线垂直的直线,而这些直线都与第一个平面的已知直线垂直.
③错误(参考①的分析) .
④正确(参考性质定理) .故况B
B
B
A
B
a
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
