习题8.6及复习参考题8(53张PPT)
文档属性
| 名称 | 习题8.6及复习参考题8(53张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-04 00:00:00 | ||
图片预览





文档简介
09人教A版 必修二
8.6 空间直线、平面的垂直
习题8.6(第162页)
复习参考题8(第169页)
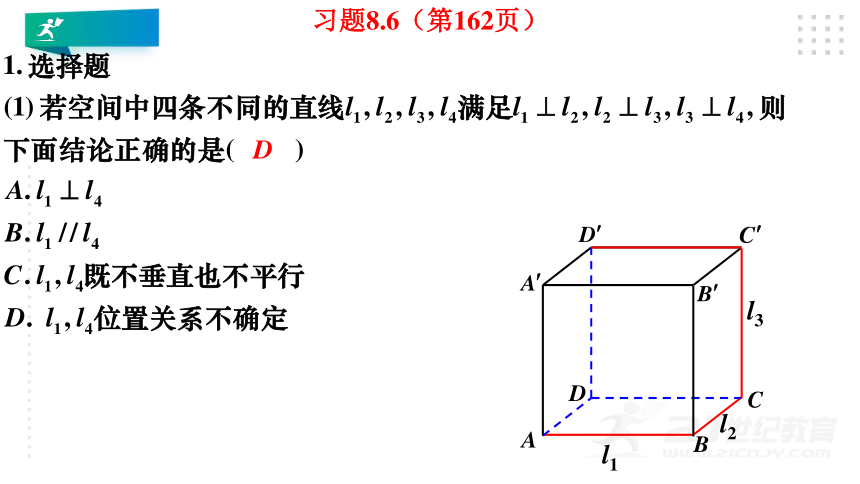
习题8.6(第162页)
A
B
C
D
l1
l2
l3
D
A
C
2.判断下列命题是否正确,正确的在括号内画“√”,错误的“×”.
(1)过平面外一点,有且只有一条直线与这个平面垂直. ( )
(2)过平面外一点,有且只有一条直线与这个平面平行. ( )
(3)过直线外一点,有且只有一个平面与这条直线垂直. ( )
(4)过直线外一点,有且只有一个平面与这条直线平行. ( )
(5)过直线外一点,有且只有一条直线与这条直线平行. ( )
√
×
√
×
√
(1)正确.因为另一条直线与这个平面垂直,则另一条直线垂直于这个平面内的任意一条直线.所以另一条直线一定垂直于平面内与已知直线平行的直线.故两条直线垂直.
(2)正确.
(3)错误.比如正方体两个相对的侧面,都垂直于底面,但两侧面平行.
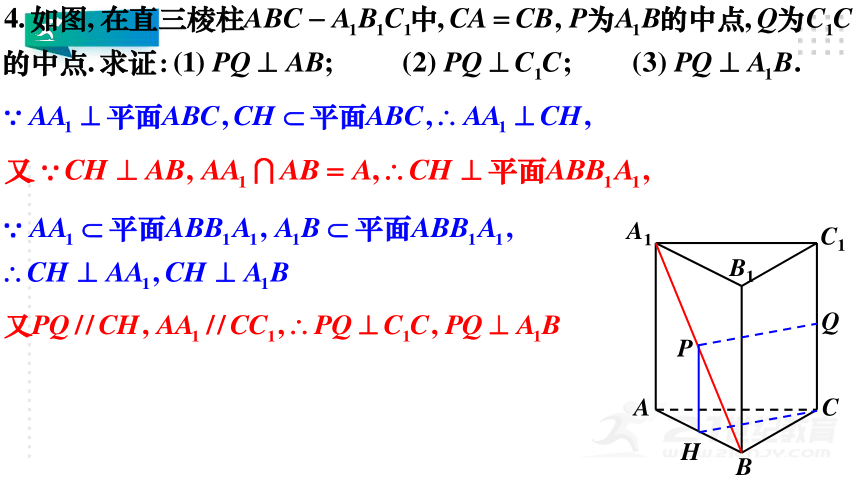
A
A
B
C
P
Q
A1
B1
C1
H
A
B
C
P
Q
A1
B1
C1
H
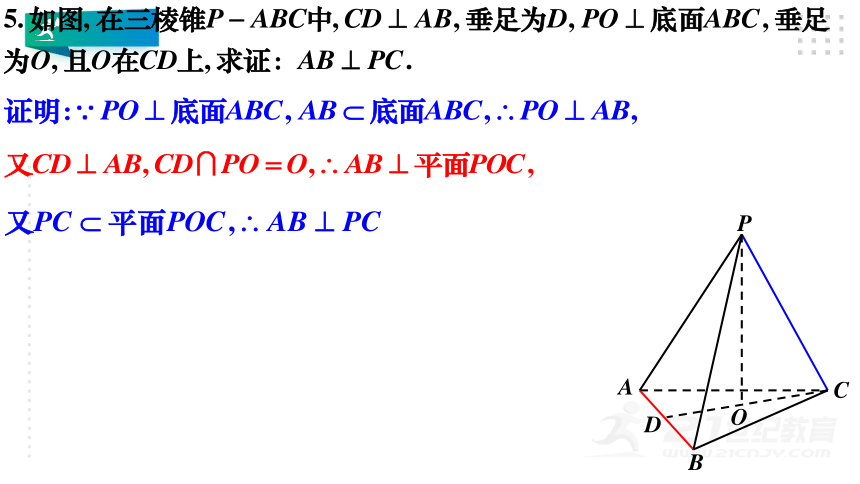
P
A
B
C
O
D
A
B
C
D
V
C
A
B
鳖臑
V
A
B
C
8.求证:如果共点的三条直线两两垂直,那么它们中每两条直线确定的平面也两两垂直.
a
l
b
M
N
c
d
e
m
l
A
B
C
D
A1
B1
C1
D1
P
Q
O
m
n
l
l1
l2
1
2
A
A1
A2
B
B1
B2
a
b
13.求证:两条平行直线与同一个平面所成的角相等.
V
A
B
C
D
O
能.理由如下:
S
D
E
F
G1
G2
G3
S
G
F
E
D
S
D
E
F
G1
G2
G3
S
G
F
E
D
3. 通常我们把三条侧棱两两垂直的三棱锥称作“直角三棱锥”.
a
b
c
16.求证:垂直于两个平行平面中的一个平面的直线也垂直于另一个平面(155页第4题的逆命题).
a
A
B
C
l
m
n
17.求证:三个两两垂直的平面的交线也两两垂直(第8题的逆命题).
所以三条交线两两垂直
V
A
B
C
O
A
B
C
C1
A1
B1
(三垂线定理)
A
B
V
D
E
Q
C
P
A
B
C
D
E
F
复习参考题8(第169页)
1. 从多面体角度去考察棱柱、棱锥、棱台,填写下列表格:
多面体
顶点数V
棱数E
面数F
n棱柱
n棱锥
n棱台
考虑一个多面体,例如正六面体,假定它的面是用橡胶薄膜做成的,如果充以气体,那么它就会连续(不破裂)变形,最后可变为一个球面,象这样,表面经过连续变形可变为球面的多面体,叫做简单多面体
例:欧拉定理在研究化学分子结构中的应用:1996年诺贝尔化学奖授予对发现有重大贡献的三位科学家是由60个原子构成的分子,它是形如足球的多面体这个多面体有60个顶点,以每一个顶点为一端点都有三条棱,面的形状只有五边形和六边形,计算分子中五边形和六边形的数目
A
D
C
B
B1
C1
A1
D1
(1)
A
D
C
E
B
B1
C1
E1
A1
D1
(2)
3.填空题
(1)正方体的棱长扩大到原来的n倍,则其表面积扩大到原来的
倍,体积扩大到原来的 倍;
(2)球的半径扩大到原来的n倍,则其表面积扩大到原来的的 倍,体积扩大到原来的 倍.
相似几何体的表面积之比是相似比的平方,体积之比是相似比的三次方。
5
10
x
4.如图,一块边长为10 cm的正方形铁片上有四块阴影部分.将这些阴影部分裁下来,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,把容器的容积V (单位:cm3) 表示为x (单位:cm)的函数.
A
B
C
D
E
O
F
A
B
C
D
E
O
F
5
10
x
5.三个平面可以将空间分成几个部分?请说明理由.
三个平面可将空间分成4或6或7或8部分,
它们的直观图如图:
O
A
B
C
A
B
C
D
在平行投影法下,两平行直线的投影一般仍平行(投影重合为其特例)
A
B
C
D
A1
B1
C1
D1
E
8. 如图,一块正方体形木料的上底面有一点E.若经过点E在上底面上画一条直线与CE垂直,则应该怎样画?
三垂线定理的应用
A
B
C
P
D
E
A
B
C
D
E
F
F
D
E
A
B
C
D
E
F
F
D
E
A
B
C
D
M
P
Q
O
F
A
B
C
D
M
P
Q
F
A
B
C
D
A1
B1
C1
D1
A
B
C
D
A1
B1
C1
D1
H
A
B
C
D
A1
B1
C1
D1
H
P
A
M
C
B
鳖臑
P
A
M
C
B
D
P
A
M
B
C
D
P
A
M
B
C
D
E
F
作二面角的平面角的方法
注:P点一般是题目中给出的点。
P
A
B
一作二证三计算
a
b
m
a
m
n
l
B
8.6 空间直线、平面的垂直
习题8.6(第162页)
复习参考题8(第169页)
习题8.6(第162页)
A
B
C
D
l1
l2
l3
D
A
C
2.判断下列命题是否正确,正确的在括号内画“√”,错误的“×”.
(1)过平面外一点,有且只有一条直线与这个平面垂直. ( )
(2)过平面外一点,有且只有一条直线与这个平面平行. ( )
(3)过直线外一点,有且只有一个平面与这条直线垂直. ( )
(4)过直线外一点,有且只有一个平面与这条直线平行. ( )
(5)过直线外一点,有且只有一条直线与这条直线平行. ( )
√
×
√
×
√
(1)正确.因为另一条直线与这个平面垂直,则另一条直线垂直于这个平面内的任意一条直线.所以另一条直线一定垂直于平面内与已知直线平行的直线.故两条直线垂直.
(2)正确.
(3)错误.比如正方体两个相对的侧面,都垂直于底面,但两侧面平行.
A
A
B
C
P
Q
A1
B1
C1
H
A
B
C
P
Q
A1
B1
C1
H
P
A
B
C
O
D
A
B
C
D
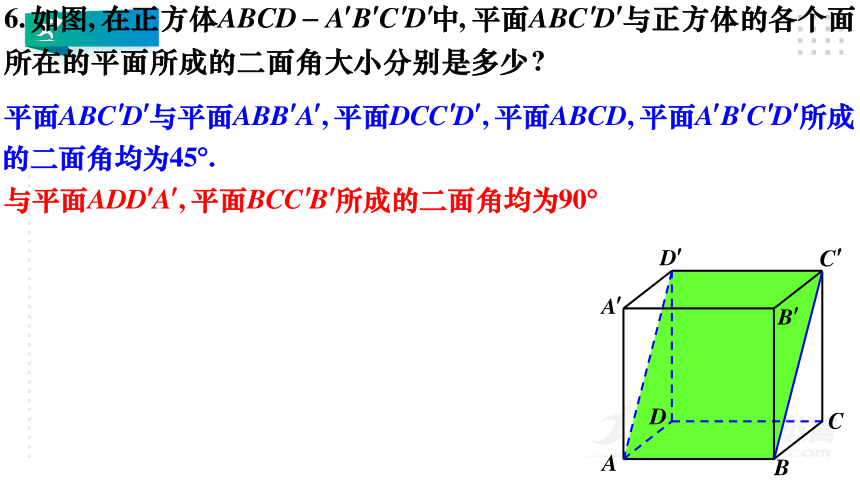
V
C
A
B
鳖臑
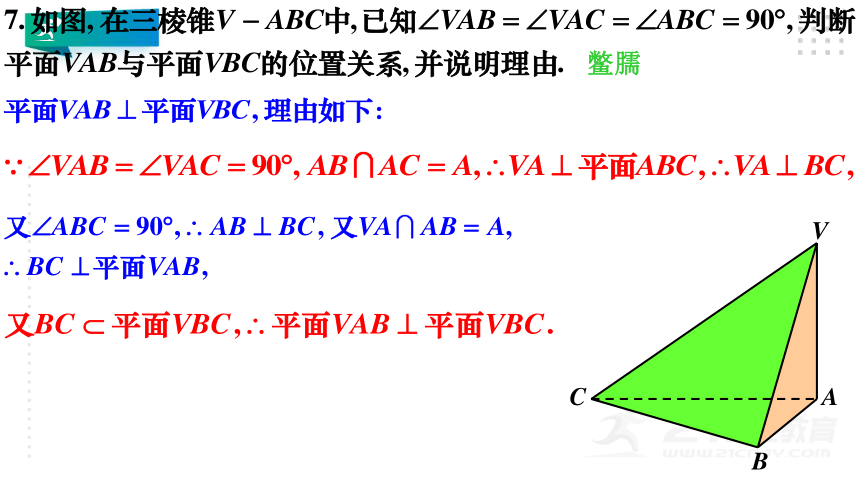
V
A
B
C
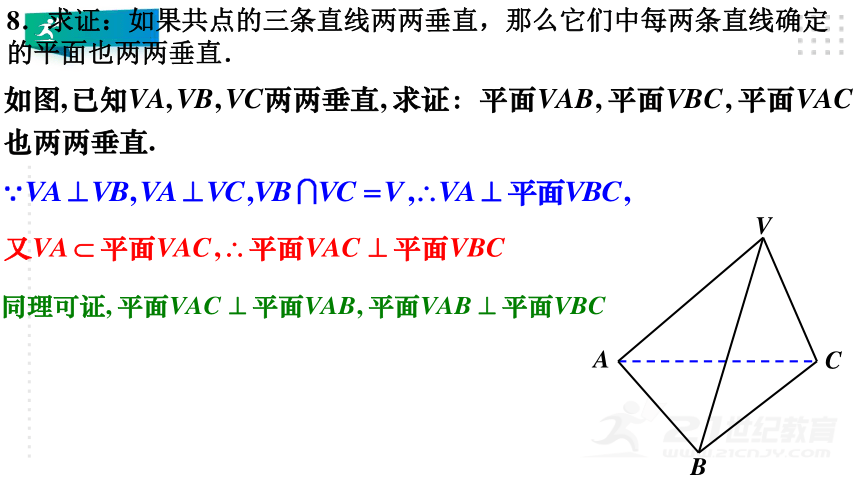
8.求证:如果共点的三条直线两两垂直,那么它们中每两条直线确定的平面也两两垂直.
a
l
b
M
N
c
d
e
m
l
A
B
C
D
A1
B1
C1
D1
P
Q
O
m
n
l
l1
l2
1
2
A
A1
A2
B
B1
B2
a
b
13.求证:两条平行直线与同一个平面所成的角相等.
V
A
B
C
D
O
能.理由如下:
S
D
E
F
G1
G2
G3
S
G
F
E
D
S
D
E
F
G1
G2
G3
S
G
F
E
D
3. 通常我们把三条侧棱两两垂直的三棱锥称作“直角三棱锥”.
a
b
c
16.求证:垂直于两个平行平面中的一个平面的直线也垂直于另一个平面(155页第4题的逆命题).
a
A
B
C
l
m
n
17.求证:三个两两垂直的平面的交线也两两垂直(第8题的逆命题).
所以三条交线两两垂直
V
A
B
C
O
A
B
C
C1
A1
B1
(三垂线定理)
A
B
V
D
E
Q
C
P
A
B
C
D
E
F
复习参考题8(第169页)
1. 从多面体角度去考察棱柱、棱锥、棱台,填写下列表格:
多面体
顶点数V
棱数E
面数F
n棱柱
n棱锥
n棱台
考虑一个多面体,例如正六面体,假定它的面是用橡胶薄膜做成的,如果充以气体,那么它就会连续(不破裂)变形,最后可变为一个球面,象这样,表面经过连续变形可变为球面的多面体,叫做简单多面体
例:欧拉定理在研究化学分子结构中的应用:1996年诺贝尔化学奖授予对发现有重大贡献的三位科学家是由60个原子构成的分子,它是形如足球的多面体这个多面体有60个顶点,以每一个顶点为一端点都有三条棱,面的形状只有五边形和六边形,计算分子中五边形和六边形的数目
A
D
C
B
B1
C1
A1
D1
(1)
A
D
C
E
B
B1
C1
E1
A1
D1
(2)
3.填空题
(1)正方体的棱长扩大到原来的n倍,则其表面积扩大到原来的
倍,体积扩大到原来的 倍;
(2)球的半径扩大到原来的n倍,则其表面积扩大到原来的的 倍,体积扩大到原来的 倍.
相似几何体的表面积之比是相似比的平方,体积之比是相似比的三次方。
5
10
x
4.如图,一块边长为10 cm的正方形铁片上有四块阴影部分.将这些阴影部分裁下来,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,把容器的容积V (单位:cm3) 表示为x (单位:cm)的函数.
A
B
C
D
E
O
F
A
B
C
D
E
O
F
5
10
x
5.三个平面可以将空间分成几个部分?请说明理由.
三个平面可将空间分成4或6或7或8部分,
它们的直观图如图:
O
A
B
C
A
B
C
D
在平行投影法下,两平行直线的投影一般仍平行(投影重合为其特例)
A
B
C
D
A1
B1
C1
D1
E
8. 如图,一块正方体形木料的上底面有一点E.若经过点E在上底面上画一条直线与CE垂直,则应该怎样画?
三垂线定理的应用
A
B
C
P
D
E
A
B
C
D
E
F
F
D
E
A
B
C
D
E
F
F
D
E
A
B
C
D
M
P
Q
O
F
A
B
C
D
M
P
Q
F
A
B
C
D
A1
B1
C1
D1
A
B
C
D
A1
B1
C1
D1
H
A
B
C
D
A1
B1
C1
D1
H
P
A
M
C
B
鳖臑
P
A
M
C
B
D
P
A
M
B
C
D
P
A
M
B
C
D
E
F
作二面角的平面角的方法
注:P点一般是题目中给出的点。
P
A
B
一作二证三计算
a
b
m
a
m
n
l
B
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
