广西钦州第四高级中学校2020-2021学年高一下学期4月第八周周测数学试题 Word版含答案
文档属性
| 名称 | 广西钦州第四高级中学校2020-2021学年高一下学期4月第八周周测数学试题 Word版含答案 | 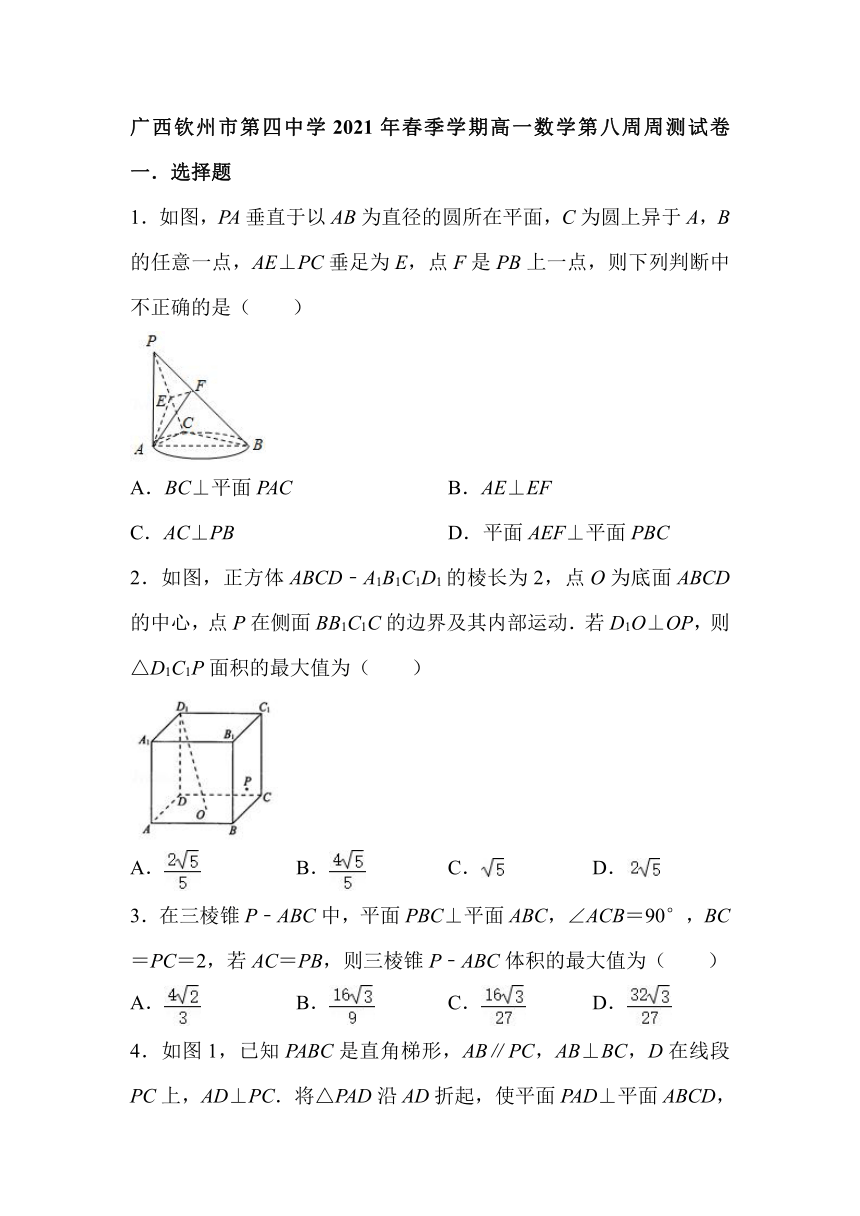 | |
| 格式 | doc | ||
| 文件大小 | 368.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-04 19:55:29 | ||
图片预览




文档简介
广西钦州市第四中学2021年春季学期高一数学第八周周测试卷一.选择题
1.如图,PA垂直于以AB为直径的圆所在平面,C为圆上异于A,B的任意一点,AE⊥PC垂足为E,点F是PB上一点,则下列判断中不正确的是( )
A.BC⊥平面PAC B.AE⊥EF
C.AC⊥PB D.平面AEF⊥平面PBC
2.如图,正方体ABCD﹣A1B1C1D1的棱长为2,点O为底面ABCD的中心,点P在侧面BB1C1C的边界及其内部运动.若D1O⊥OP,则△D1C1P面积的最大值为( )
A. B. C. D.
3.在三棱锥P﹣ABC中,平面PBC⊥平面ABC,∠ACB=90°,BC=PC=2,若AC=PB,则三棱锥P﹣ABC体积的最大值为( )
A. B. C. D.
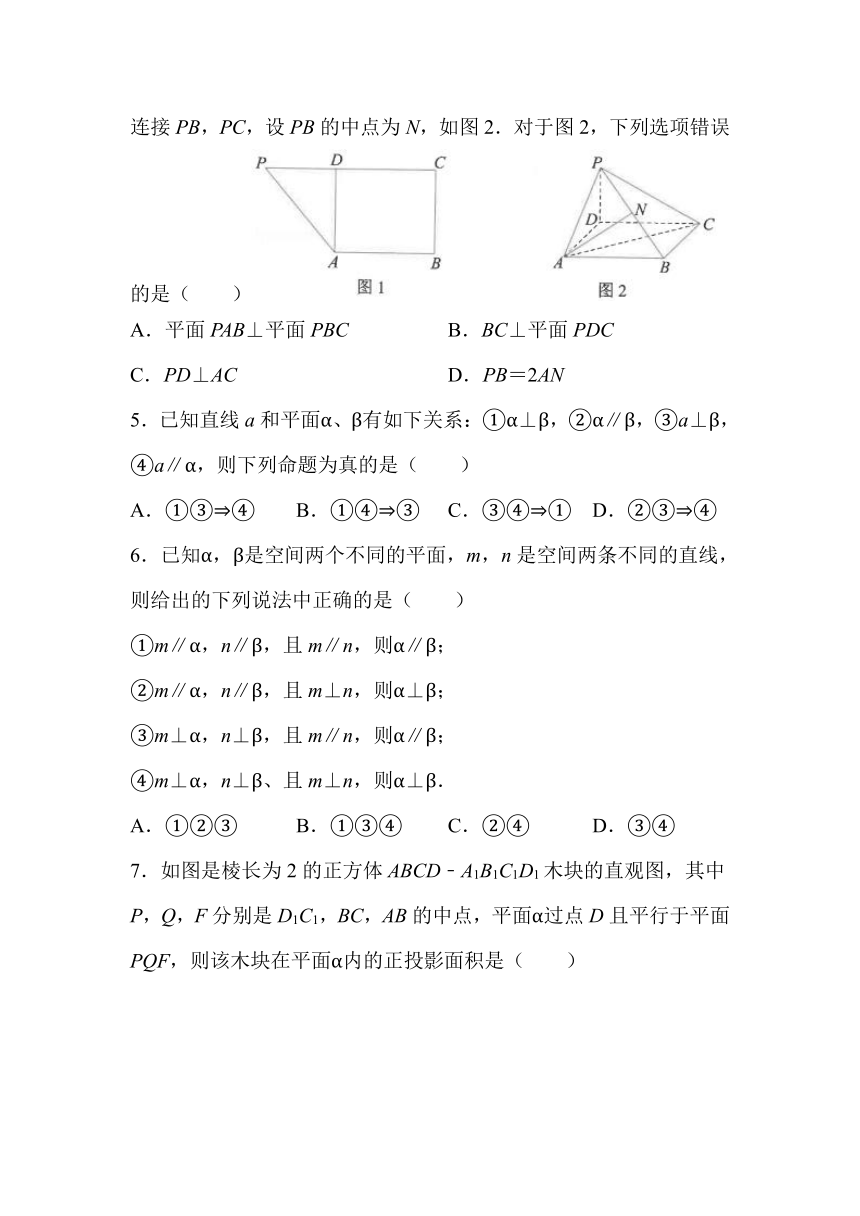
4.如图1,已知PABC是直角梯形,AB∥PC,AB⊥BC,D在线段PC上,AD⊥PC.将△PAD沿AD折起,使平面PAD⊥平面ABCD,连接PB,PC,设PB的中点为N,如图2.对于图2,下列选项错误的是( )
A.平面PAB⊥平面PBC B.BC⊥平面PDC
C.PD⊥AC D.PB=2AN
5.已知直线a和平面α、β有如下关系:①α⊥β,②α∥β,③a⊥β,④a∥α,则下列命题为真的是( )
A.①③?④ B.①④?③ C.③④?① D.②③?④
6.已知α,β是空间两个不同的平面,m,n是空间两条不同的直线,则给出的下列说法中正确的是( )
①m∥α,n∥β,且m∥n,则α∥β;
②m∥α,n∥β,且m⊥n,则α⊥β;
③m⊥α,n⊥β,且m∥n,则α∥β;
④m⊥α,n⊥β、且m⊥n,则α⊥β.
A.①②③ B.①③④ C.②④ D.③④
7.如图是棱长为2的正方体ABCD﹣A1B1C1D1木块的直观图,其中P,Q,F分别是D1C1,BC,AB的中点,平面α过点D且平行于平面PQF,则该木块在平面α内的正投影面积是( )
A. B. C. D.
8.已知四棱锥S﹣ABCD中,四边形ABCD为等腰梯形,AD∥BC,∠BAD=120°,△SAD是等边三角形,且SA=AB=2,若点P在四棱锥S﹣ABCD的外接球面上运动,记点P到平面ABCD的距离为d,若平面SAD⊥平面ABCD,则d的最大值为( )
A.+1 B.+2 C.+1 D.+2
9.已知AB是圆柱上底面的一条直径,C是上底面圆周上异于A,B的一点,D为下底面圆周上一点,且AD⊥圆柱的底面,则必有( )
A.平面ABC⊥平面BCD B.平面BCD⊥平面ACD
C.平面ABD⊥平面ACD D.平面BCD⊥平面ABD
10.如图所示,在平面多边形AQBRCSDP中,SD=PD,CR=SC,AQ=AP,点S,D,A,Q及P,D,C,R共线,四边形ABCD是正方形,沿图中虚线将它们折叠起来,使P,Q,R,S四点重合,围成一个多面体,设该几何体的互相垂直的面有n对,则( )
A.n=3 B.n=4 C.n=5 D.n=6
11.在长方体ABCD﹣A1B1C1D1中,,E为棱CD的中点,则( )
A.A1E⊥DD1 B.A1E⊥DB C.A1E⊥D1C1 D.A1E⊥DB1
12.在正四棱锥S﹣ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论,不一定成立的为( )
①EP⊥AC;②EP∥BD;③EP∥平面SBD;④EP⊥平面SAC.
A.①③ B.③④ C.①② D.②④
二.填空题
13.在正方体ABCD﹣A1B1C1D1中,M,N分别是AB,A1B1的中点,P在AD上,若平面CMN⊥平面A1BP,则= .
14.在三棱锥P﹣ABC中,AB=AC=4,∠BAC=120°,PB=PC=4,平面PBC⊥平面ABC,则三棱锥P﹣ABC外接球的表面积为 .
15.已知四边长均为2的空间四边形ABCD的顶点都在同一个球面上,若∠BAD=,平面ABD⊥平面CBD,则该球的体积为 .
16.已知平面α,β和直线m,给出条件:①m∥α;②m⊥α:③m?α;④α∥β;⑤α⊥β.当满足条件 时,m⊥β.
三.解答题
17.如图,在直三棱柱ABC﹣A1B1C1中,△ABC是正三角形,点D在棱BB1上,且BB1=3B1D,点E为B1C1的中点.
(1)证明:平面A1DE⊥平面BCC1B1;
(2)若BB1=3,AB=2,求点C到平面A1DE的距离.
18.如图,△ABC是边长为2的正三角形,△ABD是以AB为斜边的等腰直角三角形,已知CD=2.
(1)求证:平面ABC⊥平面ABD;
(2)求直线AC与平面BCD所成角的正弦值.
19.如图,在三棱柱ABC﹣A1B1C1中,D为棱BC的中点,AB⊥BC,BC⊥BB1,AB=A1B=1,BB1=.
(1)证明:A1B∥平面AC1D;
(2)证明:A1B⊥平面ABC.
20.如图1,C,D是以AB为直径的圆上两点,且AB=2AD,AC=BC,将△ABC所在的半圆沿直径AB折起,使得点C在平面ABD上的射影E在BD上,如图2.
(1)求证:BC⊥平面ACD;
(2)在线段AB上是否存在点F,使得AD∥平面CEF?若存在,求出的值;若不存在,请说明理由.
参考答案
一.选择题
1.C.2.C.3.D.4.A.5.C.6.D.7.A.8.A.9.B.10.C11.B12.D.
二.填空题
13.2.14.80π.15..16.②④.
三.解答题
17.解:(1)证明:因为三棱柱ABC﹣A1B1C1是直三棱柱,
所以BB⊥平面ABC,又A1E?平面A1B1C1,所以AE⊥BB,
因为△ABC是正三角形,所以△ABC也是正三角形,
又点E为BC的中点,所以AE⊥BC,又BB∩BC=B,
所以AE⊥平面BCCB,又AE?平面ADE,
所以平面ADE⊥平面BCCB;
(2)因为BB=3,D在棱BB上,且BB=3BD,所以BD=,
又AB=AB=2,所以在直角三角形ABD中,AD===,
同理可得DE===,
易得A1E=,所以A1D2=DE2+A1E2,
所以△A1DE为等腰直角三角形,所以△ADE的面积为S=××=,
可得S△CDE=3×2﹣×2×2﹣×1×3﹣×1×=2,
设C到平面ADE的距离为h,由(1)可知AE⊥平面CDE,
因为V=V,即S?h=S△CDE?A1E,
所以h===,
所以点C到平面ADE的距离为,
18.1)证明:取AB中点O,连OC、OD,
则OC⊥AB,OD⊥AB,
所以∠COD是二面角C﹣AB﹣D的平面角.
在△OCD中,
因为,OD=1,CD=2,
所以∠COD=90°.
所以,平面ABC⊥平面ABD.
(2)解:建立空间直角坐标系(O﹣CBD).
则,,.
设是平面BCD的法向量,
则,取.
则==,
所以直线AC与平面BCD所成角的正弦值.
19.证明:(1)连接AC交AC,与点E,连接DE,在△ABC中,D、E分别为BC、AC的中点,
所以DE∥AB,
又AB?平面ACD.DE?平面ACD.
所以AB∥平面ACD.
(2)因为AB⊥BC,BC⊥BB,AB∩BB=B,AB、BB?平面ABB.
所以BC⊥平面ABB,
又AB?平面ABB.
所以AB⊥BC;
又因为,得,
所以AB⊥AB.
又AB,BC?平面ABCAB∩BC=B,
所以AB⊥平面ABC.
20.(1)证明:∵AB是圆的直径,
∴AD⊥BD.
∵CE⊥平面ABD,AD?平面ABD,
∴CE⊥AD.
又∵CE∩BD=E,BD,CE?平面BCD,
∴AD⊥平面BCD.
∵BC?平面BCD,
∴AD⊥BC.
又∵BC⊥AC,AC∩BC=C,
∴BC⊥平面ACD.
(2)解:连接AE,∵CE⊥平面ABD,AE,BE?平面ABD,
∴CE⊥AE,CE⊥BE.
在Rt△ACE和Rt△BCE中,由AC=BC得AE=BE,
在Rt△ABD中,由AB=2AD,得∠ABD=30°,
∴∠AED=∠ABE+∠BAE=60°,
∴在Rt△ADE中,DE=AE,
∴E是BD的三等分点,且DE=EB.
在线段AB上存在点F,使得AF=FB,则有FE∥AD.
∵FE?平面CEF,AD?平面CEF,
∴AD∥平面CEF.
故在线段AB上存在点F,使得AD∥平面CEF,此时=.
1.如图,PA垂直于以AB为直径的圆所在平面,C为圆上异于A,B的任意一点,AE⊥PC垂足为E,点F是PB上一点,则下列判断中不正确的是( )
A.BC⊥平面PAC B.AE⊥EF
C.AC⊥PB D.平面AEF⊥平面PBC
2.如图,正方体ABCD﹣A1B1C1D1的棱长为2,点O为底面ABCD的中心,点P在侧面BB1C1C的边界及其内部运动.若D1O⊥OP,则△D1C1P面积的最大值为( )
A. B. C. D.
3.在三棱锥P﹣ABC中,平面PBC⊥平面ABC,∠ACB=90°,BC=PC=2,若AC=PB,则三棱锥P﹣ABC体积的最大值为( )
A. B. C. D.
4.如图1,已知PABC是直角梯形,AB∥PC,AB⊥BC,D在线段PC上,AD⊥PC.将△PAD沿AD折起,使平面PAD⊥平面ABCD,连接PB,PC,设PB的中点为N,如图2.对于图2,下列选项错误的是( )
A.平面PAB⊥平面PBC B.BC⊥平面PDC
C.PD⊥AC D.PB=2AN
5.已知直线a和平面α、β有如下关系:①α⊥β,②α∥β,③a⊥β,④a∥α,则下列命题为真的是( )
A.①③?④ B.①④?③ C.③④?① D.②③?④
6.已知α,β是空间两个不同的平面,m,n是空间两条不同的直线,则给出的下列说法中正确的是( )
①m∥α,n∥β,且m∥n,则α∥β;
②m∥α,n∥β,且m⊥n,则α⊥β;
③m⊥α,n⊥β,且m∥n,则α∥β;
④m⊥α,n⊥β、且m⊥n,则α⊥β.
A.①②③ B.①③④ C.②④ D.③④
7.如图是棱长为2的正方体ABCD﹣A1B1C1D1木块的直观图,其中P,Q,F分别是D1C1,BC,AB的中点,平面α过点D且平行于平面PQF,则该木块在平面α内的正投影面积是( )
A. B. C. D.
8.已知四棱锥S﹣ABCD中,四边形ABCD为等腰梯形,AD∥BC,∠BAD=120°,△SAD是等边三角形,且SA=AB=2,若点P在四棱锥S﹣ABCD的外接球面上运动,记点P到平面ABCD的距离为d,若平面SAD⊥平面ABCD,则d的最大值为( )
A.+1 B.+2 C.+1 D.+2
9.已知AB是圆柱上底面的一条直径,C是上底面圆周上异于A,B的一点,D为下底面圆周上一点,且AD⊥圆柱的底面,则必有( )
A.平面ABC⊥平面BCD B.平面BCD⊥平面ACD
C.平面ABD⊥平面ACD D.平面BCD⊥平面ABD
10.如图所示,在平面多边形AQBRCSDP中,SD=PD,CR=SC,AQ=AP,点S,D,A,Q及P,D,C,R共线,四边形ABCD是正方形,沿图中虚线将它们折叠起来,使P,Q,R,S四点重合,围成一个多面体,设该几何体的互相垂直的面有n对,则( )
A.n=3 B.n=4 C.n=5 D.n=6
11.在长方体ABCD﹣A1B1C1D1中,,E为棱CD的中点,则( )
A.A1E⊥DD1 B.A1E⊥DB C.A1E⊥D1C1 D.A1E⊥DB1
12.在正四棱锥S﹣ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论,不一定成立的为( )
①EP⊥AC;②EP∥BD;③EP∥平面SBD;④EP⊥平面SAC.
A.①③ B.③④ C.①② D.②④
二.填空题
13.在正方体ABCD﹣A1B1C1D1中,M,N分别是AB,A1B1的中点,P在AD上,若平面CMN⊥平面A1BP,则= .
14.在三棱锥P﹣ABC中,AB=AC=4,∠BAC=120°,PB=PC=4,平面PBC⊥平面ABC,则三棱锥P﹣ABC外接球的表面积为 .
15.已知四边长均为2的空间四边形ABCD的顶点都在同一个球面上,若∠BAD=,平面ABD⊥平面CBD,则该球的体积为 .
16.已知平面α,β和直线m,给出条件:①m∥α;②m⊥α:③m?α;④α∥β;⑤α⊥β.当满足条件 时,m⊥β.
三.解答题
17.如图,在直三棱柱ABC﹣A1B1C1中,△ABC是正三角形,点D在棱BB1上,且BB1=3B1D,点E为B1C1的中点.
(1)证明:平面A1DE⊥平面BCC1B1;
(2)若BB1=3,AB=2,求点C到平面A1DE的距离.
18.如图,△ABC是边长为2的正三角形,△ABD是以AB为斜边的等腰直角三角形,已知CD=2.
(1)求证:平面ABC⊥平面ABD;
(2)求直线AC与平面BCD所成角的正弦值.
19.如图,在三棱柱ABC﹣A1B1C1中,D为棱BC的中点,AB⊥BC,BC⊥BB1,AB=A1B=1,BB1=.
(1)证明:A1B∥平面AC1D;
(2)证明:A1B⊥平面ABC.
20.如图1,C,D是以AB为直径的圆上两点,且AB=2AD,AC=BC,将△ABC所在的半圆沿直径AB折起,使得点C在平面ABD上的射影E在BD上,如图2.
(1)求证:BC⊥平面ACD;
(2)在线段AB上是否存在点F,使得AD∥平面CEF?若存在,求出的值;若不存在,请说明理由.
参考答案
一.选择题
1.C.2.C.3.D.4.A.5.C.6.D.7.A.8.A.9.B.10.C11.B12.D.
二.填空题
13.2.14.80π.15..16.②④.
三.解答题
17.解:(1)证明:因为三棱柱ABC﹣A1B1C1是直三棱柱,
所以BB⊥平面ABC,又A1E?平面A1B1C1,所以AE⊥BB,
因为△ABC是正三角形,所以△ABC也是正三角形,
又点E为BC的中点,所以AE⊥BC,又BB∩BC=B,
所以AE⊥平面BCCB,又AE?平面ADE,
所以平面ADE⊥平面BCCB;
(2)因为BB=3,D在棱BB上,且BB=3BD,所以BD=,
又AB=AB=2,所以在直角三角形ABD中,AD===,
同理可得DE===,
易得A1E=,所以A1D2=DE2+A1E2,
所以△A1DE为等腰直角三角形,所以△ADE的面积为S=××=,
可得S△CDE=3×2﹣×2×2﹣×1×3﹣×1×=2,
设C到平面ADE的距离为h,由(1)可知AE⊥平面CDE,
因为V=V,即S?h=S△CDE?A1E,
所以h===,
所以点C到平面ADE的距离为,
18.1)证明:取AB中点O,连OC、OD,
则OC⊥AB,OD⊥AB,
所以∠COD是二面角C﹣AB﹣D的平面角.
在△OCD中,
因为,OD=1,CD=2,
所以∠COD=90°.
所以,平面ABC⊥平面ABD.
(2)解:建立空间直角坐标系(O﹣CBD).
则,,.
设是平面BCD的法向量,
则,取.
则==,
所以直线AC与平面BCD所成角的正弦值.
19.证明:(1)连接AC交AC,与点E,连接DE,在△ABC中,D、E分别为BC、AC的中点,
所以DE∥AB,
又AB?平面ACD.DE?平面ACD.
所以AB∥平面ACD.
(2)因为AB⊥BC,BC⊥BB,AB∩BB=B,AB、BB?平面ABB.
所以BC⊥平面ABB,
又AB?平面ABB.
所以AB⊥BC;
又因为,得,
所以AB⊥AB.
又AB,BC?平面ABCAB∩BC=B,
所以AB⊥平面ABC.
20.(1)证明:∵AB是圆的直径,
∴AD⊥BD.
∵CE⊥平面ABD,AD?平面ABD,
∴CE⊥AD.
又∵CE∩BD=E,BD,CE?平面BCD,
∴AD⊥平面BCD.
∵BC?平面BCD,
∴AD⊥BC.
又∵BC⊥AC,AC∩BC=C,
∴BC⊥平面ACD.
(2)解:连接AE,∵CE⊥平面ABD,AE,BE?平面ABD,
∴CE⊥AE,CE⊥BE.
在Rt△ACE和Rt△BCE中,由AC=BC得AE=BE,
在Rt△ABD中,由AB=2AD,得∠ABD=30°,
∴∠AED=∠ABE+∠BAE=60°,
∴在Rt△ADE中,DE=AE,
∴E是BD的三等分点,且DE=EB.
在线段AB上存在点F,使得AF=FB,则有FE∥AD.
∵FE?平面CEF,AD?平面CEF,
∴AD∥平面CEF.
故在线段AB上存在点F,使得AD∥平面CEF,此时=.
同课章节目录
