2020-2021学年华东师大版八年级下册18.1.1 平行四边形及其边角性质课件(第一课时 27张)
文档属性
| 名称 | 2020-2021学年华东师大版八年级下册18.1.1 平行四边形及其边角性质课件(第一课时 27张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-05 09:28:07 | ||
图片预览




文档简介
(共27张PPT)
第1课时
平行四边形及
其边角性质
第18章
平行四边形
18.1
平行四边形的性质
导入新课
观察下图,平行四边形在生活中无处不在.
情景引入
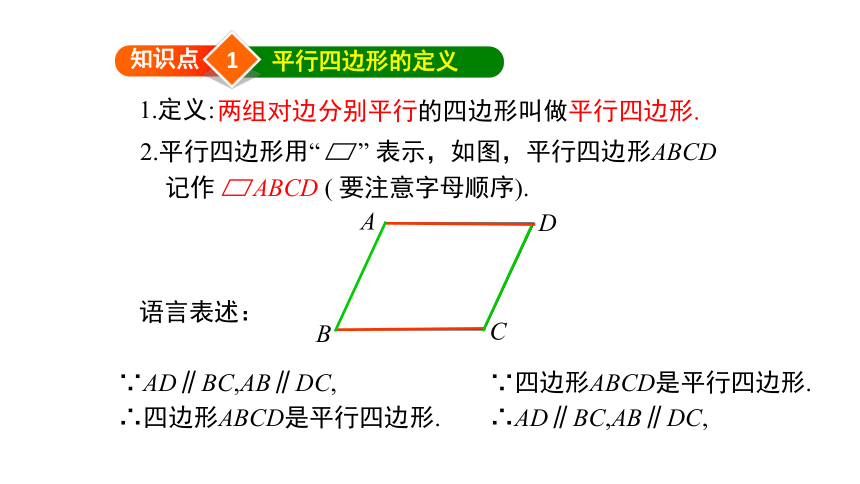
两组对边分别平行的四边形叫做平行四边形.
2.平行四边形用“
”
表示,如图,平行四边形ABCD
记作
ABCD
(
要注意字母顺序).
1.定义:
A
B
D
C
语言表述:
∵AD∥BC,AB∥DC,
∴四边形ABCD是平行四边形.
∵四边形ABCD是平行四边形.
∴AD∥BC,AB∥DC,
1
知识点
平行四边形的定义
(2)平行四边形的定义既是它的一个性质,又是它的
一种判定方法;
∵四边形ABCD是平行四边形,
反过来,
∴四边形ABCD是平行四边形.
如图,在
ABCD中,过点P作直线EF,GH分别平行于AB,BC,那么图中共有平行四边形_____个.
例1
根据平行四边形的定义,知AB∥CD,
AD∥BC,由已知可知,EF∥AB,
GH∥BC,所以根据平行四边形的定义
可以判定四边形ABFE是平行四边形,
同理可判定四边形EFCD、四边形AGHD、四边形
GBCH、四边形AGPE、四边形EPHD、四边形GBFP、
四边形PFCH都是平行四边形,最后还要加上
ABCD,
即共有9个平行四边形.
导引:
9
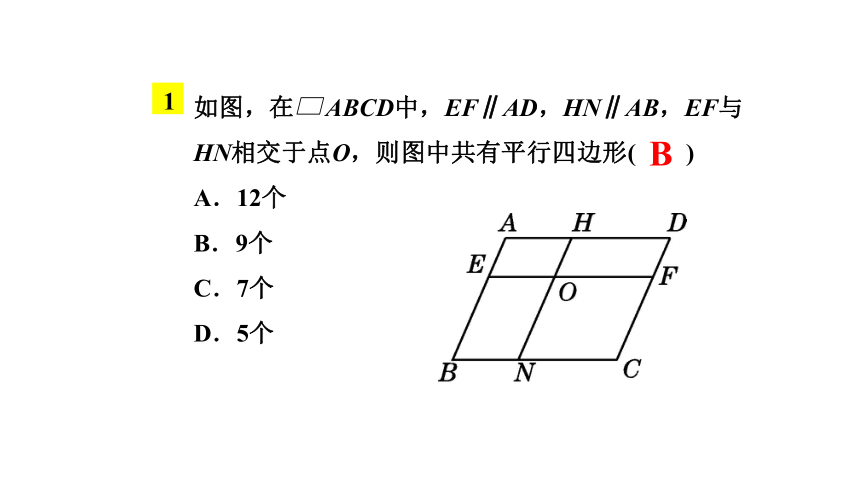
如图,在
ABCD中,EF∥AD,HN∥AB,EF与HN相交于点O,则图中共有平行四边形( )
A.12个
B.9个
C.7个
D.5个
1
B
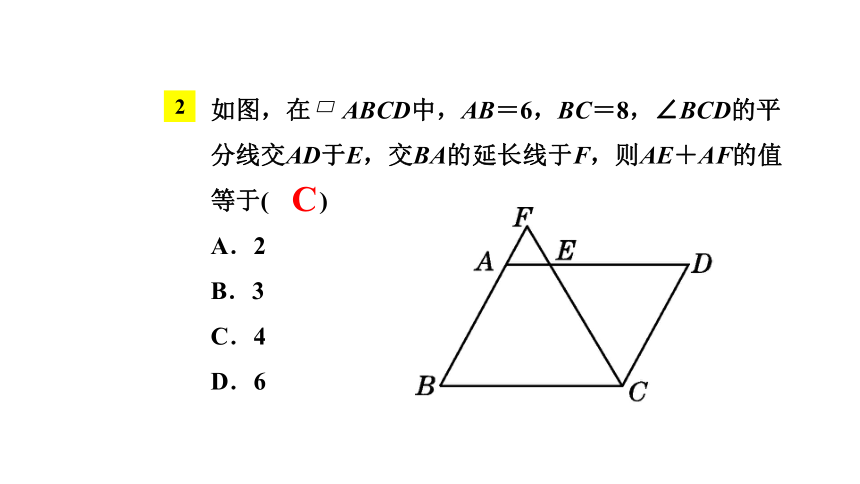
如图,在
ABCD中,AB=6,BC=8,∠BCD的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )
A.2
B.3
C.4
D.6
2
C
根据平行四边形的定义,请画一个平行四边形ABCD.
D
A
B
C
2
知识点
平行四边形的性质
A
B
C
D
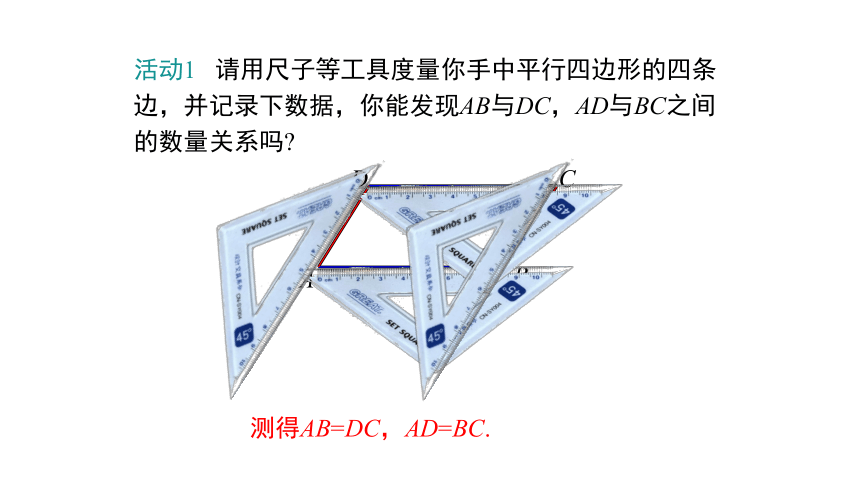
活动1
请用尺子等工具度量你手中平行四边形的四条边,并记录下数据,你能发现AB与DC,AD与BC之间的数量关系吗?
测得AB=DC,AD=BC.
A
B
C
D
测得∠A
=∠C,∠B
=∠D.
活动2
请用量角器等工具度量你手中平行四边形的四个角,并记录下数据,你能发现∠A与∠C,∠B与
∠D之间的数量关系吗?
猜想
平行四边形的两组对边,两组对角有什么数量关系?
两组对边及两组对角分别相等.且邻角互补
怎样证明这个猜想呢?
证明:如图,连接AC.
∵四边形ABCD是平行四边形,
∴AD∥BC,AB
∥
CD,
∴∠1=∠2,∠3=∠4.
又∵AC是△ABC和△CDA的公共边,
∴
△ABC≌△CDA,
∴AD=BC,AB=CD,∠ABC=∠ADC.
∵∠BAD=∠1+∠4,∠BCD=∠2+∠3,
∴∠BAD=∠BCD.
A
B
C
D
1
4
3
2
已知:四边形ABCD是平行四边形.
求证:AD=BC,AB=CD,∠BAD=∠BCD,∠ABC=∠ADC.
证一证
思考
不添加辅助线,你能否直接运用平行四边形的
定义,证明其对角相等?
A
B
C
D
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB
∥
CD,
∴∠A+∠B=180°,
∠A+∠D=180°,
∴∠B=∠D.
同理可得∠A=∠C.
几
何
语
言
边
角
文字叙述
对边平行
对边相等
对角相等
(邻角互补)
∵
四边形ABCD是平行四边形,
∴
AD∥BC
,AB∥DC.
∴
AD=BC
,AB=DC.
∵
四边形ABCD是平行四边形,
∴
∠
A=∠C,∠
B=∠D.
∵
四边形ABCD是平行四边形,
A
B
C
D
平行四边形的性质
知识要点
性质定理1
性质定理2
如图,
在
ABCD中,AB=
8,
周长等于24.
求其
余三条边的长.
例2
在
ABCD中,
AB
=
DC,AD
=
BC(平行四边形的对边相等).
∵AB=8,
∴
DC=8
,
又∵AB+BC+DC+AD=24,
∴AD=BC
=
(24-2AB)=4.
解:
A
B
C
D
已知平行四边形的周长是24,
相邻两边的长度相
差4,求该平行四边形相邻两边的长.
例3
如图,
设AB的长为x,
则BC的长为x+4.
根据已知,可得
2(AB+BC)=24,
即
2(x+x+4)=24,
4x+8=24,
解得
x=4.
所以,该平行四边形相邻两边的长分别为4和8.
解:
在平行四边形中,两邻边长之和等于周长的一半.
已知:如图,
在
ABCD
中,∠ADC的平分线与
AB相交于点E.
求证:BE+
BC
=
CD.
例4
四边形ABCD是平行四边形,
∴AB=CD(平行四边形的对边相等),
AB//CD(平行四边形的对边平行),
∴∠CDE
=∠AED.
又∵DE是∠ADC的平分线,
∴∠ADE
=∠CDE,
∴∠ADE
=∠AED,
∴AD
=
AE.
又∵AD=BC
(平行四边形的对边相等)
∴AE=BC.
∴BE+BC=BE+AE=AB=CD.
证明:
平行四边形一内角的平分线与对边相交于一点,可得到一个等腰三角形.
如图,
在
ABCD中,∠A
=40°,求其他各内角
的大小.
例5
在
ABCD中,
∠A
=
∠C,∠B
=
∠D(平行四边形的对角相等).
∵∠A=40°,∴∠C=40°.
又∵AD//BC,
∴∠A
+
∠B
=
180°,
∴∠B
=
180°
-
∠A=180°-
40°
=
140°,
∴∠D
=
∠B
=
140°.
解:
如图,在
ABCD中,已知∠A+∠C=120°,求平行四边形各角的度数.
例6
在
ABCD中,∠A=∠C,∠B=∠D.
∵∠A+∠C=120°,∴∠A=∠C=60°.
∴∠D=180°-∠A=180°-60°=120°.
∴∠B=∠D=120°.
解:
例4
如图,在
ABCD中,DE⊥AB,BF⊥CD,垂足分别是E,F.求证:AE=CF.
证明:
∵四边形ABCD是平行四边形,
∴
∠A=
∠C,AD=CB.
又∠AED=
∠CFB=90°,
∴
△ADE≌△CBF(A.A.S.),
∴AE=CF.
思考
在上述证明中还能得出什么结论?
D
A
B
C
F
E
DE=BF
3
知识点
平行线之间的距离
C
B
F
E
A
D
若m
//
n,作
AB
//
CD
//
EF,分别交
m于A、C、E,交
n于B、D、F.
由平行四边形的性质得AB=CD=EF.
夹在两条平行线间的平行线段相等.
m
n
由平行四边形的定义易知四边形ABDC,CDFE均为平行四边形.
归纳总结
平行线间的距离处处相等.
若m
//
n,AB、CD、EF垂直于
n,交n于B、D、F,交
m于A、C、E.
B
F
E
A
n
m
C
D
点到直线的距离
同前面易得AB=CD=EF
两条平行线间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离
要点精析:
(1)“平行线间的距离处处相等”,在作平行四边形的
高时,可根据需要灵活选择位置;(注:平行线的
这一性质常用来解决三角形同底等高问题)
(2)平行线的位置确定后,它们间的距离是定值(是正
值),不随垂线段位置的改变而改变.
数学表达式:
如图,A,C是l1上任意两点,
∵l1∥l2,AB⊥l2,CD⊥l2,
∴AB=CD.
拓展:
(1)夹在两条平行线间的任何平行线段都相等;
(2)等底等高的三角形的面积相等.
例7
如图,直线a∥b,点A,E,F在直线a上,点B,C,D在直线b上,BC=EF.
△ABC与△DEF的
面积相等吗?为什么?
解:
△ABC和△DEF的面积相等.理由如下:
如图,作AH1⊥直线b,垂足为点H1,
作DH2⊥直线a,垂足为点H2.
设△ABC和△DEF的面积分别为S1和S2,
∴S1=
BC·AH1,
S2=
EF·DH2.
∵直线a∥b,AH1⊥直线b,
DH2⊥直线a,
∴AH1=DH2.
又∵BC=EF,∴S1=S2,
即△ABC与△DEF的面积相等.
如图,a∥b,AB∥CD,CE⊥b,FG⊥b,E,G为垂足,则下列说法不正确的是( )
A.AB=CD
B.EC=FG
C.A,B两点间的距离就是线段AB的长度
D.a与b的距离就是线段CD的长度
2
D
平行
四边形
定义
两组对边分别平行的四边形
性质
两组对边分别平行且相等
平行线间的距离处处相等
两组对角分别相等,邻角互补
第1课时
平行四边形及
其边角性质
第18章
平行四边形
18.1
平行四边形的性质
导入新课
观察下图,平行四边形在生活中无处不在.
情景引入
两组对边分别平行的四边形叫做平行四边形.
2.平行四边形用“
”
表示,如图,平行四边形ABCD
记作
ABCD
(
要注意字母顺序).
1.定义:
A
B
D
C
语言表述:
∵AD∥BC,AB∥DC,
∴四边形ABCD是平行四边形.
∵四边形ABCD是平行四边形.
∴AD∥BC,AB∥DC,
1
知识点
平行四边形的定义
(2)平行四边形的定义既是它的一个性质,又是它的
一种判定方法;
∵四边形ABCD是平行四边形,
反过来,
∴四边形ABCD是平行四边形.
如图,在
ABCD中,过点P作直线EF,GH分别平行于AB,BC,那么图中共有平行四边形_____个.
例1
根据平行四边形的定义,知AB∥CD,
AD∥BC,由已知可知,EF∥AB,
GH∥BC,所以根据平行四边形的定义
可以判定四边形ABFE是平行四边形,
同理可判定四边形EFCD、四边形AGHD、四边形
GBCH、四边形AGPE、四边形EPHD、四边形GBFP、
四边形PFCH都是平行四边形,最后还要加上
ABCD,
即共有9个平行四边形.
导引:
9
如图,在
ABCD中,EF∥AD,HN∥AB,EF与HN相交于点O,则图中共有平行四边形( )
A.12个
B.9个
C.7个
D.5个
1
B
如图,在
ABCD中,AB=6,BC=8,∠BCD的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )
A.2
B.3
C.4
D.6
2
C
根据平行四边形的定义,请画一个平行四边形ABCD.
D
A
B
C
2
知识点
平行四边形的性质
A
B
C
D
活动1
请用尺子等工具度量你手中平行四边形的四条边,并记录下数据,你能发现AB与DC,AD与BC之间的数量关系吗?
测得AB=DC,AD=BC.
A
B
C
D
测得∠A
=∠C,∠B
=∠D.
活动2
请用量角器等工具度量你手中平行四边形的四个角,并记录下数据,你能发现∠A与∠C,∠B与
∠D之间的数量关系吗?
猜想
平行四边形的两组对边,两组对角有什么数量关系?
两组对边及两组对角分别相等.且邻角互补
怎样证明这个猜想呢?
证明:如图,连接AC.
∵四边形ABCD是平行四边形,
∴AD∥BC,AB
∥
CD,
∴∠1=∠2,∠3=∠4.
又∵AC是△ABC和△CDA的公共边,
∴
△ABC≌△CDA,
∴AD=BC,AB=CD,∠ABC=∠ADC.
∵∠BAD=∠1+∠4,∠BCD=∠2+∠3,
∴∠BAD=∠BCD.
A
B
C
D
1
4
3
2
已知:四边形ABCD是平行四边形.
求证:AD=BC,AB=CD,∠BAD=∠BCD,∠ABC=∠ADC.
证一证
思考
不添加辅助线,你能否直接运用平行四边形的
定义,证明其对角相等?
A
B
C
D
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB
∥
CD,
∴∠A+∠B=180°,
∠A+∠D=180°,
∴∠B=∠D.
同理可得∠A=∠C.
几
何
语
言
边
角
文字叙述
对边平行
对边相等
对角相等
(邻角互补)
∵
四边形ABCD是平行四边形,
∴
AD∥BC
,AB∥DC.
∴
AD=BC
,AB=DC.
∵
四边形ABCD是平行四边形,
∴
∠
A=∠C,∠
B=∠D.
∵
四边形ABCD是平行四边形,
A
B
C
D
平行四边形的性质
知识要点
性质定理1
性质定理2
如图,
在
ABCD中,AB=
8,
周长等于24.
求其
余三条边的长.
例2
在
ABCD中,
AB
=
DC,AD
=
BC(平行四边形的对边相等).
∵AB=8,
∴
DC=8
,
又∵AB+BC+DC+AD=24,
∴AD=BC
=
(24-2AB)=4.
解:
A
B
C
D
已知平行四边形的周长是24,
相邻两边的长度相
差4,求该平行四边形相邻两边的长.
例3
如图,
设AB的长为x,
则BC的长为x+4.
根据已知,可得
2(AB+BC)=24,
即
2(x+x+4)=24,
4x+8=24,
解得
x=4.
所以,该平行四边形相邻两边的长分别为4和8.
解:
在平行四边形中,两邻边长之和等于周长的一半.
已知:如图,
在
ABCD
中,∠ADC的平分线与
AB相交于点E.
求证:BE+
BC
=
CD.
例4
四边形ABCD是平行四边形,
∴AB=CD(平行四边形的对边相等),
AB//CD(平行四边形的对边平行),
∴∠CDE
=∠AED.
又∵DE是∠ADC的平分线,
∴∠ADE
=∠CDE,
∴∠ADE
=∠AED,
∴AD
=
AE.
又∵AD=BC
(平行四边形的对边相等)
∴AE=BC.
∴BE+BC=BE+AE=AB=CD.
证明:
平行四边形一内角的平分线与对边相交于一点,可得到一个等腰三角形.
如图,
在
ABCD中,∠A
=40°,求其他各内角
的大小.
例5
在
ABCD中,
∠A
=
∠C,∠B
=
∠D(平行四边形的对角相等).
∵∠A=40°,∴∠C=40°.
又∵AD//BC,
∴∠A
+
∠B
=
180°,
∴∠B
=
180°
-
∠A=180°-
40°
=
140°,
∴∠D
=
∠B
=
140°.
解:
如图,在
ABCD中,已知∠A+∠C=120°,求平行四边形各角的度数.
例6
在
ABCD中,∠A=∠C,∠B=∠D.
∵∠A+∠C=120°,∴∠A=∠C=60°.
∴∠D=180°-∠A=180°-60°=120°.
∴∠B=∠D=120°.
解:
例4
如图,在
ABCD中,DE⊥AB,BF⊥CD,垂足分别是E,F.求证:AE=CF.
证明:
∵四边形ABCD是平行四边形,
∴
∠A=
∠C,AD=CB.
又∠AED=
∠CFB=90°,
∴
△ADE≌△CBF(A.A.S.),
∴AE=CF.
思考
在上述证明中还能得出什么结论?
D
A
B
C
F
E
DE=BF
3
知识点
平行线之间的距离
C
B
F
E
A
D
若m
//
n,作
AB
//
CD
//
EF,分别交
m于A、C、E,交
n于B、D、F.
由平行四边形的性质得AB=CD=EF.
夹在两条平行线间的平行线段相等.
m
n
由平行四边形的定义易知四边形ABDC,CDFE均为平行四边形.
归纳总结
平行线间的距离处处相等.
若m
//
n,AB、CD、EF垂直于
n,交n于B、D、F,交
m于A、C、E.
B
F
E
A
n
m
C
D
点到直线的距离
同前面易得AB=CD=EF
两条平行线间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离
要点精析:
(1)“平行线间的距离处处相等”,在作平行四边形的
高时,可根据需要灵活选择位置;(注:平行线的
这一性质常用来解决三角形同底等高问题)
(2)平行线的位置确定后,它们间的距离是定值(是正
值),不随垂线段位置的改变而改变.
数学表达式:
如图,A,C是l1上任意两点,
∵l1∥l2,AB⊥l2,CD⊥l2,
∴AB=CD.
拓展:
(1)夹在两条平行线间的任何平行线段都相等;
(2)等底等高的三角形的面积相等.
例7
如图,直线a∥b,点A,E,F在直线a上,点B,C,D在直线b上,BC=EF.
△ABC与△DEF的
面积相等吗?为什么?
解:
△ABC和△DEF的面积相等.理由如下:
如图,作AH1⊥直线b,垂足为点H1,
作DH2⊥直线a,垂足为点H2.
设△ABC和△DEF的面积分别为S1和S2,
∴S1=
BC·AH1,
S2=
EF·DH2.
∵直线a∥b,AH1⊥直线b,
DH2⊥直线a,
∴AH1=DH2.
又∵BC=EF,∴S1=S2,
即△ABC与△DEF的面积相等.
如图,a∥b,AB∥CD,CE⊥b,FG⊥b,E,G为垂足,则下列说法不正确的是( )
A.AB=CD
B.EC=FG
C.A,B两点间的距离就是线段AB的长度
D.a与b的距离就是线段CD的长度
2
D
平行
四边形
定义
两组对边分别平行的四边形
性质
两组对边分别平行且相等
平行线间的距离处处相等
两组对角分别相等,邻角互补
