等差数列求和
图片预览





文档简介
(共16张PPT)
等差数列定义:
公 差 :
通项公式:
等差中项:
重要性质:
(1)当m+n=p+q时, am+an=ap+aq
注意:这里m,n,p,q N*
an+1-an=d(常数)
d
an=a1+(n-1)d
(2)(a1+an)=(a2+an-1)=(a3+an-2)=…
研究的问题:
探索已知等差数列的首项
为a1,项数为n ,第n项an,求它的
前n项和
的计算公式.
Sn= a1+ a2 + a3 + … +an-2+an-1+an
等差数列前n项和公式推导:
2Sn=(a1+an)+(a1+an)+ … +(a1+an)
多少个(a1+an)
共有 n 个(a1+an)
把 + 得:2Sn=(a1+an)+(a2+an-1)+(a3+an-2)+…+(an+a1)
由等差数列的性质知:
a1+an=a2+an-1=a3+an-2=…=an+a1,所以 式可化为:
= n(a1+an)
这种求和的方法叫倒序相加!
因此,
Sn= a1+ a2 + a3 + … +an-2+an-1+an
(公式1)
(公式2)
尝试:
Sn= an+ an-1 + an-2 + … +a3+a2+a1
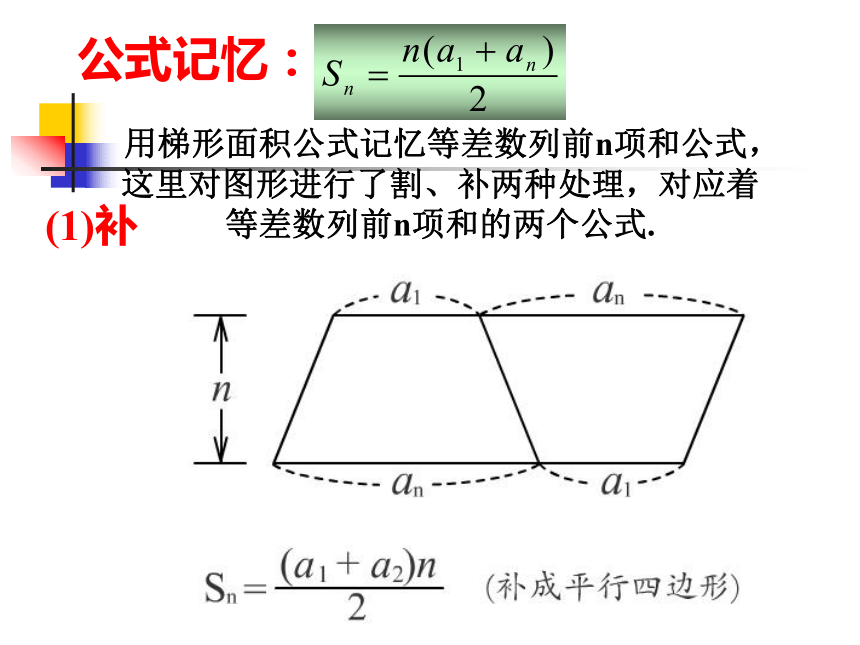
公式记忆:
用梯形面积公式记忆等差数列前n项和公式,
这里对图形进行了割、补两种处理,对应着
等差数列前n项和的两个公式.
(1)补
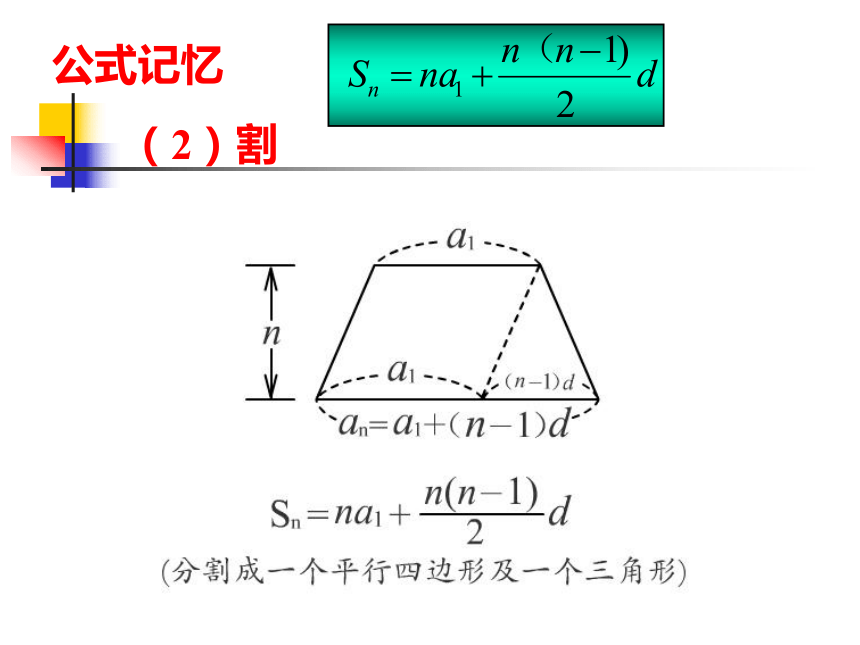
公式记忆
(2)割
分析:此应用题可以归结为什么数学问题,如何给出其中的量?
关键:分析题意建立数学模型
解:由题意可知,这个V形架上共放着120层铅笔,
且自下而上各层的铅笔数组成等差数列,记为
例1 一个堆放铅笔的V形架的最下面一层放1支铅笔,往上每一层都比它下面一层多放一支,最上面一层放120支. 这个V形架上共放着多少支铅笔?
答:这个V形架上共放着7260支铅笔.
例2:
等差数列-10,-6,-2,2,···前多少项的和是54?
解: 设题中的等差数列为{an},前n项和是Sn,则a1=-10,d=-6-(-10)=4令Sn=54,根据等差数列前项和公式,得:
-10n +
n(n-1)
2
×4
=54
解得: n1=9, n2=-3
n -6n-27=0
2
整理得:
答: 等差数列-10,-6,-2,2,···前9项的和是54。
(舍去)
巩固练习:
1) 等差数列5, 4, 3, 2 …前多少项的和是-30
a1=5
d=-1
sn=-30
即
n a1 +
n(n-1)d
2
=-30
n=15
简解:
2) 根据下列各题中的条件,求相应的等差数列{an}的有关未知数:
(1)a1=2, an=24, Sn=156, 求d及n;
巩固练习:
∴n=12
∴ d=2
629=37
简解
(2) d= , n =37, Sn=629,求a1及an;
(1)数列{an}是以 为首项,以d为公差的等差数列,如果a1+a2+a3=12,a8+a9+a10=75,求d , , 。
由a1+a2+a3=12,
a8+a9+a10=75,
解得a1=1,d=3
∴ 3a1+3d=12
∴ 3a1+24d=75
解:
①
②
∴
由①与②
=
+
d
10
=
1+
3
=
145
10
解法2:
由a1+a2+a3=12,
∴
=
4
a8+a9+a10=75,
∴
=
25
=
+
7d
由
∴
d=3,
a1=1
=
=
=145
巩固提高
思考题:
在等差数列{an}中
①已知a2+a5+a12+a15=36 求S16
②已知a6=400 求S11
解:
①
②
整体思想解决数学问题
已知一个等差数列的前10项的和是310,前20项的和是1220,由此可以确定求其前n项和的公式吗?
解:由题设:
得:
∴
巩固提高
片头
等差数列定义:
公 差 :
通项公式:
等差中项:
重要性质:
(1)当m+n=p+q时, am+an=ap+aq
注意:这里m,n,p,q N*
an+1-an=d(常数)
d
an=a1+(n-1)d
(2)(a1+an)=(a2+an-1)=(a3+an-2)=…
研究的问题:
探索已知等差数列的首项
为a1,项数为n ,第n项an,求它的
前n项和
的计算公式.
Sn= a1+ a2 + a3 + … +an-2+an-1+an
等差数列前n项和公式推导:
2Sn=(a1+an)+(a1+an)+ … +(a1+an)
多少个(a1+an)
共有 n 个(a1+an)
把 + 得:2Sn=(a1+an)+(a2+an-1)+(a3+an-2)+…+(an+a1)
由等差数列的性质知:
a1+an=a2+an-1=a3+an-2=…=an+a1,所以 式可化为:
= n(a1+an)
这种求和的方法叫倒序相加!
因此,
Sn= a1+ a2 + a3 + … +an-2+an-1+an
(公式1)
(公式2)
尝试:
Sn= an+ an-1 + an-2 + … +a3+a2+a1
公式记忆:
用梯形面积公式记忆等差数列前n项和公式,
这里对图形进行了割、补两种处理,对应着
等差数列前n项和的两个公式.
(1)补
公式记忆
(2)割
分析:此应用题可以归结为什么数学问题,如何给出其中的量?
关键:分析题意建立数学模型
解:由题意可知,这个V形架上共放着120层铅笔,
且自下而上各层的铅笔数组成等差数列,记为
例1 一个堆放铅笔的V形架的最下面一层放1支铅笔,往上每一层都比它下面一层多放一支,最上面一层放120支. 这个V形架上共放着多少支铅笔?
答:这个V形架上共放着7260支铅笔.
例2:
等差数列-10,-6,-2,2,···前多少项的和是54?
解: 设题中的等差数列为{an},前n项和是Sn,则a1=-10,d=-6-(-10)=4令Sn=54,根据等差数列前项和公式,得:
-10n +
n(n-1)
2
×4
=54
解得: n1=9, n2=-3
n -6n-27=0
2
整理得:
答: 等差数列-10,-6,-2,2,···前9项的和是54。
(舍去)
巩固练习:
1) 等差数列5, 4, 3, 2 …前多少项的和是-30
a1=5
d=-1
sn=-30
即
n a1 +
n(n-1)d
2
=-30
n=15
简解:
2) 根据下列各题中的条件,求相应的等差数列{an}的有关未知数:
(1)a1=2, an=24, Sn=156, 求d及n;
巩固练习:
∴n=12
∴ d=2
629=37
简解
(2) d= , n =37, Sn=629,求a1及an;
(1)数列{an}是以 为首项,以d为公差的等差数列,如果a1+a2+a3=12,a8+a9+a10=75,求d , , 。
由a1+a2+a3=12,
a8+a9+a10=75,
解得a1=1,d=3
∴ 3a1+3d=12
∴ 3a1+24d=75
解:
①
②
∴
由①与②
=
+
d
10
=
1+
3
=
145
10
解法2:
由a1+a2+a3=12,
∴
=
4
a8+a9+a10=75,
∴
=
25
=
+
7d
由
∴
d=3,
a1=1
=
=
=145
巩固提高
思考题:
在等差数列{an}中
①已知a2+a5+a12+a15=36 求S16
②已知a6=400 求S11
解:
①
②
整体思想解决数学问题
已知一个等差数列的前10项的和是310,前20项的和是1220,由此可以确定求其前n项和的公式吗?
解:由题设:
得:
∴
巩固提高
片头
