鲁教版(五四制)八年级下册数学 第六章 回顾与思考 课件(31张)
文档属性
| 名称 | 鲁教版(五四制)八年级下册数学 第六章 回顾与思考 课件(31张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-05 09:47:40 | ||
图片预览







文档简介
思维自疑问和惊奇开始
——亚里士多德
特殊平行四边形复习课
学习目标
1、进一步理解几种特殊平行四边形的概
念、性质及其相互间的区别和联系。
2、灵活运用特殊平行四边形的性质解决
实际问题。
3、体会类比思想、数形结合思想在数学
中的应用,提升学生分析问题、解决问
题的能力,培养学生的发散思维。
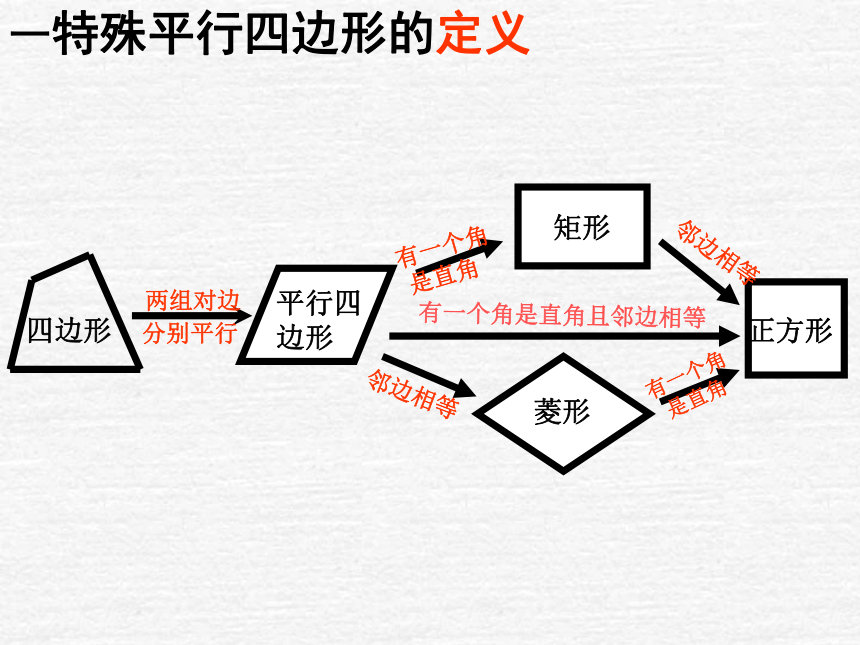
一特殊平行四边形的定义
四边形
平行四边形
矩形
菱形
正方形
有一个角
是直角
邻边相等
邻边相等
有一个角
是直角
有一个角是直角且邻边相等
两组对边
分别平行
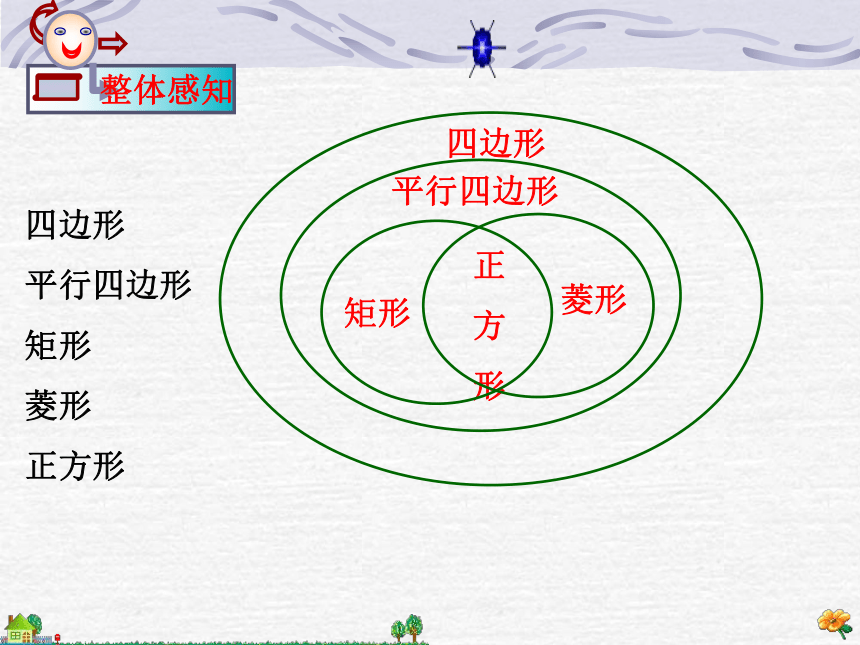
四边形
平行四边形
矩形
菱形
正方形
平行四边形
矩形
四边形
菱形
正
方
形
整体感知
A
B
C
D
B
A
C
D
A
B
C
D
性质探究一:(边上具备哪些性质?)
C
B
D
A
性质 探究 一
平行四边形:对边平行且相等
矩形: 对边平行且相等
菱形: 对边平行,四条边都相等
正方形:对边平行,四条边都相等
注意区别哟!
A
B
C
D
B
A
C
D
A
B
C
D
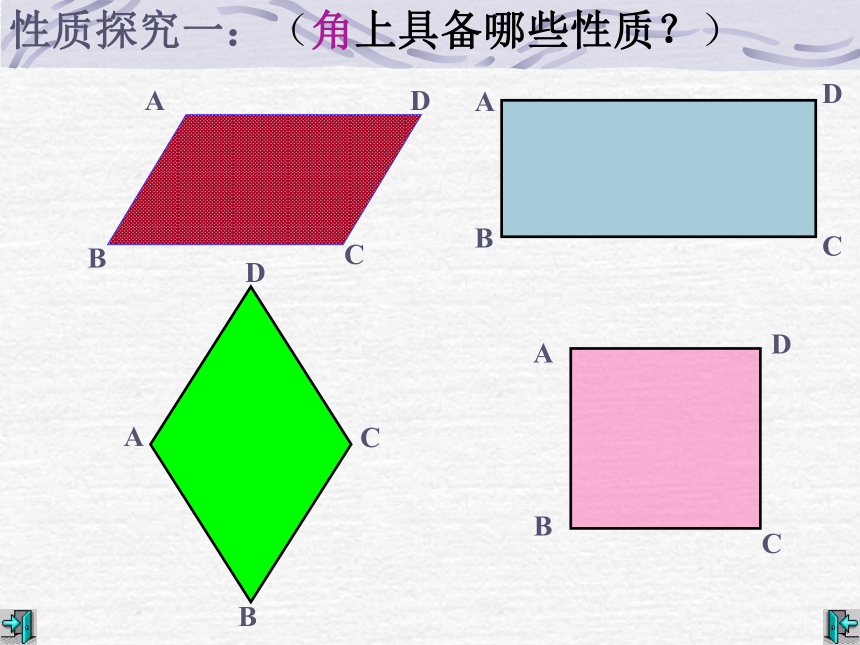
性质探究一:(角上具备哪些性质?)
C
B
D
A
平行四边形:对角相等
矩形:四个角都是直角
菱形:对角相等
正方形:四个角都是直角
性质 探究 二
A
B
C
D
O
B
O
A
C
D
A
B
C
D
O
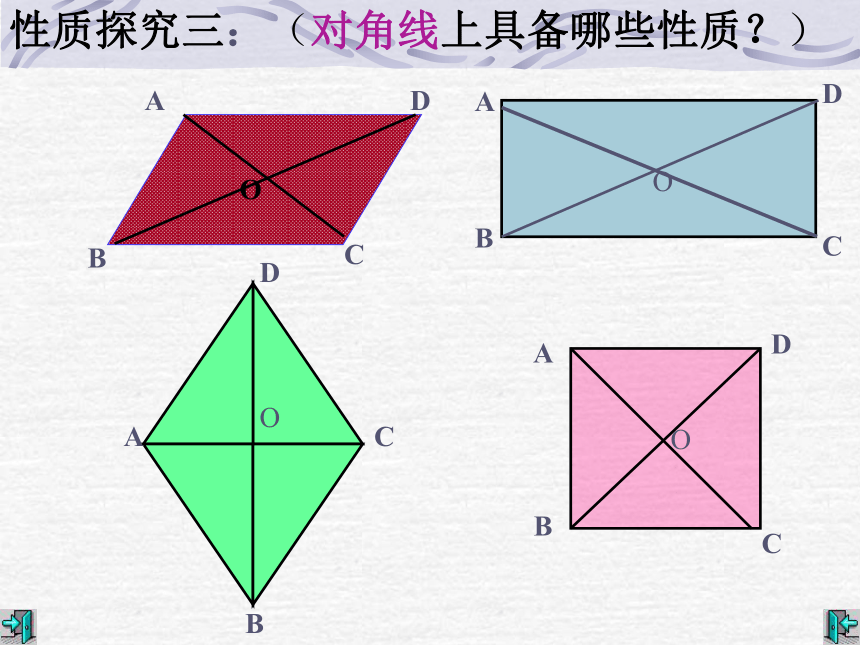
性质探究三:(对角线上具备哪些性质?)
C
B
D
O
A
平行四边形:对角线互相平分
矩形:对角线互相平分且相等
菱形:对角线互相垂直平分,并且每条对角线平分一组对角
正方形:对角线互相垂直平分且相等,每条对 角线平分一组对角
性质 探究 三
A
B
C
D
O
B
O
A
C
D
A
B
C
D
O
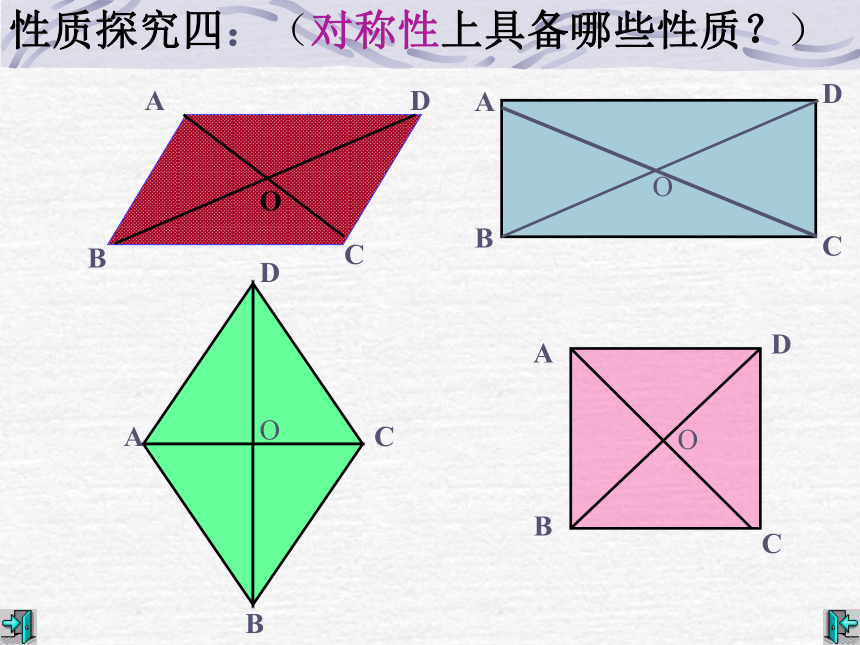
性质探究四:(对称性上具备哪些性质?)
C
B
D
O
A
平行四边形:中心对称图形
矩形:中心对称图形、轴对称图形
菱形:中心对称图形、轴对称图形
正方形:中心对称图形、轴对称图形
性质 探究 四
二、几种特殊平行四边形的性质
平行
四边形
矩 形
菱 形
正方形
边
对边平行
且相等
对边平行
且相等
对边平行,四条边都相等
对边平行,
四条边
都相等
角
对角相等
四个角
都是直角
对角相等
四个角
都是直角
对 角 线
两条对角线互相平分
两条对角线互相平分且相等
两条对角线互相垂直平分,
每条对角线平分一组对角
两条对角线互相垂直平分
且相等,每条对角线平分
一组对角
对称性
中心对称
轴对称
中心对称
轴对称
中心对称
轴对称
中心对称
A
B
C
D
O
B
O
A
C
D
A
B
C
D
O
三:探索特殊平行四边形被两条对角线分成的几个三角形间的关系
C
B
D
O
A
正方形
正方形
学以致用
挑战自我
勇攀高峰
积极抢答
相信自己是最棒的!
(一)判断题:
1.平行四边形的对角线相等 ( )
2.矩形的四个角都相等 ( )
3.菱形的对角线互相垂直平分 且相等( )
4. 正方形既是平行四边形,又是矩形,又是菱形,所以它具备它们所具有的所有性质( )
5.正方形既是轴对称图形又是中心对称图形
( )
1
夯实基础,针对训练
3.如图,菱形ABCD的周长是52cm,一条对角线长是24cm,则它的面积是 _______cm.
1.如图,□ ABCD的对角线AC、BD长度之和为20cm,若△OAD的周长为17cm,则AD=____cm
2
2.矩形的一内角平分线把矩形的一条边分成3和5两部分,则该矩形的周长_________
A
B
C
D
O
7
(二)填空题:
22或26
O
A
D
C
B
120
4.如图,在菱形ABCD中,∠BAD= 60°,周长为16cm,则较短的对角线长为( )
A
A 4 √3cm B 2√3 cm
C 2 cm
D 4 cm
B
C
D
O
D
知识反馈,形成能力
2
O
讨论:用两个全等的不等边三角形纸片可以拼出几种形状不同的平行四边形?
(小结:平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。)
小组探究
6
动手画一画!
6 如图,EF过矩形ABCD对角线的交点O,且分别交于AB、CD于E、F,那么图中阴影部分的面积是矩形ABCD
A:1/5 B:1/4 C:1/3 D:3/10
的面积的( )
D
F
B
活学活用,形成技巧
3
A
B
C
O
E
如图,正方形ABCD的两条对角线相交于点O,O又是正方形EFMO的一个顶点,两个正方形的边长都为2,那么两个正方形重叠部分的面积为多少?
A
B
E
C
D
O
F
M
挑战自我!
M
N
答案:1
4 自我拓展,励志成功
A
B
E
C
D
O
F
M
答案:1
变式1:如果正方形EFMO的边长变为4,那么图中重叠部分的面积又为多少?
变式2:边长变为a呢?
A
B
E
C
D
O
F
M
思考:通过这道题,你能得出什么结论?
变式三:正方形EFMO变为任意多边形,但是满足∠EON=90度,重叠部分的面积有没有变化?
结论:无论多边形如何改变,只要∠EON=90度,重叠部分的面积就始终等于正方形ABCD面积的1/4
N
答案:1
将五个边长都是2的正方形如图摆放,点A、B、C、D、E分别是正方形的中心,则图中阴影部分的面积是__。
4
已知:如图所示,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,过A作AG⊥EB,垂足为G,AG交BD于F
求证:OE=OF
O
G
F
A
B
C
D
E
5 自我拓展,励志成功
如图,折叠矩形的一边AD,点D落在BC边上点F处,已知AB=8,BC=10,则EC的长是多少?
B
C
A
D
E
F
解:设EC=x,则DE=8-x,
由轴对称可知: EF=DE=8-x,AF=AD=10,又因AB=8,
故BF=6,故FC=BC-BF=4。
在Rt?FCE中,
42+x =(8-x) ,
解得 x=3
2
2
A
P
E
D
C
B
.
.
5.如图:菱形ABCD中AB=2,∠B=120°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是_________ .
3
√
□ABCD的周长为32cm, ∠ABC的角平分线交边AD所在直线于点E,且AE:ED
=3:2,则AB=______________.
6cm或12cm
链接中考
A
B
C
D
E
A
B
C
D
E
3x
3x
2x
x
2x
3x
如图,已知,在正方形ABCD中,E、F分别是BC,CD上的点,且∠EAF=45度.
求证:EF=BE+FD
下课了!
结束寄语
学如三角形
一角信心
一角方法
一角勤奋
三角合定,学有稳定
——亚里士多德
特殊平行四边形复习课
学习目标
1、进一步理解几种特殊平行四边形的概
念、性质及其相互间的区别和联系。
2、灵活运用特殊平行四边形的性质解决
实际问题。
3、体会类比思想、数形结合思想在数学
中的应用,提升学生分析问题、解决问
题的能力,培养学生的发散思维。
一特殊平行四边形的定义
四边形
平行四边形
矩形
菱形
正方形
有一个角
是直角
邻边相等
邻边相等
有一个角
是直角
有一个角是直角且邻边相等
两组对边
分别平行
四边形
平行四边形
矩形
菱形
正方形
平行四边形
矩形
四边形
菱形
正
方
形
整体感知
A
B
C
D
B
A
C
D
A
B
C
D
性质探究一:(边上具备哪些性质?)
C
B
D
A
性质 探究 一
平行四边形:对边平行且相等
矩形: 对边平行且相等
菱形: 对边平行,四条边都相等
正方形:对边平行,四条边都相等
注意区别哟!
A
B
C
D
B
A
C
D
A
B
C
D
性质探究一:(角上具备哪些性质?)
C
B
D
A
平行四边形:对角相等
矩形:四个角都是直角
菱形:对角相等
正方形:四个角都是直角
性质 探究 二
A
B
C
D
O
B
O
A
C
D
A
B
C
D
O
性质探究三:(对角线上具备哪些性质?)
C
B
D
O
A
平行四边形:对角线互相平分
矩形:对角线互相平分且相等
菱形:对角线互相垂直平分,并且每条对角线平分一组对角
正方形:对角线互相垂直平分且相等,每条对 角线平分一组对角
性质 探究 三
A
B
C
D
O
B
O
A
C
D
A
B
C
D
O
性质探究四:(对称性上具备哪些性质?)
C
B
D
O
A
平行四边形:中心对称图形
矩形:中心对称图形、轴对称图形
菱形:中心对称图形、轴对称图形
正方形:中心对称图形、轴对称图形
性质 探究 四
二、几种特殊平行四边形的性质
平行
四边形
矩 形
菱 形
正方形
边
对边平行
且相等
对边平行
且相等
对边平行,四条边都相等
对边平行,
四条边
都相等
角
对角相等
四个角
都是直角
对角相等
四个角
都是直角
对 角 线
两条对角线互相平分
两条对角线互相平分且相等
两条对角线互相垂直平分,
每条对角线平分一组对角
两条对角线互相垂直平分
且相等,每条对角线平分
一组对角
对称性
中心对称
轴对称
中心对称
轴对称
中心对称
轴对称
中心对称
A
B
C
D
O
B
O
A
C
D
A
B
C
D
O
三:探索特殊平行四边形被两条对角线分成的几个三角形间的关系
C
B
D
O
A
正方形
正方形
学以致用
挑战自我
勇攀高峰
积极抢答
相信自己是最棒的!
(一)判断题:
1.平行四边形的对角线相等 ( )
2.矩形的四个角都相等 ( )
3.菱形的对角线互相垂直平分 且相等( )
4. 正方形既是平行四边形,又是矩形,又是菱形,所以它具备它们所具有的所有性质( )
5.正方形既是轴对称图形又是中心对称图形
( )
1
夯实基础,针对训练
3.如图,菱形ABCD的周长是52cm,一条对角线长是24cm,则它的面积是 _______cm.
1.如图,□ ABCD的对角线AC、BD长度之和为20cm,若△OAD的周长为17cm,则AD=____cm
2
2.矩形的一内角平分线把矩形的一条边分成3和5两部分,则该矩形的周长_________
A
B
C
D
O
7
(二)填空题:
22或26
O
A
D
C
B
120
4.如图,在菱形ABCD中,∠BAD= 60°,周长为16cm,则较短的对角线长为( )
A
A 4 √3cm B 2√3 cm
C 2 cm
D 4 cm
B
C
D
O
D
知识反馈,形成能力
2
O
讨论:用两个全等的不等边三角形纸片可以拼出几种形状不同的平行四边形?
(小结:平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。)
小组探究
6
动手画一画!
6 如图,EF过矩形ABCD对角线的交点O,且分别交于AB、CD于E、F,那么图中阴影部分的面积是矩形ABCD
A:1/5 B:1/4 C:1/3 D:3/10
的面积的( )
D
F
B
活学活用,形成技巧
3
A
B
C
O
E
如图,正方形ABCD的两条对角线相交于点O,O又是正方形EFMO的一个顶点,两个正方形的边长都为2,那么两个正方形重叠部分的面积为多少?
A
B
E
C
D
O
F
M
挑战自我!
M
N
答案:1
4 自我拓展,励志成功
A
B
E
C
D
O
F
M
答案:1
变式1:如果正方形EFMO的边长变为4,那么图中重叠部分的面积又为多少?
变式2:边长变为a呢?
A
B
E
C
D
O
F
M
思考:通过这道题,你能得出什么结论?
变式三:正方形EFMO变为任意多边形,但是满足∠EON=90度,重叠部分的面积有没有变化?
结论:无论多边形如何改变,只要∠EON=90度,重叠部分的面积就始终等于正方形ABCD面积的1/4
N
答案:1
将五个边长都是2的正方形如图摆放,点A、B、C、D、E分别是正方形的中心,则图中阴影部分的面积是__。
4
已知:如图所示,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,过A作AG⊥EB,垂足为G,AG交BD于F
求证:OE=OF
O
G
F
A
B
C
D
E
5 自我拓展,励志成功
如图,折叠矩形的一边AD,点D落在BC边上点F处,已知AB=8,BC=10,则EC的长是多少?
B
C
A
D
E
F
解:设EC=x,则DE=8-x,
由轴对称可知: EF=DE=8-x,AF=AD=10,又因AB=8,
故BF=6,故FC=BC-BF=4。
在Rt?FCE中,
42+x =(8-x) ,
解得 x=3
2
2
A
P
E
D
C
B
.
.
5.如图:菱形ABCD中AB=2,∠B=120°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是_________ .
3
√
□ABCD的周长为32cm, ∠ABC的角平分线交边AD所在直线于点E,且AE:ED
=3:2,则AB=______________.
6cm或12cm
链接中考
A
B
C
D
E
A
B
C
D
E
3x
3x
2x
x
2x
3x
如图,已知,在正方形ABCD中,E、F分别是BC,CD上的点,且∠EAF=45度.
求证:EF=BE+FD
下课了!
结束寄语
学如三角形
一角信心
一角方法
一角勤奋
三角合定,学有稳定
