2021_2022学年新教材高中数学单元复习课第4课时对数运算与对数函数课件(55张ppt)北师大版必修第一册
文档属性
| 名称 | 2021_2022学年新教材高中数学单元复习课第4课时对数运算与对数函数课件(55张ppt)北师大版必修第一册 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-04 21:22:16 | ||
图片预览









文档简介
(共55张PPT)
第4课时 对数运算与对数函数
知
识
网
络
要
点
梳
理
专题归纳·核心突破
知
识
网
络
要
点
梳
理
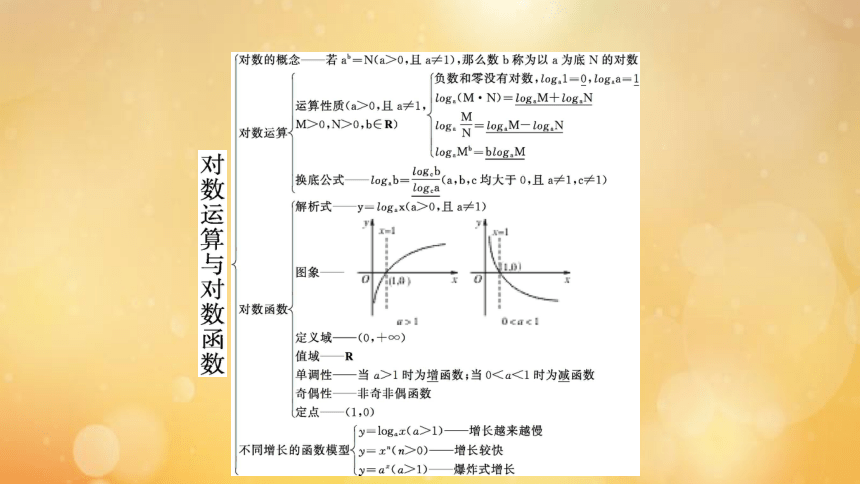
1.对数是怎样定义的?
提示:一般地,如果a(a>0,且a≠1)的b次幂等于N,即ab=N,那么数b称为以a为底N的对数,记作logaN=b,其中a叫作对数的底数,N叫作真数.
2.对数有哪些基本性质?
提示:(1)负数和零没有对数;
(2)若a>0,且a≠1,则loga1=0,logaa=1;
3.对数的运算性质有哪些?
4.对数的换底公式是怎样的?
5.对数运算的一般思路是什么?
提示:对数运算的一般思路:
(1)首先利用幂的运算把底数或真数进行变形,化成分数指数幂的形式,使幂的底数最简,然后正用对数运算性质化简合并.
(2)将对数式化为同底数对数的和、差、倍数运算,然后逆用对数的运算性质,转化为同底对数真数的积、商、幂的运算.
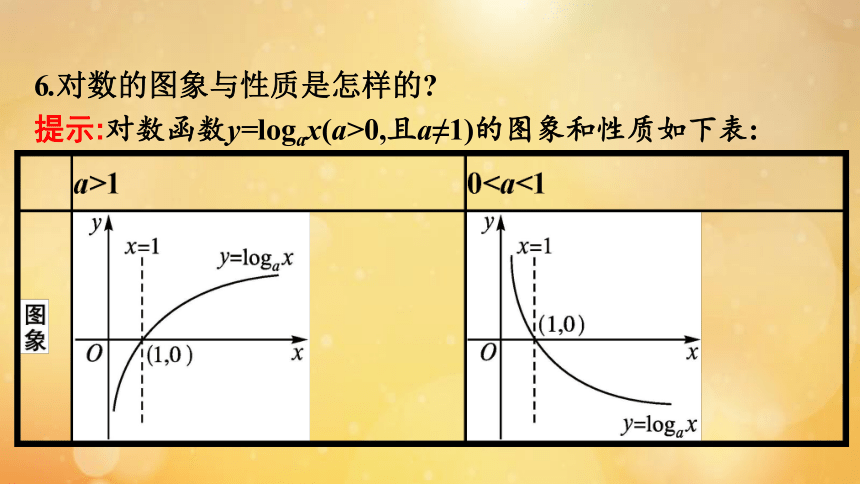
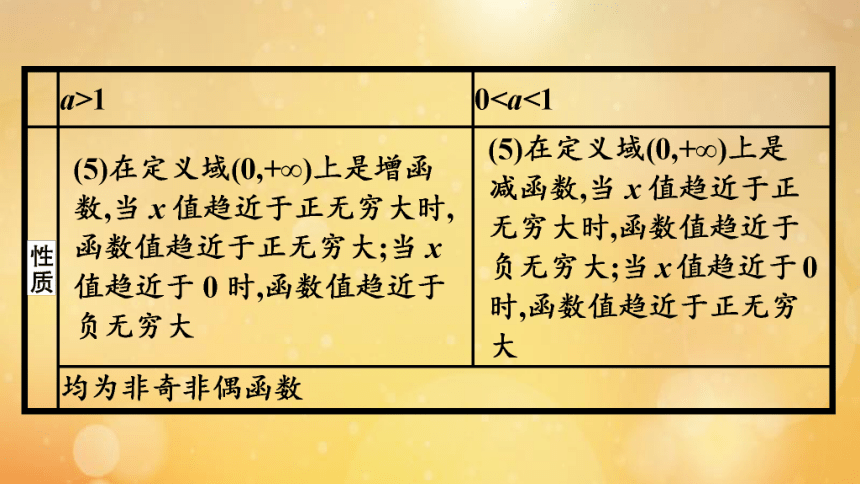
6.对数的图象与性质是怎样的?
提示:对数函数y=logax(a>0,且a≠1)的图象和性质如下表:
7.比较数的大小,常用方法有哪些?
提示:(1)比较两数(式)或几个数(式)的大小常用的方法有单调性法、图象法、中间搭桥法、作差法、作商法.
(2)当需要比较大小的两个实数均是指数幂或对数式时,可将其看成某个指数函数、对数函数或幂函数的函数值,然后利用该函数的单调性比较.
(3)比较多个数的大小时,先利用“0”和“1”作为分界点,即把它们分为“小于0”“大于等于0小于等于1”“大于1”三部分,再在各部分内利用函数的性质比较大小.
8.指数函数与对数函数的性质有什么区别和联系?
提示:指数函数、对数函数是一对“姊妹”函数,它们的定义、图象、性质、运算既有区别又有联系.
(1)指数函数y=ax(a>0,且a≠1),对数函数y=logax(a>0,且a≠1,x>0)的图象和性质都与a的取值有密切的联系,a变化时,函数的图象和性质也随之改变.
(2)指数函数y=ax(a>0,且a≠1)恒过定点(0,1),对数函数y=logax
(a>0,且a≠1,x>0)恒过定点(1,0).
(3)指数函数y=ax(a>0,且a≠1)的定义域是对数函数y=logax(a>0,且a≠1,x>0)的值域;指数函数y=ax(a>0,且a≠1)的值域是对数函数y=logax(a>0,且a≠1,x>0)的定义域.
(4)指数函数y=ax(a>0,且a≠1)和对数函数y=logax(a>0,且a≠1,
x>0)在a>1时都是增函数,在0(5)指数函数y=ax(a>0,且a≠1)与对数函数y=logax(a>0,且a≠1,
x>0)互为反函数,函数图象关于直线y=x对称.
9.指数函数模型、对数函数模型、幂函数模型,这三种函数模型的表达式及其增长特点是什么?
提示:三种函数模型的表达式及其增长特点
(1)指数函数模型:表达式为f(x)=abx+c(a,b,c为常数,a>0),当b>1时,增长特点是随着自变量x的增大,函数值增大的速度越来越快,常称之为“指数爆炸”;当0(2)对数函数模型:表达式为f(x)=mlogax+n(m,n,a为常数,m>0),当a>1时,增长的特点是开始阶段增长得较快,但随着x的逐渐增大,其函数值变化得越来越慢,常称之为“蜗牛式增长”;当0(3)幂函数模型:表达式为f(x)=axα+b(a,b,α为常数,a≠0,α≠1,
α>0),其增长情况由a和α的取值确定,常见的有一元二次函数模型.
【思考辨析】
判断下列说法是否正确,正确的在它后面的括号里画“√”,错误的画“×”.
(1)log2x2=2log2x.(
×
)
(7)函数y=log5(x+1)在区间(-1,+∞)上是增函数.(
√
)
(8)对数函数的图象一定在y轴右侧.(
√
)
(9)当01,则y=logax的函数值都大于零.(
×
)
(10)y=x10比y=1.1x的增长速度更快些.(
×
)
(11)对于任意的x>0,都有2x>log2x.(
√
)
(12)对于任意的x,都有2x>x2.(
×
)
专题归纳·核心突破
专题整合
高考体验
专题一 对数的运算
分析:利用对数的运算性质化简求值.
对数运算首先要注意公式应用过程中范围的变化,前后要等价;其次要熟练地运用对数的三个运算性质,并根据具体问题合理利用对数恒等式和换底公式等.换底公式是对数计算、化简、证明常用的公式,一定要掌握并灵活运用.
专题二 对数函数的图象
【例2】
如图,函数f(x)的图象为折线ACB,则不等式f(x)≥log2(x+1)的解集是( )
?
A.{x|-1B.{x|-1≤x≤1}
C.{x|-1D.{x|-1解析:借助函数的图象求解该不等式.
令g(x)=y=log2(x+1),在同一平面直角坐标系中画出函数f(x),
g(x)的图象如图.
即函数f(x)和g(x)的公共点为(1,1).
结合图象知不等式f(x)≥log2(x+1)的解集为{x|-1答案:C
1.函数图象是高考考查的重点内容,在历年高考中都有涉及.考查形式有知式选图、知图造式、图象变换以及用图象解题.函数图象形象地显示了函数的性质,利用数形结合有时起到事半功倍的效果.
2.研究对数型函数的图象时,一般从最基本的对数函数的图象入手,通过平移、伸缩、对称变换得到.特别地,要注意底数a>1和0【变式训练2】
若函数y=logax(a>0,且a≠1)的图象如图所示,则下列函数图象正确的是( )
解析:由题意得y=logax(a>0,且a≠1)的图象过(3,1)点,
可解得a=3.
选项B中,y=x3,由幂函数的图象可知正确;
选项C中,y=(-x)3=-x3,显然图象不符;
选项D中,y=log3(-x)的图象与y=log3x的图象关于y轴对称.显然不符.故选B.
答案:B
专题三 大小比较问题
【例3】
(1)比较大小:log1.10.7,log1.20.7;
(2)设a>0,且a≠1,若P=loga(a3+1),Q=loga(a2+1),比较P,Q的大小.
解:(1)方法1:注意到两个对数的真数相同,可先比较log0.71.1与log0.71.2的大小.
∵0<0.7<1,1.1<1.2,
∴由对数函数的单调性,得log0.71.1>log0.71.2.
又∵log0.71.1<0,log0.71.2<0,
方法2:也可以利用对数函数的图象,当底数大于1时,底数越大,在直线x=1右侧图象越靠近x轴,
由图(图略)可知log1.10.7(2)①当0即a3+1又当0∴loga(a3+1)>loga(a2+1),即P>Q.
②当a>1时,有a3>a2,即a3+1>a2+1.
又当a>1时,y=logax在区间(0,+∞)上为增函数,
∴loga(a3+1)>loga(a2+1),即P>Q.故P>Q.
比较几个数的大小,最基本的方法是将需要比较大小的实数看成某类函数的函数值,然后利用该类函数的单调性比较大小,采用中间值比较也是常用方法.
答案:C
专题四 对数函数性质的应用
【例4】
已知函数f(x)=log9(9x+1)+kx(k∈R)是偶函数.
(1)求k的值.
函数的图象是函数的重要表示方法,它具有明显的直观性,通过函数的图象能够掌握函数重要的性质,如单调性、奇偶性等.反之,掌握好函数的性质,有助于函数图象的正确画出.
【变式训练4】
已知函数f(x)=lg(ax-kbx)(k>0,a>1>b>0)的定义域为(0,+∞),问:是否存在实数a,b,使得f(x)恰在区间(1,+∞)上取正值,且f(3)=lg
4?若存在,求出a,b的值;若不存在,请说明理由.
从而k=1.故f(x)=lg(ax-bx).
若存在满足条件的实数a,b,
则f(3)=lg(a3-b3)=lg
4,
且f(x)=lg(ax-bx)>0恰在x>1时成立.
又由f(x)在区间[1,+∞)上是增函数,得当x>1时,f(x)>f(1),
所以f(1)=0,那么a-b=1.
又a3-b3=4,且a>1>b>0,
考点一 对数的概念及基本运算
1.(2018·全国Ⅰ高考)已知函数f(x)=log2(x2+a),若f(3)=1,则a= .?
解析:因为f(3)=log2(9+a)=1,
所以9+a=2,即a=-7.
答案:-7
2.(2018·全国Ⅲ高考)下列函数中,其图象与函数y=ln
x的图象关于直线x=1对称的是( )
A.y=ln(1-x)
B.y=ln(2-x)
C.y=ln(1+x)
D.y=ln(2+x)
解析:设所求函数的图象上点P(x,y)关于直线x=1对称的点为Q(2-x,y),由题意知点Q在函数y=ln
x的图象上,∴y=ln(2-x),故选B.
答案:B
考点二 对数函数的性质
且y=log2x在区间(0,+∞)上单调递增,
所以log23>log2e>log22=1,即c>a>1.
因为函数y=ln
x在区间(0,+∞)上单调递增,且b=ln
2,
所以ln
2e=1,即b<1.综上可知,c>a>b.故选D.
答案:D
4.(2018·全国Ⅲ高考)设a=log0.20.3,b=log20.3,则( )
A.a+bB.abC.a+b<0D.ab<0答案:B
5.(2019·全国Ⅲ高考改编)设f(x)是定义域为R的偶函数,且在区间(0,+∞)内单调递减,则( )
答案:C
6.(2017·天津高考)已知奇函数f(x)在R上是增函数,g(x)=xf(x).若a=g(-log25.1),b=g(20.8),c=g(3),则a,b,c的大小关系为( )
A.aB.cC.bD.b解析:∵f(x)是R上的奇函数,
∴g(x)=xf(x)是R上的偶函数.∴g(-log25.1)=g(log25.1).
∵奇函数f(x)在R上是增函数,∴g(x)在(0,+∞)上是增函数.
∵2∴g(20.8)故选C.
答案:C
答案:D
8.(2017·全国Ⅰ高考改编)已知函数f(x)=ln
x+ln(2-x),则( )
A.f(x)在区间(0,2)上单调递增
B.f(x)在区间(0,2)上单调递减
C.y=f(x)的图象关于直线x=1对称
D.y=f(x)的图象关于点(1,0)对称
解析:f(x)=ln
x+ln(2-x)=ln(-x2+2x),x∈(0,2).当x∈(0,1)时,x增大,-x2+2x增大,ln(-x2+2x)增大,当x∈(1,2)时,x增大,-x2+2x减小,ln(-x2+2x)减小,即f(x)在区间(0,1)上单调递增,在区间(1,2)上单调递减,故排除选项A,B;因为f(2-x)=ln(2-x)+ln[2-(2-x)]
=ln(2-x)+ln
x=f(x),所以y=f(x)的图象关于直线x=1对称,故排除选项D.故选C.
答案:C
9.(2017·全国Ⅱ高考)函数f(x)=ln(x2-2x-8)的单调递增区间是( )
A.(-∞,-2)
B.(-∞,1)
C.(1,+∞)
D.(4,+∞)
解析:由x2-2x-8>0,解得x<-2或x>4.故函数f(x)的定义域为(-∞,
-2)∪(4,+∞).令t=x2-2x-8,则t=x2-2x-8在区间(-∞,-2)内单调递减,在区间(4,+∞)内单调递增.又因为y=ln
t在t∈(0,+∞)内单调递增,依据复合函数单调性的同增异减原则,可得函数f(x)的单调递增区间为(4,+∞).故选D.
答案:D
(1)当a=5时,解不等式f(x)>0;
(2)若关于x的方程f(x)-log2[(a-4)x+2a-5]=0的解集中恰好有一个元素,求a的取值范围;
(3)设a>0,若对任意
,函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.
第4课时 对数运算与对数函数
知
识
网
络
要
点
梳
理
专题归纳·核心突破
知
识
网
络
要
点
梳
理
1.对数是怎样定义的?
提示:一般地,如果a(a>0,且a≠1)的b次幂等于N,即ab=N,那么数b称为以a为底N的对数,记作logaN=b,其中a叫作对数的底数,N叫作真数.
2.对数有哪些基本性质?
提示:(1)负数和零没有对数;
(2)若a>0,且a≠1,则loga1=0,logaa=1;
3.对数的运算性质有哪些?
4.对数的换底公式是怎样的?
5.对数运算的一般思路是什么?
提示:对数运算的一般思路:
(1)首先利用幂的运算把底数或真数进行变形,化成分数指数幂的形式,使幂的底数最简,然后正用对数运算性质化简合并.
(2)将对数式化为同底数对数的和、差、倍数运算,然后逆用对数的运算性质,转化为同底对数真数的积、商、幂的运算.
6.对数的图象与性质是怎样的?
提示:对数函数y=logax(a>0,且a≠1)的图象和性质如下表:
7.比较数的大小,常用方法有哪些?
提示:(1)比较两数(式)或几个数(式)的大小常用的方法有单调性法、图象法、中间搭桥法、作差法、作商法.
(2)当需要比较大小的两个实数均是指数幂或对数式时,可将其看成某个指数函数、对数函数或幂函数的函数值,然后利用该函数的单调性比较.
(3)比较多个数的大小时,先利用“0”和“1”作为分界点,即把它们分为“小于0”“大于等于0小于等于1”“大于1”三部分,再在各部分内利用函数的性质比较大小.
8.指数函数与对数函数的性质有什么区别和联系?
提示:指数函数、对数函数是一对“姊妹”函数,它们的定义、图象、性质、运算既有区别又有联系.
(1)指数函数y=ax(a>0,且a≠1),对数函数y=logax(a>0,且a≠1,x>0)的图象和性质都与a的取值有密切的联系,a变化时,函数的图象和性质也随之改变.
(2)指数函数y=ax(a>0,且a≠1)恒过定点(0,1),对数函数y=logax
(a>0,且a≠1,x>0)恒过定点(1,0).
(3)指数函数y=ax(a>0,且a≠1)的定义域是对数函数y=logax(a>0,且a≠1,x>0)的值域;指数函数y=ax(a>0,且a≠1)的值域是对数函数y=logax(a>0,且a≠1,x>0)的定义域.
(4)指数函数y=ax(a>0,且a≠1)和对数函数y=logax(a>0,且a≠1,
x>0)在a>1时都是增函数,在0
x>0)互为反函数,函数图象关于直线y=x对称.
9.指数函数模型、对数函数模型、幂函数模型,这三种函数模型的表达式及其增长特点是什么?
提示:三种函数模型的表达式及其增长特点
(1)指数函数模型:表达式为f(x)=abx+c(a,b,c为常数,a>0),当b>1时,增长特点是随着自变量x的增大,函数值增大的速度越来越快,常称之为“指数爆炸”;当0
α>0),其增长情况由a和α的取值确定,常见的有一元二次函数模型.
【思考辨析】
判断下列说法是否正确,正确的在它后面的括号里画“√”,错误的画“×”.
(1)log2x2=2log2x.(
×
)
(7)函数y=log5(x+1)在区间(-1,+∞)上是增函数.(
√
)
(8)对数函数的图象一定在y轴右侧.(
√
)
(9)当0
×
)
(10)y=x10比y=1.1x的增长速度更快些.(
×
)
(11)对于任意的x>0,都有2x>log2x.(
√
)
(12)对于任意的x,都有2x>x2.(
×
)
专题归纳·核心突破
专题整合
高考体验
专题一 对数的运算
分析:利用对数的运算性质化简求值.
对数运算首先要注意公式应用过程中范围的变化,前后要等价;其次要熟练地运用对数的三个运算性质,并根据具体问题合理利用对数恒等式和换底公式等.换底公式是对数计算、化简、证明常用的公式,一定要掌握并灵活运用.
专题二 对数函数的图象
【例2】
如图,函数f(x)的图象为折线ACB,则不等式f(x)≥log2(x+1)的解集是( )
?
A.{x|-1
C.{x|-1
令g(x)=y=log2(x+1),在同一平面直角坐标系中画出函数f(x),
g(x)的图象如图.
即函数f(x)和g(x)的公共点为(1,1).
结合图象知不等式f(x)≥log2(x+1)的解集为{x|-1
1.函数图象是高考考查的重点内容,在历年高考中都有涉及.考查形式有知式选图、知图造式、图象变换以及用图象解题.函数图象形象地显示了函数的性质,利用数形结合有时起到事半功倍的效果.
2.研究对数型函数的图象时,一般从最基本的对数函数的图象入手,通过平移、伸缩、对称变换得到.特别地,要注意底数a>1和0
若函数y=logax(a>0,且a≠1)的图象如图所示,则下列函数图象正确的是( )
解析:由题意得y=logax(a>0,且a≠1)的图象过(3,1)点,
可解得a=3.
选项B中,y=x3,由幂函数的图象可知正确;
选项C中,y=(-x)3=-x3,显然图象不符;
选项D中,y=log3(-x)的图象与y=log3x的图象关于y轴对称.显然不符.故选B.
答案:B
专题三 大小比较问题
【例3】
(1)比较大小:log1.10.7,log1.20.7;
(2)设a>0,且a≠1,若P=loga(a3+1),Q=loga(a2+1),比较P,Q的大小.
解:(1)方法1:注意到两个对数的真数相同,可先比较log0.71.1与log0.71.2的大小.
∵0<0.7<1,1.1<1.2,
∴由对数函数的单调性,得log0.71.1>log0.71.2.
又∵log0.71.1<0,log0.71.2<0,
方法2:也可以利用对数函数的图象,当底数大于1时,底数越大,在直线x=1右侧图象越靠近x轴,
由图(图略)可知log1.10.7
②当a>1时,有a3>a2,即a3+1>a2+1.
又当a>1时,y=logax在区间(0,+∞)上为增函数,
∴loga(a3+1)>loga(a2+1),即P>Q.故P>Q.
比较几个数的大小,最基本的方法是将需要比较大小的实数看成某类函数的函数值,然后利用该类函数的单调性比较大小,采用中间值比较也是常用方法.
答案:C
专题四 对数函数性质的应用
【例4】
已知函数f(x)=log9(9x+1)+kx(k∈R)是偶函数.
(1)求k的值.
函数的图象是函数的重要表示方法,它具有明显的直观性,通过函数的图象能够掌握函数重要的性质,如单调性、奇偶性等.反之,掌握好函数的性质,有助于函数图象的正确画出.
【变式训练4】
已知函数f(x)=lg(ax-kbx)(k>0,a>1>b>0)的定义域为(0,+∞),问:是否存在实数a,b,使得f(x)恰在区间(1,+∞)上取正值,且f(3)=lg
4?若存在,求出a,b的值;若不存在,请说明理由.
从而k=1.故f(x)=lg(ax-bx).
若存在满足条件的实数a,b,
则f(3)=lg(a3-b3)=lg
4,
且f(x)=lg(ax-bx)>0恰在x>1时成立.
又由f(x)在区间[1,+∞)上是增函数,得当x>1时,f(x)>f(1),
所以f(1)=0,那么a-b=1.
又a3-b3=4,且a>1>b>0,
考点一 对数的概念及基本运算
1.(2018·全国Ⅰ高考)已知函数f(x)=log2(x2+a),若f(3)=1,则a= .?
解析:因为f(3)=log2(9+a)=1,
所以9+a=2,即a=-7.
答案:-7
2.(2018·全国Ⅲ高考)下列函数中,其图象与函数y=ln
x的图象关于直线x=1对称的是( )
A.y=ln(1-x)
B.y=ln(2-x)
C.y=ln(1+x)
D.y=ln(2+x)
解析:设所求函数的图象上点P(x,y)关于直线x=1对称的点为Q(2-x,y),由题意知点Q在函数y=ln
x的图象上,∴y=ln(2-x),故选B.
答案:B
考点二 对数函数的性质
且y=log2x在区间(0,+∞)上单调递增,
所以log23>log2e>log22=1,即c>a>1.
因为函数y=ln
x在区间(0,+∞)上单调递增,且b=ln
2,
所以ln
2
答案:D
4.(2018·全国Ⅲ高考)设a=log0.20.3,b=log20.3,则( )
A.a+b
5.(2019·全国Ⅲ高考改编)设f(x)是定义域为R的偶函数,且在区间(0,+∞)内单调递减,则( )
答案:C
6.(2017·天津高考)已知奇函数f(x)在R上是增函数,g(x)=xf(x).若a=g(-log25.1),b=g(20.8),c=g(3),则a,b,c的大小关系为( )
A.a
∴g(x)=xf(x)是R上的偶函数.∴g(-log25.1)=g(log25.1).
∵奇函数f(x)在R上是增函数,∴g(x)在(0,+∞)上是增函数.
∵2
答案:C
答案:D
8.(2017·全国Ⅰ高考改编)已知函数f(x)=ln
x+ln(2-x),则( )
A.f(x)在区间(0,2)上单调递增
B.f(x)在区间(0,2)上单调递减
C.y=f(x)的图象关于直线x=1对称
D.y=f(x)的图象关于点(1,0)对称
解析:f(x)=ln
x+ln(2-x)=ln(-x2+2x),x∈(0,2).当x∈(0,1)时,x增大,-x2+2x增大,ln(-x2+2x)增大,当x∈(1,2)时,x增大,-x2+2x减小,ln(-x2+2x)减小,即f(x)在区间(0,1)上单调递增,在区间(1,2)上单调递减,故排除选项A,B;因为f(2-x)=ln(2-x)+ln[2-(2-x)]
=ln(2-x)+ln
x=f(x),所以y=f(x)的图象关于直线x=1对称,故排除选项D.故选C.
答案:C
9.(2017·全国Ⅱ高考)函数f(x)=ln(x2-2x-8)的单调递增区间是( )
A.(-∞,-2)
B.(-∞,1)
C.(1,+∞)
D.(4,+∞)
解析:由x2-2x-8>0,解得x<-2或x>4.故函数f(x)的定义域为(-∞,
-2)∪(4,+∞).令t=x2-2x-8,则t=x2-2x-8在区间(-∞,-2)内单调递减,在区间(4,+∞)内单调递增.又因为y=ln
t在t∈(0,+∞)内单调递增,依据复合函数单调性的同增异减原则,可得函数f(x)的单调递增区间为(4,+∞).故选D.
答案:D
(1)当a=5时,解不等式f(x)>0;
(2)若关于x的方程f(x)-log2[(a-4)x+2a-5]=0的解集中恰好有一个元素,求a的取值范围;
(3)设a>0,若对任意
,函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
