湖南省长沙市广益实验中学2020-2021学年九年级下学期第三次限时检测数学试卷(word版含解析)
文档属性
| 名称 | 湖南省长沙市广益实验中学2020-2021学年九年级下学期第三次限时检测数学试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 638.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-04 22:35:01 | ||
图片预览

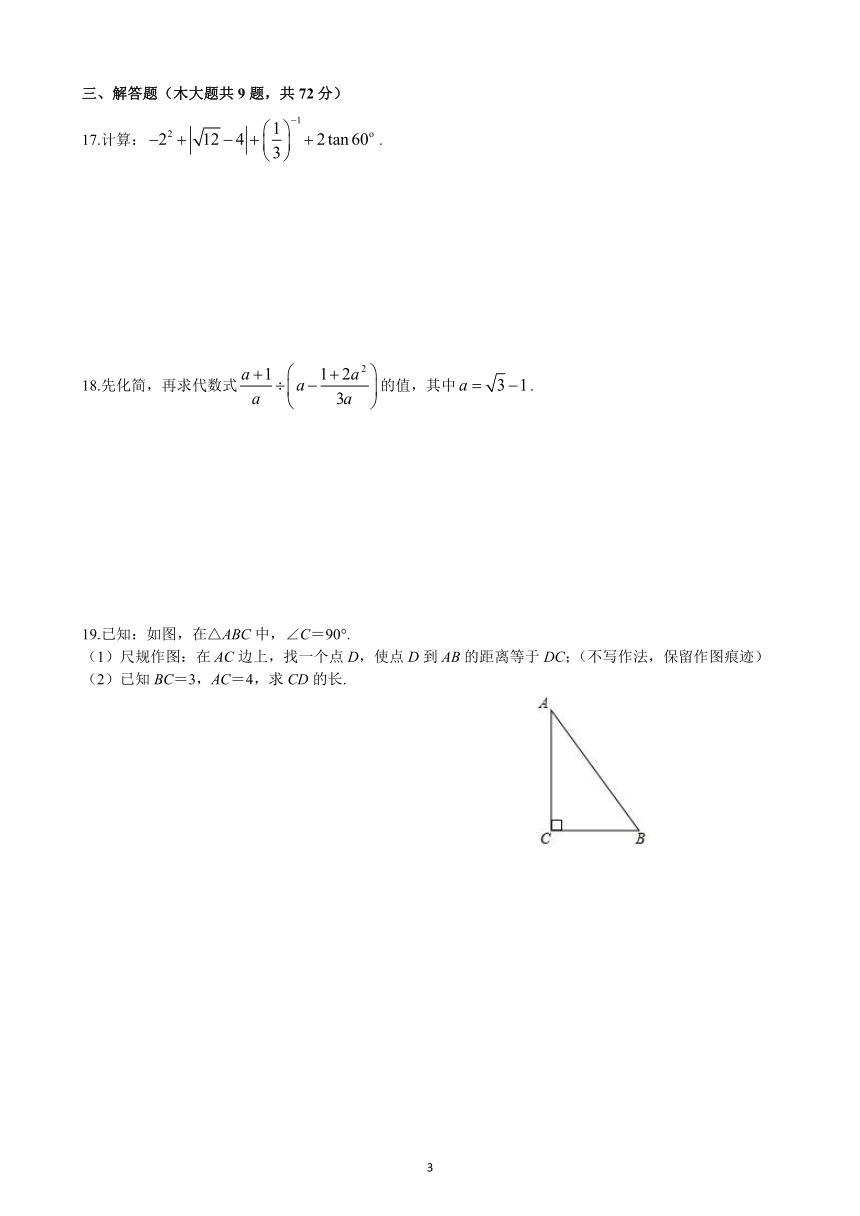

文档简介
2020-2021学年湖南省长沙市广益实验中学九年级(下)第三次限时检测数学试卷
一、选择题(本大题共12小题,共36分)
1.下列电视台的台标,是中心对称图形的是( )
2.下列运算正确的是( )
A.
B.
C.
D.
3.人体内的冠状病毒最早在英国被分离出来,2013年世界卫生组织命名被发现的“中东呼吸系统综合征冠
状病毒(新型冠状病毒)”呈球形或椭圆形,一次研究发现的新型冠状病毒直径为177纳米(1纳米=
米),那么此新型冠状病毒的直径为( )
A.厘米
B.厘米
C.厘米
D.厘米
4.已知⊙O的半径等于3,圆心O到直线l的距离为5,那么直线l与⊙O的位置关系是( )
A.直线l与⊙O相交
B.直线l与⊙O相离
C.直线l与⊙O相切
D.无法确定
5.下列事件中,是必然事件的是( )
A.从一个只有红球的盒子里摸出一个球是红球
B.买一张电影票,座位号是5的倍数
C.掷一枚质地均匀的硬币,正面向上
D.走过一个红绿灯路口时,前方正好是红灯
6.一组数据:1、2、2、3,若添加一个数据2,则发生变化的统计量是( )
A.平均数
B.中位数
C.众数
D.方差
7.若是关于x的一元二次方程的两个根,且,则b的值为( )
A.
B.3
C.
D.5
8.若圆锥的主视图是边长为4cm的等边三角形,则该圆锥俯视图的面积是( )
A.4πcm2
B.8πcm2
C.12πcm2
D.16πcm2
9.我国古代数学著作《九章算术》记载了一道“牛马问题”:“今有二马、一牛价过一万,如半马之价.一
马、二牛价不满一万,如半牛之价.问牛、马价各几何.”其大意为:现有两匹马加一头牛的价钱超过一
万,超过的部分正好是半匹马的价钱;一匹马加上二头牛的价钱则不到一万,不足部分正好是半头牛的价
钱,求一匹马、一头牛各多少钱?设一匹马价钱为x元,一头牛价钱为y元,则符合题意的方程组是( )
A.
B.
C.
D.
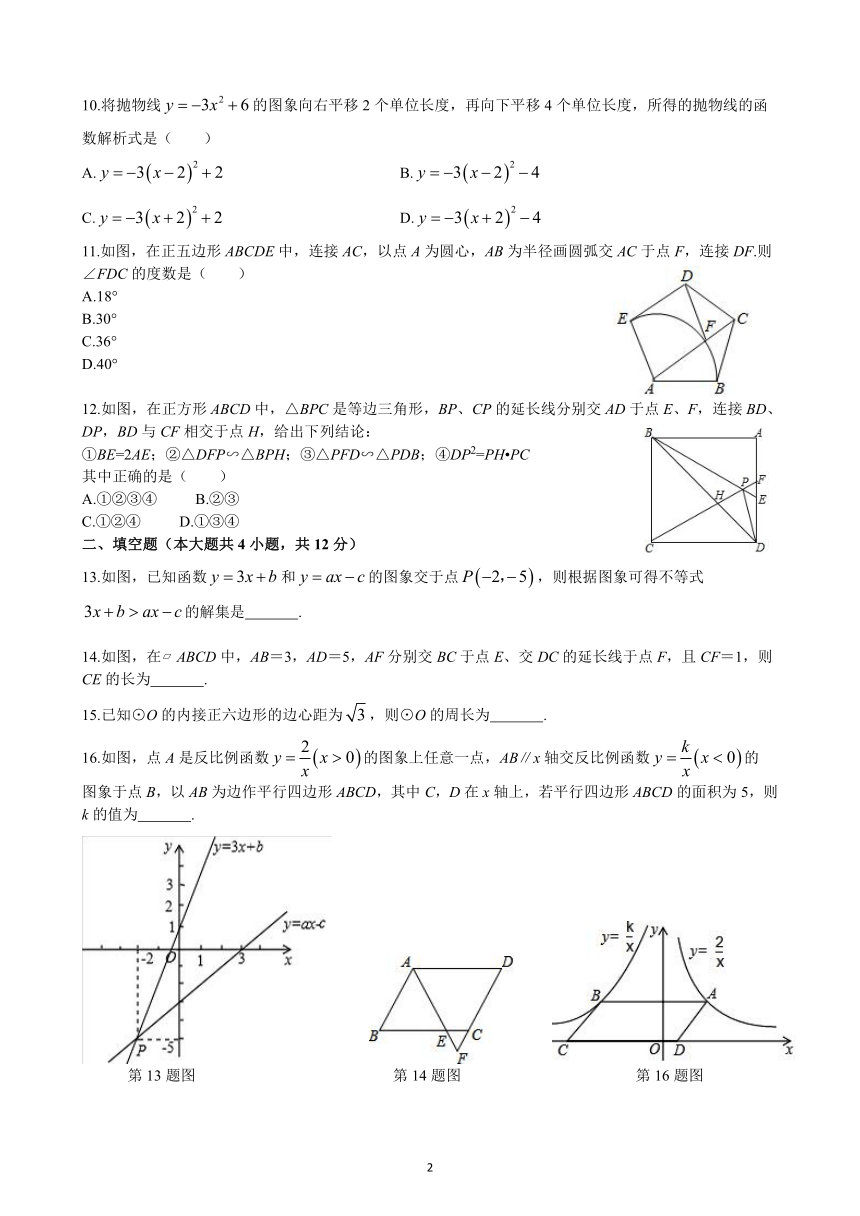
10.将抛物线的图象向右平移2个单位长度,再向下平移4个单位长度,所得的抛物线的函
数解析式是( )
A.
B.
C.
D.
11.如图,在正五边形ABCDE中,连接AC,以点A为圆心,AB为半径画圆弧交AC于点F,连接DF.则
∠FDC的度数是( )
A.18°
B.30°
C.36°
D.40°
12.如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、
DP,BD与CF相交于点H,给出下列结论:
①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PH?PC
其中正确的是( )
A.①②③④
B.②③
C.①②④
D.①③④
二、填空题(本大题共4小题,共12分)
13.如图,已知函数和的图象交于点,则根据图象可得不等式
的解集是
.
14.如图,在?ABCD中,AB=3,AD=5,AF分别交BC于点E、交DC的延长线于点F,且CF=1,则
CE的长为
.
15.已知⊙O的内接正六边形的边心距为,则⊙O的周长为
.
16.如图,点A是反比例函数的图象上任意一点,AB∥x轴交反比例函数的
图象于点B,以AB为边作平行四边形ABCD,其中C,D在x轴上,若平行四边形ABCD的面积为5,则
k的值为
.
第13题图
第14题图
第16题图
三、解答题(木大题共9题,共72分)
17.计算:.
18.先化简,再求代数式的值,其中.
19.已知:如图,在△ABC中,∠C=90°.
(1)尺规作图:在AC边上,找一个点D,使点D到AB的距离等于DC;(不写作法,保留作图痕迹)
(2)已知BC=3,AC=4,求CD的长.
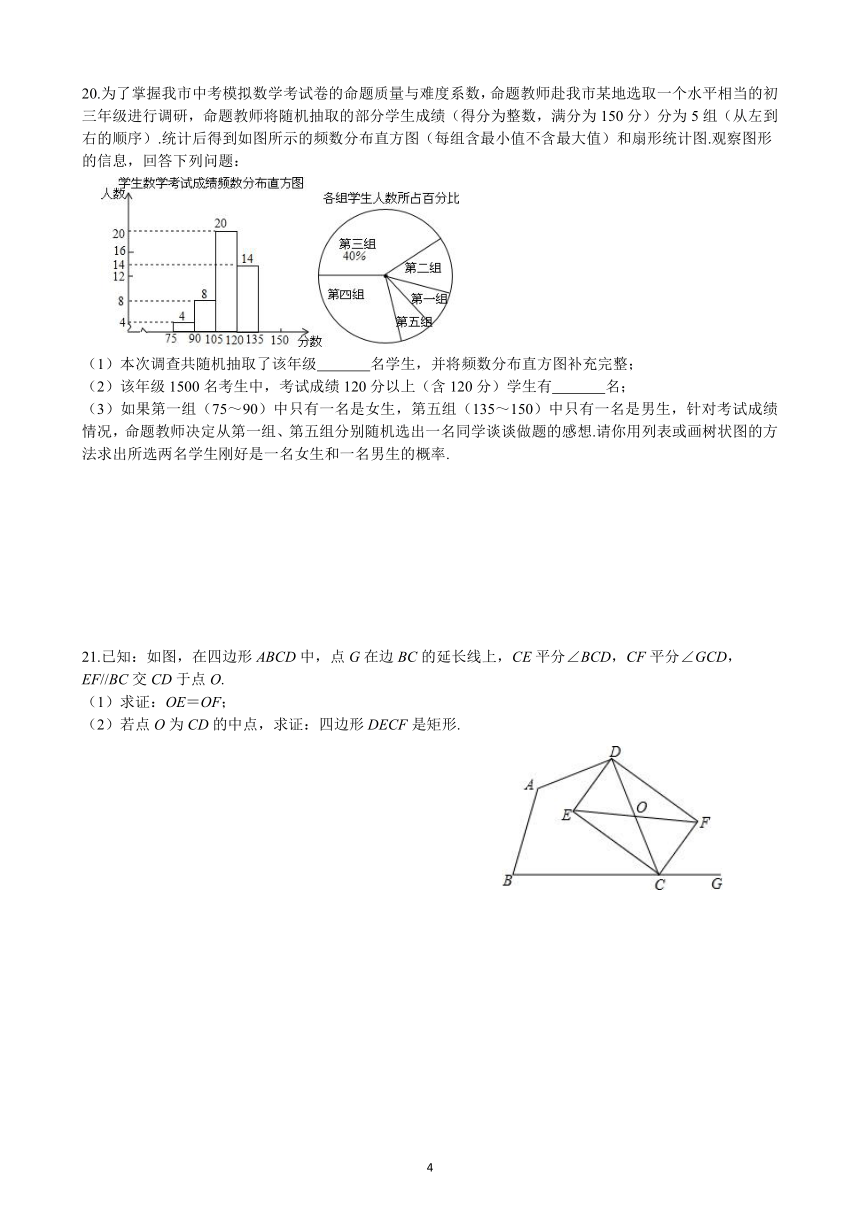
20.为了掌握我市中考模拟数学考试卷的命题质量与难度系数,命题教师赴我市某地选取一个水平相当的初
三年级进行调研,命题教师将随机抽取的部分学生成绩(得分为整数,满分为150分)分为5组(从左到
右的顺序).统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.观察图形
的信息,回答下列问题:
(1)本次调查共随机抽取了该年级
名学生,并将频数分布直方图补充完整;
(2)该年级1500名考生中,考试成绩120分以上(含120分)学生有
名;
(3)如果第一组(75~90)中只有一名是女生,第五组(135~150)中只有一名是男生,针对考试成绩情况,命题教师决定从第一组、第五组分别随机选出一名同学谈谈做题的感想.请你用列表或画树状图的方法求出所选两名学生刚好是一名女生和一名男生的概率.
21.已知:如图,在四边形ABCD中,点G在边BC的延长线上,CE平分∠BCD,CF平分∠GCD,
EF//BC交CD于点O.
(1)求证:OE=OF;
(2)若点O为CD的中点,求证:四边形DECF是矩形.
22.如图,一个圆形喷水池的中央垂直于水面安装了一个柱形喷水装置OA,O恰好在水面中心,安置在柱
子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,
按如图所示建立直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式可以用
表示,且抛物线经过点.
请根据以上信息,解答下列问题;
(1)求抛物线的函数关系式,并确定喷水装置OA的高度;
(2)喷出的水流距水面的最大高度是多少米?
(3)若不计其他因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外?
23.如图,在Rt△ABC中,∠ACB=90°,点D在边AC上,∠DBC=∠BAC,⊙O经过A、B、D
三点,连接DO并延长交⊙O于点E,连接AE,DE与AB交于点F.
(1)求证:CB是⊙O的切线;
(2)求证:AB=EB;
(3)若DF=3,EF=7,求BC的长.
24.定义:若一次函数与反比例函数存在两个不同的公共点,则称函数
为一次函数与反比例函数的“生成函数”.
(1)判断一次函数与反比例函数是否存在“生成函数”,若存在,请写出“生成函数”,若不存在,请说明理由.
(2)若一次函数与反比例函数交于两点,连接AB、AO、BO(O为坐标原点),若△AOB的面积为2b,求与的“生成函数”.
(3)若一次函数与反比例函数的“生成函数”经过且与x轴交于C、D两点,与y轴交于点E,其中,求△CDE面积S的取值范围.
25.如图,在平面直角坐标系中,直线与x轴,y轴分别交于A、B两点,将直线l
沿x轴翻折交y轴于点C,连接AC,过点B作BD⊥AC垂足为点D,并交x轴于点E.
(1)当∠BAO=30°时,求直线l解析式及点E坐标;
(2)若AB=2BE,求S△ABC;
(3)在(2)问条件下,构造抛物线y1,y2,其中抛物线y1经过A、B、E三点,其二次项系数为m;抛物线同时满足以下三个条件:①过线段OE中点;②;③当时,函数y2有最大值m;求a的值.
2020-2021学年湖南省长沙市雨花区广益实验中学九年级(下)第三次限时检测数学试卷
参考答案与试题解析
一、选择题(本大题共12小题,共36分)
1.下列电视台的台标,是中心对称图形的是( )
A.
B.
C.
D.
【解答】解:A、不是中心对称图形,故A选项错误;
B、不是中心对称图形,故B选项错误;
C、不是中心对称图形,故C选项错误;
D、是中心对称图形,故D选项正确.
故选:D.
2.下列运算正确的是( )
A.3a﹣a=2
B.(a2)3=a5
C.a2?a3=a5
D.a6÷a3=a2
【解答】解:A、3a﹣a=2a,故此选项错误;
B、(a2)3=a6,故此选项错误;
C、a2?a3=a5,正确;
D、a6÷a3=a3,故此选项错误;
故选:C.
3.人体内的冠状病毒最早在英国被分离出来,2013年世界卫生组织命名被发现的“中东呼吸系统综合征冠状病毒(新型冠状病毒)”呈球形或椭圆形,一次研究发现的新型冠状病毒直径为177纳米(1纳米=10﹣9米),那么此新型冠状病毒的直径为( )
A.177×10﹣9厘米
B.177×10﹣7厘米
C.1.77×10﹣7厘米
D.1.77×10﹣5厘米
【解答】解:177纳米=177×10﹣9米=1.77×10﹣7米=1.77×10﹣5厘米.
故选:D.
4.已知⊙O的半径等于3,圆心O到直线l的距离为5,那么直线l与⊙O的位置关系是( )
A.直线l与⊙O相交
B.直线l与⊙O相离
C.直线l与⊙O相切
D.无法确定
【解答】解:∵⊙O的半径等于3,圆心O到直线l的距离为5,3<5,
∴直线l与⊙O相离.
故选:B.
5.下列事件中,是必然事件的是( )
A.从一个只有红球的盒子里摸出一个球是红球
B.买一张电影票,座位号是5的倍数
C.掷一枚质地均匀的硬币,正面向上
D.走过一个红绿灯路口时,前方正好是红灯
【解答】解:A、从一个只有红球的盒子里摸出一个球是红球,是必然事件;
B、买一张电影票,座位号是5的倍数,是随机事件;
C、掷一枚质地均匀的硬币,正面向上,是随机事件;
D、走过一个红绿灯路口时,前方正好是红灯,是随机事件.
故选:A.
6.一组数据:1、2、2、3,若添加一个数据2,则发生变化的统计量是( )
A.平均数
B.中位数
C.众数
D.方差
【解答】解:A、原来数据的平均数是2,添加数字2后平均数仍为2,故A与要求不符;
B、原来数据的中位数是2,添加数字2后中位数仍为2,故B与要求不符;
C、原来数据的众数是2,添加数字2后众数仍为2,故C与要求不符;
D、原来数据的方差==,
添加数字2后的方差==,故方差发生了变化.
故选:D.
7.若x1,x2是关于x的一元二次方程x2+bx﹣4=0的两个根,x1x2﹣x1﹣x2=﹣7且,则b的值为( )
A.﹣3
B.3
C.﹣5
D.5
【解答】解:由题意得,x1+x2=﹣b,x1x2=﹣4,
∴x1x2﹣x1﹣x2=x1x2﹣(x1+x2)=﹣4+b=﹣7,
∴b=﹣3,
故选:A.
8.若圆锥的主视图是边长为4cm的等边三角形,则该圆锥俯视图的面积是( )
A.4πcm2
B.8πcm2
C.12πcm2
D.16πcm2
【解答】解:∵圆锥的主视图是边长为4的等边三角形,
∴圆锥俯视图圆的直径是4,
则该圆锥俯视图的面积是π×22=4π,
故选:A.
9.我国古代数学著作《九章算术》记载了一道“牛马问题”:“今有二马、一牛价过一万,如半马之价.一马、二牛价不满一万,如半牛之价.问牛、马价各几何.”其大意为:现有两匹马加一头牛的价钱超过一万,超过的部分正好是半匹马的价钱;一匹马加上二头牛的价钱则不到一万,不足部分正好是半头牛的价钱,求一匹马、一头牛各多少钱?设一匹马价钱为x元,一头牛价钱为y元,则符合题意的方程组是( )
A.
B.
C.
D.
【解答】解:依题意得:.
故选:A.
10.将抛物线y=﹣3x2+6的图象向右平移2个单位长度,再向下平移4个单位长度,所得的抛物线的函数解析式是( )
A.y=﹣3(x﹣2)2+2
B.y=﹣3(x﹣2)2﹣4
C.y=﹣3(x+2)2+2
D.y=﹣3(x+2)2﹣4
【解答】解:将抛物线y=﹣3x2+6的图象向右平移2个单位长度,再向下平移4个单位长度后,得到的抛物线的解析式为y=﹣3(x﹣2)2+6﹣4,即y=﹣3(x﹣2)2+2,
故选:A.
11.如图,在正五边形ABCDE中,连接AC,以点A为圆心,AB为半径画圆弧交AC于点F,连接DF.则∠FDC的度数是( )
A.18°
B.30°
C.36°
D.40°
【解答】解:∵五边形ABCDE是正五边形,
∴∠AED=∠EAB=∠ABC=108°,
∵BA=BC,
∴∠BAC=∠BCA=36°,
∴∠EAC=72°,
∴∠AED+∠EAC=180°,
∴DE∥AF,
∵AE=AF=DE,
∴四边形AEDF是菱形,
∴∠EDF=∠EAF=72°,
∵∠EDC=108°,
∴∠FDC=36°,
故选:C.
12.如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:
①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PH?PC
其中正确的是( )
A.①②③④
B.②③
C.①②④
D.①③④
【解答】解:∵△BPC是等边三角形,
∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,
在正方形ABCD中,
∵AB=BC=CD,∠A=∠ADC=∠BCD=90°
∴∠ABE=∠DCF=30°,
∴BE=2AE;故①正确;
∵PC=CD,∠PCD=30°,
∴∠PDC=75°,
∴∠FDP=15°,
∵∠DBA=45°,
∴∠PBD=15°,
∴∠FDP=∠PBD,
∵∠DFP=∠BPC=60°,
∴△DFP∽△BPH;故②正确;
∵∠FDP=∠PBD=15°,∠ADB=45°,
∴∠PDB=30°,而∠DFP=60°,
∴∠PFD≠∠PDB,
∴△PFD与△PDB不会相似;故③错误;
∵∠PDH=∠PCD=30°,∠DPH=∠DPC,
∴△DPH∽△CPD,
∴,
∴DP2=PH?PC,故④正确;
故选:C.
二、填空题(本大题共4小题,共12分)
13.如图,已知函数y=3x+b和y=ax﹣c的图象交于点P(﹣2,﹣5),则根据图象可得不等式3x+b>ax﹣c的解集是 x>﹣2 .
【解答】解:∵函数y=3x+b和y=ax﹣c的图象交于点P(﹣2,﹣5),
则根据图象可得不等3x+b>ax﹣c的解集是x>﹣2,
故答案为:x>﹣2.
14.如图,在?ABCD中,AB=3,AD=5,AF分别交BC于点E、交DC的延长线于点F,且CF=1,则CE的长为 .
【解答】解:∵四边形ABCD是平行四边形
∴AB∥CD,AD=BC=5,
∴△ABE∽△FCE
∴==3
∴BE=3CE
∵BC=BE+CE=5
∴CE=
故答案为:
15.已知⊙O的内接正六边形的边心距为,则⊙O的周长为 4π .
【解答】解:如图所示,连接OA、OB,
∵多边形ABCDEF是正六边形,
∴∠AOB=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴∠OAM=60°,
∴OM=OA?sin∠OAM,
∴OA===2,
∴⊙O的周长为4π,
故答案为:4π.
16.如图,点A是反比例函数y=(x>0)的图象上任意一点,AB∥x轴交反比例函数y=(x<0)的图象于点B,以AB为边作平行四边形ABCD,其中C,D在x轴上,若平行四边形ABCD的面积为5,则k的值为 ﹣3 .
【解答】解:过点B作BM⊥x轴,过点A作AN⊥x轴,则∠BMC=∠AND=90°,
∵四边形ABCD为平行四边形,
∴BC∥AD,BC=AD,
∴∠BCM=∠ADN,
在△BCM和△ADN中
∴△BCM≌△ADN,
∴S?BCDA=S矩形BMNA=5,
又∵S矩形BMNA=﹣k+2=5,
∴k=﹣3.
故答案为:﹣3.
三、解答题(木大题共9题,共72分)
17.(6分)计算:.
【解答】解:原式=﹣4+|2﹣4|++2×
=﹣4+4﹣2+3+2
=3.
18.(6分)先化简,再求代数式÷(a﹣)的值,其中a=﹣1.
【解答】解:原式=÷
=?
=,
当a=﹣1时,
原式=
=﹣6﹣3.
19.(6分)已知:如图,在△ABC中,∠C=90°.
(1)尺规作图:在AC边上,找一个点D,使点D到AB的距离等于DC;(不写作法,保留作图痕迹)
(2)已知BC=3,AC=4,求CD的长.
【解答】解:(1)如图,点D即为所求.
在Rt△ACB中,∵BC=3,AC=4,
∴AB===5,
∵∠DCE=∠DEC=90°,∠CBD=∠EBD,BD=BD,
∴△CBD≌△EBD(AAS),
∴CD=DE,BC=BE=3,设CD=DE=m,
在Rt△ADE中,∵AD2=AE2+DE2,
∴(4﹣m)2=m2+22,
解得m=,
∴CD=.
20.(8分)为了掌握我市中考模拟数学考试卷的命题质量与难度系数,命题教师赴我市某地选取一个水平相当的初三年级进行调研,命题教师将随机抽取的部分学生成绩(得分为整数,满分为150分)分为5组(从左到右的顺序).统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.观察图形的信息,回答下列问题:
(1)本次调查共随机抽取了该年级 50 名学生,并将频数分布直方图补充完整;
(2)该年级1500名考生中,考试成绩120分以上(含120分)学生有 540 名;
(3)如果第一组(75~90)中只有一名是女生,第五组(135~150)中只有一名是男生,针对考试成绩情况,命题教师决定从第一组、第五组分别随机选出一名同学谈谈做题的感想.请你用列表或画树状图的方法求出所选两名学生刚好是一名女生和一名男生的概率.
【解答】解:(1)20÷40%=50,
所以本次调查共随机抽取了该年级50名学生,
第五组的学生数为50﹣4﹣8﹣20﹣14=14,
频数分布直方图补充为:
(2)1500×=540,
所以该年级1500名考生中,考试成绩120分以上(含120分)学生估计有540名;
故答案为50,540;
(3)画树状图为:
共有16种等可能的结果数,其中所选两名学生刚好是一名女生和一名男生的结果数为10,
所以所选两名学生刚好是一名女生和一名男生的概率==.
21.(8分)已知:如图,在四边形ABCD中,点G在边BC的延长线上,CE平分∠BCD,CF平分∠GCD,EF∥BC交CD于点O.
(1)求证:OE=OF;
(2)若点O为CD的中点,求证:四边形DECF是矩形.
【解答】证明:(1)∵CE平分∠BCD、CF平分∠GCD,
∴∠BCE=∠DCE,∠DCF=∠GCF,(1分)
∵EF∥BC,
∴∠BCE=∠FEC,∠EFC=∠GCF,(1分)
∴∠DCE=∠FEC,∠EFC=∠DCF,(1分)
∴OE=OC,OF=OC,
∴OE=OF;(2分)
(2)∵点O为CD的中点,
∴OD=OC,
又OE=OF,
∴四边形DECF是平行四边形,(2分)
∵CE平分∠BCD、CF平分∠GCD,
∴,(2分)
∴,(2分)
即∠ECF=90°,
∴四边形DECF是矩形.(1分)
22.(9分)如图,一个圆形喷水池的中央垂直于水面安装了一个柱形喷水装置OA,O恰好在水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,按如图所示建立直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式可以用y=﹣x2+bx+c表示,且抛物线经过点B(,),C(2,).
请根据以上信息,解答下列问题;
(1)求抛物线的函数关系式,并确定喷水装置OA的高度;
(2)喷出的水流距水面的最大高度是多少米?
(3)若不计其他因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外?
【解答】解:(1)根据题意,将点B(,),C(2,)代入y=﹣x2+bx+c,
得:,
解得:,
∴y与x的函数关系式为:y=﹣x2+2x+,
当x=0时,y=,
∴喷水装置OA的高度为米;
(2)∵y=﹣x2+2x+=﹣(x﹣1)2+,
∴当x=1时,y取得最大值,
故喷出的水流距水面的最大高度是米;
(3)当y=0时,解方程﹣x2+2x+=0,
解得:x1=1﹣,x2=1+,
∵x1=1﹣<0,不合题意,舍去,
∴x2=1+,
答:水池的半径至少要1+米,才能使喷出的水流不至于落在池外.
23.(9分)如图,在Rt△ABC中,∠ACB=90°,点D在边AC上,∠DBC=∠BAC,⊙O经过A、B、D三点,连接DO并延长交⊙O于点E,连接AE,DE与AB交于点F.
(1)求证:CB是⊙O的切线;
(2)求证:AB=EB;
(3)若DF=3,EF=7,求BC的长.
【解答】(1)证明:在⊙O中,OB=OD,∠BAC=∠BED,
∴∠ODB=∠OBD,
∵∠DBC=∠BAC,
∴∠DBC=∠BED,
∵DE是⊙O的直径,
∴∠DBE=90°,
∴∠ODB+∠BED=90°,
∴∠OBD+∠DBC=90°,
∴OB⊥BC,
∵OB是⊙O的半径,
∴CB是⊙O的切线;
(2)证明:在⊙O中,∠ABD=∠AED,
由(1)得:∠DBC=∠BED,
∴∠ABD+∠DBC=∠AED+∠BED,
∴∠ABC=∠BEA,
∵DE是⊙O的直径,
∴∠EAC=90°,
∵∠ACB=90°,
∴∠EAC+∠ACB=180°,
∴AE∥BC,
∴∠ABC=∠BAE,
∴∠BEA=∠BAE,
∴AB=EB;
(3)解:延长BO交AE于H,
由∠HAC=∠ACB=∠OBC=90°,得四边形ACBH是矩形,
∴OH⊥AE,
∴BC=AH=AE,
∵DF=3,EF=7,
∴直径DE=10,
即半径DO=EO=5,
∴OF=2,
∵OB∥AC,
∴=,
∴AD=,
在Rt△ADE中,AE==,
∴BC=AH=AE=.
24.(10分)定义:若一次函数y=ax+b与反比例函数y=﹣存在两个不同的公共点,则称函数y=ax2+bx+c为一次函数y=ax+b与反比例函数y=﹣的“生成函数”.
(1)判断一次函数y=﹣x+5与反比例函数y=﹣是否存在“生成函数”,若存在,请写出“生成函数”,若不存在,请说明理由.
(2)若一次函数y=x﹣b(b>0)与反比例函数y=交于A(x1,y1)、B(x2,y2)(x1<x2)两点,连接AB、AO、BO(O为坐标原点),若△AOB的面积为2b,求y=x﹣b与y=的“生成函数”.
(3)若一次函数y=ax+b与反比例函数y=的“生成函数”经过(1,﹣1)且与x轴交于C、D两点,与y轴交于点E,其中a>b>0,求△CDE面积S的取值范围.
【解答】解:(1)将y=﹣x+5代入y=﹣中,整理,得:x2﹣5x+﹣6=0,
∵△=(﹣5)2﹣4×1×(﹣6)=49>0,
∴一次函数y=﹣x+5与反比例函数y=﹣存在两个不同的公共点,
∴一次函数y=﹣x+5与反比例函数y=﹣的“生成函数”为y=﹣x2+5x+6.
(2)设直线AB与x轴交于点M,则点M的坐标为(b,0).
将y=x﹣b代入y=中,整理,得:x2﹣bx﹣2=0,
∴x1+x2=b,x1x2=﹣2,
∴x2﹣x1==,
∴y2﹣y1=x2﹣x1=,
∴S△AOB=OM?(y2﹣y1)=b?=2b,
解得:b=2或b=﹣2(舍去),
∴y=x﹣b与y=的“生成函数”为y=x2﹣2x﹣2.
(3)y=ax+b与y=的“生成函数”为y=ax2+bx﹣3,
∴点E的坐标为(0,﹣3).
∵该函数经过点(1,﹣1),
∴a+b﹣3=﹣1,
∴a+b=2.
当y=0时,有ax2+bx﹣3=0,
∴xC+xD=﹣,xCxD=﹣,
∴|xC﹣xD|======,
∴S=OE?|xC﹣xD|=.
∵a>b>0,a+b=2,
∴1<<2,
∴<S<.
25.(10分)如图,在平面直角坐标系中,直线l:y=kx﹣8k(k<0)与x轴,y轴分别交于A、B两点,将直线l沿x轴翻折交y轴于点C,连接AC,过点B作BD⊥AC垂足为点D,并交x轴于点E.
(1)当∠BAO=30°时,求直线l解析式及点E坐标;
(2)若AB=2BE,求S△ABC;
(3)在(2)问条件下,构造抛物线y1,y2,其中抛物线y1经过A、B、E三点,其二次项系数为m;抛物线y2=ax2+bx+c同时满足以下三个条件:①过线段OE中点;②5a+3b+2c=0;③当≤x≤时,函数y2有最大值m;求a的值.
【解答】解:(1)∵y=kx﹣8k(k<0)与x轴,y轴分别交于A、B两点,
∴点A(8,0),点B(0,﹣8k)
∵∠BAO=30°
∴tan∠BAO==
即=
∴k=﹣
即点B(0,),BO=
∴直线解析式y=﹣x+
∵将直线l沿x轴翻折交y轴于点C
∴AC=AB,∠BAO=∠CAO=30°
∴∠BAC=60°
∴△ABC是等边三角形,且BD⊥AC
∴∠CBD=30°=∠ABD
∴BO=OE
∴OE=
∴点E(,0)
(2)∵翻折
∴∠BAO=∠CAO,OB=OC
∵AO⊥BO,BD⊥AC
∴∠OBE+∠BEO=90°,∠CAO+∠AED=90°
∴∠OBE=∠CAO=∠BAO
且∠AOB=∠AOB
∴△BOE∽△AOB
∴,且AB=2BE
∴
∴OB=4=OC
∴BC=OB+OC=8
∴S△ABC=×8×8=32
(3)∵△BOE∽△AOB
∴
∴OE=2,OB=4
∴点A(8,0),点B(0,4),点E(2,0)
∵抛物线y1经过A、B、E三点,其二次项系数为m;
∴设y1=m(x﹣2)(x﹣8)过点B
∴4=16m
∴m=
∵点O(0,0),点E(2,0)
∴线段OE的中点(1,0)
∵抛物线y2=ax2+bx+c过线段OE中点;且5a+3b+2c=0;
∴
解得:
∴抛物线y2=ax2+bx+c=ax2﹣3ax+2a=a(x﹣1)(x﹣2)
∴对称轴为直线x=
∵当≤x≤时,函数y2有最大值m;
∴当≤x≤2时,函数y2有最大值;
若a>0时,当x=时,函数y2有最大值.
∴a(﹣1)(﹣2)=
∴a=
若a<0时,当x=,函数y2有最大值.
∴a(﹣1)(﹣2)=
∴a=﹣1
综上所述:a=﹣或﹣1
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2021/4/18
18:53:52;用户:980383396;邮箱:980383396@;学号:10028921
一、选择题(本大题共12小题,共36分)
1.下列电视台的台标,是中心对称图形的是( )
2.下列运算正确的是( )
A.
B.
C.
D.
3.人体内的冠状病毒最早在英国被分离出来,2013年世界卫生组织命名被发现的“中东呼吸系统综合征冠
状病毒(新型冠状病毒)”呈球形或椭圆形,一次研究发现的新型冠状病毒直径为177纳米(1纳米=
米),那么此新型冠状病毒的直径为( )
A.厘米
B.厘米
C.厘米
D.厘米
4.已知⊙O的半径等于3,圆心O到直线l的距离为5,那么直线l与⊙O的位置关系是( )
A.直线l与⊙O相交
B.直线l与⊙O相离
C.直线l与⊙O相切
D.无法确定
5.下列事件中,是必然事件的是( )
A.从一个只有红球的盒子里摸出一个球是红球
B.买一张电影票,座位号是5的倍数
C.掷一枚质地均匀的硬币,正面向上
D.走过一个红绿灯路口时,前方正好是红灯
6.一组数据:1、2、2、3,若添加一个数据2,则发生变化的统计量是( )
A.平均数
B.中位数
C.众数
D.方差
7.若是关于x的一元二次方程的两个根,且,则b的值为( )
A.
B.3
C.
D.5
8.若圆锥的主视图是边长为4cm的等边三角形,则该圆锥俯视图的面积是( )
A.4πcm2
B.8πcm2
C.12πcm2
D.16πcm2
9.我国古代数学著作《九章算术》记载了一道“牛马问题”:“今有二马、一牛价过一万,如半马之价.一
马、二牛价不满一万,如半牛之价.问牛、马价各几何.”其大意为:现有两匹马加一头牛的价钱超过一
万,超过的部分正好是半匹马的价钱;一匹马加上二头牛的价钱则不到一万,不足部分正好是半头牛的价
钱,求一匹马、一头牛各多少钱?设一匹马价钱为x元,一头牛价钱为y元,则符合题意的方程组是( )
A.
B.
C.
D.
10.将抛物线的图象向右平移2个单位长度,再向下平移4个单位长度,所得的抛物线的函
数解析式是( )
A.
B.
C.
D.
11.如图,在正五边形ABCDE中,连接AC,以点A为圆心,AB为半径画圆弧交AC于点F,连接DF.则
∠FDC的度数是( )
A.18°
B.30°
C.36°
D.40°
12.如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、
DP,BD与CF相交于点H,给出下列结论:
①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PH?PC
其中正确的是( )
A.①②③④
B.②③
C.①②④
D.①③④
二、填空题(本大题共4小题,共12分)
13.如图,已知函数和的图象交于点,则根据图象可得不等式
的解集是
.
14.如图,在?ABCD中,AB=3,AD=5,AF分别交BC于点E、交DC的延长线于点F,且CF=1,则
CE的长为
.
15.已知⊙O的内接正六边形的边心距为,则⊙O的周长为
.
16.如图,点A是反比例函数的图象上任意一点,AB∥x轴交反比例函数的
图象于点B,以AB为边作平行四边形ABCD,其中C,D在x轴上,若平行四边形ABCD的面积为5,则
k的值为
.
第13题图
第14题图
第16题图
三、解答题(木大题共9题,共72分)
17.计算:.
18.先化简,再求代数式的值,其中.
19.已知:如图,在△ABC中,∠C=90°.
(1)尺规作图:在AC边上,找一个点D,使点D到AB的距离等于DC;(不写作法,保留作图痕迹)
(2)已知BC=3,AC=4,求CD的长.
20.为了掌握我市中考模拟数学考试卷的命题质量与难度系数,命题教师赴我市某地选取一个水平相当的初
三年级进行调研,命题教师将随机抽取的部分学生成绩(得分为整数,满分为150分)分为5组(从左到
右的顺序).统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.观察图形
的信息,回答下列问题:
(1)本次调查共随机抽取了该年级
名学生,并将频数分布直方图补充完整;
(2)该年级1500名考生中,考试成绩120分以上(含120分)学生有
名;
(3)如果第一组(75~90)中只有一名是女生,第五组(135~150)中只有一名是男生,针对考试成绩情况,命题教师决定从第一组、第五组分别随机选出一名同学谈谈做题的感想.请你用列表或画树状图的方法求出所选两名学生刚好是一名女生和一名男生的概率.
21.已知:如图,在四边形ABCD中,点G在边BC的延长线上,CE平分∠BCD,CF平分∠GCD,
EF//BC交CD于点O.
(1)求证:OE=OF;
(2)若点O为CD的中点,求证:四边形DECF是矩形.
22.如图,一个圆形喷水池的中央垂直于水面安装了一个柱形喷水装置OA,O恰好在水面中心,安置在柱
子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,
按如图所示建立直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式可以用
表示,且抛物线经过点.
请根据以上信息,解答下列问题;
(1)求抛物线的函数关系式,并确定喷水装置OA的高度;
(2)喷出的水流距水面的最大高度是多少米?
(3)若不计其他因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外?
23.如图,在Rt△ABC中,∠ACB=90°,点D在边AC上,∠DBC=∠BAC,⊙O经过A、B、D
三点,连接DO并延长交⊙O于点E,连接AE,DE与AB交于点F.
(1)求证:CB是⊙O的切线;
(2)求证:AB=EB;
(3)若DF=3,EF=7,求BC的长.
24.定义:若一次函数与反比例函数存在两个不同的公共点,则称函数
为一次函数与反比例函数的“生成函数”.
(1)判断一次函数与反比例函数是否存在“生成函数”,若存在,请写出“生成函数”,若不存在,请说明理由.
(2)若一次函数与反比例函数交于两点,连接AB、AO、BO(O为坐标原点),若△AOB的面积为2b,求与的“生成函数”.
(3)若一次函数与反比例函数的“生成函数”经过且与x轴交于C、D两点,与y轴交于点E,其中,求△CDE面积S的取值范围.
25.如图,在平面直角坐标系中,直线与x轴,y轴分别交于A、B两点,将直线l
沿x轴翻折交y轴于点C,连接AC,过点B作BD⊥AC垂足为点D,并交x轴于点E.
(1)当∠BAO=30°时,求直线l解析式及点E坐标;
(2)若AB=2BE,求S△ABC;
(3)在(2)问条件下,构造抛物线y1,y2,其中抛物线y1经过A、B、E三点,其二次项系数为m;抛物线同时满足以下三个条件:①过线段OE中点;②;③当时,函数y2有最大值m;求a的值.
2020-2021学年湖南省长沙市雨花区广益实验中学九年级(下)第三次限时检测数学试卷
参考答案与试题解析
一、选择题(本大题共12小题,共36分)
1.下列电视台的台标,是中心对称图形的是( )
A.
B.
C.
D.
【解答】解:A、不是中心对称图形,故A选项错误;
B、不是中心对称图形,故B选项错误;
C、不是中心对称图形,故C选项错误;
D、是中心对称图形,故D选项正确.
故选:D.
2.下列运算正确的是( )
A.3a﹣a=2
B.(a2)3=a5
C.a2?a3=a5
D.a6÷a3=a2
【解答】解:A、3a﹣a=2a,故此选项错误;
B、(a2)3=a6,故此选项错误;
C、a2?a3=a5,正确;
D、a6÷a3=a3,故此选项错误;
故选:C.
3.人体内的冠状病毒最早在英国被分离出来,2013年世界卫生组织命名被发现的“中东呼吸系统综合征冠状病毒(新型冠状病毒)”呈球形或椭圆形,一次研究发现的新型冠状病毒直径为177纳米(1纳米=10﹣9米),那么此新型冠状病毒的直径为( )
A.177×10﹣9厘米
B.177×10﹣7厘米
C.1.77×10﹣7厘米
D.1.77×10﹣5厘米
【解答】解:177纳米=177×10﹣9米=1.77×10﹣7米=1.77×10﹣5厘米.
故选:D.
4.已知⊙O的半径等于3,圆心O到直线l的距离为5,那么直线l与⊙O的位置关系是( )
A.直线l与⊙O相交
B.直线l与⊙O相离
C.直线l与⊙O相切
D.无法确定
【解答】解:∵⊙O的半径等于3,圆心O到直线l的距离为5,3<5,
∴直线l与⊙O相离.
故选:B.
5.下列事件中,是必然事件的是( )
A.从一个只有红球的盒子里摸出一个球是红球
B.买一张电影票,座位号是5的倍数
C.掷一枚质地均匀的硬币,正面向上
D.走过一个红绿灯路口时,前方正好是红灯
【解答】解:A、从一个只有红球的盒子里摸出一个球是红球,是必然事件;
B、买一张电影票,座位号是5的倍数,是随机事件;
C、掷一枚质地均匀的硬币,正面向上,是随机事件;
D、走过一个红绿灯路口时,前方正好是红灯,是随机事件.
故选:A.
6.一组数据:1、2、2、3,若添加一个数据2,则发生变化的统计量是( )
A.平均数
B.中位数
C.众数
D.方差
【解答】解:A、原来数据的平均数是2,添加数字2后平均数仍为2,故A与要求不符;
B、原来数据的中位数是2,添加数字2后中位数仍为2,故B与要求不符;
C、原来数据的众数是2,添加数字2后众数仍为2,故C与要求不符;
D、原来数据的方差==,
添加数字2后的方差==,故方差发生了变化.
故选:D.
7.若x1,x2是关于x的一元二次方程x2+bx﹣4=0的两个根,x1x2﹣x1﹣x2=﹣7且,则b的值为( )
A.﹣3
B.3
C.﹣5
D.5
【解答】解:由题意得,x1+x2=﹣b,x1x2=﹣4,
∴x1x2﹣x1﹣x2=x1x2﹣(x1+x2)=﹣4+b=﹣7,
∴b=﹣3,
故选:A.
8.若圆锥的主视图是边长为4cm的等边三角形,则该圆锥俯视图的面积是( )
A.4πcm2
B.8πcm2
C.12πcm2
D.16πcm2
【解答】解:∵圆锥的主视图是边长为4的等边三角形,
∴圆锥俯视图圆的直径是4,
则该圆锥俯视图的面积是π×22=4π,
故选:A.
9.我国古代数学著作《九章算术》记载了一道“牛马问题”:“今有二马、一牛价过一万,如半马之价.一马、二牛价不满一万,如半牛之价.问牛、马价各几何.”其大意为:现有两匹马加一头牛的价钱超过一万,超过的部分正好是半匹马的价钱;一匹马加上二头牛的价钱则不到一万,不足部分正好是半头牛的价钱,求一匹马、一头牛各多少钱?设一匹马价钱为x元,一头牛价钱为y元,则符合题意的方程组是( )
A.
B.
C.
D.
【解答】解:依题意得:.
故选:A.
10.将抛物线y=﹣3x2+6的图象向右平移2个单位长度,再向下平移4个单位长度,所得的抛物线的函数解析式是( )
A.y=﹣3(x﹣2)2+2
B.y=﹣3(x﹣2)2﹣4
C.y=﹣3(x+2)2+2
D.y=﹣3(x+2)2﹣4
【解答】解:将抛物线y=﹣3x2+6的图象向右平移2个单位长度,再向下平移4个单位长度后,得到的抛物线的解析式为y=﹣3(x﹣2)2+6﹣4,即y=﹣3(x﹣2)2+2,
故选:A.
11.如图,在正五边形ABCDE中,连接AC,以点A为圆心,AB为半径画圆弧交AC于点F,连接DF.则∠FDC的度数是( )
A.18°
B.30°
C.36°
D.40°
【解答】解:∵五边形ABCDE是正五边形,
∴∠AED=∠EAB=∠ABC=108°,
∵BA=BC,
∴∠BAC=∠BCA=36°,
∴∠EAC=72°,
∴∠AED+∠EAC=180°,
∴DE∥AF,
∵AE=AF=DE,
∴四边形AEDF是菱形,
∴∠EDF=∠EAF=72°,
∵∠EDC=108°,
∴∠FDC=36°,
故选:C.
12.如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:
①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PH?PC
其中正确的是( )
A.①②③④
B.②③
C.①②④
D.①③④
【解答】解:∵△BPC是等边三角形,
∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,
在正方形ABCD中,
∵AB=BC=CD,∠A=∠ADC=∠BCD=90°
∴∠ABE=∠DCF=30°,
∴BE=2AE;故①正确;
∵PC=CD,∠PCD=30°,
∴∠PDC=75°,
∴∠FDP=15°,
∵∠DBA=45°,
∴∠PBD=15°,
∴∠FDP=∠PBD,
∵∠DFP=∠BPC=60°,
∴△DFP∽△BPH;故②正确;
∵∠FDP=∠PBD=15°,∠ADB=45°,
∴∠PDB=30°,而∠DFP=60°,
∴∠PFD≠∠PDB,
∴△PFD与△PDB不会相似;故③错误;
∵∠PDH=∠PCD=30°,∠DPH=∠DPC,
∴△DPH∽△CPD,
∴,
∴DP2=PH?PC,故④正确;
故选:C.
二、填空题(本大题共4小题,共12分)
13.如图,已知函数y=3x+b和y=ax﹣c的图象交于点P(﹣2,﹣5),则根据图象可得不等式3x+b>ax﹣c的解集是 x>﹣2 .
【解答】解:∵函数y=3x+b和y=ax﹣c的图象交于点P(﹣2,﹣5),
则根据图象可得不等3x+b>ax﹣c的解集是x>﹣2,
故答案为:x>﹣2.
14.如图,在?ABCD中,AB=3,AD=5,AF分别交BC于点E、交DC的延长线于点F,且CF=1,则CE的长为 .
【解答】解:∵四边形ABCD是平行四边形
∴AB∥CD,AD=BC=5,
∴△ABE∽△FCE
∴==3
∴BE=3CE
∵BC=BE+CE=5
∴CE=
故答案为:
15.已知⊙O的内接正六边形的边心距为,则⊙O的周长为 4π .
【解答】解:如图所示,连接OA、OB,
∵多边形ABCDEF是正六边形,
∴∠AOB=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴∠OAM=60°,
∴OM=OA?sin∠OAM,
∴OA===2,
∴⊙O的周长为4π,
故答案为:4π.
16.如图,点A是反比例函数y=(x>0)的图象上任意一点,AB∥x轴交反比例函数y=(x<0)的图象于点B,以AB为边作平行四边形ABCD,其中C,D在x轴上,若平行四边形ABCD的面积为5,则k的值为 ﹣3 .
【解答】解:过点B作BM⊥x轴,过点A作AN⊥x轴,则∠BMC=∠AND=90°,
∵四边形ABCD为平行四边形,
∴BC∥AD,BC=AD,
∴∠BCM=∠ADN,
在△BCM和△ADN中
∴△BCM≌△ADN,
∴S?BCDA=S矩形BMNA=5,
又∵S矩形BMNA=﹣k+2=5,
∴k=﹣3.
故答案为:﹣3.
三、解答题(木大题共9题,共72分)
17.(6分)计算:.
【解答】解:原式=﹣4+|2﹣4|++2×
=﹣4+4﹣2+3+2
=3.
18.(6分)先化简,再求代数式÷(a﹣)的值,其中a=﹣1.
【解答】解:原式=÷
=?
=,
当a=﹣1时,
原式=
=﹣6﹣3.
19.(6分)已知:如图,在△ABC中,∠C=90°.
(1)尺规作图:在AC边上,找一个点D,使点D到AB的距离等于DC;(不写作法,保留作图痕迹)
(2)已知BC=3,AC=4,求CD的长.
【解答】解:(1)如图,点D即为所求.
在Rt△ACB中,∵BC=3,AC=4,
∴AB===5,
∵∠DCE=∠DEC=90°,∠CBD=∠EBD,BD=BD,
∴△CBD≌△EBD(AAS),
∴CD=DE,BC=BE=3,设CD=DE=m,
在Rt△ADE中,∵AD2=AE2+DE2,
∴(4﹣m)2=m2+22,
解得m=,
∴CD=.
20.(8分)为了掌握我市中考模拟数学考试卷的命题质量与难度系数,命题教师赴我市某地选取一个水平相当的初三年级进行调研,命题教师将随机抽取的部分学生成绩(得分为整数,满分为150分)分为5组(从左到右的顺序).统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.观察图形的信息,回答下列问题:
(1)本次调查共随机抽取了该年级 50 名学生,并将频数分布直方图补充完整;
(2)该年级1500名考生中,考试成绩120分以上(含120分)学生有 540 名;
(3)如果第一组(75~90)中只有一名是女生,第五组(135~150)中只有一名是男生,针对考试成绩情况,命题教师决定从第一组、第五组分别随机选出一名同学谈谈做题的感想.请你用列表或画树状图的方法求出所选两名学生刚好是一名女生和一名男生的概率.
【解答】解:(1)20÷40%=50,
所以本次调查共随机抽取了该年级50名学生,
第五组的学生数为50﹣4﹣8﹣20﹣14=14,
频数分布直方图补充为:
(2)1500×=540,
所以该年级1500名考生中,考试成绩120分以上(含120分)学生估计有540名;
故答案为50,540;
(3)画树状图为:
共有16种等可能的结果数,其中所选两名学生刚好是一名女生和一名男生的结果数为10,
所以所选两名学生刚好是一名女生和一名男生的概率==.
21.(8分)已知:如图,在四边形ABCD中,点G在边BC的延长线上,CE平分∠BCD,CF平分∠GCD,EF∥BC交CD于点O.
(1)求证:OE=OF;
(2)若点O为CD的中点,求证:四边形DECF是矩形.
【解答】证明:(1)∵CE平分∠BCD、CF平分∠GCD,
∴∠BCE=∠DCE,∠DCF=∠GCF,(1分)
∵EF∥BC,
∴∠BCE=∠FEC,∠EFC=∠GCF,(1分)
∴∠DCE=∠FEC,∠EFC=∠DCF,(1分)
∴OE=OC,OF=OC,
∴OE=OF;(2分)
(2)∵点O为CD的中点,
∴OD=OC,
又OE=OF,
∴四边形DECF是平行四边形,(2分)
∵CE平分∠BCD、CF平分∠GCD,
∴,(2分)
∴,(2分)
即∠ECF=90°,
∴四边形DECF是矩形.(1分)
22.(9分)如图,一个圆形喷水池的中央垂直于水面安装了一个柱形喷水装置OA,O恰好在水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,按如图所示建立直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式可以用y=﹣x2+bx+c表示,且抛物线经过点B(,),C(2,).
请根据以上信息,解答下列问题;
(1)求抛物线的函数关系式,并确定喷水装置OA的高度;
(2)喷出的水流距水面的最大高度是多少米?
(3)若不计其他因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外?
【解答】解:(1)根据题意,将点B(,),C(2,)代入y=﹣x2+bx+c,
得:,
解得:,
∴y与x的函数关系式为:y=﹣x2+2x+,
当x=0时,y=,
∴喷水装置OA的高度为米;
(2)∵y=﹣x2+2x+=﹣(x﹣1)2+,
∴当x=1时,y取得最大值,
故喷出的水流距水面的最大高度是米;
(3)当y=0时,解方程﹣x2+2x+=0,
解得:x1=1﹣,x2=1+,
∵x1=1﹣<0,不合题意,舍去,
∴x2=1+,
答:水池的半径至少要1+米,才能使喷出的水流不至于落在池外.
23.(9分)如图,在Rt△ABC中,∠ACB=90°,点D在边AC上,∠DBC=∠BAC,⊙O经过A、B、D三点,连接DO并延长交⊙O于点E,连接AE,DE与AB交于点F.
(1)求证:CB是⊙O的切线;
(2)求证:AB=EB;
(3)若DF=3,EF=7,求BC的长.
【解答】(1)证明:在⊙O中,OB=OD,∠BAC=∠BED,
∴∠ODB=∠OBD,
∵∠DBC=∠BAC,
∴∠DBC=∠BED,
∵DE是⊙O的直径,
∴∠DBE=90°,
∴∠ODB+∠BED=90°,
∴∠OBD+∠DBC=90°,
∴OB⊥BC,
∵OB是⊙O的半径,
∴CB是⊙O的切线;
(2)证明:在⊙O中,∠ABD=∠AED,
由(1)得:∠DBC=∠BED,
∴∠ABD+∠DBC=∠AED+∠BED,
∴∠ABC=∠BEA,
∵DE是⊙O的直径,
∴∠EAC=90°,
∵∠ACB=90°,
∴∠EAC+∠ACB=180°,
∴AE∥BC,
∴∠ABC=∠BAE,
∴∠BEA=∠BAE,
∴AB=EB;
(3)解:延长BO交AE于H,
由∠HAC=∠ACB=∠OBC=90°,得四边形ACBH是矩形,
∴OH⊥AE,
∴BC=AH=AE,
∵DF=3,EF=7,
∴直径DE=10,
即半径DO=EO=5,
∴OF=2,
∵OB∥AC,
∴=,
∴AD=,
在Rt△ADE中,AE==,
∴BC=AH=AE=.
24.(10分)定义:若一次函数y=ax+b与反比例函数y=﹣存在两个不同的公共点,则称函数y=ax2+bx+c为一次函数y=ax+b与反比例函数y=﹣的“生成函数”.
(1)判断一次函数y=﹣x+5与反比例函数y=﹣是否存在“生成函数”,若存在,请写出“生成函数”,若不存在,请说明理由.
(2)若一次函数y=x﹣b(b>0)与反比例函数y=交于A(x1,y1)、B(x2,y2)(x1<x2)两点,连接AB、AO、BO(O为坐标原点),若△AOB的面积为2b,求y=x﹣b与y=的“生成函数”.
(3)若一次函数y=ax+b与反比例函数y=的“生成函数”经过(1,﹣1)且与x轴交于C、D两点,与y轴交于点E,其中a>b>0,求△CDE面积S的取值范围.
【解答】解:(1)将y=﹣x+5代入y=﹣中,整理,得:x2﹣5x+﹣6=0,
∵△=(﹣5)2﹣4×1×(﹣6)=49>0,
∴一次函数y=﹣x+5与反比例函数y=﹣存在两个不同的公共点,
∴一次函数y=﹣x+5与反比例函数y=﹣的“生成函数”为y=﹣x2+5x+6.
(2)设直线AB与x轴交于点M,则点M的坐标为(b,0).
将y=x﹣b代入y=中,整理,得:x2﹣bx﹣2=0,
∴x1+x2=b,x1x2=﹣2,
∴x2﹣x1==,
∴y2﹣y1=x2﹣x1=,
∴S△AOB=OM?(y2﹣y1)=b?=2b,
解得:b=2或b=﹣2(舍去),
∴y=x﹣b与y=的“生成函数”为y=x2﹣2x﹣2.
(3)y=ax+b与y=的“生成函数”为y=ax2+bx﹣3,
∴点E的坐标为(0,﹣3).
∵该函数经过点(1,﹣1),
∴a+b﹣3=﹣1,
∴a+b=2.
当y=0时,有ax2+bx﹣3=0,
∴xC+xD=﹣,xCxD=﹣,
∴|xC﹣xD|======,
∴S=OE?|xC﹣xD|=.
∵a>b>0,a+b=2,
∴1<<2,
∴<S<.
25.(10分)如图,在平面直角坐标系中,直线l:y=kx﹣8k(k<0)与x轴,y轴分别交于A、B两点,将直线l沿x轴翻折交y轴于点C,连接AC,过点B作BD⊥AC垂足为点D,并交x轴于点E.
(1)当∠BAO=30°时,求直线l解析式及点E坐标;
(2)若AB=2BE,求S△ABC;
(3)在(2)问条件下,构造抛物线y1,y2,其中抛物线y1经过A、B、E三点,其二次项系数为m;抛物线y2=ax2+bx+c同时满足以下三个条件:①过线段OE中点;②5a+3b+2c=0;③当≤x≤时,函数y2有最大值m;求a的值.
【解答】解:(1)∵y=kx﹣8k(k<0)与x轴,y轴分别交于A、B两点,
∴点A(8,0),点B(0,﹣8k)
∵∠BAO=30°
∴tan∠BAO==
即=
∴k=﹣
即点B(0,),BO=
∴直线解析式y=﹣x+
∵将直线l沿x轴翻折交y轴于点C
∴AC=AB,∠BAO=∠CAO=30°
∴∠BAC=60°
∴△ABC是等边三角形,且BD⊥AC
∴∠CBD=30°=∠ABD
∴BO=OE
∴OE=
∴点E(,0)
(2)∵翻折
∴∠BAO=∠CAO,OB=OC
∵AO⊥BO,BD⊥AC
∴∠OBE+∠BEO=90°,∠CAO+∠AED=90°
∴∠OBE=∠CAO=∠BAO
且∠AOB=∠AOB
∴△BOE∽△AOB
∴,且AB=2BE
∴
∴OB=4=OC
∴BC=OB+OC=8
∴S△ABC=×8×8=32
(3)∵△BOE∽△AOB
∴
∴OE=2,OB=4
∴点A(8,0),点B(0,4),点E(2,0)
∵抛物线y1经过A、B、E三点,其二次项系数为m;
∴设y1=m(x﹣2)(x﹣8)过点B
∴4=16m
∴m=
∵点O(0,0),点E(2,0)
∴线段OE的中点(1,0)
∵抛物线y2=ax2+bx+c过线段OE中点;且5a+3b+2c=0;
∴
解得:
∴抛物线y2=ax2+bx+c=ax2﹣3ax+2a=a(x﹣1)(x﹣2)
∴对称轴为直线x=
∵当≤x≤时,函数y2有最大值m;
∴当≤x≤2时,函数y2有最大值;
若a>0时,当x=时,函数y2有最大值.
∴a(﹣1)(﹣2)=
∴a=
若a<0时,当x=,函数y2有最大值.
∴a(﹣1)(﹣2)=
∴a=﹣1
综上所述:a=﹣或﹣1
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2021/4/18
18:53:52;用户:980383396;邮箱:980383396@;学号:10028921
同课章节目录
