_湖南省娄底涟源市2020-2021学年九年级下学期第一次月考数学试卷(word版含解析)
文档属性
| 名称 | _湖南省娄底涟源市2020-2021学年九年级下学期第一次月考数学试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 253.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-04 22:39:51 | ||
图片预览


文档简介
2020-2021学年湖南省娄底涟源市九年级(下)第一次月考数学试卷
一.选择题(共12小题,每小题3分,共36分)
1.嫦娥五号从月球风驰电掣般返回地球的速度接近第二宇宙速度,即112000米/秒,数字112000用科学记数法表示为( )
A.112×103
B.1.12×103
C.1.12×105
D.1.12×106
2.若代数式有意义,则实数x的取值范围是( )
A.x>0
B.x≥0
C.x>0且x≠2
D.x≥0且x≠2
3.已知﹣5xay与2x2yb为同类项,则a﹣b的值为( )
A.1
B.2
C.3
D.4
4.多项式8a3b2+12a3bc﹣4a2b中,各项的公因式是( )
A.a2b
B.﹣4a2b2
C.4a2b
D.﹣a2b
5.不等式组的解集是( )
A.﹣1<x≤2
B.﹣2≤x<1
C.x<﹣1或x≥2
D.2≤x<﹣1
6.在海上,灯塔位于一艘船的北偏东40度方向,那么这艘船位于这个灯塔的( )
A.南偏西40度方向
B.南偏西50度方向
C.北偏东50度方向
D.北偏东40度方向
7.设等腰三角形的一边长为5,另一边长为10,则其周长为( )
A.15
B.20
C.25
D.20或25
8.在平面直角坐标系内,将点A(1,2)先向右平移2个单位长度,再向下平移1个单位长度,则平移后所得点的坐标是( )
A.(3,1)
B.(3,3)
C.(﹣1,1)
D.(﹣1,3)
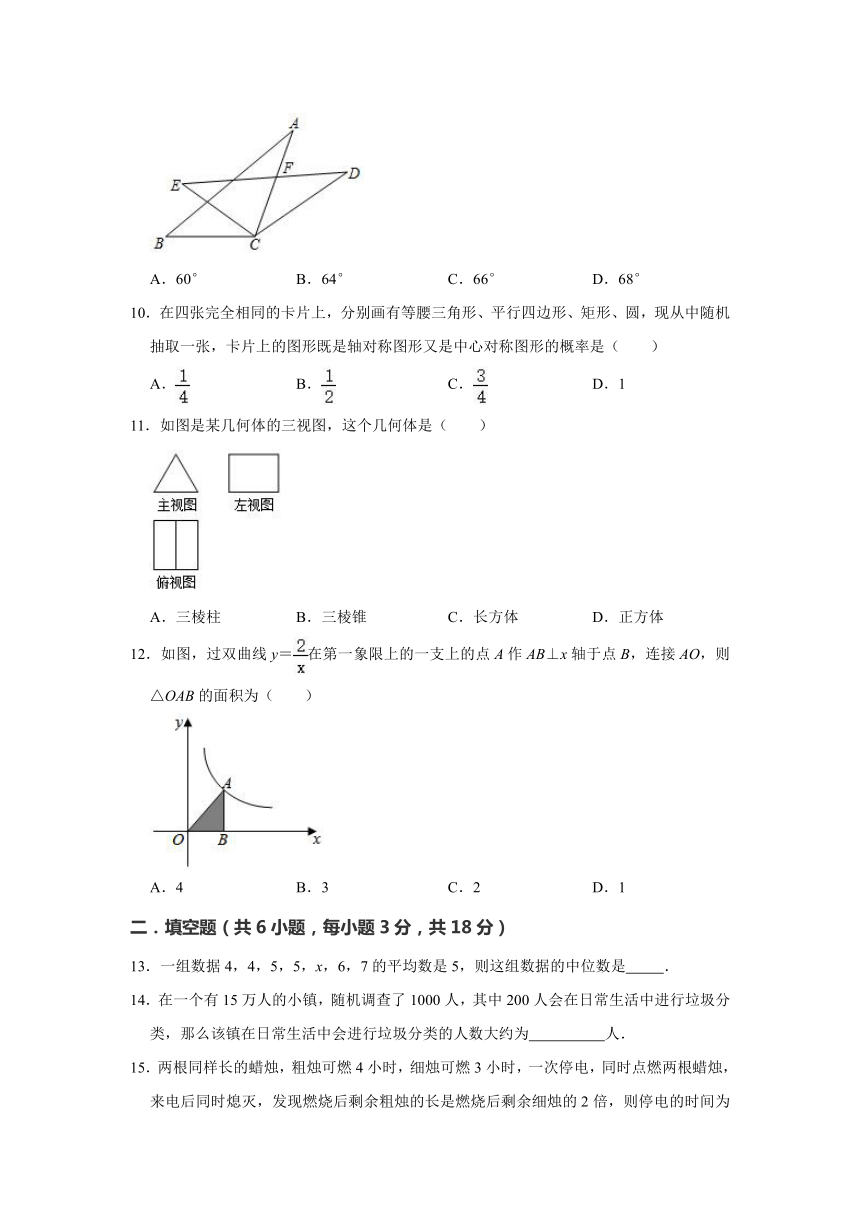
9.如图,在△ABC中,以C为中心,将△ABC顺时针旋转34°得到△DEC,边ED,AC相交于点F,若∠A=30°,则∠EFC的度数为( )
A.60°
B.64°
C.66°
D.68°
10.在四张完全相同的卡片上,分别画有等腰三角形、平行四边形、矩形、圆,现从中随机抽取一张,卡片上的图形既是轴对称图形又是中心对称图形的概率是( )
A.
B.
C.
D.1
11.如图是某几何体的三视图,这个几何体是( )
A.三棱柱
B.三棱锥
C.长方体
D.正方体
12.如图,过双曲线y=在第一象限上的一支上的点A作AB⊥x轴于点B,连接AO,则△OAB的面积为( )
A.4
B.3
C.2
D.1
二.填空题(共6小题,每小题3分,共18分)
13.一组数据4,4,5,5,x,6,7的平均数是5,则这组数据的中位数是
.
14.在一个有15万人的小镇,随机调查了1000人,其中200人会在日常生活中进行垃圾分类,那么该镇在日常生活中会进行垃圾分类的人数大约为
人.
15.两根同样长的蜡烛,粗烛可燃4小时,细烛可燃3小时,一次停电,同时点燃两根蜡烛,来电后同时熄灭,发现燃烧后剩余粗烛的长是燃烧后剩余细烛的2倍,则停电的时间为
小时.
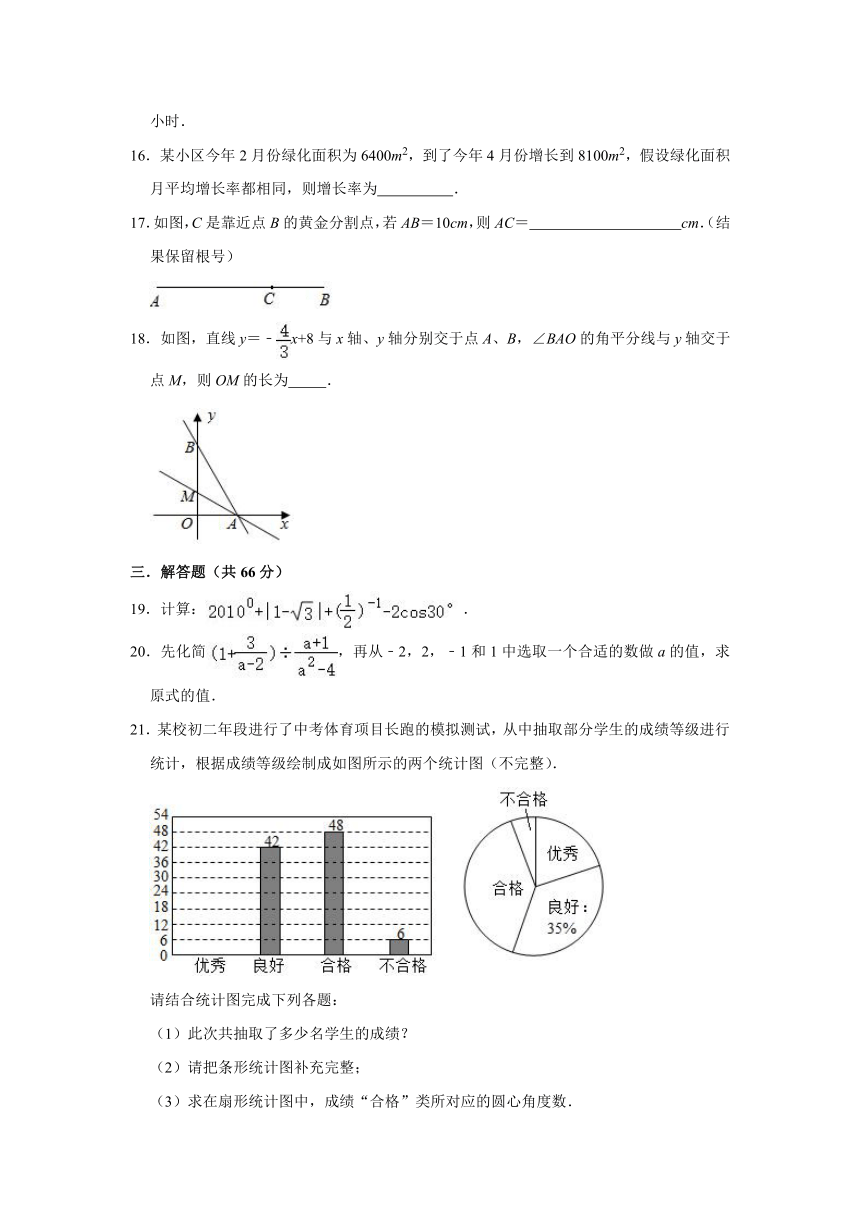
16.某小区今年2月份绿化面积为6400m2,到了今年4月份增长到8100m2,假设绿化面积月平均增长率都相同,则增长率为
.
17.如图,C是靠近点B的黄金分割点,若AB=10cm,则AC=
cm.(结果保留根号)
18.如图,直线y=﹣x+8与x轴、y轴分别交于点A、B,∠BAO的角平分线与y轴交于点M,则OM的长为
.
三.解答题(共66分)
19.计算:.
20.先化简,再从﹣2,2,﹣1和1中选取一个合适的数做a的值,求原式的值.
21.某校初二年段进行了中考体育项目长跑的模拟测试,从中抽取部分学生的成绩等级进行统计,根据成绩等级绘制成如图所示的两个统计图(不完整).
请结合统计图完成下列各题:
(1)此次共抽取了多少名学生的成绩?
(2)请把条形统计图补充完整;
(3)求在扇形统计图中,成绩“合格”类所对应的圆心角度数.
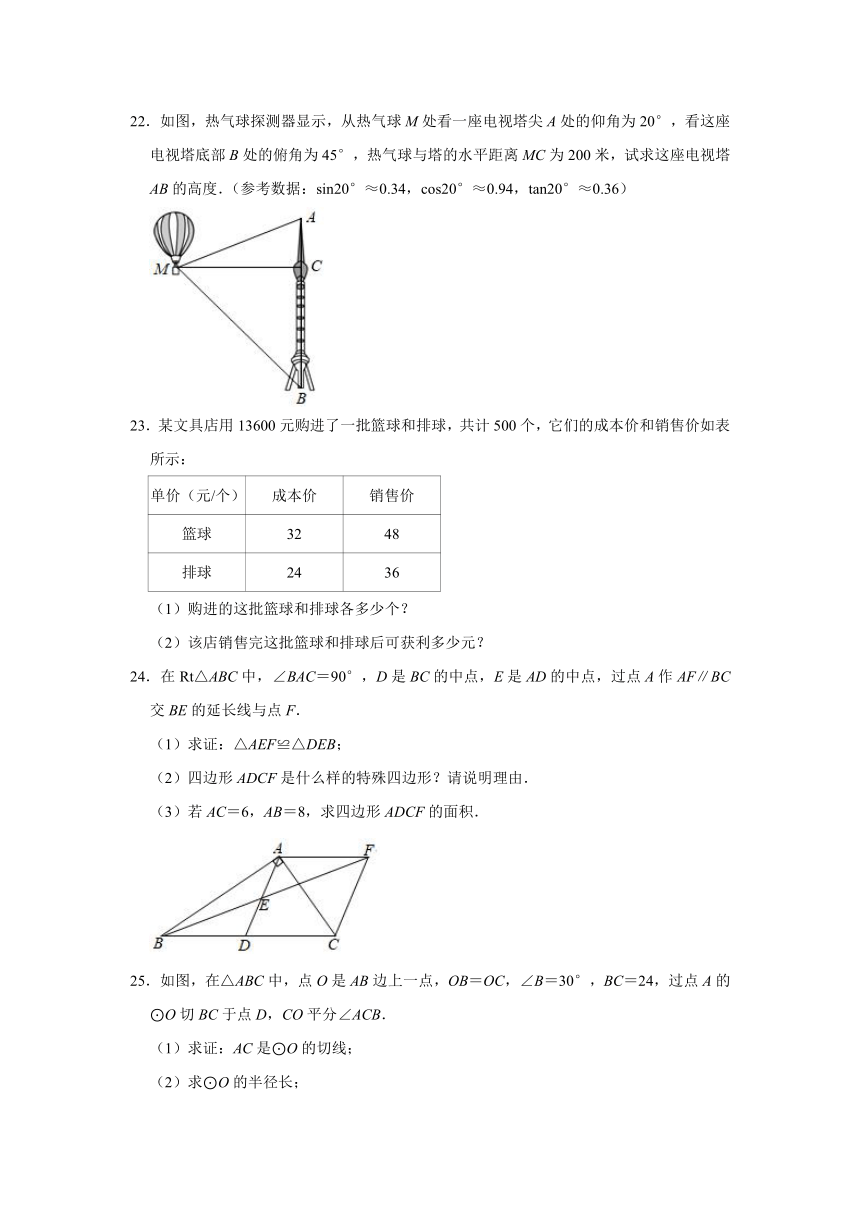
22.如图,热气球探测器显示,从热气球M处看一座电视塔尖A处的仰角为20°,看这座电视塔底部B处的俯角为45°,热气球与塔的水平距离MC为200米,试求这座电视塔AB的高度.(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
23.某文具店用13600元购进了一批篮球和排球,共计500个,它们的成本价和销售价如表所示:
单价(元/个)
成本价
销售价
篮球
32
48
排球
24
36
(1)购进的这批篮球和排球各多少个?
(2)该店销售完这批篮球和排球后可获利多少元?
24.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线与点F.
(1)求证:△AEF≌△DEB;
(2)四边形ADCF是什么样的特殊四边形?请说明理由.
(3)若AC=6,AB=8,求四边形ADCF的面积.
25.如图,在△ABC中,点O是AB边上一点,OB=OC,∠B=30°,BC=24,过点A的⊙O切BC于点D,CO平分∠ACB.
(1)求证:AC是⊙O的切线;
(2)求⊙O的半径长;
(3)求阴影部分的面积.
26.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图的顶点为点D,与y轴交于点C,与x轴交于A(﹣1,0),B(3,0)两点.
(1)求这个二次函数的解析式;
(2)若点P是x轴上一动点,当△PCD的周长最小时,求点P的坐标;
(3)如图,若点G(2,m)是该抛物线上一点,E是直线AG下方抛物线上的一动点,点E到直线AG的距离为d,求d的最大值.
2020-2021学年湖南省娄底涟源市九年级(下)第一次月考数学试卷
参考答案与试题解析
一.选择题(共12小题)
1.嫦娥五号从月球风驰电掣般返回地球的速度接近第二宇宙速度,即112000米/秒,数字112000用科学记数法表示为( )
A.112×103
B.1.12×103
C.1.12×105
D.1.12×106
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于10时,n是正数;当原数的绝对值小于1时,n是负数.
【解答】解:112000=1.12×105,
故选:C.
2.若代数式有意义,则实数x的取值范围是( )
A.x>0
B.x≥0
C.x>0且x≠2
D.x≥0且x≠2
【分析】根据分式、二次根式有意义的条件即可求出答案.
【解答】解:由题意可知:
,
∴x≥0且x≠2,
故选:D.
3.已知﹣5xay与2x2yb为同类项,则a﹣b的值为( )
A.1
B.2
C.3
D.4
【分析】根据同类项:所含字母相同,并且相同字母的指数也相同,可得出a、b的值,代入运算即可.
【解答】解:∵﹣5xay与2x2yb是同类项,
∴a=2,b=1,
故a﹣b=2﹣1=1.
故选:A.
4.多项式8a3b2+12a3bc﹣4a2b中,各项的公因式是( )
A.a2b
B.﹣4a2b2
C.4a2b
D.﹣a2b
【分析】利用公因式的确定方法可得答案.
【解答】解:多项式8a3b2+12a3bc﹣4a2b中各项的公因式是4a2b,
故选:C.
5.不等式组的解集是( )
A.﹣1<x≤2
B.﹣2≤x<1
C.x<﹣1或x≥2
D.2≤x<﹣1
【分析】分别求出各不等式的解集,再求出其公共解集.
【解答】解:,
由①得,x≤2,
由②得,x>﹣1,
故此不等式组的解集为:﹣1<x≤2.
故选:A.
6.在海上,灯塔位于一艘船的北偏东40度方向,那么这艘船位于这个灯塔的( )
A.南偏西40度方向
B.南偏西50度方向
C.北偏东50度方向
D.北偏东40度方向
【分析】方向角一般是指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标的方向线所成的角(一般指锐角),通常表达成北(南)偏东(西)××度.根据定义就可以解决.
【解答】解:灯塔位于一艘船的北偏东40度方向,那么这艘船位于这个灯塔的南偏西40度的方向.
故选:A.
7.设等腰三角形的一边长为5,另一边长为10,则其周长为( )
A.15
B.20
C.25
D.20或25
【分析】题目给出等腰三角形有两条边长为5和10,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
【解答】解:分两种情况:
当腰为5时,5+5=10,所以不能构成三角形;
当腰为10时,5+10>10,所以能构成三角形,周长是:10+10+5=25.
故选:C.
8.在平面直角坐标系内,将点A(1,2)先向右平移2个单位长度,再向下平移1个单位长度,则平移后所得点的坐标是( )
A.(3,1)
B.(3,3)
C.(﹣1,1)
D.(﹣1,3)
【分析】根据平移的法则即可得出平移后所得点的坐标.
【解答】解:将点A(1,2)先向右平移2个单位长度,再向下平移1个单位长度,则平移后所得点的坐标是(1+2,2﹣1),
即(3,1),
故选:A.
9.如图,在△ABC中,以C为中心,将△ABC顺时针旋转34°得到△DEC,边ED,AC相交于点F,若∠A=30°,则∠EFC的度数为( )
A.60°
B.64°
C.66°
D.68°
【分析】由旋转的性质得出∠D=∠A=30°,∠DCF=34°,由三角形的外角性质即可得出答案.
【解答】解:由旋转的性质得:∠D=∠A=30°,∠DCF=34°,
∴∠EFC=∠A+∠DCF=30°+34°=64°;
故选:B.
10.在四张完全相同的卡片上,分别画有等腰三角形、平行四边形、矩形、圆,现从中随机抽取一张,卡片上的图形既是轴对称图形又是中心对称图形的概率是( )
A.
B.
C.
D.1
【分析】由四张完全相同的卡片上分别画有等腰三角形、平行四边形、矩形、圆,其中既是轴对称图形又是中心对称图形的有矩形、圆,再根据概率公式求解即可.
【解答】解:∵四张完全相同的卡片上分别画有等腰三角形、平行四边形、矩形、圆,其中既是轴对称图形又是中心对称图形的有矩形、圆,
∴现从中任意抽取一张,卡片上所画的图形既是轴对称图形又是中心对称图形的概率为=,
故选:B.
11.如图是某几何体的三视图,这个几何体是( )
A.三棱柱
B.三棱锥
C.长方体
D.正方体
【分析】由俯视图和左视图确定是柱体,锥体还是球体,再由主视图确定具体形状.
【解答】解:根据俯视图和左视图为矩形判断出是柱体,根据主视图是三角形可判断出这个几何体应该是三棱柱,
故选:A.
12.如图,过双曲线y=在第一象限上的一支上的点A作AB⊥x轴于点B,连接AO,则△OAB的面积为( )
A.4
B.3
C.2
D.1
【分析】利用反比例函数系数k的几何意义即可得出△OAB的面积,即可得出答案.
【解答】解:∵过双曲线y=在第一象限上的一支上的点A作AB⊥x轴于点B,
∴S△AOB=|k|=×2=1,
故选:D.
二.填空题(共6小题)
13.一组数据4,4,5,5,x,6,7的平均数是5,则这组数据的中位数是 5 .
【分析】根据算术平均数、中位数的概念,结合题意进行求解.
【解答】解:∵这组数据的平均数是5,
∴=5,
解得:x=4,
这组数据按照从小到大的顺序排列为:4,4,4,5,5,6,7,
则中位数为5,
故答案为5.
14.在一个有15万人的小镇,随机调查了1000人,其中200人会在日常生活中进行垃圾分类,那么该镇在日常生活中会进行垃圾分类的人数大约为 30000 人.
【分析】先求出样本中会进行垃圾分类的人数所占的百分比,再乘以小镇的总人数即可.
【解答】解:由题意可得,该镇在日常生活中会进行垃圾分类的人数大约为:
150000×=30000(人).
故答案为:30000.
15.两根同样长的蜡烛,粗烛可燃4小时,细烛可燃3小时,一次停电,同时点燃两根蜡烛,来电后同时熄灭,发现燃烧后剩余粗烛的长是燃烧后剩余细烛的2倍,则停电的时间为 小时.
【分析】设停电的时间为x小时,根据“来电后同时熄灭,发现燃烧后剩余粗烛的长是燃烧后剩余细烛的2倍”,即可得出关于x的一元一次方程,解之即可得出结论.
【解答】解:设停电的时间为x小时,
依题意得:1﹣=2×(1﹣),
解得:x=.
故答案为:.
16.某小区今年2月份绿化面积为6400m2,到了今年4月份增长到8100m2,假设绿化面积月平均增长率都相同,则增长率为 12.5% .
【分析】设增长率为x,根据题意列出方程,求出方程的解即可得到结果.
【解答】解:设增长率为x,
根据题意得:6400(1+x)2=8100,即(1+x)2=,
开方得:1+x=±,
解得:x1==12.5%,x2=﹣(舍去),
则增长率为12.5%.
故答案为:12.5%.
17.如图,C是靠近点B的黄金分割点,若AB=10cm,则AC= (5﹣5) cm.(结果保留根号)
【分析】直接由黄金分割点的定义和黄金比值代入计算即可.
【解答】解:∵C是靠近点B的黄金分割点,AB=10cm,
∴AC>BC,AC=AB=×10=(5﹣5)cm,
故答案为:(5﹣5).
18.如图,直线y=﹣x+8与x轴、y轴分别交于点A、B,∠BAO的角平分线与y轴交于点M,则OM的长为 3 .
【分析】过M点作MN⊥AB于N,如图,先利用坐标轴上点的坐标特征求出A、B点的坐标,则可计算出AB=10,再利用角平分线的性质得MO=MN,然后利用面积法得到×6?OM+×10?MN=×6×8,从而可求出OM的长.
【解答】解:过M点作MN⊥AB于N,如图,
当y=0时,﹣x+8=0,解得x=6,则A(6,0);
当x=0时,y=﹣x+8=8,则B(0,8),
∴AB==10,
∵AM平分∠OAB,
∴MO=MN,
∵S△OMA+S△BMA=S△OAB,
∴×6?OM+×10?MN=×6×8,
即3OM+5MN=24,
∴8OM=24,
∴OM=3.
故答案为3.
三.解答题
19.计算:.
【分析】直接利用零指数幂的性质、负整数指数幂的性质以及绝对值的性质分别化简得出答案.
【解答】解:原式=1+﹣1+2﹣2×
=1+﹣1+2﹣
=2.
20.先化简,再从﹣2,2,﹣1和1中选取一个合适的数做a的值,求原式的值.
【分析】根据分式的混合运算法则把原式化简,根据分式有意义的条件确定a的值,代入计算即可.
【解答】解:原式=(+)÷
=×
=a+2,
由题意得,a2﹣4≠0,a+1≠0,
则a≠±2,a≠﹣1,
∴a=1,
当a=1时,原式=1+2=3.
21.某校初二年段进行了中考体育项目长跑的模拟测试,从中抽取部分学生的成绩等级进行统计,根据成绩等级绘制成如图所示的两个统计图(不完整).
请结合统计图完成下列各题:
(1)此次共抽取了多少名学生的成绩?
(2)请把条形统计图补充完整;
(3)求在扇形统计图中,成绩“合格”类所对应的圆心角度数.
【分析】(1)根据成绩为良好的人数和所占的百分比可以求得本次共抽取了多少名学生的成绩;
(2)根据(1)中的结果和条形统计图中的数据,可以计算出成绩为优秀的人数,从而可以将条形统计图补充完整;
(3)根据统计图中的数据,可以计算出成绩“合格”类所对应的圆心角度数.
【解答】解:(1)42÷35%=120(名),
即此次共抽取了120名学生的成绩;
(2)成绩为优秀的学生有:120﹣42﹣48﹣6=24(人),
补全完整的条形统计图如右图所示;
(3)360°×=144°,
即在扇形统计图中,成绩“合格”类所对应的圆心角度数是144°.
22.如图,热气球探测器显示,从热气球M处看一座电视塔尖A处的仰角为20°,看这座电视塔底部B处的俯角为45°,热气球与塔的水平距离MC为200米,试求这座电视塔AB的高度.(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
【分析】根据仰角俯角定义,利用锐角三角函数即可求出结果.
【解答】解:根据题意可知:
∠ACM=∠BCM=90°,∠AMC=20°,∠BMC=45°,MC=200米,
在Rt△AMC中,
∵tan∠AMC=,
∴AC=72(米),
在Rt△BMC中,
∵∠BCM=90°,∠BMC=45°,
∴BC=MC=200(米),
∴AB=AC+BC=72+200=272(米).
答:这座电视塔AB的高度为272米.
23.某文具店用13600元购进了一批篮球和排球,共计500个,它们的成本价和销售价如表所示:
单价(元/个)
成本价
销售价
篮球
32
48
排球
24
36
(1)购进的这批篮球和排球各多少个?
(2)该店销售完这批篮球和排球后可获利多少元?
【分析】(1)设购进篮球x个,排球y个,根据购进的两种球共500个且共花费了13600元,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)利用总利润=每个球的销售利润×销售数量,即可求出结论.
【解答】解:(1)设购进篮球x个,排球y个,
依题意得:,
解得:.
答:购进篮球200个,排球300个.
(2)(48﹣32)×200+(36﹣24)×300=6800(元).
答:该店销售完这批篮球和排球后可获利6800元.
24.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线与点F.
(1)求证:△AEF≌△DEB;
(2)四边形ADCF是什么样的特殊四边形?请说明理由.
(3)若AC=6,AB=8,求四边形ADCF的面积.
【分析】(1)由AAS证明△AEF≌△DEB即可.
(2)由全等三角形的性质得AF=DB,证得四边形ADCF为平行四边形,再利用直角三角形的性质可求得AD=CD,可证得结论;
(3)根据条件可证得S菱形ADCF=S△ABC,由三角形面积公式可求得答案.
【解答】(1)证明:∵E是AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,
在△AEF和△DEB中,
,
∴△AEF≌△DEB(AAS).
(2)结论:四边形ADCF是菱形.
理由:由(1)得:△AEF≌△DEB,
∴AF=DB,
又∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=BC=CD,
∴四边形ADCF是菱形.
(3)解:∵D是BC的中点,
∴S菱形ADCF=2S△ADC=S△ABC=AB?AC=×8×6=24.
25.如图,在△ABC中,点O是AB边上一点,OB=OC,∠B=30°,BC=24,过点A的⊙O切BC于点D,CO平分∠ACB.
(1)求证:AC是⊙O的切线;
(2)求⊙O的半径长;
(3)求阴影部分的面积.
【分析】(1)由等腰三角形的性质得出∠OCB=∠B=30°,由角平分线的定义以及切线的判定定理即可得出结论;
(2)连接OD,设OC交⊙O于点F,得出∠COD=∠BOD=60°,CD=BC=6,解直角三角形即可得出结果;
(3)由三角形的面积公式和扇形的面积公式可得出答案.
【解答】(1)证明:∵OB=OC,∠B=30°,
∴∠OCB=∠B=30°,
又∵CO平分∠ACB,
∴∠ACB=2∠OCB=60°,
∴∠BAC=180°﹣∠ACB﹣∠B=180°﹣60°﹣30°=90°,
∴OA⊥AC,
∴AC是⊙O的切线;
(2)解:连接OD,设OC交⊙O于点F,如图所示:
∵⊙O切BC于点D,
∴OD⊥BC,
又∵OB=OC,∠B=30°,BC=24,
∴∠COD=∠BOD=60°,CD=BC=12,
∵tan∠COD=,
∴OD====4;
(3)解:∵OD=4,∠DOF=60°,
∴S阴影=S△OCD﹣S扇形ODF=×12×4﹣=24﹣8π.
26.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图的顶点为点D,与y轴交于点C,与x轴交于A(﹣1,0),B(3,0)两点.
(1)求这个二次函数的解析式;
(2)若点P是x轴上一动点,当△PCD的周长最小时,求点P的坐标;
(3)如图,若点G(2,m)是该抛物线上一点,E是直线AG下方抛物线上的一动点,点E到直线AG的距离为d,求d的最大值.
【分析】(1)由二次函数y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,求得其对称轴,从而可得b的值,再将(﹣1,0)代入即可求得c的值,则可得抛物线的解析式;
(2)作点C关于x轴的对称点F,则F的坐标为(0,3),连接DF交x轴于顶点P,此时△PCD的周长最小,用待定系数法求得直线DF的解析式,令y=0,可得点P的横坐标,则问题得解;
(3)先求得点G的坐标,再用待定系数法求得直线AG的解析式;作AG的平行线MN,交x轴于点M,交y轴于点N,过点A作AH⊥MN于点H当直线MN与抛物线相切时,点E到直线AG的距离d=EK最大,设直线MN的解析式为y=﹣x+n,将其与抛物线解析式联立,得出关于x的一元二次方程,由交点个数与方程的判别式的关系可得△=0,从而可得n的值,最后由三角函数求得AH的值,即为所求的d的最大值.
【解答】解:(1)∵二次函数y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,
∴对称轴为x=1,
∴﹣=1,
∴b=﹣2,
∴y=x2﹣2x+c,
将(﹣1,0)代入得:
0=1+2+c,
∴c=﹣3,
∴这个二次函数的解析式为y=x2﹣2x﹣3;
(2)∵抛物线y=x2﹣2x﹣3的对称轴为x=1,
∴顶点D的坐标为(1,﹣4),点C的坐标为(0,﹣3).
作点C关于x轴的对称点F,则F的坐标为(0,3),连接DF交x轴于顶点P,此时△PCD的周长最小,如图:
设直线DF的解析式为y=kx+b(k≠0),将D(1,﹣4),F(0,3)分别代入得:
,
∴y=﹣7x+3,
当y=0时,x=,
∴点P的坐标为(,0);
(3)∵抛物线y=x2﹣2x﹣3,点G(2,m)是该抛物线上一点,
∴m=22﹣2×2﹣3=﹣3,
∴点G(2,﹣3),
设直线AG的解析式为:y=px+q(p≠0),
将A(﹣1,0),G(2,﹣3)分别代入得:
,
解得,
∴直线AG的解析式为:y=﹣x﹣1,
作AG的平行线MN,交x轴于点M,交y轴于点N,过点A作AH⊥MN于点H,如图:
当直线MN与抛物线相切时,点E到直线AG的距离d=EK最大,
∵AG∥MN,
∴AH=EK=d.
设直线MN的解析式为y=﹣x+n,将其与抛物线解析式联立得:
,
∴x2﹣2x﹣3=﹣x+n,
整理得:x2﹣x﹣3﹣n=0,
当MN与抛物线相切时,△=0,
∴(﹣1)2﹣4(﹣3﹣n)=0,
解得:n=﹣,
∴直线MN的解析式为y=﹣x﹣,
∴点M的坐标为(﹣,0),点N坐标为(0,﹣),
∴AM=﹣1﹣(﹣)=,
∵OM=ON=,
∴∠AMN=45°,
∴AH=AM?sin45°
=×
=,
∴d的最大值为.
一.选择题(共12小题,每小题3分,共36分)
1.嫦娥五号从月球风驰电掣般返回地球的速度接近第二宇宙速度,即112000米/秒,数字112000用科学记数法表示为( )
A.112×103
B.1.12×103
C.1.12×105
D.1.12×106
2.若代数式有意义,则实数x的取值范围是( )
A.x>0
B.x≥0
C.x>0且x≠2
D.x≥0且x≠2
3.已知﹣5xay与2x2yb为同类项,则a﹣b的值为( )
A.1
B.2
C.3
D.4
4.多项式8a3b2+12a3bc﹣4a2b中,各项的公因式是( )
A.a2b
B.﹣4a2b2
C.4a2b
D.﹣a2b
5.不等式组的解集是( )
A.﹣1<x≤2
B.﹣2≤x<1
C.x<﹣1或x≥2
D.2≤x<﹣1
6.在海上,灯塔位于一艘船的北偏东40度方向,那么这艘船位于这个灯塔的( )
A.南偏西40度方向
B.南偏西50度方向
C.北偏东50度方向
D.北偏东40度方向
7.设等腰三角形的一边长为5,另一边长为10,则其周长为( )
A.15
B.20
C.25
D.20或25
8.在平面直角坐标系内,将点A(1,2)先向右平移2个单位长度,再向下平移1个单位长度,则平移后所得点的坐标是( )
A.(3,1)
B.(3,3)
C.(﹣1,1)
D.(﹣1,3)
9.如图,在△ABC中,以C为中心,将△ABC顺时针旋转34°得到△DEC,边ED,AC相交于点F,若∠A=30°,则∠EFC的度数为( )
A.60°
B.64°
C.66°
D.68°
10.在四张完全相同的卡片上,分别画有等腰三角形、平行四边形、矩形、圆,现从中随机抽取一张,卡片上的图形既是轴对称图形又是中心对称图形的概率是( )
A.
B.
C.
D.1
11.如图是某几何体的三视图,这个几何体是( )
A.三棱柱
B.三棱锥
C.长方体
D.正方体
12.如图,过双曲线y=在第一象限上的一支上的点A作AB⊥x轴于点B,连接AO,则△OAB的面积为( )
A.4
B.3
C.2
D.1
二.填空题(共6小题,每小题3分,共18分)
13.一组数据4,4,5,5,x,6,7的平均数是5,则这组数据的中位数是
.
14.在一个有15万人的小镇,随机调查了1000人,其中200人会在日常生活中进行垃圾分类,那么该镇在日常生活中会进行垃圾分类的人数大约为
人.
15.两根同样长的蜡烛,粗烛可燃4小时,细烛可燃3小时,一次停电,同时点燃两根蜡烛,来电后同时熄灭,发现燃烧后剩余粗烛的长是燃烧后剩余细烛的2倍,则停电的时间为
小时.
16.某小区今年2月份绿化面积为6400m2,到了今年4月份增长到8100m2,假设绿化面积月平均增长率都相同,则增长率为
.
17.如图,C是靠近点B的黄金分割点,若AB=10cm,则AC=
cm.(结果保留根号)
18.如图,直线y=﹣x+8与x轴、y轴分别交于点A、B,∠BAO的角平分线与y轴交于点M,则OM的长为
.
三.解答题(共66分)
19.计算:.
20.先化简,再从﹣2,2,﹣1和1中选取一个合适的数做a的值,求原式的值.
21.某校初二年段进行了中考体育项目长跑的模拟测试,从中抽取部分学生的成绩等级进行统计,根据成绩等级绘制成如图所示的两个统计图(不完整).
请结合统计图完成下列各题:
(1)此次共抽取了多少名学生的成绩?
(2)请把条形统计图补充完整;
(3)求在扇形统计图中,成绩“合格”类所对应的圆心角度数.
22.如图,热气球探测器显示,从热气球M处看一座电视塔尖A处的仰角为20°,看这座电视塔底部B处的俯角为45°,热气球与塔的水平距离MC为200米,试求这座电视塔AB的高度.(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
23.某文具店用13600元购进了一批篮球和排球,共计500个,它们的成本价和销售价如表所示:
单价(元/个)
成本价
销售价
篮球
32
48
排球
24
36
(1)购进的这批篮球和排球各多少个?
(2)该店销售完这批篮球和排球后可获利多少元?
24.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线与点F.
(1)求证:△AEF≌△DEB;
(2)四边形ADCF是什么样的特殊四边形?请说明理由.
(3)若AC=6,AB=8,求四边形ADCF的面积.
25.如图,在△ABC中,点O是AB边上一点,OB=OC,∠B=30°,BC=24,过点A的⊙O切BC于点D,CO平分∠ACB.
(1)求证:AC是⊙O的切线;
(2)求⊙O的半径长;
(3)求阴影部分的面积.
26.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图的顶点为点D,与y轴交于点C,与x轴交于A(﹣1,0),B(3,0)两点.
(1)求这个二次函数的解析式;
(2)若点P是x轴上一动点,当△PCD的周长最小时,求点P的坐标;
(3)如图,若点G(2,m)是该抛物线上一点,E是直线AG下方抛物线上的一动点,点E到直线AG的距离为d,求d的最大值.
2020-2021学年湖南省娄底涟源市九年级(下)第一次月考数学试卷
参考答案与试题解析
一.选择题(共12小题)
1.嫦娥五号从月球风驰电掣般返回地球的速度接近第二宇宙速度,即112000米/秒,数字112000用科学记数法表示为( )
A.112×103
B.1.12×103
C.1.12×105
D.1.12×106
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于10时,n是正数;当原数的绝对值小于1时,n是负数.
【解答】解:112000=1.12×105,
故选:C.
2.若代数式有意义,则实数x的取值范围是( )
A.x>0
B.x≥0
C.x>0且x≠2
D.x≥0且x≠2
【分析】根据分式、二次根式有意义的条件即可求出答案.
【解答】解:由题意可知:
,
∴x≥0且x≠2,
故选:D.
3.已知﹣5xay与2x2yb为同类项,则a﹣b的值为( )
A.1
B.2
C.3
D.4
【分析】根据同类项:所含字母相同,并且相同字母的指数也相同,可得出a、b的值,代入运算即可.
【解答】解:∵﹣5xay与2x2yb是同类项,
∴a=2,b=1,
故a﹣b=2﹣1=1.
故选:A.
4.多项式8a3b2+12a3bc﹣4a2b中,各项的公因式是( )
A.a2b
B.﹣4a2b2
C.4a2b
D.﹣a2b
【分析】利用公因式的确定方法可得答案.
【解答】解:多项式8a3b2+12a3bc﹣4a2b中各项的公因式是4a2b,
故选:C.
5.不等式组的解集是( )
A.﹣1<x≤2
B.﹣2≤x<1
C.x<﹣1或x≥2
D.2≤x<﹣1
【分析】分别求出各不等式的解集,再求出其公共解集.
【解答】解:,
由①得,x≤2,
由②得,x>﹣1,
故此不等式组的解集为:﹣1<x≤2.
故选:A.
6.在海上,灯塔位于一艘船的北偏东40度方向,那么这艘船位于这个灯塔的( )
A.南偏西40度方向
B.南偏西50度方向
C.北偏东50度方向
D.北偏东40度方向
【分析】方向角一般是指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标的方向线所成的角(一般指锐角),通常表达成北(南)偏东(西)××度.根据定义就可以解决.
【解答】解:灯塔位于一艘船的北偏东40度方向,那么这艘船位于这个灯塔的南偏西40度的方向.
故选:A.
7.设等腰三角形的一边长为5,另一边长为10,则其周长为( )
A.15
B.20
C.25
D.20或25
【分析】题目给出等腰三角形有两条边长为5和10,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
【解答】解:分两种情况:
当腰为5时,5+5=10,所以不能构成三角形;
当腰为10时,5+10>10,所以能构成三角形,周长是:10+10+5=25.
故选:C.
8.在平面直角坐标系内,将点A(1,2)先向右平移2个单位长度,再向下平移1个单位长度,则平移后所得点的坐标是( )
A.(3,1)
B.(3,3)
C.(﹣1,1)
D.(﹣1,3)
【分析】根据平移的法则即可得出平移后所得点的坐标.
【解答】解:将点A(1,2)先向右平移2个单位长度,再向下平移1个单位长度,则平移后所得点的坐标是(1+2,2﹣1),
即(3,1),
故选:A.
9.如图,在△ABC中,以C为中心,将△ABC顺时针旋转34°得到△DEC,边ED,AC相交于点F,若∠A=30°,则∠EFC的度数为( )
A.60°
B.64°
C.66°
D.68°
【分析】由旋转的性质得出∠D=∠A=30°,∠DCF=34°,由三角形的外角性质即可得出答案.
【解答】解:由旋转的性质得:∠D=∠A=30°,∠DCF=34°,
∴∠EFC=∠A+∠DCF=30°+34°=64°;
故选:B.
10.在四张完全相同的卡片上,分别画有等腰三角形、平行四边形、矩形、圆,现从中随机抽取一张,卡片上的图形既是轴对称图形又是中心对称图形的概率是( )
A.
B.
C.
D.1
【分析】由四张完全相同的卡片上分别画有等腰三角形、平行四边形、矩形、圆,其中既是轴对称图形又是中心对称图形的有矩形、圆,再根据概率公式求解即可.
【解答】解:∵四张完全相同的卡片上分别画有等腰三角形、平行四边形、矩形、圆,其中既是轴对称图形又是中心对称图形的有矩形、圆,
∴现从中任意抽取一张,卡片上所画的图形既是轴对称图形又是中心对称图形的概率为=,
故选:B.
11.如图是某几何体的三视图,这个几何体是( )
A.三棱柱
B.三棱锥
C.长方体
D.正方体
【分析】由俯视图和左视图确定是柱体,锥体还是球体,再由主视图确定具体形状.
【解答】解:根据俯视图和左视图为矩形判断出是柱体,根据主视图是三角形可判断出这个几何体应该是三棱柱,
故选:A.
12.如图,过双曲线y=在第一象限上的一支上的点A作AB⊥x轴于点B,连接AO,则△OAB的面积为( )
A.4
B.3
C.2
D.1
【分析】利用反比例函数系数k的几何意义即可得出△OAB的面积,即可得出答案.
【解答】解:∵过双曲线y=在第一象限上的一支上的点A作AB⊥x轴于点B,
∴S△AOB=|k|=×2=1,
故选:D.
二.填空题(共6小题)
13.一组数据4,4,5,5,x,6,7的平均数是5,则这组数据的中位数是 5 .
【分析】根据算术平均数、中位数的概念,结合题意进行求解.
【解答】解:∵这组数据的平均数是5,
∴=5,
解得:x=4,
这组数据按照从小到大的顺序排列为:4,4,4,5,5,6,7,
则中位数为5,
故答案为5.
14.在一个有15万人的小镇,随机调查了1000人,其中200人会在日常生活中进行垃圾分类,那么该镇在日常生活中会进行垃圾分类的人数大约为 30000 人.
【分析】先求出样本中会进行垃圾分类的人数所占的百分比,再乘以小镇的总人数即可.
【解答】解:由题意可得,该镇在日常生活中会进行垃圾分类的人数大约为:
150000×=30000(人).
故答案为:30000.
15.两根同样长的蜡烛,粗烛可燃4小时,细烛可燃3小时,一次停电,同时点燃两根蜡烛,来电后同时熄灭,发现燃烧后剩余粗烛的长是燃烧后剩余细烛的2倍,则停电的时间为 小时.
【分析】设停电的时间为x小时,根据“来电后同时熄灭,发现燃烧后剩余粗烛的长是燃烧后剩余细烛的2倍”,即可得出关于x的一元一次方程,解之即可得出结论.
【解答】解:设停电的时间为x小时,
依题意得:1﹣=2×(1﹣),
解得:x=.
故答案为:.
16.某小区今年2月份绿化面积为6400m2,到了今年4月份增长到8100m2,假设绿化面积月平均增长率都相同,则增长率为 12.5% .
【分析】设增长率为x,根据题意列出方程,求出方程的解即可得到结果.
【解答】解:设增长率为x,
根据题意得:6400(1+x)2=8100,即(1+x)2=,
开方得:1+x=±,
解得:x1==12.5%,x2=﹣(舍去),
则增长率为12.5%.
故答案为:12.5%.
17.如图,C是靠近点B的黄金分割点,若AB=10cm,则AC= (5﹣5) cm.(结果保留根号)
【分析】直接由黄金分割点的定义和黄金比值代入计算即可.
【解答】解:∵C是靠近点B的黄金分割点,AB=10cm,
∴AC>BC,AC=AB=×10=(5﹣5)cm,
故答案为:(5﹣5).
18.如图,直线y=﹣x+8与x轴、y轴分别交于点A、B,∠BAO的角平分线与y轴交于点M,则OM的长为 3 .
【分析】过M点作MN⊥AB于N,如图,先利用坐标轴上点的坐标特征求出A、B点的坐标,则可计算出AB=10,再利用角平分线的性质得MO=MN,然后利用面积法得到×6?OM+×10?MN=×6×8,从而可求出OM的长.
【解答】解:过M点作MN⊥AB于N,如图,
当y=0时,﹣x+8=0,解得x=6,则A(6,0);
当x=0时,y=﹣x+8=8,则B(0,8),
∴AB==10,
∵AM平分∠OAB,
∴MO=MN,
∵S△OMA+S△BMA=S△OAB,
∴×6?OM+×10?MN=×6×8,
即3OM+5MN=24,
∴8OM=24,
∴OM=3.
故答案为3.
三.解答题
19.计算:.
【分析】直接利用零指数幂的性质、负整数指数幂的性质以及绝对值的性质分别化简得出答案.
【解答】解:原式=1+﹣1+2﹣2×
=1+﹣1+2﹣
=2.
20.先化简,再从﹣2,2,﹣1和1中选取一个合适的数做a的值,求原式的值.
【分析】根据分式的混合运算法则把原式化简,根据分式有意义的条件确定a的值,代入计算即可.
【解答】解:原式=(+)÷
=×
=a+2,
由题意得,a2﹣4≠0,a+1≠0,
则a≠±2,a≠﹣1,
∴a=1,
当a=1时,原式=1+2=3.
21.某校初二年段进行了中考体育项目长跑的模拟测试,从中抽取部分学生的成绩等级进行统计,根据成绩等级绘制成如图所示的两个统计图(不完整).
请结合统计图完成下列各题:
(1)此次共抽取了多少名学生的成绩?
(2)请把条形统计图补充完整;
(3)求在扇形统计图中,成绩“合格”类所对应的圆心角度数.
【分析】(1)根据成绩为良好的人数和所占的百分比可以求得本次共抽取了多少名学生的成绩;
(2)根据(1)中的结果和条形统计图中的数据,可以计算出成绩为优秀的人数,从而可以将条形统计图补充完整;
(3)根据统计图中的数据,可以计算出成绩“合格”类所对应的圆心角度数.
【解答】解:(1)42÷35%=120(名),
即此次共抽取了120名学生的成绩;
(2)成绩为优秀的学生有:120﹣42﹣48﹣6=24(人),
补全完整的条形统计图如右图所示;
(3)360°×=144°,
即在扇形统计图中,成绩“合格”类所对应的圆心角度数是144°.
22.如图,热气球探测器显示,从热气球M处看一座电视塔尖A处的仰角为20°,看这座电视塔底部B处的俯角为45°,热气球与塔的水平距离MC为200米,试求这座电视塔AB的高度.(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
【分析】根据仰角俯角定义,利用锐角三角函数即可求出结果.
【解答】解:根据题意可知:
∠ACM=∠BCM=90°,∠AMC=20°,∠BMC=45°,MC=200米,
在Rt△AMC中,
∵tan∠AMC=,
∴AC=72(米),
在Rt△BMC中,
∵∠BCM=90°,∠BMC=45°,
∴BC=MC=200(米),
∴AB=AC+BC=72+200=272(米).
答:这座电视塔AB的高度为272米.
23.某文具店用13600元购进了一批篮球和排球,共计500个,它们的成本价和销售价如表所示:
单价(元/个)
成本价
销售价
篮球
32
48
排球
24
36
(1)购进的这批篮球和排球各多少个?
(2)该店销售完这批篮球和排球后可获利多少元?
【分析】(1)设购进篮球x个,排球y个,根据购进的两种球共500个且共花费了13600元,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)利用总利润=每个球的销售利润×销售数量,即可求出结论.
【解答】解:(1)设购进篮球x个,排球y个,
依题意得:,
解得:.
答:购进篮球200个,排球300个.
(2)(48﹣32)×200+(36﹣24)×300=6800(元).
答:该店销售完这批篮球和排球后可获利6800元.
24.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线与点F.
(1)求证:△AEF≌△DEB;
(2)四边形ADCF是什么样的特殊四边形?请说明理由.
(3)若AC=6,AB=8,求四边形ADCF的面积.
【分析】(1)由AAS证明△AEF≌△DEB即可.
(2)由全等三角形的性质得AF=DB,证得四边形ADCF为平行四边形,再利用直角三角形的性质可求得AD=CD,可证得结论;
(3)根据条件可证得S菱形ADCF=S△ABC,由三角形面积公式可求得答案.
【解答】(1)证明:∵E是AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,
在△AEF和△DEB中,
,
∴△AEF≌△DEB(AAS).
(2)结论:四边形ADCF是菱形.
理由:由(1)得:△AEF≌△DEB,
∴AF=DB,
又∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=BC=CD,
∴四边形ADCF是菱形.
(3)解:∵D是BC的中点,
∴S菱形ADCF=2S△ADC=S△ABC=AB?AC=×8×6=24.
25.如图,在△ABC中,点O是AB边上一点,OB=OC,∠B=30°,BC=24,过点A的⊙O切BC于点D,CO平分∠ACB.
(1)求证:AC是⊙O的切线;
(2)求⊙O的半径长;
(3)求阴影部分的面积.
【分析】(1)由等腰三角形的性质得出∠OCB=∠B=30°,由角平分线的定义以及切线的判定定理即可得出结论;
(2)连接OD,设OC交⊙O于点F,得出∠COD=∠BOD=60°,CD=BC=6,解直角三角形即可得出结果;
(3)由三角形的面积公式和扇形的面积公式可得出答案.
【解答】(1)证明:∵OB=OC,∠B=30°,
∴∠OCB=∠B=30°,
又∵CO平分∠ACB,
∴∠ACB=2∠OCB=60°,
∴∠BAC=180°﹣∠ACB﹣∠B=180°﹣60°﹣30°=90°,
∴OA⊥AC,
∴AC是⊙O的切线;
(2)解:连接OD,设OC交⊙O于点F,如图所示:
∵⊙O切BC于点D,
∴OD⊥BC,
又∵OB=OC,∠B=30°,BC=24,
∴∠COD=∠BOD=60°,CD=BC=12,
∵tan∠COD=,
∴OD====4;
(3)解:∵OD=4,∠DOF=60°,
∴S阴影=S△OCD﹣S扇形ODF=×12×4﹣=24﹣8π.
26.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图的顶点为点D,与y轴交于点C,与x轴交于A(﹣1,0),B(3,0)两点.
(1)求这个二次函数的解析式;
(2)若点P是x轴上一动点,当△PCD的周长最小时,求点P的坐标;
(3)如图,若点G(2,m)是该抛物线上一点,E是直线AG下方抛物线上的一动点,点E到直线AG的距离为d,求d的最大值.
【分析】(1)由二次函数y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,求得其对称轴,从而可得b的值,再将(﹣1,0)代入即可求得c的值,则可得抛物线的解析式;
(2)作点C关于x轴的对称点F,则F的坐标为(0,3),连接DF交x轴于顶点P,此时△PCD的周长最小,用待定系数法求得直线DF的解析式,令y=0,可得点P的横坐标,则问题得解;
(3)先求得点G的坐标,再用待定系数法求得直线AG的解析式;作AG的平行线MN,交x轴于点M,交y轴于点N,过点A作AH⊥MN于点H当直线MN与抛物线相切时,点E到直线AG的距离d=EK最大,设直线MN的解析式为y=﹣x+n,将其与抛物线解析式联立,得出关于x的一元二次方程,由交点个数与方程的判别式的关系可得△=0,从而可得n的值,最后由三角函数求得AH的值,即为所求的d的最大值.
【解答】解:(1)∵二次函数y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,
∴对称轴为x=1,
∴﹣=1,
∴b=﹣2,
∴y=x2﹣2x+c,
将(﹣1,0)代入得:
0=1+2+c,
∴c=﹣3,
∴这个二次函数的解析式为y=x2﹣2x﹣3;
(2)∵抛物线y=x2﹣2x﹣3的对称轴为x=1,
∴顶点D的坐标为(1,﹣4),点C的坐标为(0,﹣3).
作点C关于x轴的对称点F,则F的坐标为(0,3),连接DF交x轴于顶点P,此时△PCD的周长最小,如图:
设直线DF的解析式为y=kx+b(k≠0),将D(1,﹣4),F(0,3)分别代入得:
,
∴y=﹣7x+3,
当y=0时,x=,
∴点P的坐标为(,0);
(3)∵抛物线y=x2﹣2x﹣3,点G(2,m)是该抛物线上一点,
∴m=22﹣2×2﹣3=﹣3,
∴点G(2,﹣3),
设直线AG的解析式为:y=px+q(p≠0),
将A(﹣1,0),G(2,﹣3)分别代入得:
,
解得,
∴直线AG的解析式为:y=﹣x﹣1,
作AG的平行线MN,交x轴于点M,交y轴于点N,过点A作AH⊥MN于点H,如图:
当直线MN与抛物线相切时,点E到直线AG的距离d=EK最大,
∵AG∥MN,
∴AH=EK=d.
设直线MN的解析式为y=﹣x+n,将其与抛物线解析式联立得:
,
∴x2﹣2x﹣3=﹣x+n,
整理得:x2﹣x﹣3﹣n=0,
当MN与抛物线相切时,△=0,
∴(﹣1)2﹣4(﹣3﹣n)=0,
解得:n=﹣,
∴直线MN的解析式为y=﹣x﹣,
∴点M的坐标为(﹣,0),点N坐标为(0,﹣),
∴AM=﹣1﹣(﹣)=,
∵OM=ON=,
∴∠AMN=45°,
∴AH=AM?sin45°
=×
=,
∴d的最大值为.
同课章节目录
