2020-2021学年八年级数学沪科版下册 19.2 平行四边形的性质(共18张ppt)
文档属性
| 名称 | 2020-2021学年八年级数学沪科版下册 19.2 平行四边形的性质(共18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-05 16:57:01 | ||
图片预览





文档简介
(共18张PPT)
平行四边形的性质
活动一
你能用你手中一对全等的三角形纸片拼出什么样的几何图形?
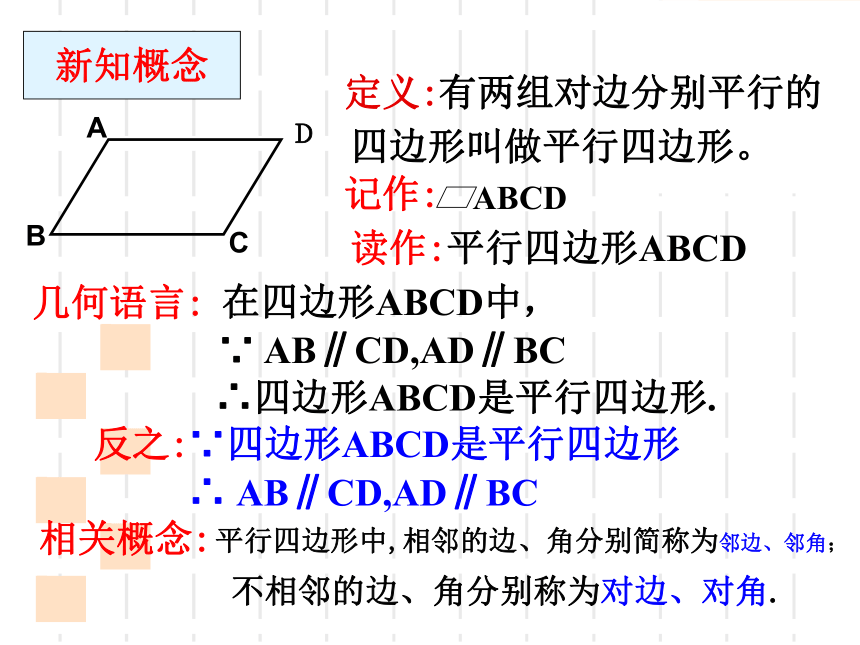
定义:
记作:
几何语言:
∴四边形ABCD是平行四边形.
ABCD
在四边形ABCD中,
读作:平行四边形ABCD
平行四边形中,相邻的边、角分别简称为邻边、邻角;
反之:
∴
AB∥CD,AD∥BC
A
B
D
C
有两组对边分别平行的
四边形叫做平行四边形。
新知概念
∵
AB∥CD,AD∥BC
∵四边形ABCD是平行四边形
相关概念:
不相邻的边、角分别称为对边、对角.
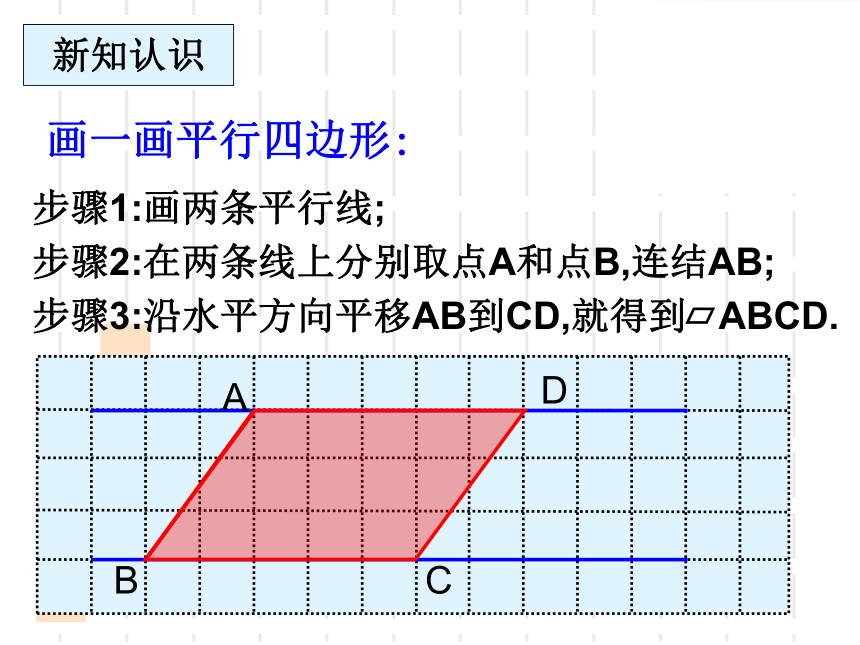
步骤3:沿水平方向平移AB到CD,就得到
ABCD.
A
B
C
D
步骤1:画两条平行线;
步骤2:在两条线上分别取点A和点B,连结AB;
新知认识
画一画平行四边形:
平行四边形的边、角有怎样的数量关系?
A
B
C
D
猜一猜
请用直尺,量角器等工具度量你手中平行四边形的边和角,并记录下数据,验证猜想AB=DC,AD=BC,∠A=∠C,∠B=∠D是否正确?
量一量
证一证
A
B
C
D
用你以前所学的知识证明猜想.
已知:
ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
A
B
C
D
证一证
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴
△ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
平行四边形的性质
几何语言:
定理1:平行四边形的对边相等
定理2:平行四边形的对角相等
∵
四边形ABCD是平行四边形
∴
AB=CD,AD=BC.(平行四边形的对边相等)
在 ABCD中,
AB=CD,AD=BC.(平行四边形的对边相等)
或
练习
1.在
ABCD中,
AB=3cm,BC=8cm,则 ABCD的周长
是
cm.
2. ABCD的周长为30cm,两邻边之比为2﹕1,则 ABCD
的两邻边长分别为 .
3.如图所示,四边形ABCD是平行四边形,若∠A=70°,则∠B=
。∠C=
;
∠D=
。
???????????
22
10cm,5cm
4、如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m.
A
B
C
D
⑵
若∠A+∠C=200°,
则∠A和∠B分别为多少度?
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC.
∵AB=8,
∴CD=8(m),
又AB+BC+CD+AD=36,
∴AD=BC=10(m).
解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∠A+∠B=180°.
∵∠A+∠C=200°,
∴∠A=100°,∠B=80°.
⑴
其他三条边各长多少?
观察发现
1,
如图是某区部分街道示意图,其中BC∥AD∥EG,AB//FH∥DC.图中的平行四边形共有_____个.
9
A
B
C
D
E
G
F
H
O
2,从B站乘车到D站只有两
条路线有直接到达的公交车,
路线1是B—E—A—F—D,
路线2是B—H—O—G—D,
请比较两条路线路程的长短,
并说明理由.
任画一个三角形,你能通过平移两边后,得到一个平行四边形吗?如果能得到平形四边形,那么能得到几个?分别用字母将它们表示出来。
A
B
C
D
E
F
画一画
哦也!胜利完成小练习!
1、平行四边形的定义:两组对边分别
平行的四边形叫做平行四边形.
2、平行四边形的性质:
平行四边形的对边平行且相等;
平行四边形的对角相等.相邻的内角互补。
感悟与收获
友情提示:
通常四边形问题要转化为三角形问题.
A
B
C
D
作业:
教材76页
1、2,3题,
教材80页的第1,
4题
谢谢!
平行四边形的性质
活动一
你能用你手中一对全等的三角形纸片拼出什么样的几何图形?
定义:
记作:
几何语言:
∴四边形ABCD是平行四边形.
ABCD
在四边形ABCD中,
读作:平行四边形ABCD
平行四边形中,相邻的边、角分别简称为邻边、邻角;
反之:
∴
AB∥CD,AD∥BC
A
B
D
C
有两组对边分别平行的
四边形叫做平行四边形。
新知概念
∵
AB∥CD,AD∥BC
∵四边形ABCD是平行四边形
相关概念:
不相邻的边、角分别称为对边、对角.
步骤3:沿水平方向平移AB到CD,就得到
ABCD.
A
B
C
D
步骤1:画两条平行线;
步骤2:在两条线上分别取点A和点B,连结AB;
新知认识
画一画平行四边形:
平行四边形的边、角有怎样的数量关系?
A
B
C
D
猜一猜
请用直尺,量角器等工具度量你手中平行四边形的边和角,并记录下数据,验证猜想AB=DC,AD=BC,∠A=∠C,∠B=∠D是否正确?
量一量
证一证
A
B
C
D
用你以前所学的知识证明猜想.
已知:
ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
A
B
C
D
证一证
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴
△ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
平行四边形的性质
几何语言:
定理1:平行四边形的对边相等
定理2:平行四边形的对角相等
∵
四边形ABCD是平行四边形
∴
AB=CD,AD=BC.(平行四边形的对边相等)
在 ABCD中,
AB=CD,AD=BC.(平行四边形的对边相等)
或
练习
1.在
ABCD中,
AB=3cm,BC=8cm,则 ABCD的周长
是
cm.
2. ABCD的周长为30cm,两邻边之比为2﹕1,则 ABCD
的两邻边长分别为 .
3.如图所示,四边形ABCD是平行四边形,若∠A=70°,则∠B=
。∠C=
;
∠D=
。
???????????
22
10cm,5cm
4、如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m.
A
B
C
D
⑵
若∠A+∠C=200°,
则∠A和∠B分别为多少度?
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC.
∵AB=8,
∴CD=8(m),
又AB+BC+CD+AD=36,
∴AD=BC=10(m).
解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∠A+∠B=180°.
∵∠A+∠C=200°,
∴∠A=100°,∠B=80°.
⑴
其他三条边各长多少?
观察发现
1,
如图是某区部分街道示意图,其中BC∥AD∥EG,AB//FH∥DC.图中的平行四边形共有_____个.
9
A
B
C
D
E
G
F
H
O
2,从B站乘车到D站只有两
条路线有直接到达的公交车,
路线1是B—E—A—F—D,
路线2是B—H—O—G—D,
请比较两条路线路程的长短,
并说明理由.
任画一个三角形,你能通过平移两边后,得到一个平行四边形吗?如果能得到平形四边形,那么能得到几个?分别用字母将它们表示出来。
A
B
C
D
E
F
画一画
哦也!胜利完成小练习!
1、平行四边形的定义:两组对边分别
平行的四边形叫做平行四边形.
2、平行四边形的性质:
平行四边形的对边平行且相等;
平行四边形的对角相等.相邻的内角互补。
感悟与收获
友情提示:
通常四边形问题要转化为三角形问题.
A
B
C
D
作业:
教材76页
1、2,3题,
教材80页的第1,
4题
谢谢!
