2020--2021学年沪科版 八年级数学下册19.4多边形的镶嵌(共46张ppt)
文档属性
| 名称 | 2020--2021学年沪科版 八年级数学下册19.4多边形的镶嵌(共46张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-05 00:00:00 | ||
图片预览











文档简介
(共46张PPT)
——花园初中
多边形的镶嵌
这些图形拼成一个平面图案的共同特征是什么?
平面镶嵌
定义:用形状相同或不同的平面封闭图形把一块平面既无缝隙又不重叠的全部覆盖叫平面镶嵌。
注意:镶嵌的原则是不重叠,又无空隙。
北京故宫御花园
花石子路镶嵌图案最多的园林
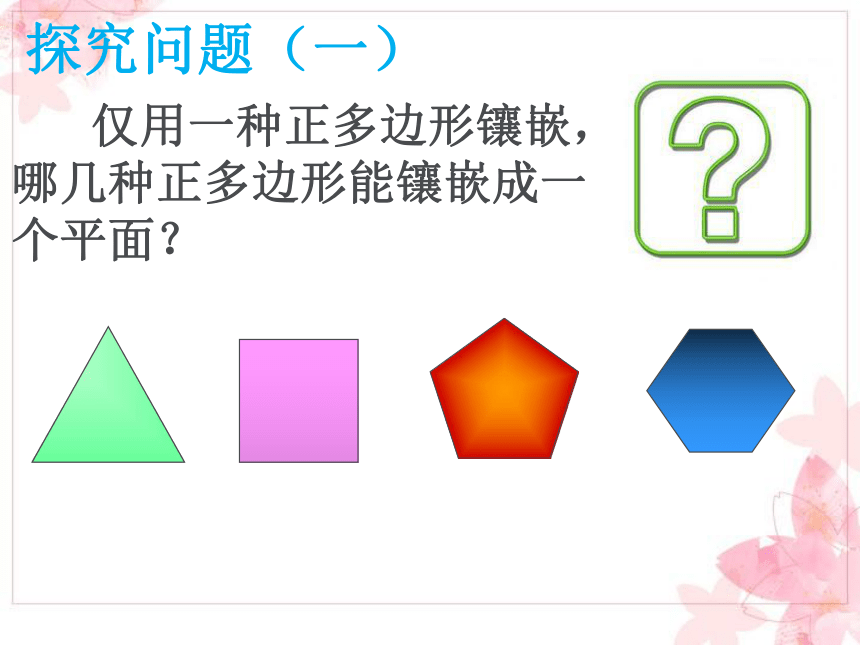
仅用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面?
探究问题(一)
分析:∵
∠1+∠2+∠3=108°×3=324°
∴
3个正五边形有缝隙
324°<
360°
4个正五边形有重叠108°×4=432°>
360°
1
2
3
正五边形不能镶嵌
6
60
0
90
0
108
0
120
0
4
3
3
4
能镶嵌
能镶嵌
不能镶嵌
有空隙
能镶嵌
60
×6=360
0
0
90
×4=360
0
0
108°×3<360°
108
×4>360
0
0
不能镶嵌
有重叠
收
集
整
理
正n边形
拼图
每个内角度数
多边形个数
结果
n=3
n=4
n=5
n=6
思考:仅限于同一种正多边形镶嵌,还能找到能镶嵌的其他正多边形吗?
120°×3=360°
探究问题(二)
思考
1、同一种任意三角形可否镶嵌成一个平面?
2、同一种任意四边形可否镶嵌成一个平面?
要求:学会动手操作,摆一摆!
结论
一般的三角形和四边形也可以作平面镶嵌。
注:若想实现连续铺设,还应将相等的边重合在一起。
用两种或三种正多边形进行镶嵌.
探究问题(三)
分析:设在接点处正三角形有x个,正方形有y个,正六边形有z个
∴60°x+90°y+120°z=360
°
即
x+1.5y+2z=6
整数解
正三角形x
正方形y
正六边形z
1
4
0
1
2
2
0
2
3
3
2
0
4
1
2
1
正多边形
拼
图
正三角形
和
正六边形
2×60°+
2×120°=360°
4×60°+
1×120°=360°
每个接点处用2个正方形和3个正三角形。
2×90°+3×60°=360°
正三角形和正方形的平面镶嵌
思考:正八边形和正方形能不能镶嵌?
更多的两种正多边形的镶嵌
正十二边形与正三角形的平面镶嵌
正八边形与正方形的平面镶嵌
正十边形与正五边形的平面镶嵌
三种正多边形的平面镶嵌
正三角形与正方形、正六边形的平面镶嵌
正十二边形与正方形、正六边形的平面镶嵌
两种或三种正多边形拼接在同一点的各个内角的和恰好等于360°,这两种或三种正多边形就能镶嵌。
注:平面镶嵌中,多边形内角和起着重要作用。
结论
1、平面镶嵌的定义。
注:无重叠、无缝隙
2、正多边形平面镶嵌的条件。
注:接点处为360°
3、关注身边的数学,关注数学中的美。
归纳总结
镶嵌图片欣赏:
镶嵌图片欣赏:
镶嵌之父
埃舍尔是荷兰的现代版画艺术家、“图形艺术家”,他是一个将艺术与数学融合的画家,着迷于各种镶嵌。许多数学家认为在他的作品中数学的原则和思想得到了非同寻常的形象化。他的作品几乎无人能及,世人尊称他为“镶嵌之父”。
。
埃舍尔的作品
埃舍尔的作品
埃舍尔的作品
埃舍尔的作品
埃舍尔的作品
埃舍尔的作品
不同视角看到
两种场景!
1.
用一种正多边形镶嵌,哪些可以,分别是哪些正多边形?
2.
用两种正多边形设计镶嵌图形。
课后作业
小
结
S
h
u
x
u
e
台州市书生中学朱仁江制作
谢谢光临指导
再见
——花园初中
多边形的镶嵌
这些图形拼成一个平面图案的共同特征是什么?
平面镶嵌
定义:用形状相同或不同的平面封闭图形把一块平面既无缝隙又不重叠的全部覆盖叫平面镶嵌。
注意:镶嵌的原则是不重叠,又无空隙。
北京故宫御花园
花石子路镶嵌图案最多的园林
仅用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面?
探究问题(一)
分析:∵
∠1+∠2+∠3=108°×3=324°
∴
3个正五边形有缝隙
324°<
360°
4个正五边形有重叠108°×4=432°>
360°
1
2
3
正五边形不能镶嵌
6
60
0
90
0
108
0
120
0
4
3
3
4
能镶嵌
能镶嵌
不能镶嵌
有空隙
能镶嵌
60
×6=360
0
0
90
×4=360
0
0
108°×3<360°
108
×4>360
0
0
不能镶嵌
有重叠
收
集
整
理
正n边形
拼图
每个内角度数
多边形个数
结果
n=3
n=4
n=5
n=6
思考:仅限于同一种正多边形镶嵌,还能找到能镶嵌的其他正多边形吗?
120°×3=360°
探究问题(二)
思考
1、同一种任意三角形可否镶嵌成一个平面?
2、同一种任意四边形可否镶嵌成一个平面?
要求:学会动手操作,摆一摆!
结论
一般的三角形和四边形也可以作平面镶嵌。
注:若想实现连续铺设,还应将相等的边重合在一起。
用两种或三种正多边形进行镶嵌.
探究问题(三)
分析:设在接点处正三角形有x个,正方形有y个,正六边形有z个
∴60°x+90°y+120°z=360
°
即
x+1.5y+2z=6
整数解
正三角形x
正方形y
正六边形z
1
4
0
1
2
2
0
2
3
3
2
0
4
1
2
1
正多边形
拼
图
正三角形
和
正六边形
2×60°+
2×120°=360°
4×60°+
1×120°=360°
每个接点处用2个正方形和3个正三角形。
2×90°+3×60°=360°
正三角形和正方形的平面镶嵌
思考:正八边形和正方形能不能镶嵌?
更多的两种正多边形的镶嵌
正十二边形与正三角形的平面镶嵌
正八边形与正方形的平面镶嵌
正十边形与正五边形的平面镶嵌
三种正多边形的平面镶嵌
正三角形与正方形、正六边形的平面镶嵌
正十二边形与正方形、正六边形的平面镶嵌
两种或三种正多边形拼接在同一点的各个内角的和恰好等于360°,这两种或三种正多边形就能镶嵌。
注:平面镶嵌中,多边形内角和起着重要作用。
结论
1、平面镶嵌的定义。
注:无重叠、无缝隙
2、正多边形平面镶嵌的条件。
注:接点处为360°
3、关注身边的数学,关注数学中的美。
归纳总结
镶嵌图片欣赏:
镶嵌图片欣赏:
镶嵌之父
埃舍尔是荷兰的现代版画艺术家、“图形艺术家”,他是一个将艺术与数学融合的画家,着迷于各种镶嵌。许多数学家认为在他的作品中数学的原则和思想得到了非同寻常的形象化。他的作品几乎无人能及,世人尊称他为“镶嵌之父”。
。
埃舍尔的作品
埃舍尔的作品
埃舍尔的作品
埃舍尔的作品
埃舍尔的作品
埃舍尔的作品
不同视角看到
两种场景!
1.
用一种正多边形镶嵌,哪些可以,分别是哪些正多边形?
2.
用两种正多边形设计镶嵌图形。
课后作业
小
结
S
h
u
x
u
e
台州市书生中学朱仁江制作
谢谢光临指导
再见
