几种不同增长的函数模型
图片预览


文档简介
(共20张PPT)
绍兴鲁迅中学
年龄
身高
课 堂 引 入
请同学们画出本人从出生到现在身高变化的大致图象.
例1、假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回 报比前一天翻一番.
回报量
选择投资方案的标准
X
请问:你会选择哪种投资方案?
日 回 报
累计回报
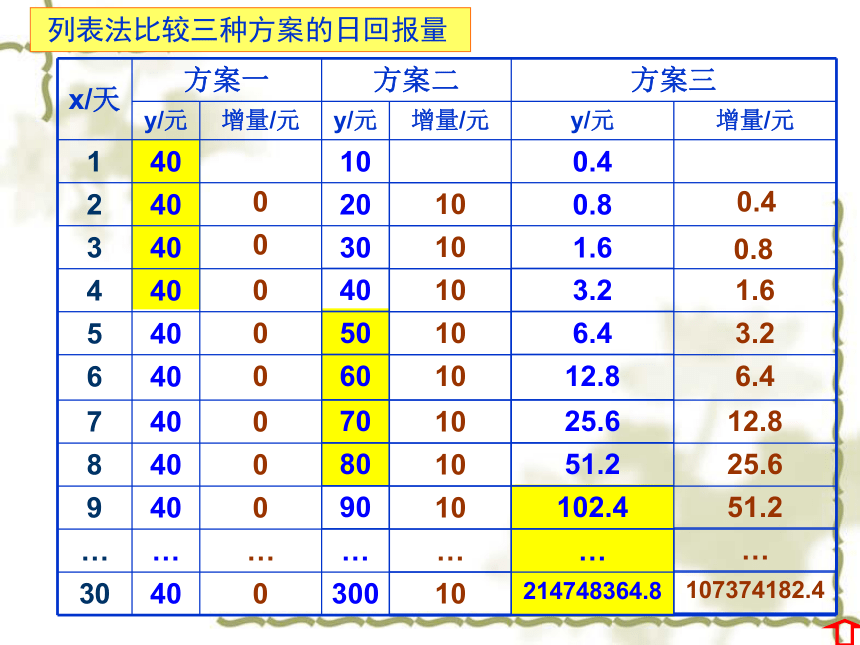
x/天 方案一 方案二 方案三
y/元 增量/元 y/元 增量/元 y/元 增量/元
1 40 10 0.4
2 40 20 0.8
3 40 30 1.6
4 40
5 40
6 40
7 40
8 40
9 40
… … … …
30 40 300 214748364.8
40
50
60
70
80
90
3.2
6.4
12.8
25.6
51.2
102.4
列表法比较三种方案的日回报量
0
0
0
0
0
0
0
0
…
0
10
10
10
10
10
10
10
10
…
10
0.4
0.8
1.6
3.2
6.4
12.8
25.6
51.2
…
107374182.4
结
论
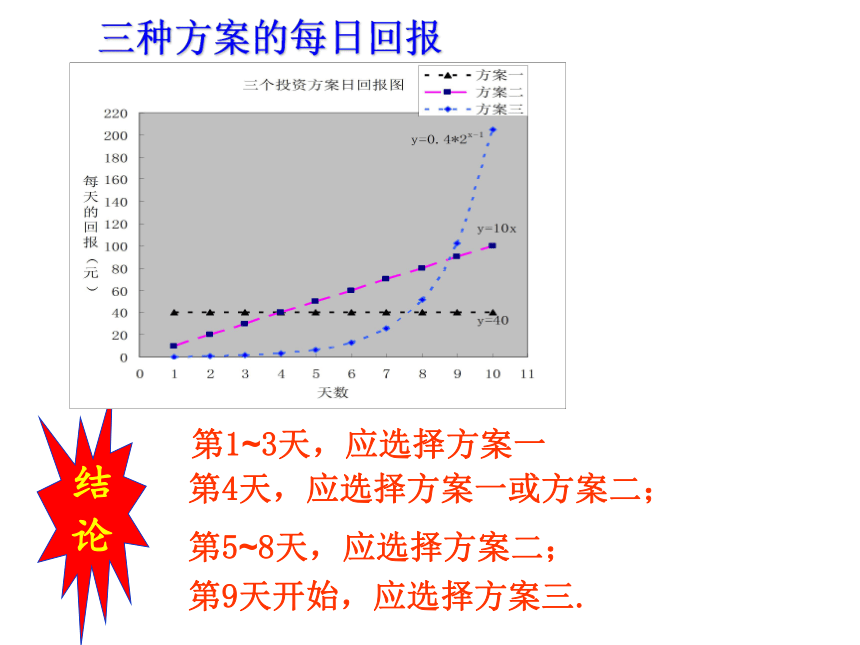
三种方案的每日回报
第1~3天,应选择方案一
第4天,应选择方案一或方案二;
第9天开始,应选择方案三.
第5~8天,应选择方案二;
819
409
204
102
50.8
25
12
6
2.8
1.2
0.4
三
660
550
450
360
280
210
150
100
60
30
10
二
440
400
360
320
280
240
200
160
120
80
40
一
11
10
9
8
7
6
5
4
3
2
1
天数
回报/元
方案
3276
1638
910
780
520
480
13
12
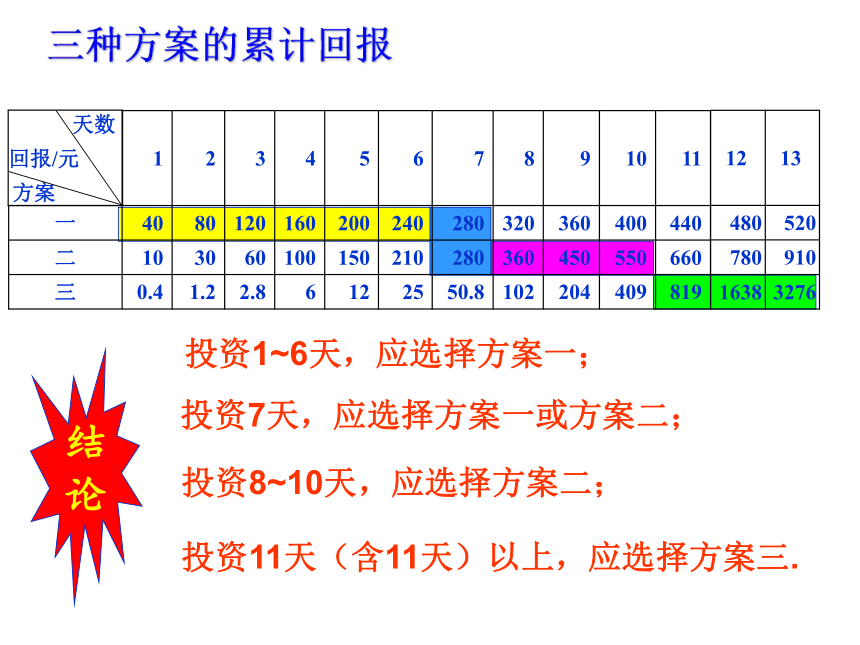
三种方案的累计回报
投资1~6天,应选择方案一;
投资7天,应选择方案一或方案二;
投资8~10天,应选择方案二;
投资11天(含11天)以上,应选择方案三.
结
论
1
2
3
4
6
5
7
8
9
10
20
0
40
60
80
100
120
140
y
x 方案一:y=40
1
2
3
4
5
6
7
8
9
10
…
40
40
40
40
40
40
40
40
40
40
…
x 方案二
y=10x
1
2
3
4
5
6
7
8
9
10
…
10
20
30
40
50
60
70
80
90
100
…
x y=0.4*2x-1
1
2
3
4
5
6
7
8
9
10
…
0.4
0.8
1.6
3.2
6.4
12.8
25.6
51.2
102.4
204.8
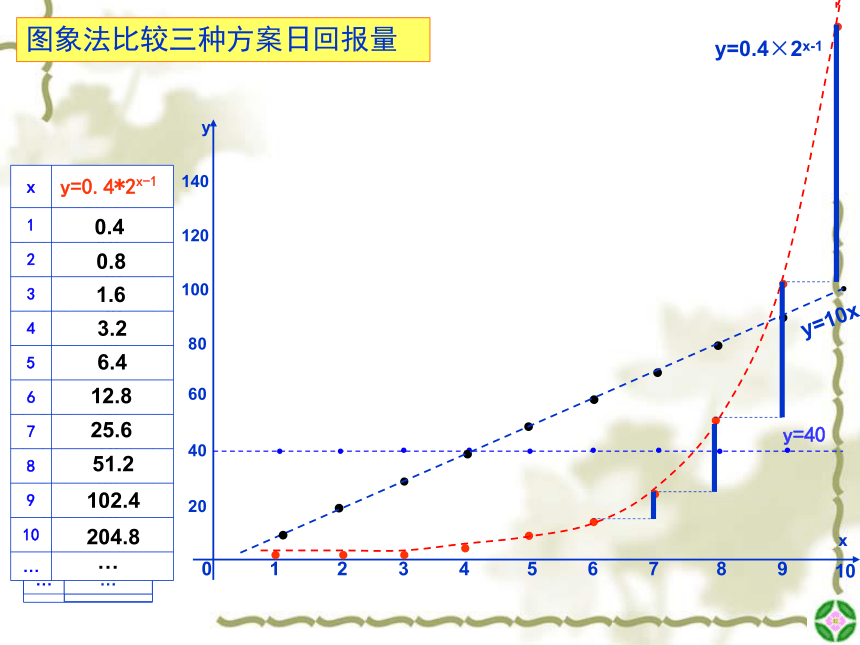
图象法比较三种方案日回报量
y=40
y=10x
y=0.4×2x-1
x
…
常数函数 一次函数 指数型函数
几种常见函数的增长情况:
保持不变
直线上升
匀速增长
急剧增长
指数爆炸
没有增长
列表法
图象法
实际问题
数学问题
函数问题
读懂题意
抽象概括
解析法
X
例2、公司为了实现1000万元利润的目标,准备制定了一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随着销售利润x (单位:万元)的增加而增加,但奖金数不超过5万元,同时奖金不超过利润的25%。现有三个奖励模型:
y=0.25x, y=log7x+1, y=1.002x ,
其中哪个模型能符合公司的要求?
X
例2、某公司2009年为了实现1000万元总利润的目标,他准备制定一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随着销售利润x (单位:万元)的增加而增加,但奖金数不超过5万元,同时奖金不超过利润的25%。现有三个奖励模型:y=0.25x,y=log7x+1,y=1.002x,其中哪个模型能符合公司的要求呢?
思考:本题中符合公司要求的
模型有什么条件
销售利润X的取值范围:
奖金y满足的条件:
三种奖金模型的函数模型
x y=0.25x y=log7x+1 y=1.002x
100
200
300
400
500
600
700
800
900
1000
0.1
0.08
0.07
0.06
0.05
125
150
175
200
225
250
4.19
4.29
2.72
3.32
4.05
4.95
6.04
7.37
25
25
25
25
25
25
25
25
25
0.27
0.33
0.4
0.5
0.6
0.73
0.9
1.09
1.33
增量△y
增量△y
增量△y
25
50
75
100
4.37
4.44
4.5
4.55
0.35
0.21
0.15
0.11
3.37
3.72
3.93
4.08
1.22
1.49
1.82
2.22
对数增长模型:平缓增长
观察—归纳—猜想—证明
200
400
600
800
1000
2
3
4
5
6
7
8
1
0
这个奖励方案实施以后,立刻调动了员工的积极性,企业发展蒸蒸日上,但随着时间的推移,又出现了新的问题,员工缺乏创造高销售额的积极性……
X
200
400
600
800
1000
2
3
4
5
6
7
8
1
0
10万~ 50万,奖金不超过2万
50万~ 200万,奖金不超过4万
200万~ 1000万, 奖金不超过20万
为了实现1000万元利润的目标,在销售利润
达到10万元时,按销售利润进行奖励,且奖金y
(单位:万元)随着销售利润x (单位:万元)的增
加而增加,要求如下:
X
请选择适当的函数模型,用图象表达你的设计方案.(四人团队合作完成)
创新设计
O
x
y
O
x
y
O
x
y
x
O
y
O
200
50
10
1000
20
4
2
1.请同学谈谈你对几类不同增长的函数模型(一次函数、指数函数、对数函数)差异的认识。
2. 几类增长函数建模的步骤
列解析式
具体问题
画出图像(形)
列出表格(数)
不同增长
确定模型
预报和决策
控制和优化
3. 你还有其他感悟吗?
随 堂 小结
常数函数 一次函数 指数函数 对数函数
增长量为零 增长量相同 增长量迅速增加 增长量减少
没有增长
直线增长
指数爆炸
对数增长
x 0 5 10 15 20 25 30
y1 5 130 505 1130 2005 3130 4505
y2 5 94.478 1785.2 33733 6.37×105 1.2×107 2.28×108
y3 5 30 55 80 105 130 155
y4 5 2.3107 1.4295 1.1407 1.0461 1.0151 1.005
随 堂 练 习
1.四个变量y1,y2,y3,y4随变量x变化的数据如下表:
关于x成指数型变化的变量是__________
关于x成直线型变化的变量是__________
y3
2.观察下表,某人身高用一次函数、指数型函数、对数型函数哪个刻画比较好,为什么?
y2
某人年龄和身高(cm)
年龄 21 23 25 27
身高 160 162 163 163.5
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么!
——毕达哥拉斯
绍兴鲁迅中学
年龄
身高
课 堂 引 入
请同学们画出本人从出生到现在身高变化的大致图象.
例1、假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回 报比前一天翻一番.
回报量
选择投资方案的标准
X
请问:你会选择哪种投资方案?
日 回 报
累计回报
x/天 方案一 方案二 方案三
y/元 增量/元 y/元 增量/元 y/元 增量/元
1 40 10 0.4
2 40 20 0.8
3 40 30 1.6
4 40
5 40
6 40
7 40
8 40
9 40
… … … …
30 40 300 214748364.8
40
50
60
70
80
90
3.2
6.4
12.8
25.6
51.2
102.4
列表法比较三种方案的日回报量
0
0
0
0
0
0
0
0
…
0
10
10
10
10
10
10
10
10
…
10
0.4
0.8
1.6
3.2
6.4
12.8
25.6
51.2
…
107374182.4
结
论
三种方案的每日回报
第1~3天,应选择方案一
第4天,应选择方案一或方案二;
第9天开始,应选择方案三.
第5~8天,应选择方案二;
819
409
204
102
50.8
25
12
6
2.8
1.2
0.4
三
660
550
450
360
280
210
150
100
60
30
10
二
440
400
360
320
280
240
200
160
120
80
40
一
11
10
9
8
7
6
5
4
3
2
1
天数
回报/元
方案
3276
1638
910
780
520
480
13
12
三种方案的累计回报
投资1~6天,应选择方案一;
投资7天,应选择方案一或方案二;
投资8~10天,应选择方案二;
投资11天(含11天)以上,应选择方案三.
结
论
1
2
3
4
6
5
7
8
9
10
20
0
40
60
80
100
120
140
y
x 方案一:y=40
1
2
3
4
5
6
7
8
9
10
…
40
40
40
40
40
40
40
40
40
40
…
x 方案二
y=10x
1
2
3
4
5
6
7
8
9
10
…
10
20
30
40
50
60
70
80
90
100
…
x y=0.4*2x-1
1
2
3
4
5
6
7
8
9
10
…
0.4
0.8
1.6
3.2
6.4
12.8
25.6
51.2
102.4
204.8
图象法比较三种方案日回报量
y=40
y=10x
y=0.4×2x-1
x
…
常数函数 一次函数 指数型函数
几种常见函数的增长情况:
保持不变
直线上升
匀速增长
急剧增长
指数爆炸
没有增长
列表法
图象法
实际问题
数学问题
函数问题
读懂题意
抽象概括
解析法
X
例2、公司为了实现1000万元利润的目标,准备制定了一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随着销售利润x (单位:万元)的增加而增加,但奖金数不超过5万元,同时奖金不超过利润的25%。现有三个奖励模型:
y=0.25x, y=log7x+1, y=1.002x ,
其中哪个模型能符合公司的要求?
X
例2、某公司2009年为了实现1000万元总利润的目标,他准备制定一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随着销售利润x (单位:万元)的增加而增加,但奖金数不超过5万元,同时奖金不超过利润的25%。现有三个奖励模型:y=0.25x,y=log7x+1,y=1.002x,其中哪个模型能符合公司的要求呢?
思考:本题中符合公司要求的
模型有什么条件
销售利润X的取值范围:
奖金y满足的条件:
三种奖金模型的函数模型
x y=0.25x y=log7x+1 y=1.002x
100
200
300
400
500
600
700
800
900
1000
0.1
0.08
0.07
0.06
0.05
125
150
175
200
225
250
4.19
4.29
2.72
3.32
4.05
4.95
6.04
7.37
25
25
25
25
25
25
25
25
25
0.27
0.33
0.4
0.5
0.6
0.73
0.9
1.09
1.33
增量△y
增量△y
增量△y
25
50
75
100
4.37
4.44
4.5
4.55
0.35
0.21
0.15
0.11
3.37
3.72
3.93
4.08
1.22
1.49
1.82
2.22
对数增长模型:平缓增长
观察—归纳—猜想—证明
200
400
600
800
1000
2
3
4
5
6
7
8
1
0
这个奖励方案实施以后,立刻调动了员工的积极性,企业发展蒸蒸日上,但随着时间的推移,又出现了新的问题,员工缺乏创造高销售额的积极性……
X
200
400
600
800
1000
2
3
4
5
6
7
8
1
0
10万~ 50万,奖金不超过2万
50万~ 200万,奖金不超过4万
200万~ 1000万, 奖金不超过20万
为了实现1000万元利润的目标,在销售利润
达到10万元时,按销售利润进行奖励,且奖金y
(单位:万元)随着销售利润x (单位:万元)的增
加而增加,要求如下:
X
请选择适当的函数模型,用图象表达你的设计方案.(四人团队合作完成)
创新设计
O
x
y
O
x
y
O
x
y
x
O
y
O
200
50
10
1000
20
4
2
1.请同学谈谈你对几类不同增长的函数模型(一次函数、指数函数、对数函数)差异的认识。
2. 几类增长函数建模的步骤
列解析式
具体问题
画出图像(形)
列出表格(数)
不同增长
确定模型
预报和决策
控制和优化
3. 你还有其他感悟吗?
随 堂 小结
常数函数 一次函数 指数函数 对数函数
增长量为零 增长量相同 增长量迅速增加 增长量减少
没有增长
直线增长
指数爆炸
对数增长
x 0 5 10 15 20 25 30
y1 5 130 505 1130 2005 3130 4505
y2 5 94.478 1785.2 33733 6.37×105 1.2×107 2.28×108
y3 5 30 55 80 105 130 155
y4 5 2.3107 1.4295 1.1407 1.0461 1.0151 1.005
随 堂 练 习
1.四个变量y1,y2,y3,y4随变量x变化的数据如下表:
关于x成指数型变化的变量是__________
关于x成直线型变化的变量是__________
y3
2.观察下表,某人身高用一次函数、指数型函数、对数型函数哪个刻画比较好,为什么?
y2
某人年龄和身高(cm)
年龄 21 23 25 27
身高 160 162 163 163.5
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么!
——毕达哥拉斯
