山东省聊城市东昌府区2020-2021学年八年级下学期期中考试数学试题(word版 含答案)
文档属性
| 名称 | 山东省聊城市东昌府区2020-2021学年八年级下学期期中考试数学试题(word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-05 00:00:00 | ||
图片预览


文档简介
山东省聊城市东昌府区2020-2021学年八年级下学期期中考试
数学试题
(时间∶120
分钟;满分∶120分)
选择题(本题共12个小题,每小题3分,共36分,在每小题给出的四个选项中,只有一项正确)
1.下列语句正确的是()
A.4
是
16
的算术平方根,即±=4
B.-3是
27
的立方根
C.的立方根是2
D.1
的立方根是-1
2.若a
>b,则下列不等式成立的是()
A.
3a
<
3b
B.na
>
nb
C.-1>-1
D.-a>-b
3.实数-1,,0121212…,-,,π,,,0.3
中,无理数的个数有(
)A.2个
B.3个
C.4个
D.5个
4.下列命题∶①一组对边平行,另一组对边相等的四边形是平行四边形;②对角线互相垂直且平分的四边形是菱形;③一个角为90°且一组邻边相等的四边形是正方形;④对角线相等的平行四边形是矩形.其中真命题的个数是(
)
A.1
B.2
C.3
D:4
5.如图,数轴上的点A
所表示的数为a,则a的值为
A.1+
B.
C.-1+
D.1-
如图,在正方形ABCD中,AB=3,点E,F分别在边AB,CD上,
∠EFD=60°.若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则BE
的长度为()
A.1
B.
C.
D.2
2-x>1
7.不等式组
的解集,在数轴上表示正确的是()
2x
+4
≥0
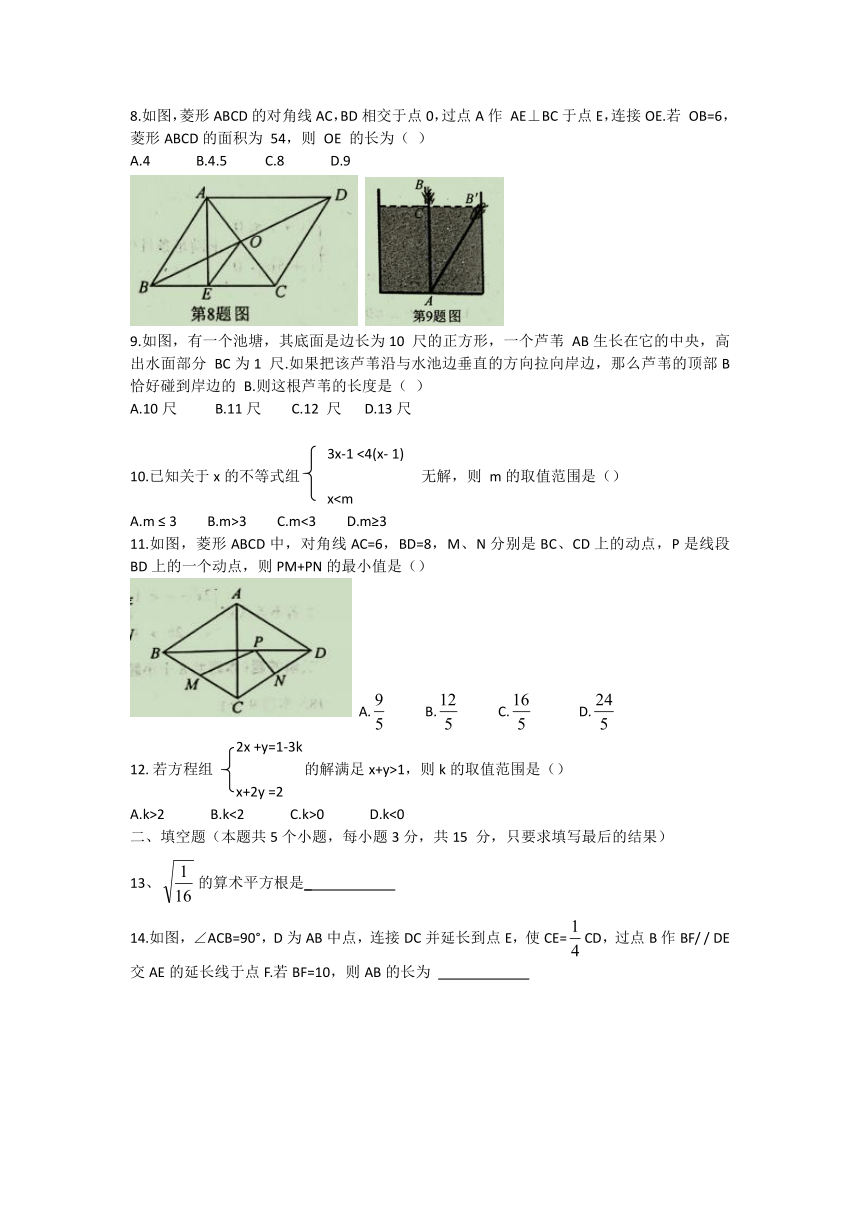
8.如图,菱形ABCD的对角线AC,BD相交于点0,过点A作
AE⊥BC于点E,连接OE.若
OB=6,菱形ABCD的面积为
54,则
OE
的长为(
)
A.4
B.4.5
C.8
D.9
9.如图,有一个池塘,其底面是边长为10
尺的正方形,一个芦苇
AB生长在它的中央,高出水面部分
BC为1
尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的
B.则这根芦苇的长度是(
)
A.10尺
B.11尺
C.12
尺
D.13尺
3x-1
<4(x-
1)
10.已知关于x的不等式组
无解,则
m的取值范围是()
xA.m
≤
3
B.m>3
C.m<3
D.m≥3
11.如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的动点,P是线段BD上的一个动点,则PM+PN的最小值是()
A.
B.
C.
D.
2x
+y=1-3k
若方程组
的解满足x+y>1,则k的取值范围是()
x+2y
=2
A.k>2
B.k<2
C.k>0
D.k<0
二、填空题(本题共5个小题,每小题3分,共15
分,只要求填写最后的结果)
13、的算术平方根是_
14.如图,∠ACB=90°,D为AB中点,连接DC并延长到点E,使CE=CD,过点B作BF/
/
DE交AE的延长线于点F.若BF=10,则AB的长为
15.观察下列各式∶
.........
请你将猜想到的规律用自然数n的代数式表示出来∶_
16.2002年8月在北京召开的国际数学大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图),如果大正方形的面积是25,小正方形的面积是1,直角三角形较短的直角边为a,较长的直角边为b,那么(a+b)?的值为_____
2x-a
<
1
若不等式组
的解集为-1x-
2b
>
3
三、解答题(本题共8个小题,共69
分,解答应写出文字说明、证明过程或推演步骤)
18.(本题9
分)
(1)计算∶+I-2I
(2)解不等式-1≤,并把解集在数轴上表示出来.
5x+
2
>
3(x
-1)
(3)解不等式组∶
,把解集在数轴上表示出来.并求出其中的负整数解
x-1≤7-x
19.(本题8
分)如图,已知点
C是线段
BD上的一点,∠B=∠D=90°,若AB=3,BC=2,CD=6,DE
=4,
AE
=
.
(1)
求
AC、CE
的长
(2)求证∶∠ACE
=
90°.
20.(本题8分)某商店欲购进A、B两种商品,若购进A种商品5件和B种商品4件需300
元;若购进A
种商品
6
件和
B种商品
8
件需
440
元;
(1)求
A、B
两种商品每件的进价分别为多少元?
(2)商店准备用不超过1625元购进50件这两种商品,求购进A种商品最多是多少件?
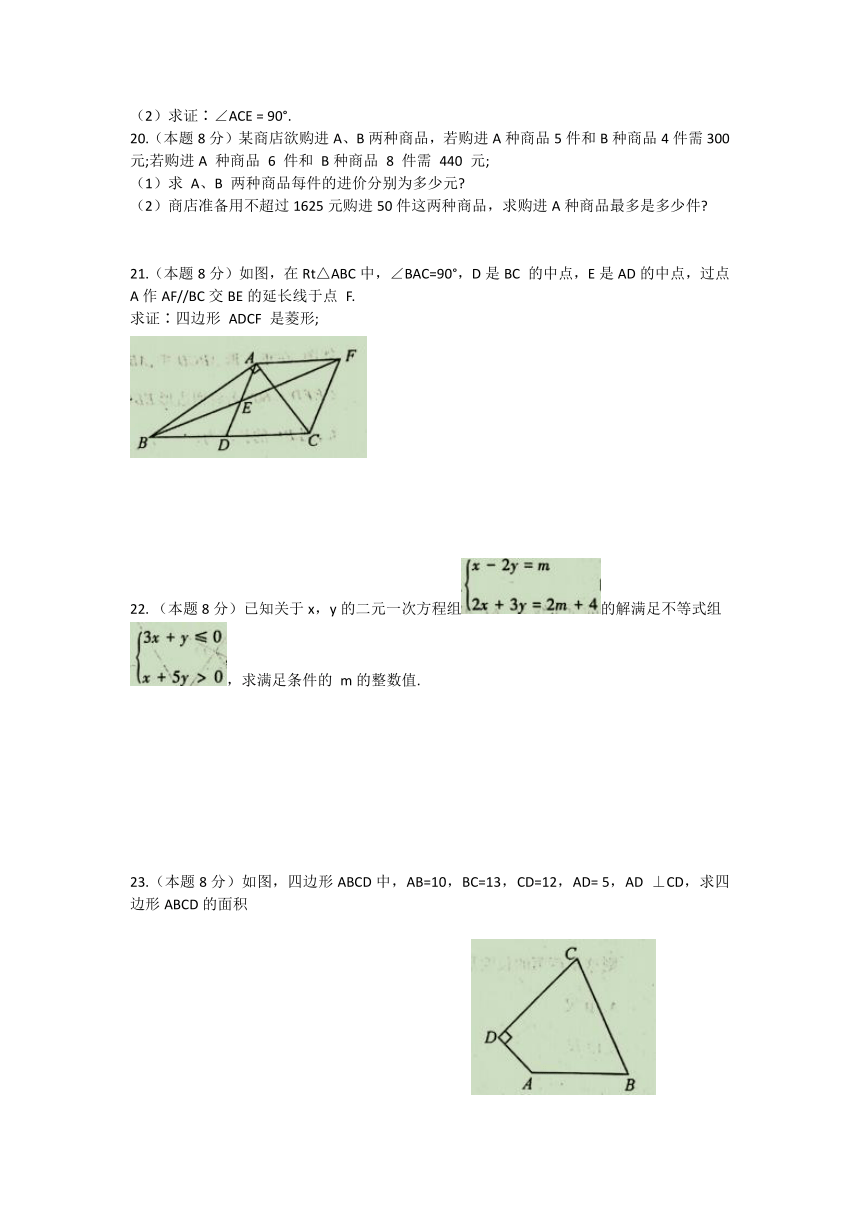
21.(本题8分)如图,在Rt△ABC中,∠BAC=90°,D是BC
的中点,E是AD的中点,过点A作AF//BC交BE的延长线于点
F.
求证∶四边形
ADCF
是菱形;
(本题8分)已知关于x,y的二元一次方程组的解满足不等式组
,求满足条件的
m的整数值.
23.(本题8分)如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=
5,AD
⊥CD,求四边形ABCD的面积
24.(本题8分)如图,在ABCD中;对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接
CG.
(1)求证∶△ABE
△CDF
(2)当AB与AC满足什么数量关系时,四边形
EGCF是矩形?请说明理由.
25.(本题12分)如图,已知
△ABC为等边三角形,CF//AB,点P为线段
AB上任意一点(点P不与
A、B重合),过点
P作PE
//BC,分别交AC、CF于
G、E∶
(1)四边形
PBCE
是平行四边形吗?,为什么?
(2)连结
PC、AE,求证∶CP=
AE;
(3)试探索∶当P为AB的中点时,四边形APCE是什么样的特殊四边形·并说明理由.
数学试题
(时间∶120
分钟;满分∶120分)
选择题(本题共12个小题,每小题3分,共36分,在每小题给出的四个选项中,只有一项正确)
1.下列语句正确的是()
A.4
是
16
的算术平方根,即±=4
B.-3是
27
的立方根
C.的立方根是2
D.1
的立方根是-1
2.若a
>b,则下列不等式成立的是()
A.
3a
<
3b
B.na
>
nb
C.-1>-1
D.-a>-b
3.实数-1,,0121212…,-,,π,,,0.3
中,无理数的个数有(
)A.2个
B.3个
C.4个
D.5个
4.下列命题∶①一组对边平行,另一组对边相等的四边形是平行四边形;②对角线互相垂直且平分的四边形是菱形;③一个角为90°且一组邻边相等的四边形是正方形;④对角线相等的平行四边形是矩形.其中真命题的个数是(
)
A.1
B.2
C.3
D:4
5.如图,数轴上的点A
所表示的数为a,则a的值为
A.1+
B.
C.-1+
D.1-
如图,在正方形ABCD中,AB=3,点E,F分别在边AB,CD上,
∠EFD=60°.若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则BE
的长度为()
A.1
B.
C.
D.2
2-x>1
7.不等式组
的解集,在数轴上表示正确的是()
2x
+4
≥0
8.如图,菱形ABCD的对角线AC,BD相交于点0,过点A作
AE⊥BC于点E,连接OE.若
OB=6,菱形ABCD的面积为
54,则
OE
的长为(
)
A.4
B.4.5
C.8
D.9
9.如图,有一个池塘,其底面是边长为10
尺的正方形,一个芦苇
AB生长在它的中央,高出水面部分
BC为1
尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的
B.则这根芦苇的长度是(
)
A.10尺
B.11尺
C.12
尺
D.13尺
3x-1
<4(x-
1)
10.已知关于x的不等式组
无解,则
m的取值范围是()
x
≤
3
B.m>3
C.m<3
D.m≥3
11.如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的动点,P是线段BD上的一个动点,则PM+PN的最小值是()
A.
B.
C.
D.
2x
+y=1-3k
若方程组
的解满足x+y>1,则k的取值范围是()
x+2y
=2
A.k>2
B.k<2
C.k>0
D.k<0
二、填空题(本题共5个小题,每小题3分,共15
分,只要求填写最后的结果)
13、的算术平方根是_
14.如图,∠ACB=90°,D为AB中点,连接DC并延长到点E,使CE=CD,过点B作BF/
/
DE交AE的延长线于点F.若BF=10,则AB的长为
15.观察下列各式∶
.........
请你将猜想到的规律用自然数n的代数式表示出来∶_
16.2002年8月在北京召开的国际数学大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图),如果大正方形的面积是25,小正方形的面积是1,直角三角形较短的直角边为a,较长的直角边为b,那么(a+b)?的值为_____
2x-a
<
1
若不等式组
的解集为-1
2b
>
3
三、解答题(本题共8个小题,共69
分,解答应写出文字说明、证明过程或推演步骤)
18.(本题9
分)
(1)计算∶+I-2I
(2)解不等式-1≤,并把解集在数轴上表示出来.
5x+
2
>
3(x
-1)
(3)解不等式组∶
,把解集在数轴上表示出来.并求出其中的负整数解
x-1≤7-x
19.(本题8
分)如图,已知点
C是线段
BD上的一点,∠B=∠D=90°,若AB=3,BC=2,CD=6,DE
=4,
AE
=
.
(1)
求
AC、CE
的长
(2)求证∶∠ACE
=
90°.
20.(本题8分)某商店欲购进A、B两种商品,若购进A种商品5件和B种商品4件需300
元;若购进A
种商品
6
件和
B种商品
8
件需
440
元;
(1)求
A、B
两种商品每件的进价分别为多少元?
(2)商店准备用不超过1625元购进50件这两种商品,求购进A种商品最多是多少件?
21.(本题8分)如图,在Rt△ABC中,∠BAC=90°,D是BC
的中点,E是AD的中点,过点A作AF//BC交BE的延长线于点
F.
求证∶四边形
ADCF
是菱形;
(本题8分)已知关于x,y的二元一次方程组的解满足不等式组
,求满足条件的
m的整数值.
23.(本题8分)如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=
5,AD
⊥CD,求四边形ABCD的面积
24.(本题8分)如图,在ABCD中;对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接
CG.
(1)求证∶△ABE
△CDF
(2)当AB与AC满足什么数量关系时,四边形
EGCF是矩形?请说明理由.
25.(本题12分)如图,已知
△ABC为等边三角形,CF//AB,点P为线段
AB上任意一点(点P不与
A、B重合),过点
P作PE
//BC,分别交AC、CF于
G、E∶
(1)四边形
PBCE
是平行四边形吗?,为什么?
(2)连结
PC、AE,求证∶CP=
AE;
(3)试探索∶当P为AB的中点时,四边形APCE是什么样的特殊四边形·并说明理由.
同课章节目录
