(北师大版)六年级数学下册课件 反比例
图片预览







文档简介
(共27张PPT)
反比例
1.结合丰富的实例,认识反比例。
2.能根据反比例的意义,判断两个相关联的量是不是成反比例。
3.利用反比例解决一些简单的生活 问题,感受反比例关系在生活中的广泛应用。
教学目标
正比例关系的意义是什么 怎样用字母表示这种关系
判断两种相关联量成不成正比例的关键是什么
判断下面各题中的两种量是否成正比例?为什么?
(1)工作效率一定,工作时间和工作总量。
(2)每头奶牛的产奶量一定,奶牛的头数和产奶总量。
(3)正方形的边长和它的面积。
(4)每袋水泥质量相同,水泥的袋数与总质量.
在加法表上把和是12的方格圈起来,可连成一条直线。
12 13 14 15 16 17 18 19 20 21 22 23 24
11 12 13 14 15 16 17 18 19 20 21 22 23
10 11 12 13 14 15 16 17 18 19 20 21 22
9 10 11 12 13 14 15 16 17 18 19 20 21
8 9 10 11 12 13 14 15 16 17 18 19 20
7 8 9 10 11 12 13 14 15 16 17 18 19
6 7 8 9 10 11 12 13 14 15 16 17 18
5 6 7 8 9 10 11 12 13 14 15 16 17
4 5 6 7 8 9 10 11 12 13 14 15 16
3 4 5 6 7 8 9 10 11 12 13 14 15
2 3 4 5 6 7 8 9 10 11 12 13 14
1 2 3 4 5 6 7 8 9 10 11 12 13
+ 1 2 3 4 5 6 7 8 9 10 11 12
3+9=12
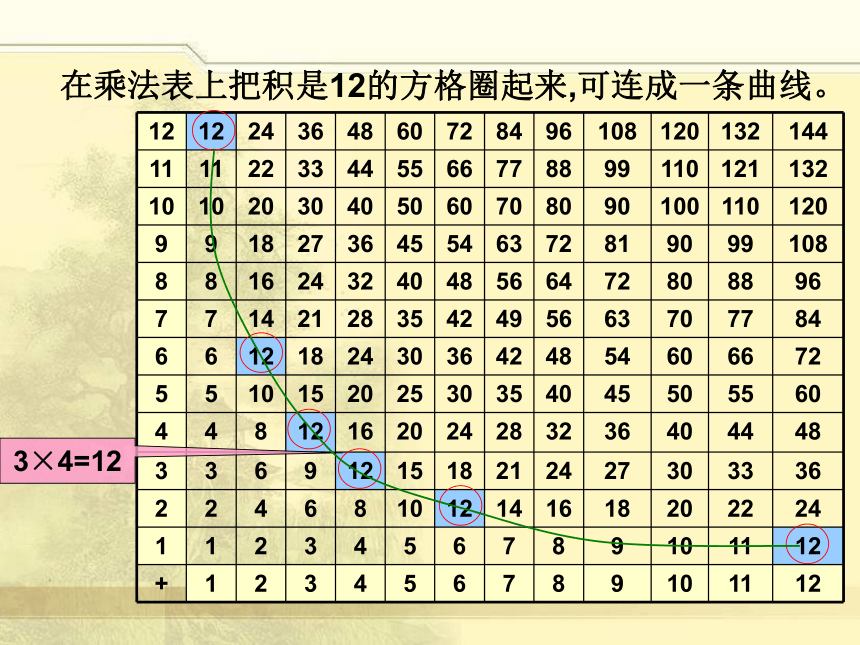
在乘法表上把积是12的方格圈起来,可连成一条曲线。
12 12 24 36 48 60 72 84 96 108 120 132 144
11 11 22 33 44 55 66 77 88 99 110 121 132
10 10 20 30 40 50 60 70 80 90 100 110 120
9 9 18 27 36 45 54 63 72 81 90 99 108
8 8 16 24 32 40 48 56 64 72 80 88 96
7 7 14 21 28 35 42 49 56 63 70 77 84
6 6 12 18 24 30 36 42 48 54 60 66 72
5 5 10 15 20 25 30 35 40 45 50 55 60
4 4 8 12 16 20 24 28 32 36 40 44 48
3 3 6 9 12 15 18 21 24 27 30 33 36
2 2 4 6 8 10 12 14 16 18 20 22 24
1 1 2 3 4 5 6 7 8 9 10 11 12
+ 1 2 3 4 5 6 7 8 9 10 11 12
3×4=12
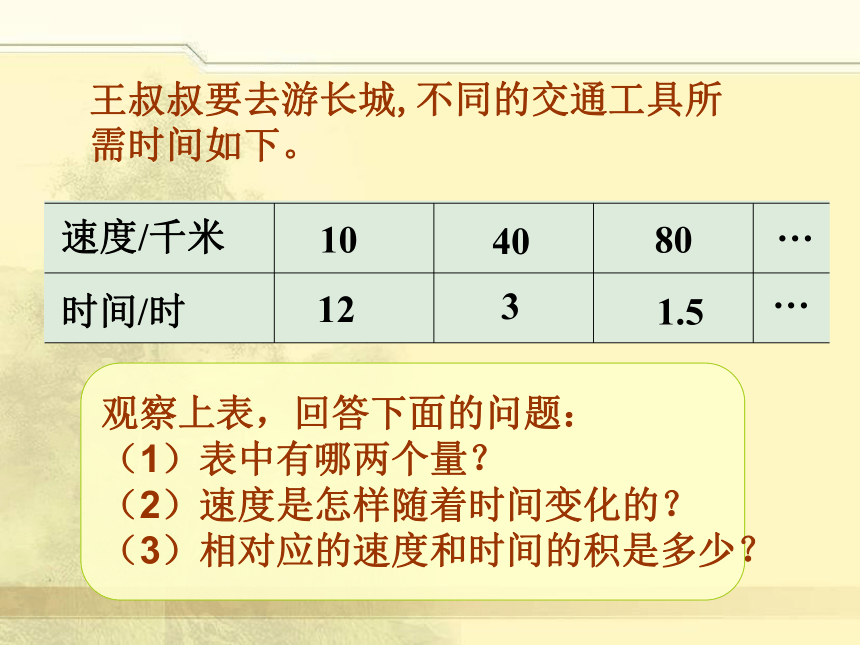
王叔叔要去游长城,不同的交通工具所需时间如下。
速度/千米
时间/时
10
40
80
12
3
1.5
…
…
观察上表,回答下面的问题:
(1)表中有哪两个量?
(2)速度是怎样随着时间变化的?
(3)相对应的速度和时间的积是多少?
速度是10,时间是12;
速度是40,时间是3;
速度是80,时间是1.5;
速度和所需时间是两种相关联的量,所需时间是随着速度的变化而变化的。
速度扩大,所需时间缩小。
速度缩小,所需时间扩大。
速度和所需时间的积总是一定的:
10×12=120
(1)表中的两种量是速度和时间;
(2)速度扩大,所需的时间反而
缩小;速度缩小,所需的时
间反而扩大。
(3)每两个相对应的数的乘积都是120。
40×3=120
80×1.5=120
速度和所需时间的积总是一定的:
10×12=120
40×3=120
80×1.5=120
(一定)
速度×时间=路程
有600毫升果汁,可平均分成若干杯。请把下表填完整
分的杯数/杯
每杯的果汁量/ml
6
5
4
3
2
100
…
…
120
15
200
300
(1)表中有哪两种量?
表中有每杯的果汁量和分的杯数两种量。
(2)分的杯数是怎样随着每杯的果汁量变化的
每杯的果汁量扩大,分的杯数反而缩小。
每杯的果汁量缩小,分的杯数反而扩大。
每杯的果汁量和分的杯数的积是一定的
(3)它们的关系是什么?
每杯的果汁量× 分的杯数= 果汁总量(一定)
有600毫升果汁,可平均分成若干杯。请把下表填完整
分的杯数/杯
每杯的果汁量/ml
6
5
4
3
2
100
…
…
120
15
200
300
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
(一定)
速度×时间=路程
每杯的果汁量× 分的杯数= 果汁总量(一定)
如果用x和y表示两种相关联的量,用k表示它们的积,那么上面这种数量关系式可以怎样写呢
X×Y=K(一定)
判定方法:
判定两个量是不是成反比例,主
要是看它们的积是不是一定的。
8
6
4
3
每天看的页数×看完全书所需天数=总页数(一定)
60
40
30
总字数不变
30×80÷24=100(个)
打字所用时间随打字速度的变化而变化,并且它们的乘积一定,所以打字所用时间和速度成反比例。
打字的速度×打字所用的时间=总字数(一定)
判断下面每题中的两种量是不是成反比例,并说明理由。
煤的总量一定,每天的烧煤量和能够烧的天数。
张伯伯骑自行车从家到县城,
骑自行车的速度和所需的时间。
判断下面每题中的两种量是不是成反比例,并说明理由。
生产电视机的总台数一定,每天生产的台数和所用的天数。
判断下面每题中的两种量是不是成反比例,并说明理由。
长方形的面积一定,它的长和宽。
判断下面每题中的两种量是不是成反比例,并说明理由。
铺地面积一定,方砖边长与所需块数。
判断下面每题中的两种量是不是成反比例,并说明理由。
每天的烧煤量(kg)
20 40 50 100
烧煤的天数 50 25 20 10
1.下表中的两个量成反比例吗 为什么
2. 用36个边长为1cm的正方形拼一个长方形,把所拼成的长方形的长和宽填入下面的表格
长(cm)
宽(cm)
在上表中长和宽成反比例吗? 说明理由。
3.判断下面各题中的两种量是否成反比例。
(1)长方形的面积一定,它的长和宽。
(2)圆的直径和它的周长。
(3)长方体的体积一定,它的底面积和高。
(4)糊纸盒的总个数一定,每人糊的个数 和人数。
(5)三角形的面积一定,它的底和高。
(6)单价一定,总价和数量。
本节课主要学习了反比例关系,要求同学们对照正比例关系,掌握什么样的两个量才是成反比例的量,什么 叫做反比例关系!并能解决反比例的实际问题。
反比例
1.结合丰富的实例,认识反比例。
2.能根据反比例的意义,判断两个相关联的量是不是成反比例。
3.利用反比例解决一些简单的生活 问题,感受反比例关系在生活中的广泛应用。
教学目标
正比例关系的意义是什么 怎样用字母表示这种关系
判断两种相关联量成不成正比例的关键是什么
判断下面各题中的两种量是否成正比例?为什么?
(1)工作效率一定,工作时间和工作总量。
(2)每头奶牛的产奶量一定,奶牛的头数和产奶总量。
(3)正方形的边长和它的面积。
(4)每袋水泥质量相同,水泥的袋数与总质量.
在加法表上把和是12的方格圈起来,可连成一条直线。
12 13 14 15 16 17 18 19 20 21 22 23 24
11 12 13 14 15 16 17 18 19 20 21 22 23
10 11 12 13 14 15 16 17 18 19 20 21 22
9 10 11 12 13 14 15 16 17 18 19 20 21
8 9 10 11 12 13 14 15 16 17 18 19 20
7 8 9 10 11 12 13 14 15 16 17 18 19
6 7 8 9 10 11 12 13 14 15 16 17 18
5 6 7 8 9 10 11 12 13 14 15 16 17
4 5 6 7 8 9 10 11 12 13 14 15 16
3 4 5 6 7 8 9 10 11 12 13 14 15
2 3 4 5 6 7 8 9 10 11 12 13 14
1 2 3 4 5 6 7 8 9 10 11 12 13
+ 1 2 3 4 5 6 7 8 9 10 11 12
3+9=12
在乘法表上把积是12的方格圈起来,可连成一条曲线。
12 12 24 36 48 60 72 84 96 108 120 132 144
11 11 22 33 44 55 66 77 88 99 110 121 132
10 10 20 30 40 50 60 70 80 90 100 110 120
9 9 18 27 36 45 54 63 72 81 90 99 108
8 8 16 24 32 40 48 56 64 72 80 88 96
7 7 14 21 28 35 42 49 56 63 70 77 84
6 6 12 18 24 30 36 42 48 54 60 66 72
5 5 10 15 20 25 30 35 40 45 50 55 60
4 4 8 12 16 20 24 28 32 36 40 44 48
3 3 6 9 12 15 18 21 24 27 30 33 36
2 2 4 6 8 10 12 14 16 18 20 22 24
1 1 2 3 4 5 6 7 8 9 10 11 12
+ 1 2 3 4 5 6 7 8 9 10 11 12
3×4=12
王叔叔要去游长城,不同的交通工具所需时间如下。
速度/千米
时间/时
10
40
80
12
3
1.5
…
…
观察上表,回答下面的问题:
(1)表中有哪两个量?
(2)速度是怎样随着时间变化的?
(3)相对应的速度和时间的积是多少?
速度是10,时间是12;
速度是40,时间是3;
速度是80,时间是1.5;
速度和所需时间是两种相关联的量,所需时间是随着速度的变化而变化的。
速度扩大,所需时间缩小。
速度缩小,所需时间扩大。
速度和所需时间的积总是一定的:
10×12=120
(1)表中的两种量是速度和时间;
(2)速度扩大,所需的时间反而
缩小;速度缩小,所需的时
间反而扩大。
(3)每两个相对应的数的乘积都是120。
40×3=120
80×1.5=120
速度和所需时间的积总是一定的:
10×12=120
40×3=120
80×1.5=120
(一定)
速度×时间=路程
有600毫升果汁,可平均分成若干杯。请把下表填完整
分的杯数/杯
每杯的果汁量/ml
6
5
4
3
2
100
…
…
120
15
200
300
(1)表中有哪两种量?
表中有每杯的果汁量和分的杯数两种量。
(2)分的杯数是怎样随着每杯的果汁量变化的
每杯的果汁量扩大,分的杯数反而缩小。
每杯的果汁量缩小,分的杯数反而扩大。
每杯的果汁量和分的杯数的积是一定的
(3)它们的关系是什么?
每杯的果汁量× 分的杯数= 果汁总量(一定)
有600毫升果汁,可平均分成若干杯。请把下表填完整
分的杯数/杯
每杯的果汁量/ml
6
5
4
3
2
100
…
…
120
15
200
300
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
(一定)
速度×时间=路程
每杯的果汁量× 分的杯数= 果汁总量(一定)
如果用x和y表示两种相关联的量,用k表示它们的积,那么上面这种数量关系式可以怎样写呢
X×Y=K(一定)
判定方法:
判定两个量是不是成反比例,主
要是看它们的积是不是一定的。
8
6
4
3
每天看的页数×看完全书所需天数=总页数(一定)
60
40
30
总字数不变
30×80÷24=100(个)
打字所用时间随打字速度的变化而变化,并且它们的乘积一定,所以打字所用时间和速度成反比例。
打字的速度×打字所用的时间=总字数(一定)
判断下面每题中的两种量是不是成反比例,并说明理由。
煤的总量一定,每天的烧煤量和能够烧的天数。
张伯伯骑自行车从家到县城,
骑自行车的速度和所需的时间。
判断下面每题中的两种量是不是成反比例,并说明理由。
生产电视机的总台数一定,每天生产的台数和所用的天数。
判断下面每题中的两种量是不是成反比例,并说明理由。
长方形的面积一定,它的长和宽。
判断下面每题中的两种量是不是成反比例,并说明理由。
铺地面积一定,方砖边长与所需块数。
判断下面每题中的两种量是不是成反比例,并说明理由。
每天的烧煤量(kg)
20 40 50 100
烧煤的天数 50 25 20 10
1.下表中的两个量成反比例吗 为什么
2. 用36个边长为1cm的正方形拼一个长方形,把所拼成的长方形的长和宽填入下面的表格
长(cm)
宽(cm)
在上表中长和宽成反比例吗? 说明理由。
3.判断下面各题中的两种量是否成反比例。
(1)长方形的面积一定,它的长和宽。
(2)圆的直径和它的周长。
(3)长方体的体积一定,它的底面积和高。
(4)糊纸盒的总个数一定,每人糊的个数 和人数。
(5)三角形的面积一定,它的底和高。
(6)单价一定,总价和数量。
本节课主要学习了反比例关系,要求同学们对照正比例关系,掌握什么样的两个量才是成反比例的量,什么 叫做反比例关系!并能解决反比例的实际问题。
