湖北省新高考联考协作体2020-2021学年高一下学期期中联考数学试题 Word版含解析
文档属性
| 名称 | 湖北省新高考联考协作体2020-2021学年高一下学期期中联考数学试题 Word版含解析 |

|
|
| 格式 | docx | ||
| 文件大小 | 712.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-05 00:00:00 | ||
图片预览




文档简介
2021年湖北省新高考联考协作体高一下学期期中考试
高一数学试卷
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合false第二象限角false,false钝角false,false小于180°的角false,则A,B,C关系正确的是( )
A.false B.false C.false D. false
2.已知复数false,false为false的共轭复数,复数false,则下列结论正确的是( )
A. false对应的点在复平面的第二象限 B. false
C. false的实部为1 D. false的虚部为false
3.已知false,下列命题为真命题的是( )
A. 若false,则false B. 若false,false,则false
C. 若false,false,则false D. 若false,且false则false
4. 若false为有一个角是false的等腰三角形,false,且|false|=|false|=2,
那么false( )
A.12+false B.10 C.14 D. false
5. 十七世纪德国著名的天文学家开普勒曾经这样说过:“几何学里有两件宝,一个是勾股定理,另一个是黄金分割.”黄金三角形有两种,中底与腰之比为黄金分割比的黄金三角形被认为是最美的三角形,它
是一个顶角为false的等腰三角形(另一种是顶角为false的等腰三角形).
例如,五角星由五个黄金三角形与一个正五边形组成,如图所示,在其中一个黄金false中,false根据这些信息,可得false( )
A.false B. false C. false D. false
6. 若在false中,false是false边上的点,且满足false,false=false,则 false=( )
A.false B.false C. false D.0
7. 已知false1,false1,false1,则实数false的取值范围为( )
A.(0,false) B.(0 , 1) C.false D.false
8. 将函数false的图象向右平移false个单位,得到函数false的图象,若false为偶函数,则下列结论:(1) false的图象的一条对称轴为false;(2)false的图象的一个对称中心为false;(3) false在区间false上单调递增,正确的个数是( )
A. 0 B.1 C.2 D.3
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9.对于任意两个向量false和false,下列命题中正确的是( )
A.若false,false满足|false|>|false|,且false与false反向,则falseB.false
C.false
D.false
10. 函数false有且只有一个零点的一个充分不必要条件是( )
A.false B.false C.false D.false
11. 设false,false是复数,则下列说法中正确的是 ( )
A. 若false,则false B. 若false,则false
C. 若false,则false D. 若false,则false
12. 下列说法错误的是( )
A. 若点G为false的重心,则false
B. 若false,则存在唯一实数false使得false
C. 已知false,且false与false的夹角为锐角,则实数false的取值
范围是false
D. 若非零向量false,且false,则false为等边三角形
三、填空题:本大题共4小题,每小题5分,共20分.
13. 已知向量false,若A,B,D三点共线,则false______.
14. 已知false,则false的最小值为 ,此时false为 .
15. 我们知道,函数false的图象关于坐标原点成中心对称图形的充要条件是函数false为奇函数,有同学发现可以将其推广为:函数false的图象关于点P(a,b)
成中心对称图形的充要条件是函数false为奇函数.
根据该推广结论,则函数false图象的对称中心坐标为 .
16. 已知a,b,c分别是false三个内角A,B,C的对边,①若false,则false是等腰三角形;②若false,则false是等腰三角形;③false,则false是锐角三角形;4若false=false ,则false是等边三角形,以上四个命题中正确的是 .
四、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.
17. 在平面直角坐标系false中,已知点false.
(1)以线段false为邻边作平行四边形ABCD,求向量false的坐标和false;
(2)设实数t满足false,求t的值
18. 已知命题p:false,q:false,使不等式false成立.
(1)若q为真命题,求实数m的取值范围;
(2)若false和q有且只有一个为真命题,求实数m的取值范围.
19. 若函数false为偶函数,当false时,false.
(1)求函数false的表达式,画出函数false的图象;
(2)若函数false在区间false上单调递减,求实数false的取值范围.
20. 在锐角false中,false分别是false所对的边,已知false,向量false,
false,且false .
(1)求角A的大小
(2)求false周长的取值范围.
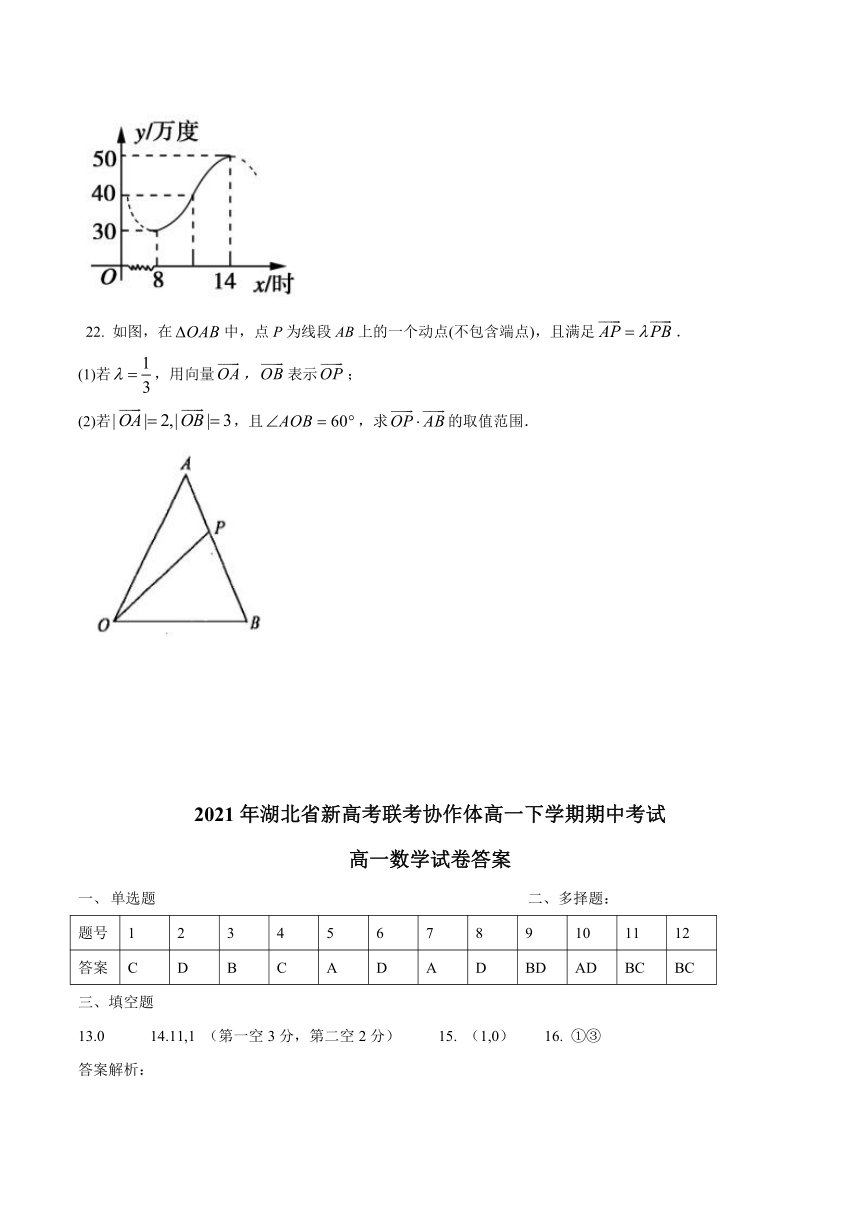
21. 某地一天用电量y (单位:万度)随时间false(单位:时)的变化曲线近似满足函数false(false),其部分图象如图所示.
(1)写出这段曲线的函数解析式;
(2)请问在该天的哪段时间该地用电量不超过35万度?
22. 如图,在false中,点P为线段AB上的一个动点(不包含端点),且满足false.
(1)若false,用向量false,false表示false;
(2)若false,且false,求false的取值范围.
2021年湖北省新高考联考协作体高一下学期期中考试
高一数学试卷答案
一、 单选题 二、多择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D
B
C
A
D
A
D
BD
AD
BC
BC
三、填空题
13.0 14.11,1 (第一空3分,第二空2分) 15. (1,0) 16. ①③
答案解析:
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.由题意得false,故A错误;A与C互不包含,故B错误;因为false,所以false,故C正确;由以上分析可知D错误.故选C.
2. false, false, 选D.
3. false若false则false,A不正确;
B:因为false,false,则false,所以false,故B正确;
C:当false时,可得不等式不成立,故C不正确.
D:false且false,若false,则false,D不正确,故选B.
4.∵ 在false 中,|false|=|false|=2,falsefalsefalse, 故选C.
5. (方法一)由图形知,false,且false,false,
false,
false.故选A.
(方法二)由图形知,false,false,
false.故选A.
6.false, 在false中AD=3BD,如图所示
设BD=x(x>0),则AD=3x,AC=2-3x,BC=2-x,
易知cos∠ADC=-cos∠BDC.
∴false,
解得x=,故AD=1,AC=1,∴cosA=false=0. 故选D.
7.①由false1,得false
②由false1,得false
③由false1,得false,
∴false1, false1, false 1,同时成立取交集得false,故选A.
8. false(false)的图象向右平移false个单位得false
若false为偶函数,且false,∴false,故可得false,
当xfalse时,false,由正弦函数图象可得(1)(2)(3)都正确,
故选D
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9. A项,向量不能比较大小,错误. C项,false,错误. 故选BD
10. ∵函数f(x)过点(1,0),
∴函数f(x)有且只有一个零点?函数y=false (x≤0)没有零点?函数y=false(x≤0)的图象与直线y=false没有公共点.数形结合可得false≤0或false>1.结合选项故选AD.
11. A项,若false,则false,故错误;
B项,若false,则false和false互为共轭复数,所以false,故正确;
C项,若false,则false,false,故正确;
D项,若false,则false,而false,故错误.
故选BC.
12. A项,已知G为重心,则false,false,false,
false.故正确;
B项, 若false,则实数false不唯一,故错误;
C项,已知false,且false与false的夹角为锐角,
可得false,即false,可得false,解得false,
当false与false的夹角为0时,falsefalse,所以false,
所以false与false的夹角为锐角时,false且false,故错误;
D项,因为false为与false同向的单位向量,false为与false同向的单位向量,所以false表示向量false,false角平分线所在的向量,根据false,知向量false,false角平分线所在的向量垂直于false,所以为等腰三角形.根据false,知false,false的夹角为false,所以是等边三角形.
故说法错误的是BC.
三、填空题:本大题共4小题,每小题5分,共20分.
13. ∵向量false,false,false,
false,
∴A,B,D三点共线,false ,false,解得false.
故答案为: 0 .
14.false,
false,
当且仅当false,即false时取最小值.
故答案为: 11 , 1 .
15.令false
false
false
∵false为奇函数,false ,即false,解得false
故答案为: (1,0)
16.①由acosC+ccosA=a及正弦定理,可知sinAcosC+sinCcosA=sinA,
∴sinA=sinB,∴A=B,∴选项①正确;
②由acosA=bcosB及正弦定理,可得sin2A=sin2B,∴A=B或A+B=,
∴△ABC是等腰三角形或直角三角形,∴选项②错;
③∵tanA+tanB+tanC=tanAtanBtanC>0,∴A,B,C均为锐角,∴选项③正确;
4∵cos2false=false,cos2false=false,∴(1+cosB)·c=a+c,∴a=cosB·c=false,
∴2a2=a2+c2-b2,∴a2+b2=c2,∴△ABC为直角三角形.∴选项4不正确;
故答案为: ① ③
四、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.
17. 解:(1)∵由题意知false,
false ………………3分
false; ……………………………………5分
(2))由题意知:false,
由false,
得:false,
false,
false. ……………………………………10分
18.解:(1)∵false,使得false,
∴false,使得false.
设false
false,则false.
∴当q为真命题时,false. ……………………………………5分
(2)∵函数false在false上为增函数,
故在false上,f(x)的最大值为false.
false,∴false,
∴当p为真命题时m≥false ……………………………………7分
又∵p和q有且只有一个为真命题,∴p与q中一真一假,
①当p真q假时,false解得false.……………………………………9分
②当q真p假时,false解得false……………………………………11分
综上,m的取值范围是false ……………………………………12分
19. 解:(1)当false时,false,false.
由false是偶函数,得false.
所以false. …………………………………3分
函数false的图象,如图.
…………………………………6分
(2)由图象可知,函数false的单调递减区间是false和false. …………………8分
要使false在false上单调递减,
则false,解得false,
所以实数a的取值范围是false. …………………………………12分
20.解:(1)因为false且false,
所以false,得false
又因为false,所以false. …………………4分
(2)由正弦定理可得false ,得false……………6分
则false
false, …………………………………9分
∵false是锐角三角形,∴false,解得false ……10分
false,false,false,
∴false周长的取值范围为false …………………………12分
21.解(1)由图知false,所以false, …………………2分
又由图象可得半周期为6,false,故false, ………3分
又当false时,false,false ,false.
又false false
故false. ……………………5分
(2)由false,得false
false…………………………8分
false ………………………10分
false
因此,该天的6~10时和18~22时该地用电量不超过35万度 ……………12分
22 . 解:(1)若false,则false,
false,
false,
则false. …………………………4分
(2)false,
false,
false,
false, …………………………6分
false,且false
false,
false
false
false. …………………………10分
false ,false,
false的取值范围为false. …………………………12分
高一数学试卷
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合false第二象限角false,false钝角false,false小于180°的角false,则A,B,C关系正确的是( )
A.false B.false C.false D. false
2.已知复数false,false为false的共轭复数,复数false,则下列结论正确的是( )
A. false对应的点在复平面的第二象限 B. false
C. false的实部为1 D. false的虚部为false
3.已知false,下列命题为真命题的是( )
A. 若false,则false B. 若false,false,则false
C. 若false,false,则false D. 若false,且false则false
4. 若false为有一个角是false的等腰三角形,false,且|false|=|false|=2,
那么false( )
A.12+false B.10 C.14 D. false
5. 十七世纪德国著名的天文学家开普勒曾经这样说过:“几何学里有两件宝,一个是勾股定理,另一个是黄金分割.”黄金三角形有两种,中底与腰之比为黄金分割比的黄金三角形被认为是最美的三角形,它
是一个顶角为false的等腰三角形(另一种是顶角为false的等腰三角形).
例如,五角星由五个黄金三角形与一个正五边形组成,如图所示,在其中一个黄金false中,false根据这些信息,可得false( )
A.false B. false C. false D. false
6. 若在false中,false是false边上的点,且满足false,false=false,则 false=( )
A.false B.false C. false D.0
7. 已知false1,false1,false1,则实数false的取值范围为( )
A.(0,false) B.(0 , 1) C.false D.false
8. 将函数false的图象向右平移false个单位,得到函数false的图象,若false为偶函数,则下列结论:(1) false的图象的一条对称轴为false;(2)false的图象的一个对称中心为false;(3) false在区间false上单调递增,正确的个数是( )
A. 0 B.1 C.2 D.3
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9.对于任意两个向量false和false,下列命题中正确的是( )
A.若false,false满足|false|>|false|,且false与false反向,则false
C.false
D.false
10. 函数false有且只有一个零点的一个充分不必要条件是( )
A.false B.false C.false D.false
11. 设false,false是复数,则下列说法中正确的是 ( )
A. 若false,则false B. 若false,则false
C. 若false,则false D. 若false,则false
12. 下列说法错误的是( )
A. 若点G为false的重心,则false
B. 若false,则存在唯一实数false使得false
C. 已知false,且false与false的夹角为锐角,则实数false的取值
范围是false
D. 若非零向量false,且false,则false为等边三角形
三、填空题:本大题共4小题,每小题5分,共20分.
13. 已知向量false,若A,B,D三点共线,则false______.
14. 已知false,则false的最小值为 ,此时false为 .
15. 我们知道,函数false的图象关于坐标原点成中心对称图形的充要条件是函数false为奇函数,有同学发现可以将其推广为:函数false的图象关于点P(a,b)
成中心对称图形的充要条件是函数false为奇函数.
根据该推广结论,则函数false图象的对称中心坐标为 .
16. 已知a,b,c分别是false三个内角A,B,C的对边,①若false,则false是等腰三角形;②若false,则false是等腰三角形;③false,则false是锐角三角形;4若false=false ,则false是等边三角形,以上四个命题中正确的是 .
四、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.
17. 在平面直角坐标系false中,已知点false.
(1)以线段false为邻边作平行四边形ABCD,求向量false的坐标和false;
(2)设实数t满足false,求t的值
18. 已知命题p:false,q:false,使不等式false成立.
(1)若q为真命题,求实数m的取值范围;
(2)若false和q有且只有一个为真命题,求实数m的取值范围.
19. 若函数false为偶函数,当false时,false.
(1)求函数false的表达式,画出函数false的图象;
(2)若函数false在区间false上单调递减,求实数false的取值范围.
20. 在锐角false中,false分别是false所对的边,已知false,向量false,
false,且false .
(1)求角A的大小
(2)求false周长的取值范围.
21. 某地一天用电量y (单位:万度)随时间false(单位:时)的变化曲线近似满足函数false(false),其部分图象如图所示.
(1)写出这段曲线的函数解析式;
(2)请问在该天的哪段时间该地用电量不超过35万度?
22. 如图,在false中,点P为线段AB上的一个动点(不包含端点),且满足false.
(1)若false,用向量false,false表示false;
(2)若false,且false,求false的取值范围.
2021年湖北省新高考联考协作体高一下学期期中考试
高一数学试卷答案
一、 单选题 二、多择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D
B
C
A
D
A
D
BD
AD
BC
BC
三、填空题
13.0 14.11,1 (第一空3分,第二空2分) 15. (1,0) 16. ①③
答案解析:
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.由题意得false,故A错误;A与C互不包含,故B错误;因为false,所以false,故C正确;由以上分析可知D错误.故选C.
2. false, false, 选D.
3. false若false则false,A不正确;
B:因为false,false,则false,所以false,故B正确;
C:当false时,可得不等式不成立,故C不正确.
D:false且false,若false,则false,D不正确,故选B.
4.∵ 在false 中,|false|=|false|=2,falsefalsefalse, 故选C.
5. (方法一)由图形知,false,且false,false,
false,
false.故选A.
(方法二)由图形知,false,false,
false.故选A.
6.false, 在false中AD=3BD,如图所示
设BD=x(x>0),则AD=3x,AC=2-3x,BC=2-x,
易知cos∠ADC=-cos∠BDC.
∴false,
解得x=,故AD=1,AC=1,∴cosA=false=0. 故选D.
7.①由false1,得false
②由false1,得false
③由false1,得false,
∴false1, false1, false 1,同时成立取交集得false,故选A.
8. false(false)的图象向右平移false个单位得false
若false为偶函数,且false,∴false,故可得false,
当xfalse时,false,由正弦函数图象可得(1)(2)(3)都正确,
故选D
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9. A项,向量不能比较大小,错误. C项,false,错误. 故选BD
10. ∵函数f(x)过点(1,0),
∴函数f(x)有且只有一个零点?函数y=false (x≤0)没有零点?函数y=false(x≤0)的图象与直线y=false没有公共点.数形结合可得false≤0或false>1.结合选项故选AD.
11. A项,若false,则false,故错误;
B项,若false,则false和false互为共轭复数,所以false,故正确;
C项,若false,则false,false,故正确;
D项,若false,则false,而false,故错误.
故选BC.
12. A项,已知G为重心,则false,false,false,
false.故正确;
B项, 若false,则实数false不唯一,故错误;
C项,已知false,且false与false的夹角为锐角,
可得false,即false,可得false,解得false,
当false与false的夹角为0时,falsefalse,所以false,
所以false与false的夹角为锐角时,false且false,故错误;
D项,因为false为与false同向的单位向量,false为与false同向的单位向量,所以false表示向量false,false角平分线所在的向量,根据false,知向量false,false角平分线所在的向量垂直于false,所以为等腰三角形.根据false,知false,false的夹角为false,所以是等边三角形.
故说法错误的是BC.
三、填空题:本大题共4小题,每小题5分,共20分.
13. ∵向量false,false,false,
false,
∴A,B,D三点共线,false ,false,解得false.
故答案为: 0 .
14.false,
false,
当且仅当false,即false时取最小值.
故答案为: 11 , 1 .
15.令false
false
false
∵false为奇函数,false ,即false,解得false
故答案为: (1,0)
16.①由acosC+ccosA=a及正弦定理,可知sinAcosC+sinCcosA=sinA,
∴sinA=sinB,∴A=B,∴选项①正确;
②由acosA=bcosB及正弦定理,可得sin2A=sin2B,∴A=B或A+B=,
∴△ABC是等腰三角形或直角三角形,∴选项②错;
③∵tanA+tanB+tanC=tanAtanBtanC>0,∴A,B,C均为锐角,∴选项③正确;
4∵cos2false=false,cos2false=false,∴(1+cosB)·c=a+c,∴a=cosB·c=false,
∴2a2=a2+c2-b2,∴a2+b2=c2,∴△ABC为直角三角形.∴选项4不正确;
故答案为: ① ③
四、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.
17. 解:(1)∵由题意知false,
false ………………3分
false; ……………………………………5分
(2))由题意知:false,
由false,
得:false,
false,
false. ……………………………………10分
18.解:(1)∵false,使得false,
∴false,使得false.
设false
false,则false.
∴当q为真命题时,false. ……………………………………5分
(2)∵函数false在false上为增函数,
故在false上,f(x)的最大值为false.
false,∴false,
∴当p为真命题时m≥false ……………………………………7分
又∵p和q有且只有一个为真命题,∴p与q中一真一假,
①当p真q假时,false解得false.……………………………………9分
②当q真p假时,false解得false……………………………………11分
综上,m的取值范围是false ……………………………………12分
19. 解:(1)当false时,false,false.
由false是偶函数,得false.
所以false. …………………………………3分
函数false的图象,如图.
…………………………………6分
(2)由图象可知,函数false的单调递减区间是false和false. …………………8分
要使false在false上单调递减,
则false,解得false,
所以实数a的取值范围是false. …………………………………12分
20.解:(1)因为false且false,
所以false,得false
又因为false,所以false. …………………4分
(2)由正弦定理可得false ,得false……………6分
则false
false, …………………………………9分
∵false是锐角三角形,∴false,解得false ……10分
false,false,false,
∴false周长的取值范围为false …………………………12分
21.解(1)由图知false,所以false, …………………2分
又由图象可得半周期为6,false,故false, ………3分
又当false时,false,false ,false.
又false false
故false. ……………………5分
(2)由false,得false
false…………………………8分
false ………………………10分
false
因此,该天的6~10时和18~22时该地用电量不超过35万度 ……………12分
22 . 解:(1)若false,则false,
false,
false,
则false. …………………………4分
(2)false,
false,
false,
false, …………………………6分
false,且false
false,
false
false
false. …………………………10分
false ,false,
false的取值范围为false. …………………………12分
同课章节目录
