正弦函数的性质和图像

(共21张PPT)
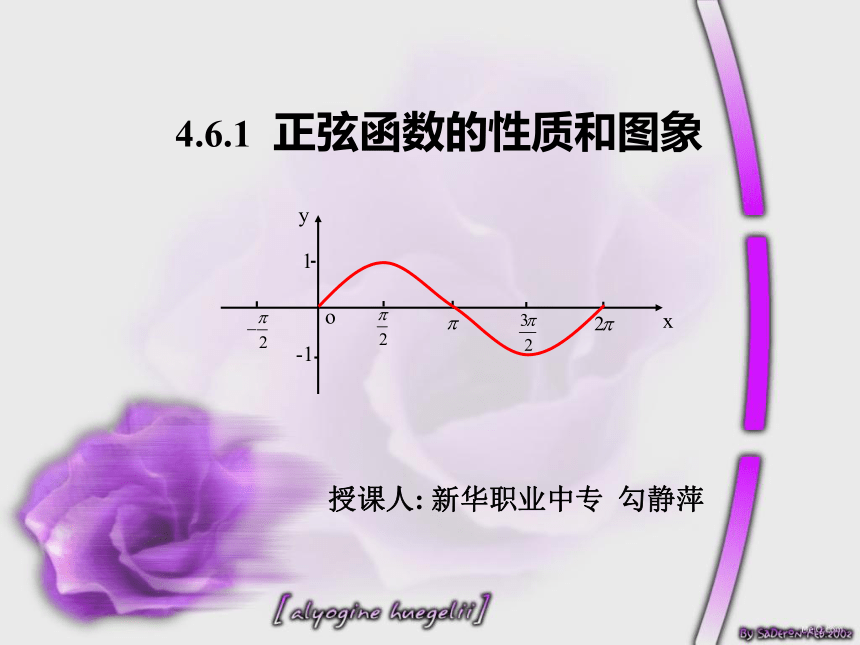
4.6.1 正弦函数的性质和图象
y
x
o
1
-1
授课人: 新华职业中专 勾静萍
知识应用
知识探索：正弦的性质
知识回顾
图象与画法
学习目标
学习目标
1、通过分析正弦函数的性质，画出图象。
2、理解正弦函数的定义域、奇偶性、单调性、
周期性，并会简单的应用，解决相关问题。
3、会用“五点法”画正弦函数的图象。
知识回顾
前几节课我们学习了三角函数的概念及诱导
公式。下面请同学回忆一下：
1、三角函数的几何意义。
2、角α+2kπ与角α的终边有什么关系。
3、关于-α与α的诱导公式。
想一想：怎样画出正弦函数f(x)=sinx的图象 ？
正弦函数的性质
分析：
由诱导公式（1）：sin（x+2π）= sinx
sin ( x-2π）= sinx
自变量x每增加或减少2π，正弦函数值不变。
周期性：
我们把2π称为f(x)=sinx的一个“周期”
想一想：自变量x每增加或减少多少，正弦函数值不变？
正弦函数的性质
奇偶性 ：
分析：
由诱导公式（4）得:
f(x)=sinx在（-∞，+∞）是 ________
奇函数
正弦函数的性质
P(x,y)
1
1
y
x
o
设角 的终边与单位圆交于p(x,y),则sin =y
从0逐渐增大到1
从1逐渐减小到0
f(x)=sin(x) 在 上是
在 上是
增函数
减函数
当 从0逐渐增大到 ,sin
当 从 逐渐增大到 ,sin
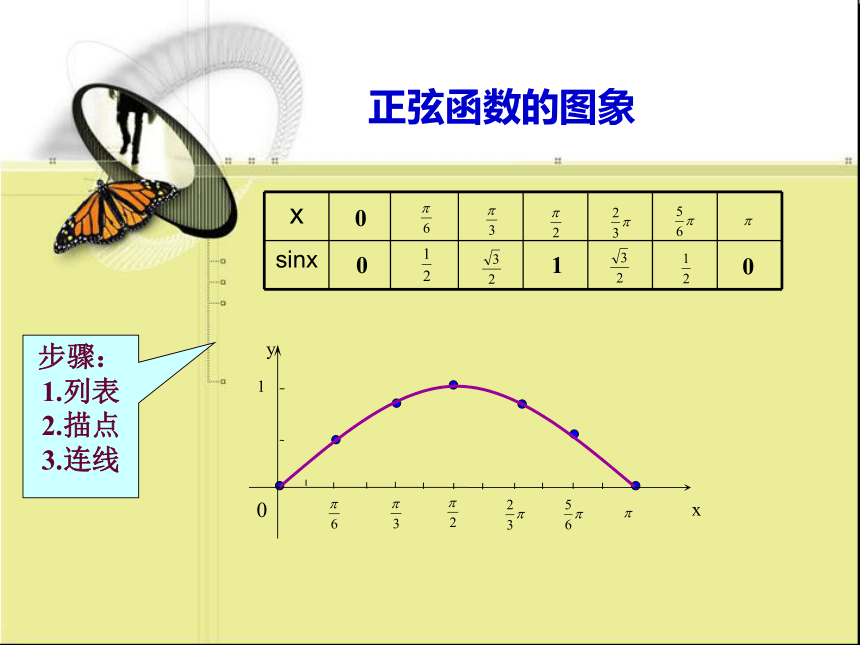
正弦函数的图象
由以上的性质可知：
要画 的图象
只要先画 y=sinx 在 _______ 的图象
周期性
只要先画 y=sinx 在 _______ 的图象
奇偶性
正弦函数的图象
步骤：
1.列表
2.描点
3.连线
x
sinx
0
1
0
0
y
x
1
0
o
x
y
1
正弦函数的图象
y=sinx x [0, ]
y=sinx x [-π,π]
o
y
1
x
6
-1
-
2
3
4
5
-2
-3
-4

y=sinx x [-π,π]
y=sinx x (-∞，+∞)
正弦曲线
一）正弦函数f(x)=sinx的主要性质：
评注：
R
[-1，1]
2π
奇函数
原点对称
6）、在 处达到__________，在 处达到
______________(k∈z)
1）、 定义域是________；
2）、值域是_________；
3）、最小正周期是_________；
4）、在（-∞，+∞）上是__________，图象关于____________；
5）、在 上是_________，在
上是__________。
增函数
减函数
最大值1
最小值-1
评注：
二）、一般地，对于定义域为A的y=f(x),如果存在一
个常数T≠0，使得对于每一个x∈A,都有x±T∈A，且
f(x+T)=f(x)
则把T叫做函数f(x)的一个周期，称y=f(x)是周期函数。
如果在所有的正周期中，存在一个最小的数，则把它称
为f(x)的“最小正周期”。
五点法——
(0,0)
( ,1)
( ,0)
( ,-1)
( 2 ,0)
y
x
o
1
-1
如何作出正弦函数的图象（在精确度要求不太高时）？
(0,0)
( ,1)
( ,0)
( ,-1)
( 2 ,0)
(0,0)
( ,1)
( ,0)
( ,1)
( 2 ,0)
(0,0)
( ,1)
( ,0)
( ,1)
( 2 ,0)
(0,0)
( ,1)
( ,0)
( ,1)
( 2 ,0)
(0,0)
( ,1)
( ,0)
( ,1)
( 2 ,0)
(0,0)
( ,1)
( ,0)
( ,-1)
( 2 ,0)
(0,0)
( ,1)
( ,0)
( ,-1)
( 2 ,0)
(0,0)
( ,1)
( ,0)
( ,-1)
( 2 ,0)
评注：
例题分析
例1、利用“五点法”作函数y=1+sinx在
上的图像。
x 0
sinx
1+sinx
例2 、 求函数 在x取何值时到达
最大值？在x取何值是到达最小值？
关键点：把 看作一个整体。
解； 在 处到达最大值1。
即，当 时， 达到最大值1。
在 处达到最小值-1。
即，当 时， 达到最小值-1。
例3 、 比较下列各组正弦值的大小：
分析： 利用正弦函数的不同区间上的单调性进行比较。
解： 1）因为
并且f(x)=sinx在 上是增函数，所以
2）因为
并且f(x)=sinx在 上是减函数，所以
练习
1、比较下列各组正弦值的大小：
2、利用“五点法”作函数y=2sinx在
上的图像。
1. 正弦曲线——五点作图法
2.正弦函数的6个性质。
y
x
o
1
-1
y=sinx，x [0, 2 ]
课堂小结
课后作业：
课本（必作）
P149 A组
2、3、 5、（1）
思考题：如何得到余弦函数的图象及性质。