其他版 高中二年级 直线与平面垂直的判定
文档属性
| 名称 | 其他版 高中二年级 直线与平面垂直的判定 |

|
|
| 格式 | zip | ||
| 文件大小 | 279.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-10 07:36:44 | ||
图片预览

文档简介
(共22张PPT)
直线与平面垂直的判定
直线与平面
垂直的判定
定义
定理
例题
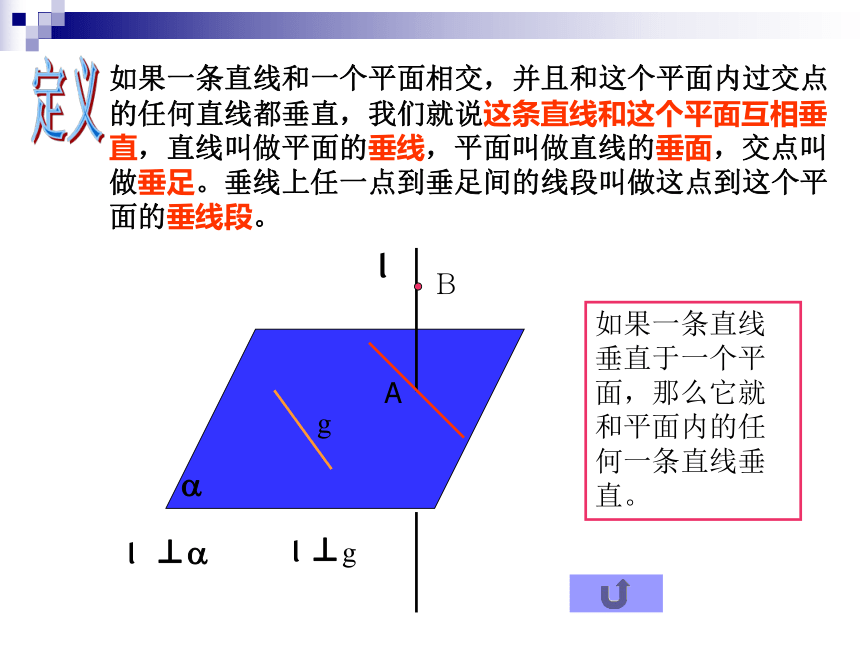
如果一条直线和一个平面相交,并且和这个平面内过交点的任何直线都垂直,我们就说这条直线和这个平面互相垂直,直线叫做平面的垂线,平面叫做直线的垂面,交点叫做垂足。垂线上任一点到垂足间的线段叫做这点到这个平面的垂线段。
如果一条直线垂直于一个平面,那么它就和平面内的任何一条直线垂直。
a
l
l ⊥a
g
l ⊥g
A
B
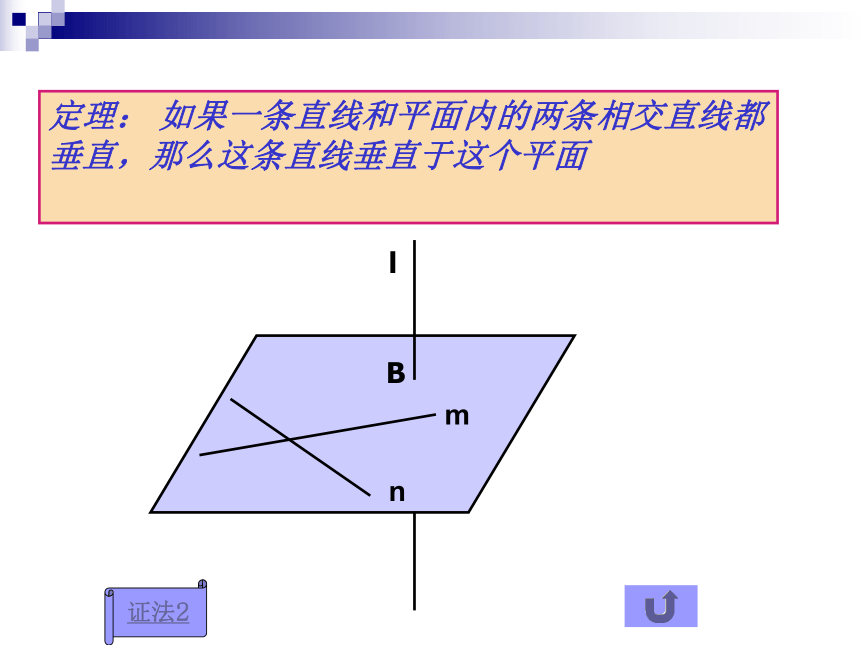
定理: 如果一条直线和平面内的两条相交直线都垂直,那么这条直线垂直于这个平面
m
n
l
B
证法2
a
l
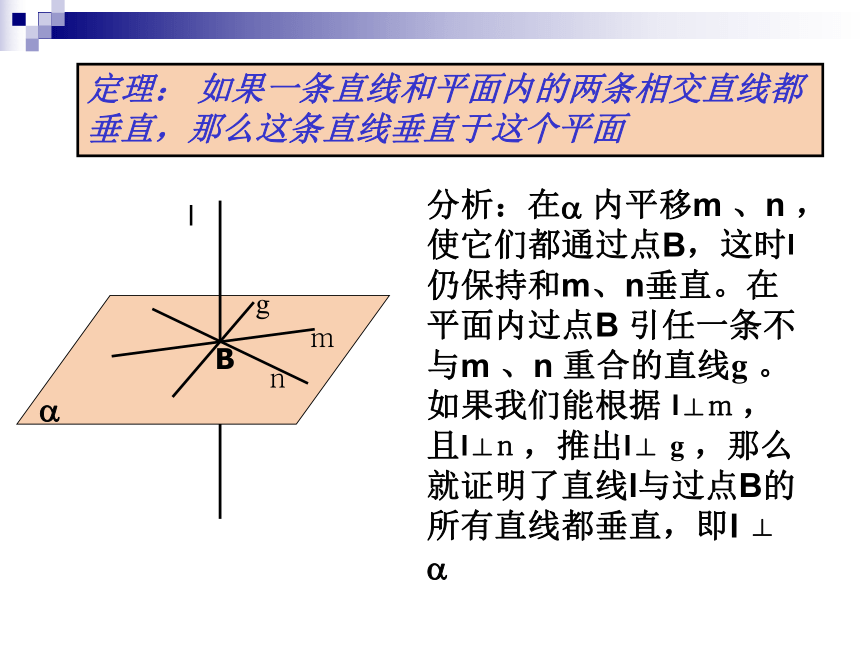
定理: 如果一条直线和平面内的两条相交直线都垂直,那么这条直线垂直于这个平面
B
g
m
n
分析:在a 内平移m 、n ,使它们都通过点B,这时l仍保持和m、n垂直。在平面内过点B 引任一条不与m 、n 重合的直线g 。如果我们能根据 l⊥m ,且l⊥n ,推出l⊥ g ,那么就证明了直线l与过点B的所有直线都垂直,即l ⊥ a
a
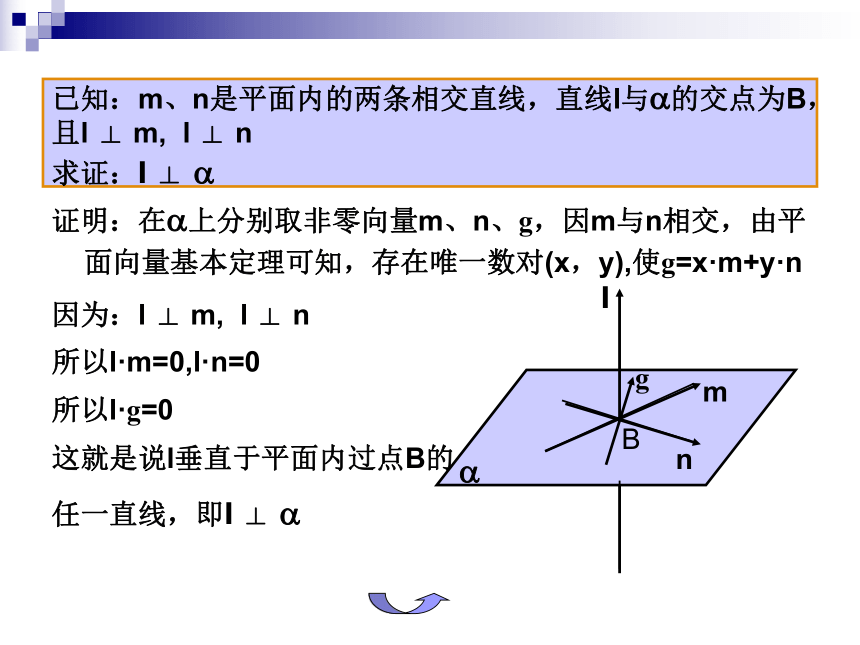
已知:m、n是平面内的两条相交直线,直线l与a的交点为B,且l ⊥ m, l ⊥ n
求证:l ⊥ a
证明:在a上分别取非零向量m、n、g,因m与n相交,由平面向量基本定理可知,存在唯一数对(x,y),使g=x·m+y·n
因为:l ⊥ m, l ⊥ n
所以l·m=0,l·n=0
所以l·g=0
这就是说l垂直于平面内过点B的
任一直线,即l ⊥ a
m
n
g
l
B
B
A
A’
m
n
g
c
D
E
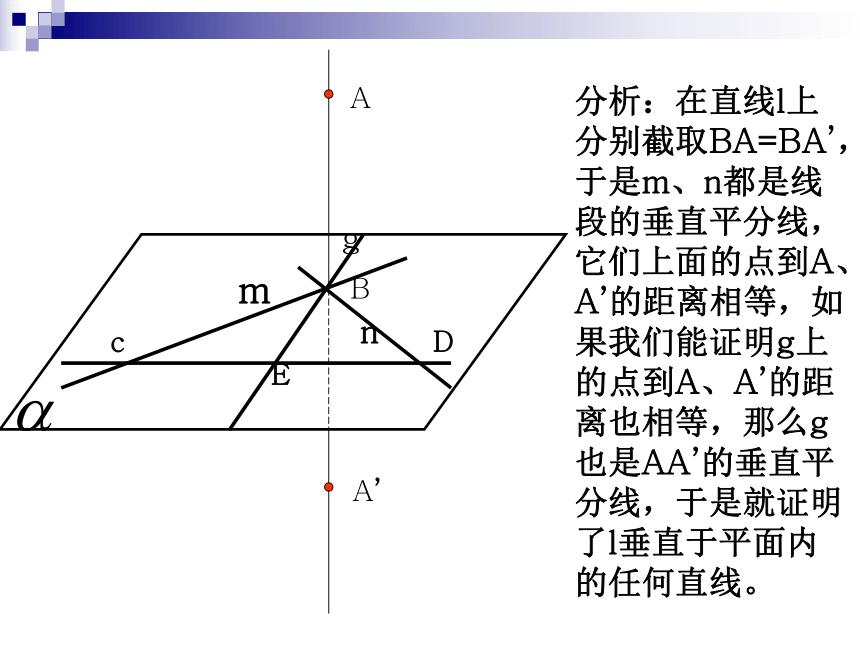
分析:在直线l上 分别截取BA=BA’,于是m、n都是线段的垂直平分线,它们上面的点到A、A’的距离相等,如果我们能证明g上的点到A、A’的距离也相等,那么g也是AA’的垂直平分线,于是就证明了l垂直于平面内的任何直线。
B
A
A’
m
n
g
C
D
E
证明:在g上任取一
点E,过点E在α内
引不通过点B的直
线,分别与m、n相
交于点C、D。连结
AC、A’C、AD、
A’D、AE、A’E。
则有AC=A’C,
AD=A’D。
B
A
A’
m
n
g
C
D
E
证明:在g上任取一点E,过点E在α内引不通过点B的直线,分别与m、n相交于点C、D。连结AC、A’C、AD、A’D、AE、A’E。则有AC=A’C,AD=A’D。所以△ACD≌△A’CD。所以∠ACE=∠A’CE。所以△ACE≌△A’CE。于是,得EA=EA’,所以g是AA’的垂直平分线。所以l⊥g。
B
m
n
g
C
D
E
A
A’
证明:在g上任取一点E,过点E在α内引不通过点B的直线,分别与m、n相交于点C、D。连结AC、A’C、AD、A’D、AE、A’E。则有AC=A’C,AD=A’D。所以△ACD≌△A’CD。所以∠ACE=∠A’CE。所以△ACE≌△A’CE。于是,得EA=EA’,所以g是AA’的垂直平分线。所以l⊥g。
A
A’
B
m
n
g
C
D
E
A
A’
证明:在g上任取一点E,过点E在α内引不通过点B的直线,分别与m、n相交于点C、D。连结AC、A’C、AD、A’D、AE、A’E。则有AC=A’C,AD=A’D。所以△ACD≌△A’CD。所以∠ACE=∠A’CE。所以△ACE≌△A’CE。于是,得EA=EA’,所以g是AA’的垂直平分线。所以l⊥g。
A
A’
E
例1 已知长方体ABCD—A’B’C’D’。求与直线AA’垂直平面
问:1、与直线AB垂直的平面 2、与直线B’C’垂直的平面
B’
C’
A
B
D
A’
D’
C
平 面 A DD ’A ’和 平 面 B C’ C ’B
平面DCC’D’和平面ABB’A’
答案1
答案2
例2 有一旗杆高8米,它的顶端A挂一条长为10米的绳子,拉紧绳子并把它的下端分别放在地面α上的两点C、D(和旗杆脚不在同一直线上)。如果这两点和旗杆脚B的距离都是6米.
求证:旗杆和地面垂直。
证明:在△ABC和△ABD中,因为AB=8m,BC=BD=6m,AC=AD=10m,所以AB2+BC2=62+82=102=AC2,AB2+BD2=62+82=102=AD2。所以∠ABC=∠ABD=900,即AB⊥BC,AB⊥BD。又知B、C、D三点不共线,所以AB⊥平面BCD。这就表明了旗杆和地面垂直。
A
B
D
C
返回3
(1)线面垂直的定义
(2)线面垂直的判定
垂直平面内两相交 直线
拿一张矩形的纸对折后略微展开,竖立在桌面上,说明折痕为什么和桌面垂直.
如果一条直线垂直于一个平面内的:
(1)三角形的两条边
(2)梯形的两条边
(3)圆的两条直径
试问这条直线是否与平面垂直
直线与平面垂直的判定
直线与平面
垂直的判定
定义
定理
例题
如果一条直线和一个平面相交,并且和这个平面内过交点的任何直线都垂直,我们就说这条直线和这个平面互相垂直,直线叫做平面的垂线,平面叫做直线的垂面,交点叫做垂足。垂线上任一点到垂足间的线段叫做这点到这个平面的垂线段。
如果一条直线垂直于一个平面,那么它就和平面内的任何一条直线垂直。
a
l
l ⊥a
g
l ⊥g
A
B
定理: 如果一条直线和平面内的两条相交直线都垂直,那么这条直线垂直于这个平面
m
n
l
B
证法2
a
l
定理: 如果一条直线和平面内的两条相交直线都垂直,那么这条直线垂直于这个平面
B
g
m
n
分析:在a 内平移m 、n ,使它们都通过点B,这时l仍保持和m、n垂直。在平面内过点B 引任一条不与m 、n 重合的直线g 。如果我们能根据 l⊥m ,且l⊥n ,推出l⊥ g ,那么就证明了直线l与过点B的所有直线都垂直,即l ⊥ a
a
已知:m、n是平面内的两条相交直线,直线l与a的交点为B,且l ⊥ m, l ⊥ n
求证:l ⊥ a
证明:在a上分别取非零向量m、n、g,因m与n相交,由平面向量基本定理可知,存在唯一数对(x,y),使g=x·m+y·n
因为:l ⊥ m, l ⊥ n
所以l·m=0,l·n=0
所以l·g=0
这就是说l垂直于平面内过点B的
任一直线,即l ⊥ a
m
n
g
l
B
B
A
A’
m
n
g
c
D
E
分析:在直线l上 分别截取BA=BA’,于是m、n都是线段的垂直平分线,它们上面的点到A、A’的距离相等,如果我们能证明g上的点到A、A’的距离也相等,那么g也是AA’的垂直平分线,于是就证明了l垂直于平面内的任何直线。
B
A
A’
m
n
g
C
D
E
证明:在g上任取一
点E,过点E在α内
引不通过点B的直
线,分别与m、n相
交于点C、D。连结
AC、A’C、AD、
A’D、AE、A’E。
则有AC=A’C,
AD=A’D。
B
A
A’
m
n
g
C
D
E
证明:在g上任取一点E,过点E在α内引不通过点B的直线,分别与m、n相交于点C、D。连结AC、A’C、AD、A’D、AE、A’E。则有AC=A’C,AD=A’D。所以△ACD≌△A’CD。所以∠ACE=∠A’CE。所以△ACE≌△A’CE。于是,得EA=EA’,所以g是AA’的垂直平分线。所以l⊥g。
B
m
n
g
C
D
E
A
A’
证明:在g上任取一点E,过点E在α内引不通过点B的直线,分别与m、n相交于点C、D。连结AC、A’C、AD、A’D、AE、A’E。则有AC=A’C,AD=A’D。所以△ACD≌△A’CD。所以∠ACE=∠A’CE。所以△ACE≌△A’CE。于是,得EA=EA’,所以g是AA’的垂直平分线。所以l⊥g。
A
A’
B
m
n
g
C
D
E
A
A’
证明:在g上任取一点E,过点E在α内引不通过点B的直线,分别与m、n相交于点C、D。连结AC、A’C、AD、A’D、AE、A’E。则有AC=A’C,AD=A’D。所以△ACD≌△A’CD。所以∠ACE=∠A’CE。所以△ACE≌△A’CE。于是,得EA=EA’,所以g是AA’的垂直平分线。所以l⊥g。
A
A’
E
例1 已知长方体ABCD—A’B’C’D’。求与直线AA’垂直平面
问:1、与直线AB垂直的平面 2、与直线B’C’垂直的平面
B’
C’
A
B
D
A’
D’
C
平 面 A DD ’A ’和 平 面 B C’ C ’B
平面DCC’D’和平面ABB’A’
答案1
答案2
例2 有一旗杆高8米,它的顶端A挂一条长为10米的绳子,拉紧绳子并把它的下端分别放在地面α上的两点C、D(和旗杆脚不在同一直线上)。如果这两点和旗杆脚B的距离都是6米.
求证:旗杆和地面垂直。
证明:在△ABC和△ABD中,因为AB=8m,BC=BD=6m,AC=AD=10m,所以AB2+BC2=62+82=102=AC2,AB2+BD2=62+82=102=AD2。所以∠ABC=∠ABD=900,即AB⊥BC,AB⊥BD。又知B、C、D三点不共线,所以AB⊥平面BCD。这就表明了旗杆和地面垂直。
A
B
D
C
返回3
(1)线面垂直的定义
(2)线面垂直的判定
垂直平面内两相交 直线
拿一张矩形的纸对折后略微展开,竖立在桌面上,说明折痕为什么和桌面垂直.
如果一条直线垂直于一个平面内的:
(1)三角形的两条边
(2)梯形的两条边
(3)圆的两条直径
试问这条直线是否与平面垂直
同课章节目录
