广东省韶关市2012届高三第一次调研考试数学(理)试题
文档属性
| 名称 | 广东省韶关市2012届高三第一次调研考试数学(理)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 408.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-10 00:00:00 | ||
图片预览




文档简介
2012届高三调研考试数学试题(理科)
本卷分选择题非选择题两部分,共4页,满分150分.考试用时间120分钟.
注意事项:
考生务必将自己的姓名、班级、学校用蓝、黑墨水钢笔签字笔写在答题卷上;
选择题、填空题每小题得出答案后,请将答案填写在答题卷相应指定位置上。答在试题卷上不得分;
3.考试结束,考生只需将答题卷交回.
4. 参考公式:
锥体的体积公式,其中是锥体的底面积,是锥体的高.
一、选择题(本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若集合是函数的定义域,是函数的定义域,则等于( )
A. B. C. D.
2.在复平面内,复数对应的点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.下列命题正确的是( )
A. B.
C.是的充分不必要条件 D.若,则
4.为了在一条河上建一座桥,施工前在河两岸打上两个桥位桩(如图),要测算两点的距离,测量人员在岸边定出基线,测得,,就可以计算出两点的距离为( )
A. B.
C. D.
5.已知等比数列中,各项都是正数,且成等差数列,则等于( )
A. B. C. D.
6.执行如图的程序框图,那么输出的值是( )
A. B. C.1 D.2
7.平面向量与的夹角为,,,
则( )
A. B. C. D.
8.设函数的定义域为,若存在非零实数满足,均有,且,则称为上的高调函数.如果定义域为的函数是奇函数,当时,,且为上的高调函数,那么实数的取值范围是( )
A. B. C. D.
二.填空题:本大题共7小题,每小题5分,满分30分.
(一)必做题:第9、10、11、12、13题为必做题,每道试题考生都必须作答.
9. 展开式中含项的系数为 .
10. 某班50名学生在一次百米测试中,成绩全部介于13秒与18秒
之间,将测试结果分成五组:每一组;第二组,…,
第五组.右图是按上述分组方法得到的频率分布直方图
若成绩大于或等于14秒且小于16秒认为良好,则该班在这次百
米测试中成绩良好的人数是__________.
11. 已知的椭圆的两个焦点,若椭圆上一点满足,则椭圆的离心率
12.如图是边长为的为正方形的对角线,将绕
直线旋转一周后形成的几何体的体积等于
13.在平面中的角的内角平分线分面积所成的比, 将这个结论类比到空间:在三棱锥中,平面平分二面角且与交于, 则类比的结论为______________.
(二)选做题:第14、15题为选做题,考生只能选做一题,两题全答的,只计算前一题的得分.
14.(坐标系与参数方程选做题)
极坐标系中,圆:,则圆心到直线的距离是 .
15.(几何证明选讲选做题)
已知圆的半径为,从圆外一点引切线和割线,
圆心到的距离为,,则切线的长为
____________.
三、解答题: 本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)
已知函数的最小正周期为.
(1)求的值;
(2)求函数的单调递增区间及其图象的对称轴方程。
17.(本小题满分12分)
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜爱打篮球 不喜爱打篮球 合计
男生 5
女生 10
合计 50
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为.
(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为,求的分布列与期望.
下面的临界值表供参考:
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
(参考公式:,其中)
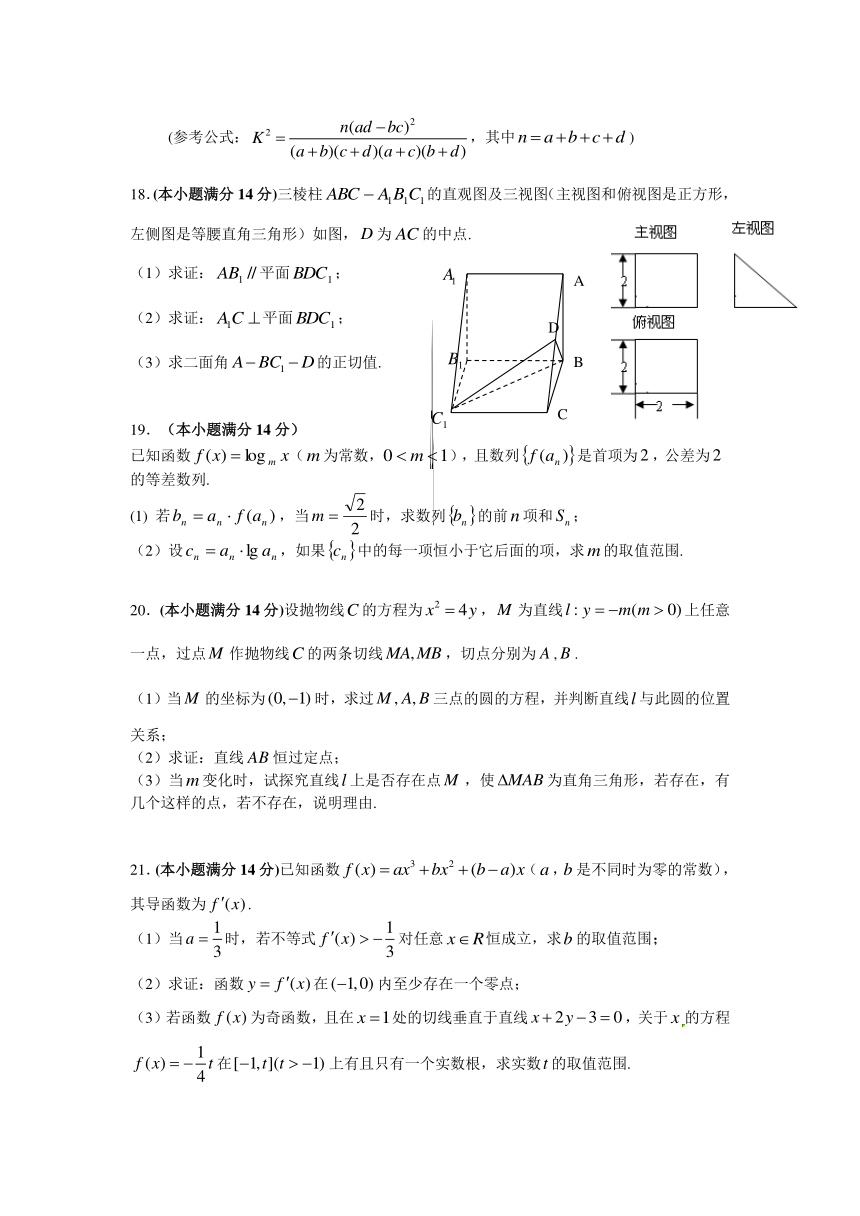
18.(本小题满分14分)三棱柱的直观图及三视图(主视图和俯视图是正方形,左侧图是等腰直角三角形)如图,为的中点.
(1)求证:平面;
(2)求证:平面;
(3)求二面角的正切值.
19.(本小题满分14分)
已知函数(为常数,),且数列是首项为,公差为的等差数列.
(1) 若,当时,求数列的前项和;
(2)设,如果中的每一项恒小于它后面的项,求的取值范围.
20.(本小题满分14分)设抛物线的方程为,为直线上任意一点,过点作抛物线的两条切线,切点分别为,.
(1)当的坐标为时,求过三点的圆的方程,并判断直线与此圆的位置关系;
(2)求证:直线恒过定点;
(3)当变化时,试探究直线上是否存在点,使为直角三角形,若存在,有几个这样的点,若不存在,说明理由.
21.(本小题满分14分)已知函数(,是不同时为零的常数),其导函数为.
(1)当时,若不等式对任意恒成立,求的取值范围;
(2)求证:函数在内至少存在一个零点;
(3)若函数为奇函数,且在处的切线垂直于直线,关于的方程在上有且只有一个实数根,求实数的取值范围.
2012年韶关市高三年级调研考试
数学(理科)参考答案和评分标准
一、选择题:
二、填空题:
9.1, 10. , 11. , 12. , 13. , 14. ,
15.
三、解答题:
16.(本小题满分12分)
解:(1) ……………………2分
=, ……………………3分
因为最小正周期为,所以,解得, ………………4分
所以, ……………… 5分
所以. ……………6分
(2)由,
可得, ……………8分
所以,函数的单调递增区间为 …………9分
由得.
所以,图象的对称轴方程为. …………………12分
17.(本小题满分12分)
解:(1) 列联表补充如下:----------------------------------------3分
喜爱打篮球 不喜爱打篮球 合计
男生 20 5 25
女生 10 15 25
合计 30 20 50
(2)∵------------------------5分
∴在犯错误的概率不超过0.005的前提下,认为喜爱打篮球与性别有关.---------------------6分
(3)喜爱打篮球的女生人数的可能取值为.-------------------------7分
其概率分别为,,
--------------------------10分
故的分布列为:
--------------------------11分
的期望值为: ---------------------12分
18.解:由三视图可知,几何体为直三棱柱—,侧面
为边长为2的正方形,底面是等腰直角三角形,………2分(1)连BC交于O,连接OD,在中,O,D分别是,
AC的中点,
而平面,平面,平面………………..4分
(2)直三棱柱—中,平面,平面,
,,D为AC的中点,,
平面,①………………..6分
又,
在正方形②………………..8分
由①②,又,
……………………………………………………………9
(3)解法一;提示:所求二面角与二面角C--D互余……………………………………..12
取BC中点H,有DH⊥平面,过H作垂线,垂足为E,
所以二面角C--D的平面角是∠DEH…………….. ……………………12分
,因为二面角A--D与二面角C--D互余,所以二面角A--D的正切值为;……………..14
解法二(补形)如图补成正方体,易得∠O1OS为二面角的平面角,
……………..14
解法三(空间向量法)以为原点建系,易得
设平面D的法向量由
得令得…………..12
又平面A的法向量
设二面角A--D的平面角为
所以…………..14
19. (本小题满分14分)
(1) 证:由题意,即, ……1分
. ……2分
,
当时,. …………3分
∴, ①
② ……4分
①-②,得
……6分
∴. ……7分
(2) 解:由(Ⅰ)知,,要使对一切成立,
即对一切成立. ……8分
,对一切恒成立,
只需,……10分
单调递增,∴当时,. ……12分
∴,且, ∴. ……13分
综上所述,存在实数满足条件. ……14分
20.(本小题满分14分)
解:(1)当的坐标为时,设过点的切线方程为,代入,整理得,
令,解得,
代入方程得,故得, .................2分
因为到的中点的距离为,
从而过三点的圆的方程为.
易知此圆与直线相切. ..................4分
(2)证法一:设切点分别为,,过抛物线上点的切线方程为,代入,整理得
,又因为,所以................5分
从而过抛物线上点的切线方程为即
又切线过点,所以得 ① 即
同理可得过点的切线为,
又切线过点,所以得 ② 即.................6分
即点,均满足即,故直线的方程为 .................7分
又为直线上任意一点,故对任意成立,所以,从而直线恒过定点 ..................8分
证法二:设过的抛物线的切线方程为,代入,消去,得
即:.................5分
从而,此时,
所以切点的坐标分别为,.................6分
因为,,
,
所以的中点坐标为
故直线的方程为,即...............7分
又为直线上任意一点,故对任意成立,所以,从而直线恒过定点 ..................8分
证法三:由已知得,求导得,切点分别为,,故过点的切线斜率为,从而切线方程为即
又切线过点,所以得 ① 即
同理可得过点的切线为,
又切线过点,所以得 ②
即.................6分
即点,均满足即,故直线的方程为 .................7分
又为直线上任意一点,故对任意成立,所以,从而直线恒过定点 ..................8分
(3)解法一:由(2)中①②两式知是方程的两实根,故有
(*)
将,,代入上(*)式得
∴
, .................9分
①当时,,直线上任意一点均有,为直角三角形; .................10分
②当时,,,不可能为直角三角形;
.................11分
③当时,,.
因为,,
所以
若,则,整理得,
又因为,所以,
因为方程有解的充要条件是.
所以当时,有或,为直角三角形..............13分
综上所述,当时,直线上任意一点,使为直角三角形,当时,直线上存在两点,使为直角三角形;当或时,不是直角三角形.
.................14分
解法二:由(2)知,且是方程的两实根,即,从而,
所以
当时,即时,直线上任意一点均有,为直角三角形; .................10分
当时,即时,与不垂直。
因为,,
所以
若,则,整理得,
又因为,所以,
因为方程有解的充要条件是.
所以当时,有或,为直角三角形..............13分
综上所述,当时,直线上任意一点,使为直角三角形,当时,直线上存在两点,使为直角三角形;当或时,不是直角三角形.
.................14分
21.(本小题满分14分)
解析:(1)
解:解:(1)当时,,………1分
依题意 即恒成立
,解得
所以b的取值范围是…………………………………4分
(2)证明:因为,
解法一:当时,符合题意. ……………………………5分
当时,,令,则,
令,, 当时,,
在内有零点;……………………………7分
当时,,
在内有零点.
当时,在内至少有一个零点.
综上可知,函数在内至少有一个零点. ……………………………9分
解法二:,,
.
因为a,b不同时为零,所以,故结论成立.
(3)因为为奇函数,所以,所以,.
又在处的切线垂直于直线,所以,即.
……………………………………………………………………………………10分
在,上是单调递增函数,在上是单调递减函数,由解得,,
法一:如图所示,作与的图像,若只有一个交点,则
①当时,,
即,解得;
②当时,,
解得;
③当时,显示不成立;
④当时,,
即,解得;
⑤当时,,
解得;
⑥当时,.
………………………………………………………………13分
综上t的取值范围是或或.………………14分
法二:由,.
作与的图知交点横坐标为,
当时,过图象上任意一点向左作平行于轴的直线与都只有唯一交点,当取其它任何值时都有两个或没有交点。
所以当时,方程在上有且只有一个实数根.
2012届高三调研考试理科数学答题卡
一.选择题答卷:
题号 1 2 3 4 5 6 7 8
答案
二、填空题答卷:
9.________________________. 10.__________________________.
11.________________________. 12.__________________________.
13.______________________ 14._____________________
15._____________________
解答题共80分
16.(本题满分12分)
17.(本题满分12分)
喜爱打篮球 不喜爱打篮球 合计
男生 5
女生 10
合计 50
18. (本题满分14分)
19. (本题满分14分)
20.(本题满分14分)
21. (本题满分14分)
B
A
C
开始
否
是
输出
结束
A
B
C
D
(第15小题)
A
B
C
D
EMBED Equation.DSMT4 EMBED Equation.DSMT4 EMBED Equation.DSMT4
A
B
C
D
O
A
B
C
D
H
E
A
C
D
O
S
B
1
O
-1
y
x
x
y
-1
x
y
O
O
①
-1
t
②
-1
t
x
④
y
t
x
O
y
y
O
EMBED Equation.DSMT4
t
x
2
2
主视图
左视图
俯视图
2
A
B
C
D
EMBED Equation.DSMT4 EMBED Equation.DSMT4 EMBED Equation.DSMT4
本卷分选择题非选择题两部分,共4页,满分150分.考试用时间120分钟.
注意事项:
考生务必将自己的姓名、班级、学校用蓝、黑墨水钢笔签字笔写在答题卷上;
选择题、填空题每小题得出答案后,请将答案填写在答题卷相应指定位置上。答在试题卷上不得分;
3.考试结束,考生只需将答题卷交回.
4. 参考公式:
锥体的体积公式,其中是锥体的底面积,是锥体的高.
一、选择题(本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若集合是函数的定义域,是函数的定义域,则等于( )
A. B. C. D.
2.在复平面内,复数对应的点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.下列命题正确的是( )
A. B.
C.是的充分不必要条件 D.若,则
4.为了在一条河上建一座桥,施工前在河两岸打上两个桥位桩(如图),要测算两点的距离,测量人员在岸边定出基线,测得,,就可以计算出两点的距离为( )
A. B.
C. D.
5.已知等比数列中,各项都是正数,且成等差数列,则等于( )
A. B. C. D.
6.执行如图的程序框图,那么输出的值是( )
A. B. C.1 D.2
7.平面向量与的夹角为,,,
则( )
A. B. C. D.
8.设函数的定义域为,若存在非零实数满足,均有,且,则称为上的高调函数.如果定义域为的函数是奇函数,当时,,且为上的高调函数,那么实数的取值范围是( )
A. B. C. D.
二.填空题:本大题共7小题,每小题5分,满分30分.
(一)必做题:第9、10、11、12、13题为必做题,每道试题考生都必须作答.
9. 展开式中含项的系数为 .
10. 某班50名学生在一次百米测试中,成绩全部介于13秒与18秒
之间,将测试结果分成五组:每一组;第二组,…,
第五组.右图是按上述分组方法得到的频率分布直方图
若成绩大于或等于14秒且小于16秒认为良好,则该班在这次百
米测试中成绩良好的人数是__________.
11. 已知的椭圆的两个焦点,若椭圆上一点满足,则椭圆的离心率
12.如图是边长为的为正方形的对角线,将绕
直线旋转一周后形成的几何体的体积等于
13.在平面中的角的内角平分线分面积所成的比, 将这个结论类比到空间:在三棱锥中,平面平分二面角且与交于, 则类比的结论为______________.
(二)选做题:第14、15题为选做题,考生只能选做一题,两题全答的,只计算前一题的得分.
14.(坐标系与参数方程选做题)
极坐标系中,圆:,则圆心到直线的距离是 .
15.(几何证明选讲选做题)
已知圆的半径为,从圆外一点引切线和割线,
圆心到的距离为,,则切线的长为
____________.
三、解答题: 本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)
已知函数的最小正周期为.
(1)求的值;
(2)求函数的单调递增区间及其图象的对称轴方程。
17.(本小题满分12分)
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜爱打篮球 不喜爱打篮球 合计
男生 5
女生 10
合计 50
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为.
(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为,求的分布列与期望.
下面的临界值表供参考:
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
(参考公式:,其中)
18.(本小题满分14分)三棱柱的直观图及三视图(主视图和俯视图是正方形,左侧图是等腰直角三角形)如图,为的中点.
(1)求证:平面;
(2)求证:平面;
(3)求二面角的正切值.
19.(本小题满分14分)
已知函数(为常数,),且数列是首项为,公差为的等差数列.
(1) 若,当时,求数列的前项和;
(2)设,如果中的每一项恒小于它后面的项,求的取值范围.
20.(本小题满分14分)设抛物线的方程为,为直线上任意一点,过点作抛物线的两条切线,切点分别为,.
(1)当的坐标为时,求过三点的圆的方程,并判断直线与此圆的位置关系;
(2)求证:直线恒过定点;
(3)当变化时,试探究直线上是否存在点,使为直角三角形,若存在,有几个这样的点,若不存在,说明理由.
21.(本小题满分14分)已知函数(,是不同时为零的常数),其导函数为.
(1)当时,若不等式对任意恒成立,求的取值范围;
(2)求证:函数在内至少存在一个零点;
(3)若函数为奇函数,且在处的切线垂直于直线,关于的方程在上有且只有一个实数根,求实数的取值范围.
2012年韶关市高三年级调研考试
数学(理科)参考答案和评分标准
一、选择题:
二、填空题:
9.1, 10. , 11. , 12. , 13. , 14. ,
15.
三、解答题:
16.(本小题满分12分)
解:(1) ……………………2分
=, ……………………3分
因为最小正周期为,所以,解得, ………………4分
所以, ……………… 5分
所以. ……………6分
(2)由,
可得, ……………8分
所以,函数的单调递增区间为 …………9分
由得.
所以,图象的对称轴方程为. …………………12分
17.(本小题满分12分)
解:(1) 列联表补充如下:----------------------------------------3分
喜爱打篮球 不喜爱打篮球 合计
男生 20 5 25
女生 10 15 25
合计 30 20 50
(2)∵------------------------5分
∴在犯错误的概率不超过0.005的前提下,认为喜爱打篮球与性别有关.---------------------6分
(3)喜爱打篮球的女生人数的可能取值为.-------------------------7分
其概率分别为,,
--------------------------10分
故的分布列为:
--------------------------11分
的期望值为: ---------------------12分
18.解:由三视图可知,几何体为直三棱柱—,侧面
为边长为2的正方形,底面是等腰直角三角形,………2分(1)连BC交于O,连接OD,在中,O,D分别是,
AC的中点,
而平面,平面,平面………………..4分
(2)直三棱柱—中,平面,平面,
,,D为AC的中点,,
平面,①………………..6分
又,
在正方形②………………..8分
由①②,又,
……………………………………………………………9
(3)解法一;提示:所求二面角与二面角C--D互余……………………………………..12
取BC中点H,有DH⊥平面,过H作垂线,垂足为E,
所以二面角C--D的平面角是∠DEH…………….. ……………………12分
,因为二面角A--D与二面角C--D互余,所以二面角A--D的正切值为;……………..14
解法二(补形)如图补成正方体,易得∠O1OS为二面角的平面角,
……………..14
解法三(空间向量法)以为原点建系,易得
设平面D的法向量由
得令得…………..12
又平面A的法向量
设二面角A--D的平面角为
所以…………..14
19. (本小题满分14分)
(1) 证:由题意,即, ……1分
. ……2分
,
当时,. …………3分
∴, ①
② ……4分
①-②,得
……6分
∴. ……7分
(2) 解:由(Ⅰ)知,,要使对一切成立,
即对一切成立. ……8分
,对一切恒成立,
只需,……10分
单调递增,∴当时,. ……12分
∴,且, ∴. ……13分
综上所述,存在实数满足条件. ……14分
20.(本小题满分14分)
解:(1)当的坐标为时,设过点的切线方程为,代入,整理得,
令,解得,
代入方程得,故得, .................2分
因为到的中点的距离为,
从而过三点的圆的方程为.
易知此圆与直线相切. ..................4分
(2)证法一:设切点分别为,,过抛物线上点的切线方程为,代入,整理得
,又因为,所以................5分
从而过抛物线上点的切线方程为即
又切线过点,所以得 ① 即
同理可得过点的切线为,
又切线过点,所以得 ② 即.................6分
即点,均满足即,故直线的方程为 .................7分
又为直线上任意一点,故对任意成立,所以,从而直线恒过定点 ..................8分
证法二:设过的抛物线的切线方程为,代入,消去,得
即:.................5分
从而,此时,
所以切点的坐标分别为,.................6分
因为,,
,
所以的中点坐标为
故直线的方程为,即...............7分
又为直线上任意一点,故对任意成立,所以,从而直线恒过定点 ..................8分
证法三:由已知得,求导得,切点分别为,,故过点的切线斜率为,从而切线方程为即
又切线过点,所以得 ① 即
同理可得过点的切线为,
又切线过点,所以得 ②
即.................6分
即点,均满足即,故直线的方程为 .................7分
又为直线上任意一点,故对任意成立,所以,从而直线恒过定点 ..................8分
(3)解法一:由(2)中①②两式知是方程的两实根,故有
(*)
将,,代入上(*)式得
∴
, .................9分
①当时,,直线上任意一点均有,为直角三角形; .................10分
②当时,,,不可能为直角三角形;
.................11分
③当时,,.
因为,,
所以
若,则,整理得,
又因为,所以,
因为方程有解的充要条件是.
所以当时,有或,为直角三角形..............13分
综上所述,当时,直线上任意一点,使为直角三角形,当时,直线上存在两点,使为直角三角形;当或时,不是直角三角形.
.................14分
解法二:由(2)知,且是方程的两实根,即,从而,
所以
当时,即时,直线上任意一点均有,为直角三角形; .................10分
当时,即时,与不垂直。
因为,,
所以
若,则,整理得,
又因为,所以,
因为方程有解的充要条件是.
所以当时,有或,为直角三角形..............13分
综上所述,当时,直线上任意一点,使为直角三角形,当时,直线上存在两点,使为直角三角形;当或时,不是直角三角形.
.................14分
21.(本小题满分14分)
解析:(1)
解:解:(1)当时,,………1分
依题意 即恒成立
,解得
所以b的取值范围是…………………………………4分
(2)证明:因为,
解法一:当时,符合题意. ……………………………5分
当时,,令,则,
令,, 当时,,
在内有零点;……………………………7分
当时,,
在内有零点.
当时,在内至少有一个零点.
综上可知,函数在内至少有一个零点. ……………………………9分
解法二:,,
.
因为a,b不同时为零,所以,故结论成立.
(3)因为为奇函数,所以,所以,.
又在处的切线垂直于直线,所以,即.
……………………………………………………………………………………10分
在,上是单调递增函数,在上是单调递减函数,由解得,,
法一:如图所示,作与的图像,若只有一个交点,则
①当时,,
即,解得;
②当时,,
解得;
③当时,显示不成立;
④当时,,
即,解得;
⑤当时,,
解得;
⑥当时,.
………………………………………………………………13分
综上t的取值范围是或或.………………14分
法二:由,.
作与的图知交点横坐标为,
当时,过图象上任意一点向左作平行于轴的直线与都只有唯一交点,当取其它任何值时都有两个或没有交点。
所以当时,方程在上有且只有一个实数根.
2012届高三调研考试理科数学答题卡
一.选择题答卷:
题号 1 2 3 4 5 6 7 8
答案
二、填空题答卷:
9.________________________. 10.__________________________.
11.________________________. 12.__________________________.
13.______________________ 14._____________________
15._____________________
解答题共80分
16.(本题满分12分)
17.(本题满分12分)
喜爱打篮球 不喜爱打篮球 合计
男生 5
女生 10
合计 50
18. (本题满分14分)
19. (本题满分14分)
20.(本题满分14分)
21. (本题满分14分)
B
A
C
开始
否
是
输出
结束
A
B
C
D
(第15小题)
A
B
C
D
EMBED Equation.DSMT4 EMBED Equation.DSMT4 EMBED Equation.DSMT4
A
B
C
D
O
A
B
C
D
H
E
A
C
D
O
S
B
1
O
-1
y
x
x
y
-1
x
y
O
O
①
-1
t
②
-1
t
x
④
y
t
x
O
y
y
O
EMBED Equation.DSMT4
t
x
2
2
主视图
左视图
俯视图
2
A
B
C
D
EMBED Equation.DSMT4 EMBED Equation.DSMT4 EMBED Equation.DSMT4
同课章节目录
