第10章 5.带电粒子在电场中的运动 Word版含解析
文档属性
| 名称 | 第10章 5.带电粒子在电场中的运动 Word版含解析 |

|
|
| 格式 | docx | ||
| 文件大小 | 289.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-05-05 00:00:00 | ||
图片预览


文档简介
5.带电粒子在电场中的运动
1.如图所示,两平行金属板竖直放置,板上A、B两孔正好水平相对,板间电压为500 V。一个动能为400 eV的电子从A孔沿垂直金属板方向射入电场中,经过一段时间电子离开电场,若不考虑重力的影响,则电子离开电场时的动能大小为( )
A.900 eV B.500 eV
C.400 eV D.-100 eV
答案:C
解析:电子从A向B运动时,电场力对电子做负功,若电子到达B时,克服电场力所做的功W=qU=500eV>400eV,因此电子不能到达B,电子向右做减速运动,在到达B之前速度变为零,然后反向运动,从A点离开电场,在整个过程中,电场力做功为零,由动能定理可知,电子离开电场时的动能Ek=400eV,故C正确。
2.一束正离子以相同的速率从同一位置,沿垂直于电场方向飞入匀强电场中,所有离子的运动轨迹都是一样的,这说明所有粒子( )
A.都具有相同的质量
B.都具有相同的电荷量
C.具有相同的比荷
D.都是同一元素的同位素
答案:C
解析:由偏转距离y=12qEmlv02=qEl22mv02可知,若运动轨迹相同,则水平位移相同,偏转距离y也应相同,已知E、l、v0是相同的,所以应有qm相同。
3.如图所示,一个平行板电容器充电后与电源断开,从负极板处自由释放一个电子(不计重力),设其到达正极板时的速度为v1,加速度为a1。若将两极板间的距离增大为原来的2倍,再从负极板处自由释放一个电子,设其到达正极板时的速度为v2,加速度为a2,则( )
A.a1∶a2=1∶1,v1∶v2=1∶2
B.a1∶a2=2∶1,v1∶v2=1∶2
C.a1∶a2=2∶1,v1∶v2=2∶1
D.a1∶a2=1∶1,v1∶v2=1∶2
答案:D
解析:电容器充电后与电源断开,再增大两极板间的距离时,电场强度不变,电子在电场中受到的电场力不变,故a1∶a2=1∶1。由动能定理Ue=12mv2得v=2Uem,因两极板间的距离增大为原来的2倍,由U=Ed知,电势差U增大为原来的2倍,故v1∶v2=1∶2。
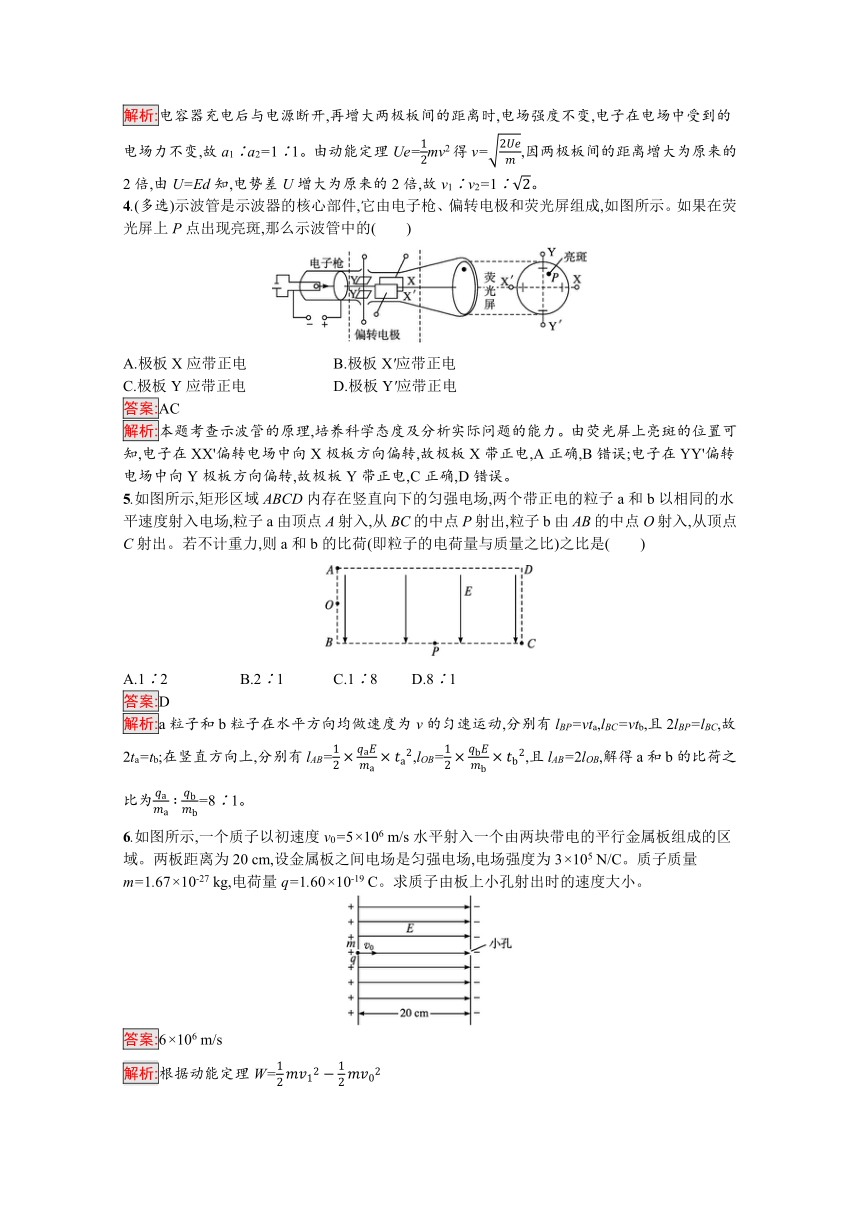
4.(多选)示波管是示波器的核心部件,它由电子枪、偏转电极和荧光屏组成,如图所示。如果在荧光屏上P点出现亮斑,那么示波管中的( )
A.极板X应带正电 B.极板X'应带正电
C.极板Y应带正电 D.极板Y'应带正电
答案:AC
解析:本题考查示波管的原理,培养科学态度及分析实际问题的能力。由荧光屏上亮斑的位置可知,电子在XX'偏转电场中向X极板方向偏转,故极板X带正电,A正确,B错误;电子在YY'偏转电场中向Y极板方向偏转,故极板Y带正电,C正确,D错误。
5.如图所示,矩形区域ABCD内存在竖直向下的匀强电场,两个带正电的粒子a和b以相同的水平速度射入电场,粒子a由顶点A射入,从BC的中点P射出,粒子b由AB的中点O射入,从顶点C射出。若不计重力,则a和b的比荷(即粒子的电荷量与质量之比)之比是( )
A.1∶2 B.2∶1 C.1∶8 D.8∶1
答案:D
解析:a粒子和b粒子在水平方向均做速度为v的匀速运动,分别有lBP=vta,lBC=vtb,且2lBP=lBC,故2ta=tb;在竖直方向上,分别有lAB=12×qaEma×ta2,lOB=12×qbEmb×tb2,且lAB=2lOB,解得a和b的比荷之比为qama∶qbmb=8∶1。
6.如图所示,一个质子以初速度v0=5×106 m/s水平射入一个由两块带电的平行金属板组成的区域。两板距离为20 cm,设金属板之间电场是匀强电场,电场强度为3×105 N/C。质子质量m=1.67×10-27 kg,电荷量q=1.60×10-19 C。求质子由板上小孔射出时的速度大小。
答案:6×106 m/s
解析:根据动能定理W=12mv12-12mv02
而W=Ep1-Ep0=qEd=1.60×10-19×3×105×0.2J=9.6×10-15J
所以v1=2Wm+v02=2×9.6×10-151.67×10-27+(5×106)2m/s≈6×106m/s
质子飞出时的速度约为6×106m/s。
7.如图所示,喷墨打印机中的墨滴在进入偏转电场之前会被带上一定量的电荷,在电场的作用下使电荷发生偏转到达纸上。已知两偏转极板长度l=1.5×10-2 m,两极板间电场强度E=1.2×106 N/C,墨滴的质量m=1.0×10-13 kg,电荷量q=1.0×10-16 C,墨滴在进入电场前的速度v0=15 m/s,方向与两极板平行。不计空气阻力和墨滴重力,假设偏转电场只局限在平行极板内部,忽略边缘电场的影响。
(1)判断墨滴带正电荷还是负电荷。
(2)求墨滴在两极板之间运动的时间。
(3)求墨滴离开电场时在竖直方向上的位移y。
答案:(1)负电荷
(2)1.0×10-3 s
(3)6.0×10-4 m
解析:(2)墨滴在水平方向做匀速直线运动,那么墨滴在两板之间运动的时间t=lv0
代入数据可得t=1.0×10-3s。
(3)墨滴在竖直方向做初速度为零的匀加速直线运动,加速度
a=Eqm
代入数据可得a=1.2×103m/s2
离开偏转板时在竖直方向的位移y=12at2
代入数据可得y=6.0×10-4m。
选考奠基 素养提升
1.如图所示,从F处释放一个无初速度的电子(重力不计)向B板方向运动,下列说法错误的是(设电源电动势为U)( )
A.电子到达B板时的动能是Ue
B.电子从B板到达C板动能变化量为零
C.电子到达D板时动能是3Ue
D.电子在A板和D板之间做往复运动
答案:C
解析:电子在AB之间做匀加速运动,且eU=ΔEk,选项A正确;电子在BC之间做匀速运动,选项B正确;在CD之间做匀减速运动,到达D板时,速度减为零,选项C错误,选项D正确。
2.如图所示,电子在电势差为U1的加速电场中由静止开始运动,然后射入电势差为U2的两块平行极板间的电场中,射入方向跟极板平行,整个装置处在真空中,重力可忽略,在满足电子能射出平行板区的条件下,下述四种情况中,一定能使电子的偏转角θ变大的是( )
A.U1变大、U2变大 B.U1变小、U2变大
C.U1变大、U2变小 D.U1变小、U2变小
答案:B
解析:设电子被加速后获得的速度为v0,则由动能定理得qU1=12mv02
设极板长为l,则电子在电场中偏转所用的时间为t=lv0
设电子在平行板间受静电力作用产生的加速度为a,由牛顿第二定律得a=qEm=qU2dm
电子射出偏转电场时,平行于电场方向的速度为vy=at
解得vy=qU2ldmv0
故tanθ=vyv0=qU2ldmv02=qU2l2dqU1=U2l2dU1
所以U2变大或U1变小都可能使偏转角θ变大,故选项B正确。
3.在光滑水平面上有一比荷qm=1.0×10-7 C/kg的带正电小球,静止在O点,以O点为原点,在水平面内建立坐标系Oxy,现突然加一沿x轴正方向、电场强度为2.0×106 V/m的匀强电场,小球开始运动。经过1 s,所加电场突然变为沿y轴正方向,电场强度大小不变。则小球运动的轨迹和位置坐标正确的是( )
答案:C
解析:本题考查带电小球的偏转问题,通过分析与计算,培养科学思维能力。
小球加速度大小a=qEm=0.20m/s2,1s末小球速度vx=at=0.20m/s,沿x轴方向距离x1=12at2=12×0.20×12m=0.10m。第2s内小球做类平抛运动,轨迹为抛物线,x方向x2=vxt=0.20m,沿y轴方向y2=12at2=12×0.20×12m=0.1m,故第2s末小球坐标为(0.30m,0.10m),故C正确。
4.(多选)如图所示,一电子沿x轴正方向射入匀强电场,在电场中的运动轨迹为OCD,已知lOA=lAB,电子过C、D两点时竖直方向的分速度为vCy和vDy;电子在OC段和OD段动能的变化量分别为ΔEk1和ΔEk2,则( )
A.vCy∶vDy=1∶2
B.vCy∶vDy=1∶4
C.ΔEk1∶ΔEk2=1∶3
D.ΔEk1∶ΔEk2=1∶4
答案:AD
解析:电子沿Ox轴射入匀强电场,做类平抛运动,水平方向做匀速直线运动,已知lOA=lAB,则电子从O到C与从C到D的时间相等。电子在竖直方向上做初速度为零的匀加速运动,则有vCy=atOC,vDy=atOD,所以vCy∶vDy=tOC∶tOD=1∶2,故A正确,B错误。根据匀变速直线运动的推论可知,在竖直方向上,yOC∶yOD=1∶4,根据动能定理得ΔEk1=qEyOC,ΔEk2=qEyOD,则得,ΔEk1∶ΔEk2=1∶4,故C错误,D正确。
5.长为l的平行金属板水平放置,两极板带等量的异种电荷,板间形成匀强电场,一个电荷量为+q、质量为m的带电粒子,以初速度v0紧贴上极板垂直于电场线方向进入该电场,刚好从下极板边缘射出,射出时速度恰与下极板成30°角,如图所示,不计粒子重力,求:
(1)粒子末速度的大小;
(2)匀强电场的电场强度;
(3)两极板间的距离。
答案:(1)23v03 (2)3mv023ql (3)36l
解析:(1)粒子离开电场时,合速度与水平方向夹角为30°,由几何关系得合速度
v=v0cos30°=23v03。
(2)粒子在匀强电场中做类平抛运动,
在水平方向上,l=v0t,在竖直方向上,vy=at,
vy=v0tan30°=3v03,
由牛顿第二定律得,qE=ma,解得,E=3mv023ql。
(3)粒子做类平抛运动,
在竖直方向上,d=12at2,解得d=36l。
6.如图所示,AMB是一条长l=10 m的绝缘水平轨道,固定在离水平地面高h=1.25 m处,A、B为端点,M为中点。轨道MB处在方向竖直向上、大小E=5×103 N/C的匀强电场中。一质量m=0.1 kg、电荷量q=+1.3×10-4 C的可视为质点的滑块以初速度v0=6 m/s在轨道上自A点开始向右运动,经M点进入电场,从B点离开电场。已知滑块与轨道间的动摩擦因数μ=0.2,g取10 m/s2,求:
(1)滑块到达M点时的速度大小;
(2)滑块从M点运动到B点所用的时间。
答案:(1)4 m/s
(2)107s
解析:(1)滑块在AM段的加速度大小为
a1=Ffm=μmgm=2m/s2
由运动学公式得vM2-v02=2(-a1)l2
代入数据解得vM=4m/s。
(2)滑块在MB段的加速度大小为
a2=μ(mg-qE)m=0.7m/s2,
由运动学公式得l2=vMt-12a2t2,且t≤vMa2=407s,
代入数据解得t=107s。
1.如图所示,两平行金属板竖直放置,板上A、B两孔正好水平相对,板间电压为500 V。一个动能为400 eV的电子从A孔沿垂直金属板方向射入电场中,经过一段时间电子离开电场,若不考虑重力的影响,则电子离开电场时的动能大小为( )
A.900 eV B.500 eV
C.400 eV D.-100 eV
答案:C
解析:电子从A向B运动时,电场力对电子做负功,若电子到达B时,克服电场力所做的功W=qU=500eV>400eV,因此电子不能到达B,电子向右做减速运动,在到达B之前速度变为零,然后反向运动,从A点离开电场,在整个过程中,电场力做功为零,由动能定理可知,电子离开电场时的动能Ek=400eV,故C正确。
2.一束正离子以相同的速率从同一位置,沿垂直于电场方向飞入匀强电场中,所有离子的运动轨迹都是一样的,这说明所有粒子( )
A.都具有相同的质量
B.都具有相同的电荷量
C.具有相同的比荷
D.都是同一元素的同位素
答案:C
解析:由偏转距离y=12qEmlv02=qEl22mv02可知,若运动轨迹相同,则水平位移相同,偏转距离y也应相同,已知E、l、v0是相同的,所以应有qm相同。
3.如图所示,一个平行板电容器充电后与电源断开,从负极板处自由释放一个电子(不计重力),设其到达正极板时的速度为v1,加速度为a1。若将两极板间的距离增大为原来的2倍,再从负极板处自由释放一个电子,设其到达正极板时的速度为v2,加速度为a2,则( )
A.a1∶a2=1∶1,v1∶v2=1∶2
B.a1∶a2=2∶1,v1∶v2=1∶2
C.a1∶a2=2∶1,v1∶v2=2∶1
D.a1∶a2=1∶1,v1∶v2=1∶2
答案:D
解析:电容器充电后与电源断开,再增大两极板间的距离时,电场强度不变,电子在电场中受到的电场力不变,故a1∶a2=1∶1。由动能定理Ue=12mv2得v=2Uem,因两极板间的距离增大为原来的2倍,由U=Ed知,电势差U增大为原来的2倍,故v1∶v2=1∶2。
4.(多选)示波管是示波器的核心部件,它由电子枪、偏转电极和荧光屏组成,如图所示。如果在荧光屏上P点出现亮斑,那么示波管中的( )
A.极板X应带正电 B.极板X'应带正电
C.极板Y应带正电 D.极板Y'应带正电
答案:AC
解析:本题考查示波管的原理,培养科学态度及分析实际问题的能力。由荧光屏上亮斑的位置可知,电子在XX'偏转电场中向X极板方向偏转,故极板X带正电,A正确,B错误;电子在YY'偏转电场中向Y极板方向偏转,故极板Y带正电,C正确,D错误。
5.如图所示,矩形区域ABCD内存在竖直向下的匀强电场,两个带正电的粒子a和b以相同的水平速度射入电场,粒子a由顶点A射入,从BC的中点P射出,粒子b由AB的中点O射入,从顶点C射出。若不计重力,则a和b的比荷(即粒子的电荷量与质量之比)之比是( )
A.1∶2 B.2∶1 C.1∶8 D.8∶1
答案:D
解析:a粒子和b粒子在水平方向均做速度为v的匀速运动,分别有lBP=vta,lBC=vtb,且2lBP=lBC,故2ta=tb;在竖直方向上,分别有lAB=12×qaEma×ta2,lOB=12×qbEmb×tb2,且lAB=2lOB,解得a和b的比荷之比为qama∶qbmb=8∶1。
6.如图所示,一个质子以初速度v0=5×106 m/s水平射入一个由两块带电的平行金属板组成的区域。两板距离为20 cm,设金属板之间电场是匀强电场,电场强度为3×105 N/C。质子质量m=1.67×10-27 kg,电荷量q=1.60×10-19 C。求质子由板上小孔射出时的速度大小。
答案:6×106 m/s
解析:根据动能定理W=12mv12-12mv02
而W=Ep1-Ep0=qEd=1.60×10-19×3×105×0.2J=9.6×10-15J
所以v1=2Wm+v02=2×9.6×10-151.67×10-27+(5×106)2m/s≈6×106m/s
质子飞出时的速度约为6×106m/s。
7.如图所示,喷墨打印机中的墨滴在进入偏转电场之前会被带上一定量的电荷,在电场的作用下使电荷发生偏转到达纸上。已知两偏转极板长度l=1.5×10-2 m,两极板间电场强度E=1.2×106 N/C,墨滴的质量m=1.0×10-13 kg,电荷量q=1.0×10-16 C,墨滴在进入电场前的速度v0=15 m/s,方向与两极板平行。不计空气阻力和墨滴重力,假设偏转电场只局限在平行极板内部,忽略边缘电场的影响。
(1)判断墨滴带正电荷还是负电荷。
(2)求墨滴在两极板之间运动的时间。
(3)求墨滴离开电场时在竖直方向上的位移y。
答案:(1)负电荷
(2)1.0×10-3 s
(3)6.0×10-4 m
解析:(2)墨滴在水平方向做匀速直线运动,那么墨滴在两板之间运动的时间t=lv0
代入数据可得t=1.0×10-3s。
(3)墨滴在竖直方向做初速度为零的匀加速直线运动,加速度
a=Eqm
代入数据可得a=1.2×103m/s2
离开偏转板时在竖直方向的位移y=12at2
代入数据可得y=6.0×10-4m。
选考奠基 素养提升
1.如图所示,从F处释放一个无初速度的电子(重力不计)向B板方向运动,下列说法错误的是(设电源电动势为U)( )
A.电子到达B板时的动能是Ue
B.电子从B板到达C板动能变化量为零
C.电子到达D板时动能是3Ue
D.电子在A板和D板之间做往复运动
答案:C
解析:电子在AB之间做匀加速运动,且eU=ΔEk,选项A正确;电子在BC之间做匀速运动,选项B正确;在CD之间做匀减速运动,到达D板时,速度减为零,选项C错误,选项D正确。
2.如图所示,电子在电势差为U1的加速电场中由静止开始运动,然后射入电势差为U2的两块平行极板间的电场中,射入方向跟极板平行,整个装置处在真空中,重力可忽略,在满足电子能射出平行板区的条件下,下述四种情况中,一定能使电子的偏转角θ变大的是( )
A.U1变大、U2变大 B.U1变小、U2变大
C.U1变大、U2变小 D.U1变小、U2变小
答案:B
解析:设电子被加速后获得的速度为v0,则由动能定理得qU1=12mv02
设极板长为l,则电子在电场中偏转所用的时间为t=lv0
设电子在平行板间受静电力作用产生的加速度为a,由牛顿第二定律得a=qEm=qU2dm
电子射出偏转电场时,平行于电场方向的速度为vy=at
解得vy=qU2ldmv0
故tanθ=vyv0=qU2ldmv02=qU2l2dqU1=U2l2dU1
所以U2变大或U1变小都可能使偏转角θ变大,故选项B正确。
3.在光滑水平面上有一比荷qm=1.0×10-7 C/kg的带正电小球,静止在O点,以O点为原点,在水平面内建立坐标系Oxy,现突然加一沿x轴正方向、电场强度为2.0×106 V/m的匀强电场,小球开始运动。经过1 s,所加电场突然变为沿y轴正方向,电场强度大小不变。则小球运动的轨迹和位置坐标正确的是( )
答案:C
解析:本题考查带电小球的偏转问题,通过分析与计算,培养科学思维能力。
小球加速度大小a=qEm=0.20m/s2,1s末小球速度vx=at=0.20m/s,沿x轴方向距离x1=12at2=12×0.20×12m=0.10m。第2s内小球做类平抛运动,轨迹为抛物线,x方向x2=vxt=0.20m,沿y轴方向y2=12at2=12×0.20×12m=0.1m,故第2s末小球坐标为(0.30m,0.10m),故C正确。
4.(多选)如图所示,一电子沿x轴正方向射入匀强电场,在电场中的运动轨迹为OCD,已知lOA=lAB,电子过C、D两点时竖直方向的分速度为vCy和vDy;电子在OC段和OD段动能的变化量分别为ΔEk1和ΔEk2,则( )
A.vCy∶vDy=1∶2
B.vCy∶vDy=1∶4
C.ΔEk1∶ΔEk2=1∶3
D.ΔEk1∶ΔEk2=1∶4
答案:AD
解析:电子沿Ox轴射入匀强电场,做类平抛运动,水平方向做匀速直线运动,已知lOA=lAB,则电子从O到C与从C到D的时间相等。电子在竖直方向上做初速度为零的匀加速运动,则有vCy=atOC,vDy=atOD,所以vCy∶vDy=tOC∶tOD=1∶2,故A正确,B错误。根据匀变速直线运动的推论可知,在竖直方向上,yOC∶yOD=1∶4,根据动能定理得ΔEk1=qEyOC,ΔEk2=qEyOD,则得,ΔEk1∶ΔEk2=1∶4,故C错误,D正确。
5.长为l的平行金属板水平放置,两极板带等量的异种电荷,板间形成匀强电场,一个电荷量为+q、质量为m的带电粒子,以初速度v0紧贴上极板垂直于电场线方向进入该电场,刚好从下极板边缘射出,射出时速度恰与下极板成30°角,如图所示,不计粒子重力,求:
(1)粒子末速度的大小;
(2)匀强电场的电场强度;
(3)两极板间的距离。
答案:(1)23v03 (2)3mv023ql (3)36l
解析:(1)粒子离开电场时,合速度与水平方向夹角为30°,由几何关系得合速度
v=v0cos30°=23v03。
(2)粒子在匀强电场中做类平抛运动,
在水平方向上,l=v0t,在竖直方向上,vy=at,
vy=v0tan30°=3v03,
由牛顿第二定律得,qE=ma,解得,E=3mv023ql。
(3)粒子做类平抛运动,
在竖直方向上,d=12at2,解得d=36l。
6.如图所示,AMB是一条长l=10 m的绝缘水平轨道,固定在离水平地面高h=1.25 m处,A、B为端点,M为中点。轨道MB处在方向竖直向上、大小E=5×103 N/C的匀强电场中。一质量m=0.1 kg、电荷量q=+1.3×10-4 C的可视为质点的滑块以初速度v0=6 m/s在轨道上自A点开始向右运动,经M点进入电场,从B点离开电场。已知滑块与轨道间的动摩擦因数μ=0.2,g取10 m/s2,求:
(1)滑块到达M点时的速度大小;
(2)滑块从M点运动到B点所用的时间。
答案:(1)4 m/s
(2)107s
解析:(1)滑块在AM段的加速度大小为
a1=Ffm=μmgm=2m/s2
由运动学公式得vM2-v02=2(-a1)l2
代入数据解得vM=4m/s。
(2)滑块在MB段的加速度大小为
a2=μ(mg-qE)m=0.7m/s2,
由运动学公式得l2=vMt-12a2t2,且t≤vMa2=407s,
代入数据解得t=107s。
同课章节目录
- 第九章 静电场及其应用
- 1 电荷
- 2 库仑定律
- 3 电场 电场强度
- 4 静电的防止与利用
- 第十章 静电场中的能量
- 1 电势能和电势
- 2 电势差
- 3 电势差与电场强度的关系
- 4 电容器的电容
- 5 带电粒子在电场中的运动
- 第十一章 电路及其应用
- 1 电源和电流
- 2 导体的电阻
- 3 实验:导体电阻率的测量
- 4 串联电路和并联电路
- 5 实验:练习使用多用电表
- 第十二章 电能 能量守恒定律
- 1 电路中的能量转化
- 2 闭合电路的欧姆定律
- 3 实验:电池电动势和内阻的测量
- 4 能源与可持续发展
- 第十三章 电磁感应与电磁波初步
- 1 磁场 磁感线
- 2 磁感应强度 磁通量
- 3 电磁感应现象及应用
- 4 电磁波的发现及应用
- 5 能量量子化
