8.1-1功 课件 23张PPT
文档属性
| 名称 | 8.1-1功 课件 23张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 555.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-05-05 13:57:18 | ||
图片预览








文档简介
第八章 第1节 功与功率
第1课时 功
问题导入
起重机竖直提升重物时,重物运动的方向与力的方向一致,则力对物体做的功为力的大小与重物移动距离的乘积。更普遍的情形是物体运动的方向与力的方向不一致,例如马拉雪橇时拉力方向和雪橇运动方向间有一个角度。这时应当怎样计算功呢?
知识梳理
一、功基本概念
1. 概念:一个物体受到力的作用,并在力的方向上发生了一段位移,这个力就对物体做了功。
?
?
?
?
2. 公式:W=Flcosα
(1)α是力与位移方向之间的夹角, l为物体在力作用下发生的位移;
(2)该公式一般用于求恒力做功。
3. 单位:焦(耳) 符号: J
(单位制换算: 1J=1N·m=1kg·m/s2·m=1kg·m2/s2)
?
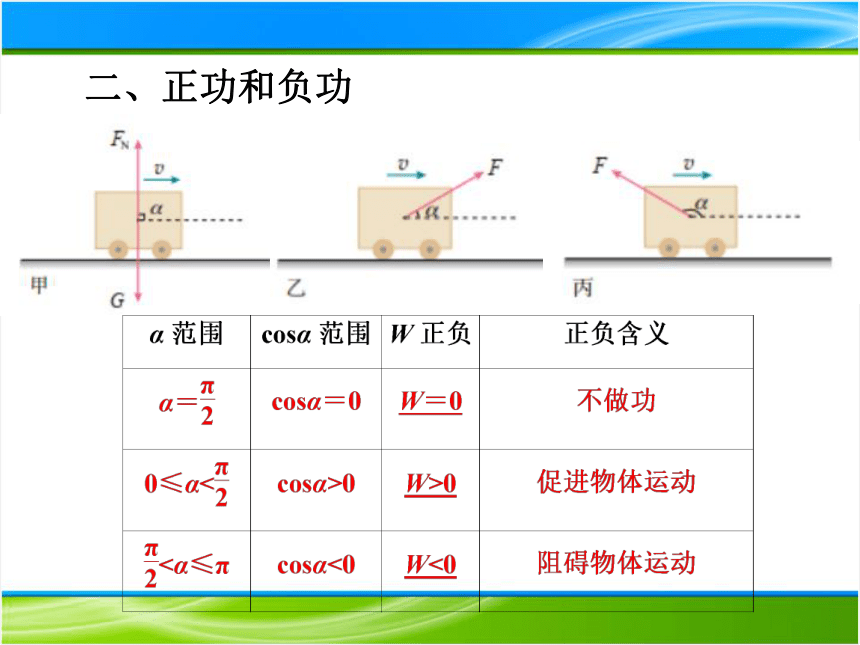
二、正功和负功
二、正功和负功
1.矢标性:功是标量 ,正负号不表示大小,也不表示方向,表示对物体运动的促进或阻碍。
2.说明:某力做-5J功,可以说物体克服该力做了5J功
三、总功的计算
1.各个力分别对物体所做功的代数和。
公式:W合=WF1+WF2+…+WFn
2.几个力的合力对物体所做的功。
公式:W合=F合lcosα
(α为F合与位移l的夹角,F合为恒力)
二、行星运动的近似处理
行星的轨道与圆十分接近,在中学阶段的研究中我们按圆轨道处理,即:
1. 行星绕太阳运动的轨道十分接近圆,太阳处在圆心.
2.对某一行星来说,它绕太阳做圆周运动的角速度(或线速度大小)不变,即行星做匀速圆周运动.
3.所有行星轨道半径的三次方跟它的公转
周期的二次方的比值都相等,表达式为
判一判
(1)有力作用在物体上,并且物体也发生了位移时,力对物体一定做了功. (×)
(2)力对物体不做功,说明物体的位移一定为零. (×)
(3)力F1做功10 J,F2做功-15 J,力F1比F2做功少. (√)
重点突破
[例1](多选)一同学穿着旱冰鞋处于静止状态,推竖直墙壁后有了向后的速度,关于该同学推墙壁的过程,下列说法正确的是( )
A. 墙壁对该同学做正功
B. 墙壁对该同学没有做功
C. 该同学对墙壁做正功
D. 该同学对墙壁没有做功
任务一:对功的理解
答案:BD
答案: ABD
[变式训练1-1](多选)如图所示,物体静止在斜面上,现使物体随着斜面一起向右匀速运动,通过一段位移s,则( )
A. 静摩擦力对物体做了正功
B. 支持力对物体做了负功
C. 重力对物体做了正功
D. 合外力对物体做功为零
答案: D
[变式训练1-2]下列关于做功的说法正确的是 ( )
A. 凡是受力作用的物体,一定有力对物体做功
B. 凡是发生了位移的物体,一定有力对物体做功
C. 只要物体受力的同时又有位移发生,则一定有力对物体做功
D. 只要物体受力,又在力的方向上发生了位移,则一定有力对物体做功
[例2]如图所示,平行于斜面向上的拉力F使质量为m的物体匀速地沿着长为L,倾角为α的斜面的一端向上滑到另一端,物体与斜面间的动摩擦因数为μ,分别求作用在物体上各力对物体所做的功.
任务二:功的计算
[变式训练2-1] 一个质量m=2 kg的物体,受到与水平方向成37°角斜向上方的力F=10 N作用,在水平地面上移动的距离l=2 m,物体与地面间的滑动摩擦力Ff=4.2 N,求外力对物体所做的总功.(cos37°=0.8,sin37°=0.6)
解法一:
W1=Flcos37°=10×2×0.8 J=16 J
W2=Fflcos180°=-4.2×2 J=-8.4 J
W=W1+W2=7.6 J
解法二:
F合=Fcos37°-Ff=10×0.8 N-4.2 N=3.8 N
W=F合l=3.8×2 J=7.6 J.
[变式训练2-2]当上题中的拉力F= 100/3N时,物体刚好与地面接触且无压力,求物体在该力作用下从静止开始运动2 s过程中合力做的功.
1.功的计算
(1)计算功时首先应明确要求的是哪一个力的功,物体所受的各个力做功时互不影响。
(2)两种方法求总功:①W总=F合lcosα (几个力同时作用,均为恒力,一般做匀变速直线运动)
②W总=W1+W2+…+Wn (任何情况都可适用)
总结反思
巩固训练
1.在光滑水平面上推物块和在粗糙水平面上推物块相比较,如果所用的水平推力相同,物块在推力作用下通过的位移相同,则推力对物块所做的功( )
A.一样大
B.在光滑水平面上推力所做的功较多
C.在粗糙水平面上推力所做的功较多
D.要由物块通过这段位移的时间决定
答案: A
2.如图所示,均匀长木板长l=40 cm,放在水平桌面上,它的右端与桌边相齐,木板质量为m=2 kg,与桌面间的动摩擦因数μ=0.2.今用水平推力F将其匀速推下桌子,则水平推力做功为(g取10 m/s2)( )
A.0.8 J B.1.6 J
C.8 J D.4 J
答案: A
3.质量为m的滑块,以一定初速度沿倾角为θ的斜面上滑L后,又沿原路返回,设滑块与斜面的动摩擦因数为μ,则滑块从开始上滑到滑回原点过程中,克服摩擦力所做的功为多少?重力做的功又为多少?
答案: 2μmgLcosθ 0
4.如图所示,水平传送带以2 m/s的速度匀速转动,将一质量为2 kg的工件轻放在传送带上,假设传送带的速度不变,且足够长.已知工件与传送带之间的动摩擦因数为0.2,则放手后工件在5 s内的位移是多少?摩擦力对工件做功是多少?(g取10 m/s2)
答案: 9 m 4 J
谢谢观看!
第1课时 功
问题导入
起重机竖直提升重物时,重物运动的方向与力的方向一致,则力对物体做的功为力的大小与重物移动距离的乘积。更普遍的情形是物体运动的方向与力的方向不一致,例如马拉雪橇时拉力方向和雪橇运动方向间有一个角度。这时应当怎样计算功呢?
知识梳理
一、功基本概念
1. 概念:一个物体受到力的作用,并在力的方向上发生了一段位移,这个力就对物体做了功。
?
?
?
?
2. 公式:W=Flcosα
(1)α是力与位移方向之间的夹角, l为物体在力作用下发生的位移;
(2)该公式一般用于求恒力做功。
3. 单位:焦(耳) 符号: J
(单位制换算: 1J=1N·m=1kg·m/s2·m=1kg·m2/s2)
?
二、正功和负功
二、正功和负功
1.矢标性:功是标量 ,正负号不表示大小,也不表示方向,表示对物体运动的促进或阻碍。
2.说明:某力做-5J功,可以说物体克服该力做了5J功
三、总功的计算
1.各个力分别对物体所做功的代数和。
公式:W合=WF1+WF2+…+WFn
2.几个力的合力对物体所做的功。
公式:W合=F合lcosα
(α为F合与位移l的夹角,F合为恒力)
二、行星运动的近似处理
行星的轨道与圆十分接近,在中学阶段的研究中我们按圆轨道处理,即:
1. 行星绕太阳运动的轨道十分接近圆,太阳处在圆心.
2.对某一行星来说,它绕太阳做圆周运动的角速度(或线速度大小)不变,即行星做匀速圆周运动.
3.所有行星轨道半径的三次方跟它的公转
周期的二次方的比值都相等,表达式为
判一判
(1)有力作用在物体上,并且物体也发生了位移时,力对物体一定做了功. (×)
(2)力对物体不做功,说明物体的位移一定为零. (×)
(3)力F1做功10 J,F2做功-15 J,力F1比F2做功少. (√)
重点突破
[例1](多选)一同学穿着旱冰鞋处于静止状态,推竖直墙壁后有了向后的速度,关于该同学推墙壁的过程,下列说法正确的是( )
A. 墙壁对该同学做正功
B. 墙壁对该同学没有做功
C. 该同学对墙壁做正功
D. 该同学对墙壁没有做功
任务一:对功的理解
答案:BD
答案: ABD
[变式训练1-1](多选)如图所示,物体静止在斜面上,现使物体随着斜面一起向右匀速运动,通过一段位移s,则( )
A. 静摩擦力对物体做了正功
B. 支持力对物体做了负功
C. 重力对物体做了正功
D. 合外力对物体做功为零
答案: D
[变式训练1-2]下列关于做功的说法正确的是 ( )
A. 凡是受力作用的物体,一定有力对物体做功
B. 凡是发生了位移的物体,一定有力对物体做功
C. 只要物体受力的同时又有位移发生,则一定有力对物体做功
D. 只要物体受力,又在力的方向上发生了位移,则一定有力对物体做功
[例2]如图所示,平行于斜面向上的拉力F使质量为m的物体匀速地沿着长为L,倾角为α的斜面的一端向上滑到另一端,物体与斜面间的动摩擦因数为μ,分别求作用在物体上各力对物体所做的功.
任务二:功的计算
[变式训练2-1] 一个质量m=2 kg的物体,受到与水平方向成37°角斜向上方的力F=10 N作用,在水平地面上移动的距离l=2 m,物体与地面间的滑动摩擦力Ff=4.2 N,求外力对物体所做的总功.(cos37°=0.8,sin37°=0.6)
解法一:
W1=Flcos37°=10×2×0.8 J=16 J
W2=Fflcos180°=-4.2×2 J=-8.4 J
W=W1+W2=7.6 J
解法二:
F合=Fcos37°-Ff=10×0.8 N-4.2 N=3.8 N
W=F合l=3.8×2 J=7.6 J.
[变式训练2-2]当上题中的拉力F= 100/3N时,物体刚好与地面接触且无压力,求物体在该力作用下从静止开始运动2 s过程中合力做的功.
1.功的计算
(1)计算功时首先应明确要求的是哪一个力的功,物体所受的各个力做功时互不影响。
(2)两种方法求总功:①W总=F合lcosα (几个力同时作用,均为恒力,一般做匀变速直线运动)
②W总=W1+W2+…+Wn (任何情况都可适用)
总结反思
巩固训练
1.在光滑水平面上推物块和在粗糙水平面上推物块相比较,如果所用的水平推力相同,物块在推力作用下通过的位移相同,则推力对物块所做的功( )
A.一样大
B.在光滑水平面上推力所做的功较多
C.在粗糙水平面上推力所做的功较多
D.要由物块通过这段位移的时间决定
答案: A
2.如图所示,均匀长木板长l=40 cm,放在水平桌面上,它的右端与桌边相齐,木板质量为m=2 kg,与桌面间的动摩擦因数μ=0.2.今用水平推力F将其匀速推下桌子,则水平推力做功为(g取10 m/s2)( )
A.0.8 J B.1.6 J
C.8 J D.4 J
答案: A
3.质量为m的滑块,以一定初速度沿倾角为θ的斜面上滑L后,又沿原路返回,设滑块与斜面的动摩擦因数为μ,则滑块从开始上滑到滑回原点过程中,克服摩擦力所做的功为多少?重力做的功又为多少?
答案: 2μmgLcosθ 0
4.如图所示,水平传送带以2 m/s的速度匀速转动,将一质量为2 kg的工件轻放在传送带上,假设传送带的速度不变,且足够长.已知工件与传送带之间的动摩擦因数为0.2,则放手后工件在5 s内的位移是多少?摩擦力对工件做功是多少?(g取10 m/s2)
答案: 9 m 4 J
谢谢观看!
