华东师大版 八年级上勾股定理(第一课时)课件
文档属性
| 名称 | 华东师大版 八年级上勾股定理(第一课时)课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 273.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-10 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
勾股定理
C
B
A
c
c
SC=S大正方形-4SRt△
SC=4SRt△
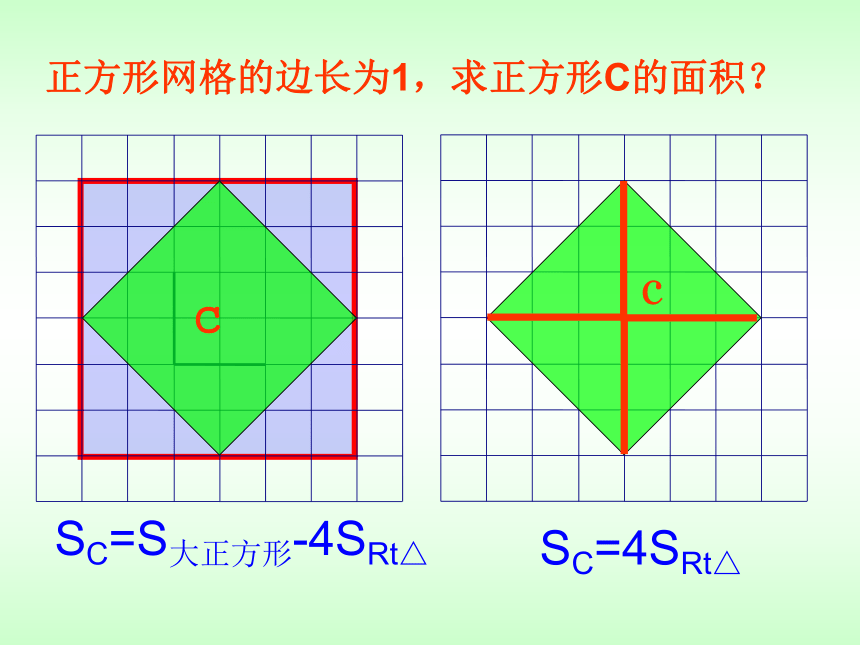
正方形网格的边长为1,求正方形C的面积?
B
A
C
图甲 图乙
A的面积
B的面积
C的面积
4
4
8
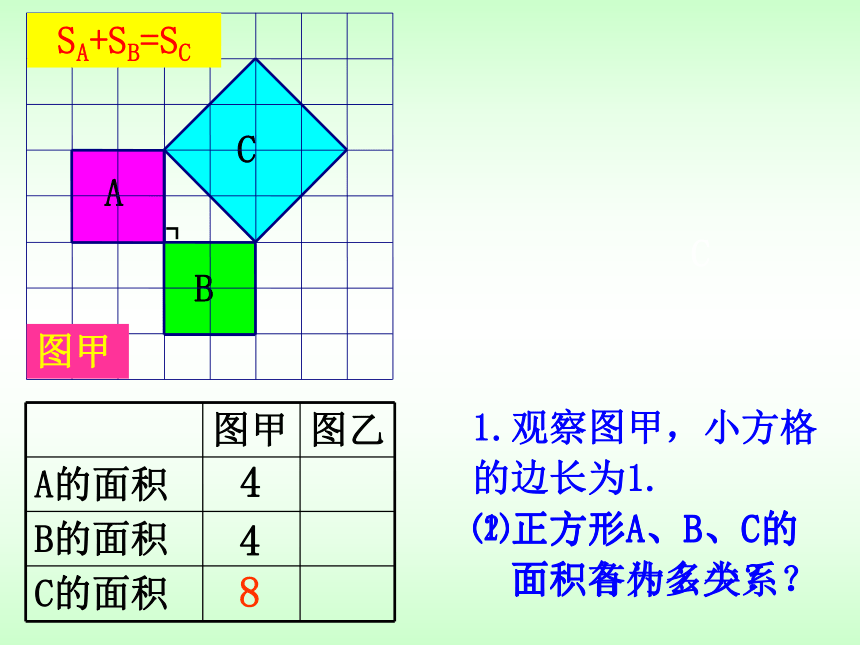
SA+SB=SC
C
图甲
1.观察图甲,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?
⑵正方形A、B、C的
面积有什么关系?
┓
A
B
C
图乙
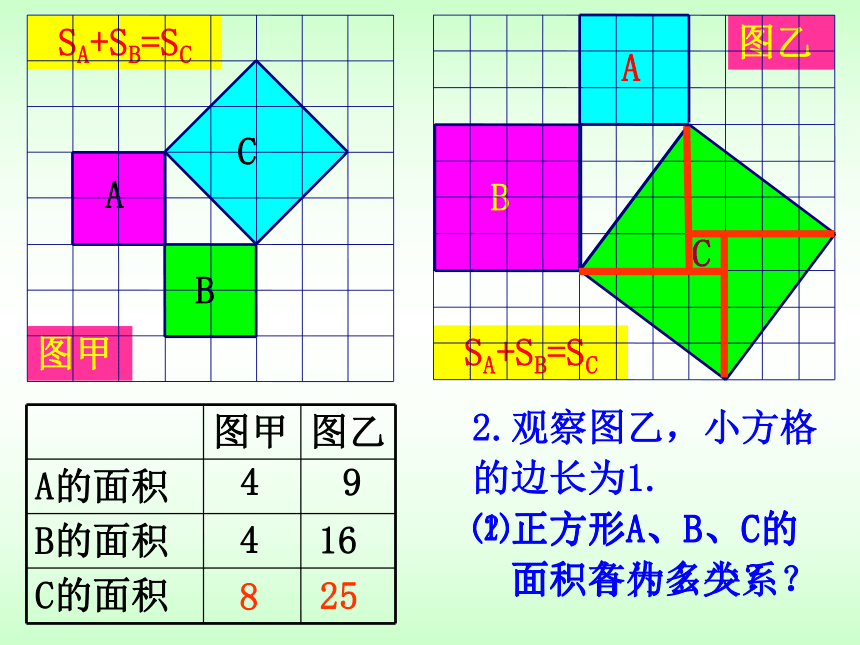
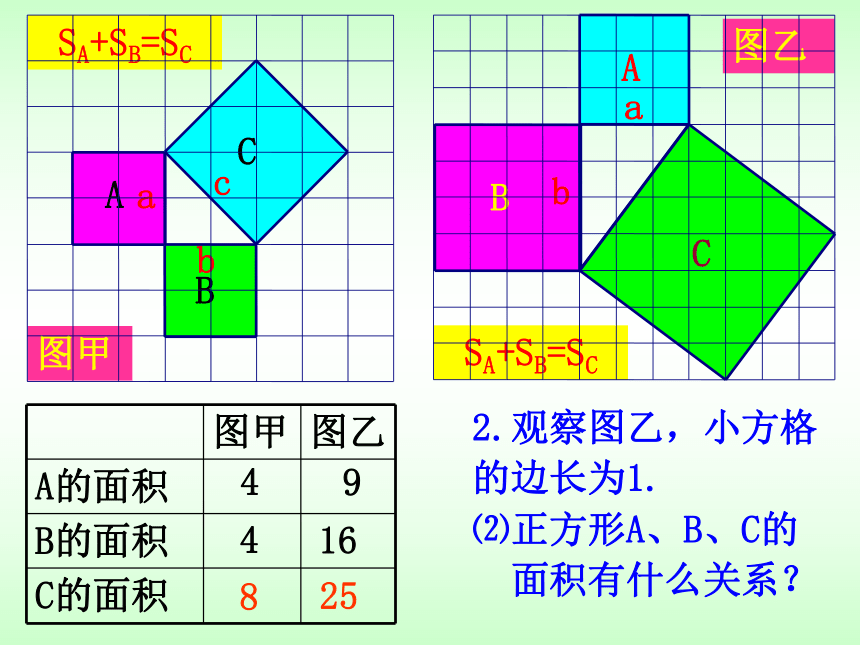
2.观察图乙,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?
9
16
25
SA+SB=SC
⑵正方形A、B、C的
面积有什么关系?
4
4
8
A
B
C
SA+SB=SC
图甲
图甲 图乙
A的面积
B的面积
C的面积
C
A
B
图乙
2.观察图乙,小方格
的边长为1.
9
16
25
SA+SB=SC
⑵正方形A、B、C的
面积有什么关系?
4
4
8
A
B
C
SA+SB=SC
图甲
图甲 图乙
A的面积
B的面积
C的面积
a
b
c
a
b
c
C
A
B
C
C
图乙
SA+SB=SC
SA+SB=SC
图甲
a
b
c
a
b
c
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
┓
┛
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
用拼图法证明
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
用拼图法证明
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
用拼图法证明
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
∵S大正方形=(a+b)2=a2+b2+2ab
S大正方形=4S直角三角形+ S小正方形
=4· ab + c2
=c2+2ab
∴a2+b2+2ab =c2+2ab
∴a2 +b2 =c2
a2+b2+2ab
c2+2ab
勾股定理
如果直角三角形两直角边分别为a, b,斜边为c,那么
即直角三角形两直角边的平方和等于
斜边的平方.
a
c
勾
弦
b
股
例1 .在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
例题分析
小结: 在直角三角形中,已知两边,可求第三边.
解:(1)∵∠C=90°,由勾股定理得:c2=a2+b2;
∴ c2= 62+82 =100
由c>0, 得 c=10
解:如图,在Rt△ABC中,BC=7米,AC=25米,由勾股定理得:
AB2+BC2=AC2
答:梯子上端A到墙的底边的垂直距离AB为24米。
∴AB2=AC2-BC2
例2、将长为25米的梯子斜靠在墙上, BC的长为7米,求梯子上端A到墙的底边的垂直距离AB。
2、查阅有关勾股定理的历史资料.
1、课堂作业:
教材习题,第1、2、3题;
3、思考题
勾股定理
C
B
A
c
c
SC=S大正方形-4SRt△
SC=4SRt△
正方形网格的边长为1,求正方形C的面积?
B
A
C
图甲 图乙
A的面积
B的面积
C的面积
4
4
8
SA+SB=SC
C
图甲
1.观察图甲,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?
⑵正方形A、B、C的
面积有什么关系?
┓
A
B
C
图乙
2.观察图乙,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?
9
16
25
SA+SB=SC
⑵正方形A、B、C的
面积有什么关系?
4
4
8
A
B
C
SA+SB=SC
图甲
图甲 图乙
A的面积
B的面积
C的面积
C
A
B
图乙
2.观察图乙,小方格
的边长为1.
9
16
25
SA+SB=SC
⑵正方形A、B、C的
面积有什么关系?
4
4
8
A
B
C
SA+SB=SC
图甲
图甲 图乙
A的面积
B的面积
C的面积
a
b
c
a
b
c
C
A
B
C
C
图乙
SA+SB=SC
SA+SB=SC
图甲
a
b
c
a
b
c
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
┓
┛
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
用拼图法证明
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
用拼图法证明
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
a
a
a
a
b
b
b
b
c
c
c
c
用拼图法证明
3.猜想a、b、c 之间的关系?
a2 +b2 =c2
∵S大正方形=(a+b)2=a2+b2+2ab
S大正方形=4S直角三角形+ S小正方形
=4· ab + c2
=c2+2ab
∴a2+b2+2ab =c2+2ab
∴a2 +b2 =c2
a2+b2+2ab
c2+2ab
勾股定理
如果直角三角形两直角边分别为a, b,斜边为c,那么
即直角三角形两直角边的平方和等于
斜边的平方.
a
c
勾
弦
b
股
例1 .在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
例题分析
小结: 在直角三角形中,已知两边,可求第三边.
解:(1)∵∠C=90°,由勾股定理得:c2=a2+b2;
∴ c2= 62+82 =100
由c>0, 得 c=10
解:如图,在Rt△ABC中,BC=7米,AC=25米,由勾股定理得:
AB2+BC2=AC2
答:梯子上端A到墙的底边的垂直距离AB为24米。
∴AB2=AC2-BC2
例2、将长为25米的梯子斜靠在墙上, BC的长为7米,求梯子上端A到墙的底边的垂直距离AB。
2、查阅有关勾股定理的历史资料.
1、课堂作业:
教材习题,第1、2、3题;
3、思考题
