7.2 二元一次方程组的解法(1)代入法课件
文档属性
| 名称 | 7.2 二元一次方程组的解法(1)代入法课件 |  | |
| 格式 | zip | ||
| 文件大小 | 172.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-10 20:41:07 | ||
图片预览






文档简介
(共16张PPT)
7.2 二元一次方程组的解法 (第1课时)
华东师大版七年级(下册)
1、指出 三对数值分别是下面哪一
个方程组的解.
x =1,
y = 2,
x = 2,
y = -2,
x = -1,
y = 2,
① ② ③
y + 2x = 0
x + 2y = 3
x – y = 4
x + y = 0
y = 2x
x + y = 3
解:
①( )是方程组( )的解;
②( )是方程组( )的解;
③( )是方程组( )的解;
x =1,
y = 2,
y = 2x
x + y = 3
x = 2,
y = -2,
x – y = 4
x + y = 0
x = -1,
y = 2,
y + 2x = 0
x + 2y = 3
口 答 题
2、若 是关于 x、y 的方程 5x +ay = 1 的解,则a=( )
x = -1,
y = 2,
3、方程组 的解是
y + z = 180
y - z = ( )
y = 100
z =( ),
4、若关于x、y 的二元一次方程组 的
解x 与 y 的值相等,则k =( )
4x – 3y = 1
kx +(k – 1)y = 3
口 答 题
3
80
20
2
二元一次方程组中各个方程的解一定是方程组的解 ( )
方程组的解一定是组成这个方程组的每一个方程的解 ( )
判 断
错
对
已知方程
先用含x的代数式表示y,再用含y 的代数式表示x.并比较哪一种形式比较简单.
选择题:二元一次方程组
的解是( )
B.
C.
D.
A.
某校现有校舍20000m2,计划拆除部分旧校舍,改建新校舍,使校舍总面积增加30%.若建造新校舍的面积为被拆除的旧校舍面积的4倍,那么应该拆除多少旧校舍,建造多少新校舍?(单位为m2)
①
②
如果设应拆除上校舍xm2,建造新校舍ym2,那么根据题意可列出方程组
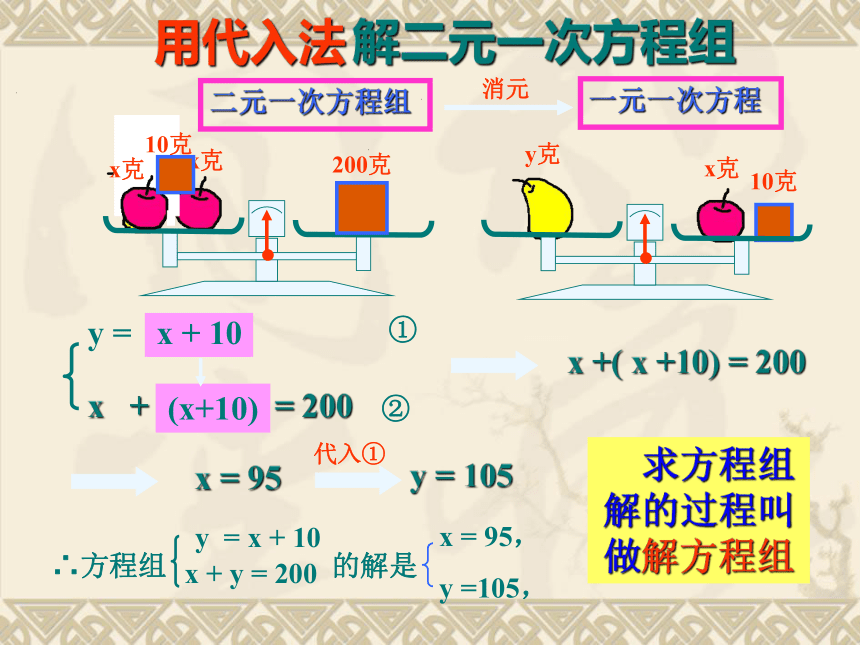
y克
.
.
x克
200克
y克
x克
10克
x + y = 200
y = x + 10
解二元一次方程组
一元一次方程
二元一次方程组
消元
用代入法
x克
10克
(x+10)
x +( x +10) = 200
①
②
x = 95
代入①
y = 105
∴方程组 的解是
y = x + 10
x + y = 200
x = 95,
y =105,
求方程组解的过程叫做解方程组
分析
解方程组
y –x = 20000×30%
y = 4x
解:
①
②
把②代入①得:
4x–x = 20000×30%
3x = 6000
x = 2000
把x=2000代入②,得:
y= 4x
= 4×2000
= 8000
∴
x = 2000
y = 8000
y –x= 20000×30%
y = 4x
4x
y –x = 20000×30%
y = 4x
解方程组
y –x = 20000×30%
y = 4x
解:
①
②
把②代入①得:
4x–x = 20000×30%
3x = 6000
x = 2000
把x=2000代入②,得:
y= 4x
= 4×2000
= 8000
∴
x = 2000
y = 8000
y –x = 20000×30%
y = 4x
练 习 题
解方程组
例1 解方程组
x+y = 7
3x + y = 17
解:
①
②
x +y = 7
3x + y = 17
由 ①得:
y = 7 -x
③
把③代入②得:
3x +(7-x)= 17
即 x = 5
把x = 5代入③,得
y =7-x
=7-5
= 2
∴
x = 5
y = 2
例1 解方程组
x+y = 7
3x + y = 17
解:
①
②
x +y = 7
3x + y = 17
由 ①得:
y = 7 -x
③
把③代入②得:
3x +(7-x)= 17
即 x = 5
把x = 5代入③,得
y =7-x
=7-5
= 2
∴
x = 5
y = 2
练 习 题
解方程组
思 考
请你概括一下上面解法的思路,并想想,怎样解方程组:
上面的解法,是由二元一次方程组中一个方程,将一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解,这种方法叫代入消元法,简称代入法。
归 纳
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数(变)
2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值(代)
3、把这个未知数的值代入一次式,求得另一个未知数的值(求)
4、写出方程组的解(写)
用代入法解二元一次方程组的一般步骤
解二元一次方程组
用代入法
爱学数学
爱数学周报
再见
7.2 二元一次方程组的解法 (第1课时)
华东师大版七年级(下册)
1、指出 三对数值分别是下面哪一
个方程组的解.
x =1,
y = 2,
x = 2,
y = -2,
x = -1,
y = 2,
① ② ③
y + 2x = 0
x + 2y = 3
x – y = 4
x + y = 0
y = 2x
x + y = 3
解:
①( )是方程组( )的解;
②( )是方程组( )的解;
③( )是方程组( )的解;
x =1,
y = 2,
y = 2x
x + y = 3
x = 2,
y = -2,
x – y = 4
x + y = 0
x = -1,
y = 2,
y + 2x = 0
x + 2y = 3
口 答 题
2、若 是关于 x、y 的方程 5x +ay = 1 的解,则a=( )
x = -1,
y = 2,
3、方程组 的解是
y + z = 180
y - z = ( )
y = 100
z =( ),
4、若关于x、y 的二元一次方程组 的
解x 与 y 的值相等,则k =( )
4x – 3y = 1
kx +(k – 1)y = 3
口 答 题
3
80
20
2
二元一次方程组中各个方程的解一定是方程组的解 ( )
方程组的解一定是组成这个方程组的每一个方程的解 ( )
判 断
错
对
已知方程
先用含x的代数式表示y,再用含y 的代数式表示x.并比较哪一种形式比较简单.
选择题:二元一次方程组
的解是( )
B.
C.
D.
A.
某校现有校舍20000m2,计划拆除部分旧校舍,改建新校舍,使校舍总面积增加30%.若建造新校舍的面积为被拆除的旧校舍面积的4倍,那么应该拆除多少旧校舍,建造多少新校舍?(单位为m2)
①
②
如果设应拆除上校舍xm2,建造新校舍ym2,那么根据题意可列出方程组
y克
.
.
x克
200克
y克
x克
10克
x + y = 200
y = x + 10
解二元一次方程组
一元一次方程
二元一次方程组
消元
用代入法
x克
10克
(x+10)
x +( x +10) = 200
①
②
x = 95
代入①
y = 105
∴方程组 的解是
y = x + 10
x + y = 200
x = 95,
y =105,
求方程组解的过程叫做解方程组
分析
解方程组
y –x = 20000×30%
y = 4x
解:
①
②
把②代入①得:
4x–x = 20000×30%
3x = 6000
x = 2000
把x=2000代入②,得:
y= 4x
= 4×2000
= 8000
∴
x = 2000
y = 8000
y –x= 20000×30%
y = 4x
4x
y –x = 20000×30%
y = 4x
解方程组
y –x = 20000×30%
y = 4x
解:
①
②
把②代入①得:
4x–x = 20000×30%
3x = 6000
x = 2000
把x=2000代入②,得:
y= 4x
= 4×2000
= 8000
∴
x = 2000
y = 8000
y –x = 20000×30%
y = 4x
练 习 题
解方程组
例1 解方程组
x+y = 7
3x + y = 17
解:
①
②
x +y = 7
3x + y = 17
由 ①得:
y = 7 -x
③
把③代入②得:
3x +(7-x)= 17
即 x = 5
把x = 5代入③,得
y =7-x
=7-5
= 2
∴
x = 5
y = 2
例1 解方程组
x+y = 7
3x + y = 17
解:
①
②
x +y = 7
3x + y = 17
由 ①得:
y = 7 -x
③
把③代入②得:
3x +(7-x)= 17
即 x = 5
把x = 5代入③,得
y =7-x
=7-5
= 2
∴
x = 5
y = 2
练 习 题
解方程组
思 考
请你概括一下上面解法的思路,并想想,怎样解方程组:
上面的解法,是由二元一次方程组中一个方程,将一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解,这种方法叫代入消元法,简称代入法。
归 纳
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数(变)
2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值(代)
3、把这个未知数的值代入一次式,求得另一个未知数的值(求)
4、写出方程组的解(写)
用代入法解二元一次方程组的一般步骤
解二元一次方程组
用代入法
爱学数学
爱数学周报
再见
