8.6.3 平面与平面垂直(2)课件(共16张PPT)
文档属性
| 名称 | 8.6.3 平面与平面垂直(2)课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-05 19:10:17 | ||
图片预览






文档简介
第8章 立体几何初步
8.6.3 平面与平面垂直(2)
高中数学人教A版(2019)必修第二册
知识点一 面面垂直的条件缺漏,混淆致错
1,如图,在梯形????????????????中,????????//????????,????,????是线段????????上的点,且?????????⊥ ?????????,????????⊥????????,????????=????????,????????=????,????????=????????,????????=????,现将Δ????????????,Δ????????????分别沿????????,????????折起,使????,????两点重合于点????,得到多面体????????????????????,求证:平面????????????⊥平面????????????.
?
由已知可得????????=????,????????=????,????????=5,则折叠后????????=????,????????=????,????????=5,所以????????⊥????????.
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
在梯形ABCD中,CF⊥AB,则折叠后CF⊥EF,CF⊥FG.又EF∩FG=F,EF,FG?平面EFG,所以CF⊥平面EFG,所以CF⊥EG.
?
又GF∩CG=F,GF,CG?平面CFG,所以EG⊥平面CFG
?
又EG?平面DEG,所以平面DEG⊥平面CFG
?
探究新知
面面垂直的条件缺漏,混淆致错
证明时要充分利用面面垂直、线面垂直、线线垂直相互转化,如果有面面垂直、先在其中一个面内作交线的垂线,有时题中就有这样的垂线,如果没有就要做辅助垂线.推出线面垂直、再和线线垂直进行循环证明.谨防把线面垂直的判定误认为垂直于两条线,就会得到线面垂直(必须是垂直于两条相交线),把面面垂直的性质定理误认为两平面内的任意两条直线都垂直;把面面垂直的判定误认为两平面内的两条直线垂直,则两平面垂直.
知识点2 线面、面面垂直的性质定理条件缺漏,混淆致错
2,设????,????是两条不同的直线,????,????是两个不同的平面,下列正确的是( )
若????⊥????,?????????, ?????????,则 ????⊥????
若????//????, ?????????, ?????????,则 ????//????
若????⊥????,?????????, ?????????,则 ????⊥????
若????⊥????, ????//???? , ????//????,则 ????⊥????
?
对于????, ????,????可能为平行,垂直,异面直线,故????错误;
?
对于????, ????,????可能为平行,垂直,异面直线,故????错误;
?
对于????, ????应与????中两条相交直线垂直时结论才成立,故????错误;
?
故选????
?
????
?
探究新知
1,如图,在三棱锥?????????????????中,若????????=????????, ????????=????????,????是的????????中点,则下列说法正确的是__________
?
题①
——平面与平面垂直的判定与证明
因为AB=CB,且E是AC的中点,所以BE⊥AC,同理有DE⊥AC.又DE∩BE=E,DE,BE?平面BDE,所以AC⊥平面BDE.因为AC?平面ABC,所以平面ABC⊥平面BDE.又由于AC ?平面ACD,所以平面ACD⊥平面BDE,只有③正确
?
????
?
????
?
????
?
????
?
????
?
①平面ABC⊥平面ABD
②平面ABD⊥平面BCD
③平面ABC⊥平面BDE,且平面ACD⊥平面BDE
④平面ABC⊥平面ACD,且平面ACD⊥平面BDE
③
例题讲解
2, 如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把ΔABD和ΔACD折成互相垂直的两个平面后,卢老师的学生得出如下四个结论:①BD⊥AC;②ΔABC是等边三角形; ③三棱锥D-ABC是正三棱锥; ④平面ADC⊥平面ABC. 其中正确的有__________.
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
由题意知,BD⊥平面ADC,故BD⊥AC,①正确;
AD为等腰直角三角形ABC斜边上的高,平面ABD⊥平面ACD,所以AB=BC=AC,所以ΔABC为等边三角形,②正确;
易知DA=DB=DC,由②知,③正确;
由①知④错误,所以正确的有①②③
① ② ③
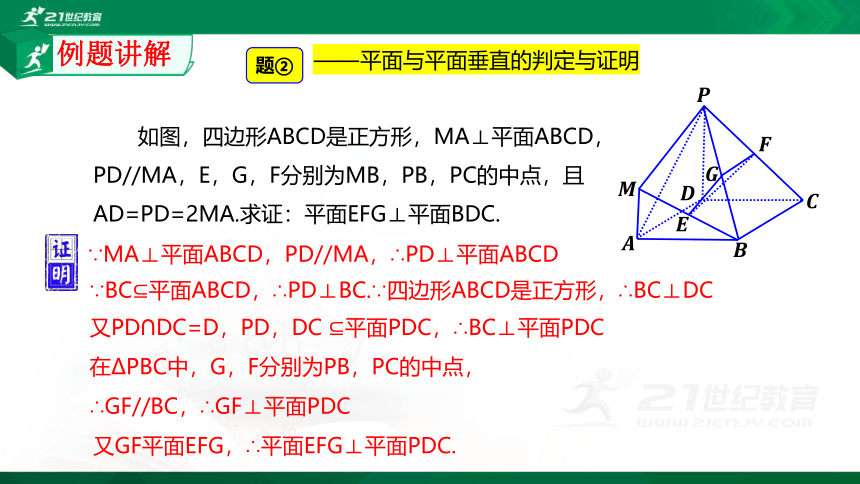
如图,四边形ABCD是正方形,MA⊥平面ABCD,PD//MA,E,G,F分别为MB,PB,PC的中点,且AD=PD=2MA.求证:平面EFG⊥平面BDC.
题②
——平面与平面垂直的判定与证明
∵MA⊥平面ABCD,PD//MA,∴PD⊥平面ABCD
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
∵BC?平面ABCD,∴PD⊥BC.∵四边形ABCD是正方形,∴BC⊥DC
?
又PD∩DC=D,PD,DC ?平面PDC,∴BC⊥平面PDC
?
在ΔPBC中,G,F分别为PB,PC的中点,
∴GF//BC,∴GF⊥平面PDC
又GF平面EFG,∴平面EFG⊥平面PDC.
例题讲解
1, 如图,四边形ABCD是矩形,BC⊥平面ABE,且AE=2,EB=BC=23.点F为CE上一点, 且BF⊥平面BCE,求三棱锥A-DBE的体积.
?
题③
——二面角
∵BF⊥平面ACE,AE?平面ACE,∴BF⊥AE
?
????
?
????
?
????
?
????
?
????
?
????
?
∵BC⊥平面ABE,AE?平面ABE,∴BC⊥AE
?
∵BC∩BF=B,BC,BF?平面BCE,∴AE⊥平面BCE,∴AE⊥BE
?
又∵BC//AD,∴AD⊥平面ABE
∴VA-DBE=VD-ABE=13SΔABE= 13×12×2×23×2= 433
?
即三棱锥A-DBE的体积为433
?
例题讲解
2,如图所示,将等腰直角三角形ABC沿着斜边BC上的高AD折成一个二面角,使得∠B′AC=60°,则二面角B′-AD-C的大小是多少度?
????
?
????′
?
????
?
????
?
连接B′C,∵ AD是等腰直角三角形ABC斜边上的高,
∴ BD=DC=22AC,∠ADC=∠ADB=90°
?
∴ ∠B′DC是二面角B′-AD-C的平面角.
∵ ∠B′AC=60°,∴ ΔB′AC是等边三角形
∴ B′C=AB′=AC,在ΔB′DC中,∠B′DC=90°.
1, 如图,在三棱锥P-ABC中,平面PAB⊥平面PAC,AB⊥BP,M,N分别为PA,AB的中点.AC=PC.求证:AB⊥平面CMN.
题③
——平面与平面垂直的性质定理的应用
在平面PAB中,AB⊥BP,MN//PB,∴AB⊥MN
????
?
????
?
????
?
????
?
????
?
????
?
∵AC=PC,M为PA的中点,所以CM⊥PA
又平面PAC⊥平面PAC,平面PAB∩平面PAC=PA,CM?平面PAC
?
∴ CM⊥平面PAB
∵ AB ?平面PAB,∴CM⊥AB.又 ∵CM∩MN=M,MN平面CMN,
?
∴ AB⊥平面CMN
例题讲解
2, 如图,在四棱锥P-ABCD中,底面ABCD是边长为 ???? 的正方形,侧面PAD⊥底面ABCD,且PA=PD= 22?AD.求证:平面PAB⊥平面PBD.
?
????
?
????
?
????
?
????
?
∵ 平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,AB⊥AD,
AB?平面ABCD,∴ AB⊥平面PAD
?
又PD?平面PAD,∴ PD⊥AB. ∵ PA=PD=22?AD,∴PA2+PD2=AD2.
?
????
?
∴ PA⊥PD. 又PA∩AB=A,∴ PD⊥平面PAB
∵ PD?平面PBD,∴ 平面PAB⊥平面PBD
?
如图,在直角梯形ABCD中,AB//CD,AB⊥BE,E为AB上的点, 且AD=AE=DC=2,BE=1,将ΔADE沿DE折叠到点P ,使PC=PB,求证:平面PDE⊥平面ABCD.
题④
——平面图形折叠后的垂直问题
如图,取BC的中点G,DE的中点H,连接PG,GH,HP.
????
?
????
?
????
?
????
?
????
?
????
?
∴ HG//AB,∵AB⊥BC,∴HG⊥BC.∵PB=PC,∴PG⊥BC.
又HG∩PG=G,HG,PG ?平面PGH,∴BC⊥平面PGH
?
又PH?平面PGH,∴PH⊥BC,∵PD=AD=AE=PE,H是DE的中点, ∴ PH⊥DE.
?
∵BE//DC,且DC=2BE,所以DE与BC必相交,且DE,BC?平面BCDE,∴PH⊥平面BCDE
?
又PH?平面PDE,∴平面PDE⊥平面BCDE,即平面PDE⊥平面ABCD
?
????
?
????
?
例题讲解
如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为的菱形,ΔPAD为等边三角形,且其所在平面⊥平面ABCD,求证:AD⊥PB
题⑤
——线面,面面垂直的综合应用
取AD的中点G,连接PG,BG,如图
∵ ΔPAD为等边三角形,∴ PG⊥AD
在菱形ABCD中,∠DAB=60°,G为AD中点,
∴BG⊥AD
又BG∩PG=G,BG,PG?平面PGB
?
∴ AD⊥平面PGB,∵ PB?平面PGB,∴ AD⊥PB
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
例题讲解
∵ ΔPAB是等边三角形,∴ PB=PA
又∵ ∠PAC=∠PBC=90°,PC=PC
∴ RtΔPBC≌RtΔPAC. ∴ AC=BC
????
?
????
?
????
?
????
?
如图,取AB中点D,连接PD,CD,
则PD⊥AB,CD⊥AB,又PD∩CD=D
如图,在三棱锥P-ABC中,ΔPAB是等边三角形∠PAC=∠PBC=90°,求证:AB⊥PC.
∴ AB⊥平面PDC,∴ AB⊥PC
????
?
谢谢聆听
8.6.3 平面与平面垂直(2)
高中数学人教A版(2019)必修第二册
知识点一 面面垂直的条件缺漏,混淆致错
1,如图,在梯形????????????????中,????????//????????,????,????是线段????????上的点,且?????????⊥ ?????????,????????⊥????????,????????=????????,????????=????,????????=????????,????????=????,现将Δ????????????,Δ????????????分别沿????????,????????折起,使????,????两点重合于点????,得到多面体????????????????????,求证:平面????????????⊥平面????????????.
?
由已知可得????????=????,????????=????,????????=5,则折叠后????????=????,????????=????,????????=5,所以????????⊥????????.
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
在梯形ABCD中,CF⊥AB,则折叠后CF⊥EF,CF⊥FG.又EF∩FG=F,EF,FG?平面EFG,所以CF⊥平面EFG,所以CF⊥EG.
?
又GF∩CG=F,GF,CG?平面CFG,所以EG⊥平面CFG
?
又EG?平面DEG,所以平面DEG⊥平面CFG
?
探究新知
面面垂直的条件缺漏,混淆致错
证明时要充分利用面面垂直、线面垂直、线线垂直相互转化,如果有面面垂直、先在其中一个面内作交线的垂线,有时题中就有这样的垂线,如果没有就要做辅助垂线.推出线面垂直、再和线线垂直进行循环证明.谨防把线面垂直的判定误认为垂直于两条线,就会得到线面垂直(必须是垂直于两条相交线),把面面垂直的性质定理误认为两平面内的任意两条直线都垂直;把面面垂直的判定误认为两平面内的两条直线垂直,则两平面垂直.
知识点2 线面、面面垂直的性质定理条件缺漏,混淆致错
2,设????,????是两条不同的直线,????,????是两个不同的平面,下列正确的是( )
若????⊥????,?????????, ?????????,则 ????⊥????
若????//????, ?????????, ?????????,则 ????//????
若????⊥????,?????????, ?????????,则 ????⊥????
若????⊥????, ????//???? , ????//????,则 ????⊥????
?
对于????, ????,????可能为平行,垂直,异面直线,故????错误;
?
对于????, ????,????可能为平行,垂直,异面直线,故????错误;
?
对于????, ????应与????中两条相交直线垂直时结论才成立,故????错误;
?
故选????
?
????
?
探究新知
1,如图,在三棱锥?????????????????中,若????????=????????, ????????=????????,????是的????????中点,则下列说法正确的是__________
?
题①
——平面与平面垂直的判定与证明
因为AB=CB,且E是AC的中点,所以BE⊥AC,同理有DE⊥AC.又DE∩BE=E,DE,BE?平面BDE,所以AC⊥平面BDE.因为AC?平面ABC,所以平面ABC⊥平面BDE.又由于AC ?平面ACD,所以平面ACD⊥平面BDE,只有③正确
?
????
?
????
?
????
?
????
?
????
?
①平面ABC⊥平面ABD
②平面ABD⊥平面BCD
③平面ABC⊥平面BDE,且平面ACD⊥平面BDE
④平面ABC⊥平面ACD,且平面ACD⊥平面BDE
③
例题讲解
2, 如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把ΔABD和ΔACD折成互相垂直的两个平面后,卢老师的学生得出如下四个结论:①BD⊥AC;②ΔABC是等边三角形; ③三棱锥D-ABC是正三棱锥; ④平面ADC⊥平面ABC. 其中正确的有__________.
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
由题意知,BD⊥平面ADC,故BD⊥AC,①正确;
AD为等腰直角三角形ABC斜边上的高,平面ABD⊥平面ACD,所以AB=BC=AC,所以ΔABC为等边三角形,②正确;
易知DA=DB=DC,由②知,③正确;
由①知④错误,所以正确的有①②③
① ② ③
如图,四边形ABCD是正方形,MA⊥平面ABCD,PD//MA,E,G,F分别为MB,PB,PC的中点,且AD=PD=2MA.求证:平面EFG⊥平面BDC.
题②
——平面与平面垂直的判定与证明
∵MA⊥平面ABCD,PD//MA,∴PD⊥平面ABCD
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
∵BC?平面ABCD,∴PD⊥BC.∵四边形ABCD是正方形,∴BC⊥DC
?
又PD∩DC=D,PD,DC ?平面PDC,∴BC⊥平面PDC
?
在ΔPBC中,G,F分别为PB,PC的中点,
∴GF//BC,∴GF⊥平面PDC
又GF平面EFG,∴平面EFG⊥平面PDC.
例题讲解
1, 如图,四边形ABCD是矩形,BC⊥平面ABE,且AE=2,EB=BC=23.点F为CE上一点, 且BF⊥平面BCE,求三棱锥A-DBE的体积.
?
题③
——二面角
∵BF⊥平面ACE,AE?平面ACE,∴BF⊥AE
?
????
?
????
?
????
?
????
?
????
?
????
?
∵BC⊥平面ABE,AE?平面ABE,∴BC⊥AE
?
∵BC∩BF=B,BC,BF?平面BCE,∴AE⊥平面BCE,∴AE⊥BE
?
又∵BC//AD,∴AD⊥平面ABE
∴VA-DBE=VD-ABE=13SΔABE= 13×12×2×23×2= 433
?
即三棱锥A-DBE的体积为433
?
例题讲解
2,如图所示,将等腰直角三角形ABC沿着斜边BC上的高AD折成一个二面角,使得∠B′AC=60°,则二面角B′-AD-C的大小是多少度?
????
?
????′
?
????
?
????
?
连接B′C,∵ AD是等腰直角三角形ABC斜边上的高,
∴ BD=DC=22AC,∠ADC=∠ADB=90°
?
∴ ∠B′DC是二面角B′-AD-C的平面角.
∵ ∠B′AC=60°,∴ ΔB′AC是等边三角形
∴ B′C=AB′=AC,在ΔB′DC中,∠B′DC=90°.
1, 如图,在三棱锥P-ABC中,平面PAB⊥平面PAC,AB⊥BP,M,N分别为PA,AB的中点.AC=PC.求证:AB⊥平面CMN.
题③
——平面与平面垂直的性质定理的应用
在平面PAB中,AB⊥BP,MN//PB,∴AB⊥MN
????
?
????
?
????
?
????
?
????
?
????
?
∵AC=PC,M为PA的中点,所以CM⊥PA
又平面PAC⊥平面PAC,平面PAB∩平面PAC=PA,CM?平面PAC
?
∴ CM⊥平面PAB
∵ AB ?平面PAB,∴CM⊥AB.又 ∵CM∩MN=M,MN平面CMN,
?
∴ AB⊥平面CMN
例题讲解
2, 如图,在四棱锥P-ABCD中,底面ABCD是边长为 ???? 的正方形,侧面PAD⊥底面ABCD,且PA=PD= 22?AD.求证:平面PAB⊥平面PBD.
?
????
?
????
?
????
?
????
?
∵ 平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,AB⊥AD,
AB?平面ABCD,∴ AB⊥平面PAD
?
又PD?平面PAD,∴ PD⊥AB. ∵ PA=PD=22?AD,∴PA2+PD2=AD2.
?
????
?
∴ PA⊥PD. 又PA∩AB=A,∴ PD⊥平面PAB
∵ PD?平面PBD,∴ 平面PAB⊥平面PBD
?
如图,在直角梯形ABCD中,AB//CD,AB⊥BE,E为AB上的点, 且AD=AE=DC=2,BE=1,将ΔADE沿DE折叠到点P ,使PC=PB,求证:平面PDE⊥平面ABCD.
题④
——平面图形折叠后的垂直问题
如图,取BC的中点G,DE的中点H,连接PG,GH,HP.
????
?
????
?
????
?
????
?
????
?
????
?
∴ HG//AB,∵AB⊥BC,∴HG⊥BC.∵PB=PC,∴PG⊥BC.
又HG∩PG=G,HG,PG ?平面PGH,∴BC⊥平面PGH
?
又PH?平面PGH,∴PH⊥BC,∵PD=AD=AE=PE,H是DE的中点, ∴ PH⊥DE.
?
∵BE//DC,且DC=2BE,所以DE与BC必相交,且DE,BC?平面BCDE,∴PH⊥平面BCDE
?
又PH?平面PDE,∴平面PDE⊥平面BCDE,即平面PDE⊥平面ABCD
?
????
?
????
?
例题讲解
如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为的菱形,ΔPAD为等边三角形,且其所在平面⊥平面ABCD,求证:AD⊥PB
题⑤
——线面,面面垂直的综合应用
取AD的中点G,连接PG,BG,如图
∵ ΔPAD为等边三角形,∴ PG⊥AD
在菱形ABCD中,∠DAB=60°,G为AD中点,
∴BG⊥AD
又BG∩PG=G,BG,PG?平面PGB
?
∴ AD⊥平面PGB,∵ PB?平面PGB,∴ AD⊥PB
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
例题讲解
∵ ΔPAB是等边三角形,∴ PB=PA
又∵ ∠PAC=∠PBC=90°,PC=PC
∴ RtΔPBC≌RtΔPAC. ∴ AC=BC
????
?
????
?
????
?
????
?
如图,取AB中点D,连接PD,CD,
则PD⊥AB,CD⊥AB,又PD∩CD=D
如图,在三棱锥P-ABC中,ΔPAB是等边三角形∠PAC=∠PBC=90°,求证:AB⊥PC.
∴ AB⊥平面PDC,∴ AB⊥PC
????
?
谢谢聆听
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
