8.6.1-8.6.2 直线与直线垂直、直线与平面垂直-课件(共22张PPT)
文档属性
| 名称 | 8.6.1-8.6.2 直线与直线垂直、直线与平面垂直-课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-05 19:13:50 | ||
图片预览






文档简介
第8章 立体几何初步
8.6.1-8.6.2 直线与直线
垂直、直线与平面垂直
????
?
????
?
????
?
????′
?
????
?
????
?
????
?
????
?
????
?
????????
?
????????
?
????????
?
????????
?
????
?
????
?
????
?
????
?
高中数学人教A版(2019)必修第二册
异面直线所成的角
已知两条异面直线a,b,经过空间任意一点O分别作直线a′//a, b′// b?,我们把直线a′与b′所成的角叫做异面直线a与b所成的角(或夹角).
?
异面直线所成角的概念
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????′
?
????
?
探究新知
异面直线所成的角
异面直线所成角的概念
异面直线所成的角的范围:由异面直线所成角的定义得,异面直线所成的角θ是锐角或者直角,即0°<θ ≤90°
研究异面直线所成的角,就是通过平移把异面直线转化为相交直线,把空间角问题转化为平面角问题,这是研究立体几何问题的一种基本思想,即空间问题平面化.
异面直线所成的角的大小不能是0°,当两条直线所成的角是0°时,这两条直线共面.
异面直线所成的角
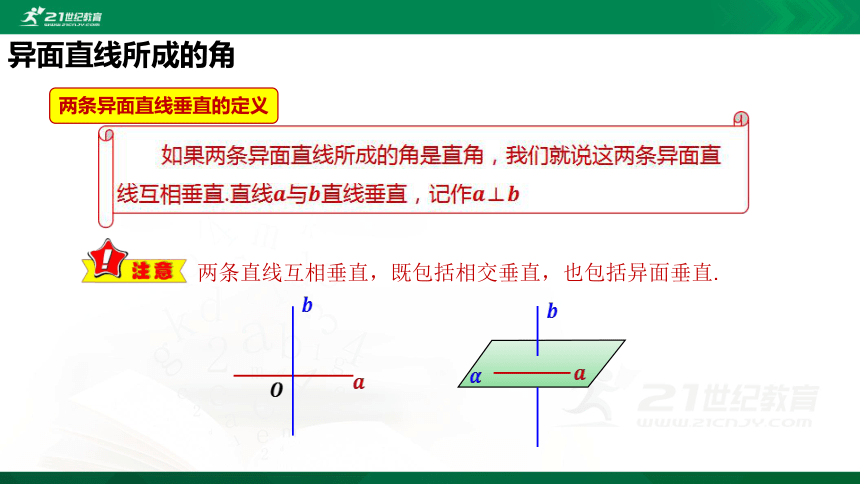
如果两条异面直线所成的角是直角,我们就说这两条异面直线互相垂直.直线????与????直线垂直,记作????⊥????
?
两条异面直线垂直的定义
????
?
????
?
????
?
????
?
????
?
????
?
两条直线互相垂直,既包括相交垂直,也包括异面垂直.
异面直线所成的角
异面直线所成角的求解步骤
证明:证明作出的角就是要求解的角
构造:根据异面直线的定义,用平移法(常利用三角形中位线、平行四边形的性质)作出异面直线所成的角.
计算:求角度(常利用三角形的有关知识)
结论:若求出的角是锐角或者直角,则它就是所求异面直线所成的角;若求出的角是钝角,则它的补角就是所求异面直线所成的角.
异面直线所成的角
异面直线所成角的求解步骤
如图所示,已知正方体?????????????????????????????????????????????????,则异面直线????????????????与????????????所成的角的大小是多少?
?
????
?
????
?
????
?
????
?
????????
?
????????
?
????????
?
????????
?
连接????1????和????1????,∵ ????1????// ????1?????,
?
∴ ∠????1????1????为异面直线????1????1与????1????所成的角.
?
∵ ????1????,????1????1,????1????为正方体各面的对角线,
?
∴ ????1????=????1????1=????1????,∴ Δ????1????1????为正三角形,∴∠????1????1????=????????°
?
∴ 异面直线????1????1与????1????所成的角为60°.
?
直线与平面垂直
一般地,如果直线和平面内的任意一条直线都垂直,我们就说直线与平面互相垂直,记作⊥.直线叫做平面的垂线,平面叫做直线的垂面.直线与平面垂直时,它们唯一的公共点叫做垂足.
可以发现,过一点垂直于已知平面的直线有且只有一条.
直线与平面垂直是直线与平面相交的一种特殊情况.
定义中的“任意一条直线”与“所有直线”是同义词,但与“无数条直线”不同.定义的实质就是直线与平面内的所有直线都垂直.
运用直线与平面垂直的定义来判定直线与平面垂直时,要紧扣“一条直线与一个平面内的任意一条直线都垂直”这个条件.
探究新知
直线与平面垂直
图形语言:
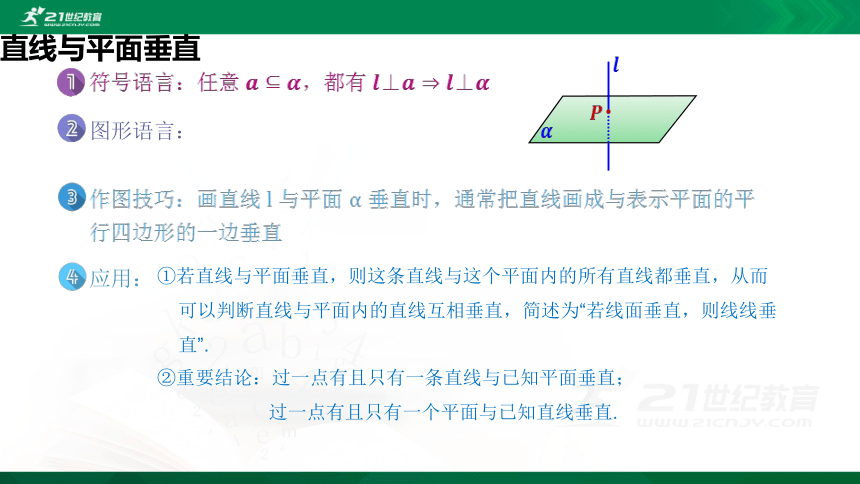
符号语言:任意 ?????????,都有 ????⊥?????????⊥????
?
作图技巧:画直线 l 与平面 α 垂直时,通常把直线画成与表示平面的平行四边形的一边垂直
?
????
?
????
?
????
?
应用:
①若直线与平面垂直,则这条直线与这个平面内的所有直线都垂直,从而
可以判断直线与平面内的直线互相垂直,简述为“若线面垂直,则线线垂
直”.
②重要结论:过一点有且只有一条直线与已知平面垂直;
过一点有且只有一个平面与已知直线垂直.
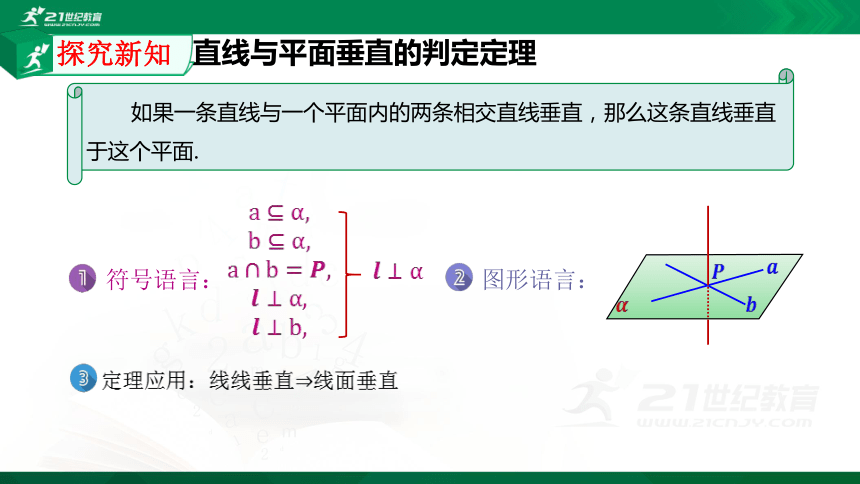
直线与平面垂直的判定定理
如果一条直线与一个平面内的两条相交直线垂直,那么这条直线垂直于这个平面.
图形语言:
符号语言:
a?α,
b?α,
a∩b=????,
????⊥α,
????⊥b,
?
????⊥α?
?
????
?
????
?
????
?
????
?
定理应用:线线垂直?线面垂直
?
探究新知
直线与平面垂直的判定定理
判定定理的条件中“平面内的两条相交直线”是定理的关键点,一定要抓牢.但判定已知直线与平面垂直时,已知直线与平面内的直线可能为共面直线(相交),也可能为异面垂直(不相交).
如果一条直线垂直于一个平面内的:①三角形的两边; ②梯形的两边; ③圆的两条直径; ④正六边形的两边. 能保证该直线与平面垂直的是______.
根据直线与平面垂直的判定定理,平面内的这两条直线必须是相交的,而梯形的对边不一定相交,正六边形的对边也不相交,所以选①③
① ③
直线与平面所成的角
平面内一条斜线和它在平面上的射影所成的角,叫做这条直线和这个平面所成的角.
线面角θ的范围:0≤θ≤90°
?
图形语言:如图,∠PAO就是斜线AP与平面α所成的角.
?
????
?
????
?
????
?
????
?
????
?
垂线
斜线
射影
当直线与平面垂直时,∠ PAO=90°;
?
当直线与平面平行或在平面内时,
∠PAO=0°
?
探究新知
直线与平面所成的角
斜线在平面上的射影是过斜足和垂足的一条直线而不是线段;
P是斜线上异于斜足A的任意一点,点P具有任意性;
?
求一条直线与平面所成的角,可先作出直线在平面内的射影,从而得到直线与平面所成的角,再一步求解.
直线与平面所成的角的求解步骤
直线与平面所成的角
【证】证明所找到的角为直线与平面所成的角,其证明的主要依
据为直线与平面所成的角的定义
【作】在斜线上选取恰当的点向平面引垂线,在这一步,确定垂
足的位置是关键
【算】一般借助三角形的相关知识求解出线面角的大小
直线与平面垂直的性质定理
直线与平面垂直的性质定理①:垂直于平面的直线与平面内任意一条直线相互垂直.
图形语言:
符号语言:
????⊥α,b?α?????⊥b
?
????
?
????
?
????
?
定理应用:线面垂直?线线垂直
?
探究新知
直线与平面垂直的性质定理
直线与平面垂直的性质定理②:垂直于同一个平面的两条直线平行
图形语言:
符号语言:
????⊥α,b⊥α??????//?b
?
????
?
????
?
????
?
定理应用:①线面垂直?线线平行
②作平行线
?
垂直于同一个平面的
两个平面不一定平行
直线与平面垂直的性质定理
过一点作垂直于已知平面的直线,则该点与垂足之间的线段,叫做这个点到该平面的垂线段,出垂线段的长度叫做这个点到该平面的距离.
点面距AO的范围: AO≥0
?
图形语言:如图,线段AO的长度就是点A到平面α的距离.
当点A∈α时,????????=????,当A?α时, ????????>????
?
????
?
????
?
????
?
点到平面的距离
垂线
直线与平面垂直的性质定理
一条直线与一个平面平行时,这条直线上任意一点到这个平面的距离,叫做这条直线到这个平面的距离.
当直线 l 与平面 α?相交或 l?α 时,直线l到平面α的距离为0.
?
图形语言:如图,线段 AO 的长度就是直线????? 到平面 α 的距离.
?
????
?
????(垂足)
?
????
?
直线到平面的距离
垂线
????
?
????∈????
?
直线与平面垂直的性质定理
如果两个平面平行,那么其中一个平面内的任意一点到另一个平面的距离都相等. 我们把这个距离叫做两个平行平面之间的距离.
当平面?β 与平面 α?相交时,平面?β 到平面 α 的距离为0.
?
图形语言:如图,线段 AO 的长度就是平面?β 到平面 α 的距离.
?
????
?
????
?
????
?
平面到平面的距离
垂线
????∈????
?
????
?
点在平面内射影位置的确定
立体几何中经常遇到由一个点向一个平面做垂线的问题,垂线的位置由这个点在平面内的射影位置来确定,因此确定这个点的射影位置是解题关键.一般来说可以直接过这个点做平面的垂线,然后通过证明或计算说明垂足的位置,也可以借助以下常见结论进行确定——
经过一个角的顶点,引这个角所在平面的斜线,如果斜线与这个角的两边的夹角相等,那么该斜线在平面内的射影是这个角的平分线所在的直线
如果一个角所在平面外一点到角的两边距离相等,那么这一点在平面内的射影就是这个角的平分线所在的直线
点在平面内射影位置的确定
对于三棱锥A?BCD,有以下结论:
?
若????????=????????=????????,则点A在平面BCD内的射影为ΔBCD的外心;
?
若点????到????????,????????,????????的距离相等,且点????的射影在ΔBCD的内部,则点A在平面BCD内的射影为ΔBCD的内心;
?
若点????????⊥????????,????????⊥????????,则点A在平面BCD内的射影为ΔBCD的垂心
?
这些结论为确定点、斜线在平面内的射影的位置提供了重要的方法和依据,为分析问题时的广泛联想提供了有力的支持.
谢谢聆听
8.6.1-8.6.2 直线与直线
垂直、直线与平面垂直
????
?
????
?
????
?
????′
?
????
?
????
?
????
?
????
?
????
?
????????
?
????????
?
????????
?
????????
?
????
?
????
?
????
?
????
?
高中数学人教A版(2019)必修第二册
异面直线所成的角
已知两条异面直线a,b,经过空间任意一点O分别作直线a′//a, b′// b?,我们把直线a′与b′所成的角叫做异面直线a与b所成的角(或夹角).
?
异面直线所成角的概念
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????′
?
????
?
探究新知
异面直线所成的角
异面直线所成角的概念
异面直线所成的角的范围:由异面直线所成角的定义得,异面直线所成的角θ是锐角或者直角,即0°<θ ≤90°
研究异面直线所成的角,就是通过平移把异面直线转化为相交直线,把空间角问题转化为平面角问题,这是研究立体几何问题的一种基本思想,即空间问题平面化.
异面直线所成的角的大小不能是0°,当两条直线所成的角是0°时,这两条直线共面.
异面直线所成的角
如果两条异面直线所成的角是直角,我们就说这两条异面直线互相垂直.直线????与????直线垂直,记作????⊥????
?
两条异面直线垂直的定义
????
?
????
?
????
?
????
?
????
?
????
?
两条直线互相垂直,既包括相交垂直,也包括异面垂直.
异面直线所成的角
异面直线所成角的求解步骤
证明:证明作出的角就是要求解的角
构造:根据异面直线的定义,用平移法(常利用三角形中位线、平行四边形的性质)作出异面直线所成的角.
计算:求角度(常利用三角形的有关知识)
结论:若求出的角是锐角或者直角,则它就是所求异面直线所成的角;若求出的角是钝角,则它的补角就是所求异面直线所成的角.
异面直线所成的角
异面直线所成角的求解步骤
如图所示,已知正方体?????????????????????????????????????????????????,则异面直线????????????????与????????????所成的角的大小是多少?
?
????
?
????
?
????
?
????
?
????????
?
????????
?
????????
?
????????
?
连接????1????和????1????,∵ ????1????// ????1?????,
?
∴ ∠????1????1????为异面直线????1????1与????1????所成的角.
?
∵ ????1????,????1????1,????1????为正方体各面的对角线,
?
∴ ????1????=????1????1=????1????,∴ Δ????1????1????为正三角形,∴∠????1????1????=????????°
?
∴ 异面直线????1????1与????1????所成的角为60°.
?
直线与平面垂直
一般地,如果直线和平面内的任意一条直线都垂直,我们就说直线与平面互相垂直,记作⊥.直线叫做平面的垂线,平面叫做直线的垂面.直线与平面垂直时,它们唯一的公共点叫做垂足.
可以发现,过一点垂直于已知平面的直线有且只有一条.
直线与平面垂直是直线与平面相交的一种特殊情况.
定义中的“任意一条直线”与“所有直线”是同义词,但与“无数条直线”不同.定义的实质就是直线与平面内的所有直线都垂直.
运用直线与平面垂直的定义来判定直线与平面垂直时,要紧扣“一条直线与一个平面内的任意一条直线都垂直”这个条件.
探究新知
直线与平面垂直
图形语言:
符号语言:任意 ?????????,都有 ????⊥?????????⊥????
?
作图技巧:画直线 l 与平面 α 垂直时,通常把直线画成与表示平面的平行四边形的一边垂直
?
????
?
????
?
????
?
应用:
①若直线与平面垂直,则这条直线与这个平面内的所有直线都垂直,从而
可以判断直线与平面内的直线互相垂直,简述为“若线面垂直,则线线垂
直”.
②重要结论:过一点有且只有一条直线与已知平面垂直;
过一点有且只有一个平面与已知直线垂直.
直线与平面垂直的判定定理
如果一条直线与一个平面内的两条相交直线垂直,那么这条直线垂直于这个平面.
图形语言:
符号语言:
a?α,
b?α,
a∩b=????,
????⊥α,
????⊥b,
?
????⊥α?
?
????
?
????
?
????
?
????
?
定理应用:线线垂直?线面垂直
?
探究新知
直线与平面垂直的判定定理
判定定理的条件中“平面内的两条相交直线”是定理的关键点,一定要抓牢.但判定已知直线与平面垂直时,已知直线与平面内的直线可能为共面直线(相交),也可能为异面垂直(不相交).
如果一条直线垂直于一个平面内的:①三角形的两边; ②梯形的两边; ③圆的两条直径; ④正六边形的两边. 能保证该直线与平面垂直的是______.
根据直线与平面垂直的判定定理,平面内的这两条直线必须是相交的,而梯形的对边不一定相交,正六边形的对边也不相交,所以选①③
① ③
直线与平面所成的角
平面内一条斜线和它在平面上的射影所成的角,叫做这条直线和这个平面所成的角.
线面角θ的范围:0≤θ≤90°
?
图形语言:如图,∠PAO就是斜线AP与平面α所成的角.
?
????
?
????
?
????
?
????
?
????
?
垂线
斜线
射影
当直线与平面垂直时,∠ PAO=90°;
?
当直线与平面平行或在平面内时,
∠PAO=0°
?
探究新知
直线与平面所成的角
斜线在平面上的射影是过斜足和垂足的一条直线而不是线段;
P是斜线上异于斜足A的任意一点,点P具有任意性;
?
求一条直线与平面所成的角,可先作出直线在平面内的射影,从而得到直线与平面所成的角,再一步求解.
直线与平面所成的角的求解步骤
直线与平面所成的角
【证】证明所找到的角为直线与平面所成的角,其证明的主要依
据为直线与平面所成的角的定义
【作】在斜线上选取恰当的点向平面引垂线,在这一步,确定垂
足的位置是关键
【算】一般借助三角形的相关知识求解出线面角的大小
直线与平面垂直的性质定理
直线与平面垂直的性质定理①:垂直于平面的直线与平面内任意一条直线相互垂直.
图形语言:
符号语言:
????⊥α,b?α?????⊥b
?
????
?
????
?
????
?
定理应用:线面垂直?线线垂直
?
探究新知
直线与平面垂直的性质定理
直线与平面垂直的性质定理②:垂直于同一个平面的两条直线平行
图形语言:
符号语言:
????⊥α,b⊥α??????//?b
?
????
?
????
?
????
?
定理应用:①线面垂直?线线平行
②作平行线
?
垂直于同一个平面的
两个平面不一定平行
直线与平面垂直的性质定理
过一点作垂直于已知平面的直线,则该点与垂足之间的线段,叫做这个点到该平面的垂线段,出垂线段的长度叫做这个点到该平面的距离.
点面距AO的范围: AO≥0
?
图形语言:如图,线段AO的长度就是点A到平面α的距离.
当点A∈α时,????????=????,当A?α时, ????????>????
?
????
?
????
?
????
?
点到平面的距离
垂线
直线与平面垂直的性质定理
一条直线与一个平面平行时,这条直线上任意一点到这个平面的距离,叫做这条直线到这个平面的距离.
当直线 l 与平面 α?相交或 l?α 时,直线l到平面α的距离为0.
?
图形语言:如图,线段 AO 的长度就是直线????? 到平面 α 的距离.
?
????
?
????(垂足)
?
????
?
直线到平面的距离
垂线
????
?
????∈????
?
直线与平面垂直的性质定理
如果两个平面平行,那么其中一个平面内的任意一点到另一个平面的距离都相等. 我们把这个距离叫做两个平行平面之间的距离.
当平面?β 与平面 α?相交时,平面?β 到平面 α 的距离为0.
?
图形语言:如图,线段 AO 的长度就是平面?β 到平面 α 的距离.
?
????
?
????
?
????
?
平面到平面的距离
垂线
????∈????
?
????
?
点在平面内射影位置的确定
立体几何中经常遇到由一个点向一个平面做垂线的问题,垂线的位置由这个点在平面内的射影位置来确定,因此确定这个点的射影位置是解题关键.一般来说可以直接过这个点做平面的垂线,然后通过证明或计算说明垂足的位置,也可以借助以下常见结论进行确定——
经过一个角的顶点,引这个角所在平面的斜线,如果斜线与这个角的两边的夹角相等,那么该斜线在平面内的射影是这个角的平分线所在的直线
如果一个角所在平面外一点到角的两边距离相等,那么这一点在平面内的射影就是这个角的平分线所在的直线
点在平面内射影位置的确定
对于三棱锥A?BCD,有以下结论:
?
若????????=????????=????????,则点A在平面BCD内的射影为ΔBCD的外心;
?
若点????到????????,????????,????????的距离相等,且点????的射影在ΔBCD的内部,则点A在平面BCD内的射影为ΔBCD的内心;
?
若点????????⊥????????,????????⊥????????,则点A在平面BCD内的射影为ΔBCD的垂心
?
这些结论为确定点、斜线在平面内的射影的位置提供了重要的方法和依据,为分析问题时的广泛联想提供了有力的支持.
谢谢聆听
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
