变化率问题
图片预览







文档简介
(共23张PPT)
法国《队报》网站的文章称刘翔以不可思议的速度统治
了赛场。这名21岁的中国人跑的几乎比炮弹还快,赛道
上显示的12.94秒的成绩已经打破了12.95奥运会记录,但
经过验证他是以12.91秒平了世界纪录,他的平均速度
达到8.52m/s。
平均速度的数学意义是什么
如何求瞬时速度呢?
微积分主要与四类问题的处理相关:
一、已知物体运动的路程作为时间的函数,求物
体在任意时刻的速度与加速度等;
二、求曲线的切线;
三、求已知函数的最大值与最小值;
四、求长度、面积、体积和重心等。
导数是微积分的核心概念之一它是研究函数增减、变化快慢、最大(小)值等问题最一般、最有效的工具。
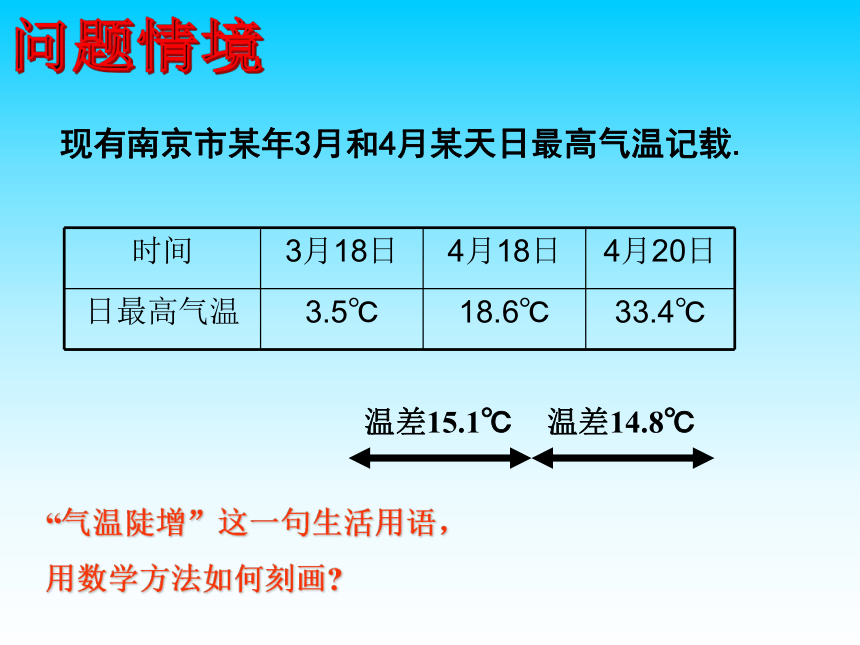
现有南京市某年3月和4月某天日最高气温记载.
时间 3月18日 4月18日 4月20日
日最高气温 3.5℃ 18.6℃ 33.4℃
“气温陡增”这一句生活用语,
用数学方法如何刻画
温差15.1℃
温差14.8℃
t(d)
20
30
34
2
10
20
30
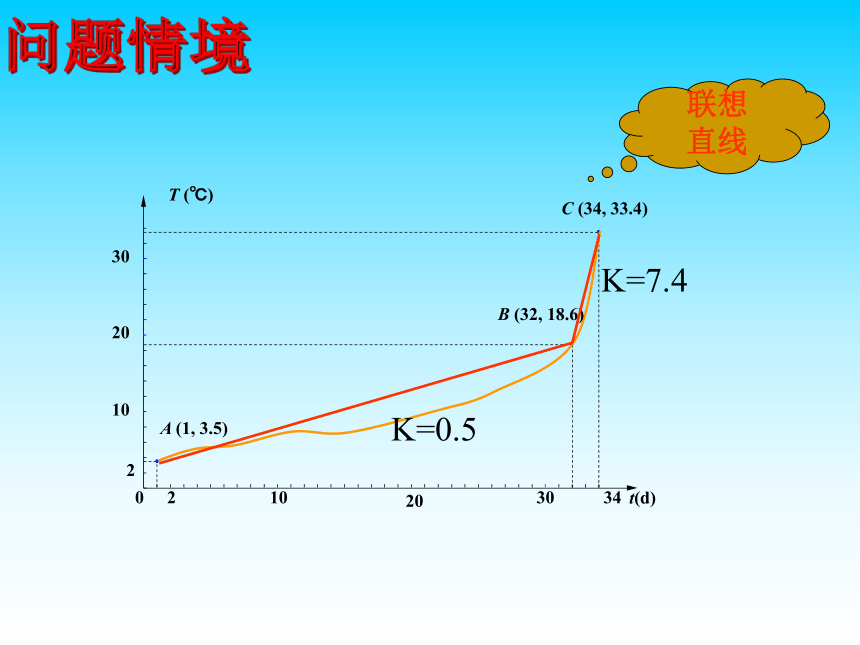
A (1, 3.5)
B (32, 18.6)
0
C (34, 33.4)
T (℃)
2
10
联想
直线
K=7.4
K=0.5
问题1:气球膨胀率
很多人都吹过气球,回忆一下吹气球的过程
随着气球内空气容量的增加,气球的半径增加的越来越慢。
从数学的角度,如何描述这种现象呢?
发现:
当空气容量V从0增加1L时,半径增加了
r(1)-r(0)≈ 0.62 (dm)
气球的平均膨胀率为:
气球的体积V(单位:L)与半径r(单位:dm)之间的函数关系是:
类似地:
当空气容量V从1加2L时,半径增加了
r(2)-r(1) ≈ 0.16(dm)
气球的平均膨胀率为:
可以看出:
随着气球体积逐渐变大,它的平均膨胀率逐渐变小。
思考?
当空气容量从V1增加到V2时,气球的平均膨胀率是多少?
问题2:高台跳水
在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:s)存在函数关系h(t)= - 4.9 t2+ 6.5t +10.
如果我们用运动员在某段时间内的平均速度 描述其运动状态,那么:
在1秒到2秒时间段内呢?
运动员在0秒到0.5秒时间段内的平均速度是多少?
探究
计算:运动员在
这段时间内的平均速度,并思考下面的问题:
(2)你认为用平均速度描述运动员的运动状态有什么问题吗?
平均速度不能反映他在这段时间里运动状态,
需要用瞬时速度描述运动状态。
(1)运动员在这段
时间里是静止的吗?
气球的平均膨胀率是一个特殊的情况,我们把这一思路延伸到函数上,归纳一下得出函数的平均变化率
探究活动
从以上的二个例子中,我们可以了解到,平均变化率是指在某个区间内数值的平均变化量.
如果上述两个问题中的函数关系用 表示,
那么问题中的变化率可用式子:
“增量”:
令“增量”
于是:平均变化率可以表示为:
理解:
式子中△x 、△ y的值可正、可负,
但△x的值不能为0, △ y的值可以为0
若函数f (x)为常函数时, △ y=0
思考
观察函数f(x)的图象
平均变化率 表示什么
O
A
B
x
y
Y=f(x)
x1
x2
f(x1)
f(x2)
x2-x1=△x
f(x2)-f(x1)=△y
直线AB的
斜率
1.函数的平均变化率
小结:
2.求函数的平均变化率的步骤:
(1)求函数的增量:Δy=f(x2)-f(x1)
(2)计算平均变化率
法国《队报》网站的文章称刘翔以不可思议的速度统治
了赛场。这名21岁的中国人跑的几乎比炮弹还快,赛道
上显示的12.94秒的成绩已经打破了12.95奥运会记录,但
经过验证他是以12.91秒平了世界纪录,他的平均速度
达到8.52m/s。
平均速度的数学意义是什么
如何求瞬时速度呢?
微积分主要与四类问题的处理相关:
一、已知物体运动的路程作为时间的函数,求物
体在任意时刻的速度与加速度等;
二、求曲线的切线;
三、求已知函数的最大值与最小值;
四、求长度、面积、体积和重心等。
导数是微积分的核心概念之一它是研究函数增减、变化快慢、最大(小)值等问题最一般、最有效的工具。
现有南京市某年3月和4月某天日最高气温记载.
时间 3月18日 4月18日 4月20日
日最高气温 3.5℃ 18.6℃ 33.4℃
“气温陡增”这一句生活用语,
用数学方法如何刻画
温差15.1℃
温差14.8℃
t(d)
20
30
34
2
10
20
30
A (1, 3.5)
B (32, 18.6)
0
C (34, 33.4)
T (℃)
2
10
联想
直线
K=7.4
K=0.5
问题1:气球膨胀率
很多人都吹过气球,回忆一下吹气球的过程
随着气球内空气容量的增加,气球的半径增加的越来越慢。
从数学的角度,如何描述这种现象呢?
发现:
当空气容量V从0增加1L时,半径增加了
r(1)-r(0)≈ 0.62 (dm)
气球的平均膨胀率为:
气球的体积V(单位:L)与半径r(单位:dm)之间的函数关系是:
类似地:
当空气容量V从1加2L时,半径增加了
r(2)-r(1) ≈ 0.16(dm)
气球的平均膨胀率为:
可以看出:
随着气球体积逐渐变大,它的平均膨胀率逐渐变小。
思考?
当空气容量从V1增加到V2时,气球的平均膨胀率是多少?
问题2:高台跳水
在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:s)存在函数关系h(t)= - 4.9 t2+ 6.5t +10.
如果我们用运动员在某段时间内的平均速度 描述其运动状态,那么:
在1秒到2秒时间段内呢?
运动员在0秒到0.5秒时间段内的平均速度是多少?
探究
计算:运动员在
这段时间内的平均速度,并思考下面的问题:
(2)你认为用平均速度描述运动员的运动状态有什么问题吗?
平均速度不能反映他在这段时间里运动状态,
需要用瞬时速度描述运动状态。
(1)运动员在这段
时间里是静止的吗?
气球的平均膨胀率是一个特殊的情况,我们把这一思路延伸到函数上,归纳一下得出函数的平均变化率
探究活动
从以上的二个例子中,我们可以了解到,平均变化率是指在某个区间内数值的平均变化量.
如果上述两个问题中的函数关系用 表示,
那么问题中的变化率可用式子:
“增量”:
令“增量”
于是:平均变化率可以表示为:
理解:
式子中△x 、△ y的值可正、可负,
但△x的值不能为0, △ y的值可以为0
若函数f (x)为常函数时, △ y=0
思考
观察函数f(x)的图象
平均变化率 表示什么
O
A
B
x
y
Y=f(x)
x1
x2
f(x1)
f(x2)
x2-x1=△x
f(x2)-f(x1)=△y
直线AB的
斜率
1.函数的平均变化率
小结:
2.求函数的平均变化率的步骤:
(1)求函数的增量:Δy=f(x2)-f(x1)
(2)计算平均变化率
