8.3 动能和动能定理 同步练习—2020-2021学年【新教材】人教版(2019)高中物理必修第二册(word含答案)
文档属性
| 名称 | 8.3 动能和动能定理 同步练习—2020-2021学年【新教材】人教版(2019)高中物理必修第二册(word含答案) | 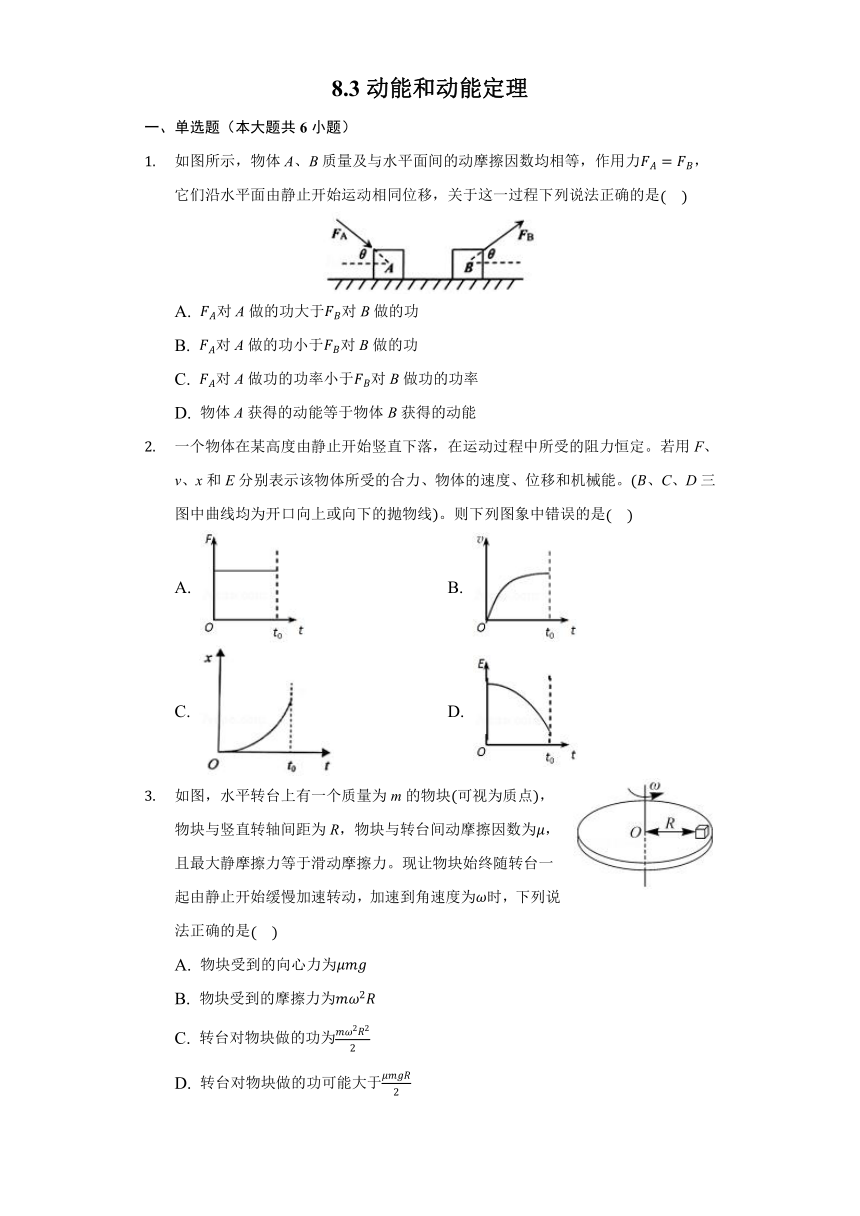 | |
| 格式 | docx | ||
| 文件大小 | 101.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-05-05 15:06:01 | ||
图片预览



文档简介
8.3动能和动能定理
一、单选题(本大题共6小题)
如图所示,物体A、B质量及与水平面间的动摩擦因数均相等,作用力FA=FB,它们沿水平面由静止开始运动相同位移,关于这一过程下列说法正确的是(????)
A. FA对A做的功大于FB对B做的功
B. FA对A做的功小于FB对B做的功
C. FA对A做功的功率小于FB对B做功的功率
D. 物体A获得的动能等于物体B获得的动能
一个物体在某高度由静止开始竖直下落,在运动过程中所受的阻力恒定。若用F、v、x和E分别表示该物体所受的合力、物体的速度、位移和机械能。(B、C、D三图中曲线均为开口向上或向下的抛物线)。则下列图象中错误的是(????)
A. B.
C. D.
如图,水平转台上有一个质量为m的物块(可视为质点),物块与竖直转轴间距为R,物块与转台间动摩擦因数为μ,且最大静摩擦力等于滑动摩擦力。现让物块始终随转台一起由静止开始缓慢加速转动,加速到角速度为ω时,下列说法正确的是(????)
A. 物块受到的向心力为μmg
B. 物块受到的摩擦力为mω2R
C. 转台对物块做的功为mω2R22
D. 转台对物块做的功可能大于μmgR2
如图所示,用长为l的轻质细线悬挂一个质量未知的小球,小球在A位置静止。现用力缓慢将小球拉到B位置,在这一过程中拉力做功为WF,细线与竖直方向的夹角为θ,当地重力加速度为g,则小球质量为(????)
A. WFgl1?cosθ B. WFglcosθ C. WFgltanθ D. WFglsinθ
某景点的滑草场有两个坡度不同的滑道AB和AB?(均可看作斜面),甲、乙两名质量相等的游客分别乘两个完全相同的滑草装置从A点由静止开始分别沿AB和AB?滑下,最后都停在水平草面上,其中乙停在了C点处,如图所示。设滑草装置和草面间的动摩擦因数处处相同,斜面与水平面连接处均可认为是圆滑的,滑草者保持相同的姿势坐在滑草装置上不动,则甲最终停在了(????)
A. C点的左侧 B. 正好C点处
C. C点的右侧 D. 条件不足,无法判断
如图所示,粗糙的固定水平杆上有A、B、C三点,轻质弹簧一端固定在B点正下方的O点,另一端与套在杆A点、质量为m的圆环相连,此时弹簧处于拉伸状态。圆环从A处由静止释放,向右运动经过B点时速度为v、加速度为零,到达C点时速度为零,下列说法正确的是(????)
A. 从A到C过程中,圆环在B点速度最大
B. 从A到C过程中,圆环的加速度先减小后增大
C. 从A到B过程中,弹簧对圆环做的功一定大于12mv2
D. 从B到C过程中,圆环克服摩擦力做功等于12mv2
二、填空题(本大题共2小题)
如图,倾角为θ的固定斜面上AB段光滑,BC段粗糙,且BC=2AB.若P由静止开始从A点释放,恰好能滑动到C点而停下,则小物块P与BC段斜面之间的动摩擦因数μ=_________;若P以初速度v0从A点开始运动,则到达C点时的速度vC______v0(选填“>”、“<”或“=”)。
如图所示,细线长为L,悬挂一质量为m的小球静止在A点。今施加在小球上一个水平向右的恒力F使其运动到B点,此时细线与竖直方向夹角为θ,重力加速度为g,小球可视为质点。那么在这一过程中,恒力对小球做的功为____,小球在B处时动能为____。
三、计算题(本大题共2小题)
如图所示,竖直平面内一倾角为θ=37°的粗糙倾斜直轨道AB与光滑圆弧轨道BC相切于B点,圆弧轨道与传送带水平段平顺连接于C点。一质量为m=200g的小滑块从A点静止释放,经B点最后从C点水平滑上传送带。已知A点离地高度为H=1.15m,AB长L1=1.0m,滑块与AB间的动摩擦因数为μ1=0.25,与传送带间的动摩擦因数为μ2=0.20,CD长度为L2=3.0m,圆弧轨道半径为R=0.5m。若滑块可视为质点,全程不计空气阻力,求:
(1)小滑块经过C点时对轨道的压力;
(2)当传送带以顺时针方向v1=4.0m/s的速度转动时,小滑块从水平传送带右端D点水平抛出后,落地点到D点的水平距离;
(3)若传送带以逆时针方向v2=2.0m/s的速度转动,则小滑块在倾斜直轨道上运动的总路程为多少?
如图甲所示,粗糙水平轨道与半径为R的竖直光滑、绝缘的半圆轨道在B点平滑连接,过半圆轨道圆心O的水平界面MN的下方分布有水平向右的匀强电场E,质量为m的带正电小滑块从水平轨道上A点由静止释放,运动中由于摩擦起电滑块电荷量会增加,过B点后电荷量保持不变,小滑块在AB段加速度随位移变化图象如图乙所示。已知A、B间距离为4R,滑块与轨道间动摩擦因数为μ=0.5,重力加速度为g,不计空气阻力,求:
(1)小滑块释放后运动至B点过程中电荷量的变化量;
(2)滑块对半圆轨道的最大压力大小。
答案和解析
1. C2. B3. C4. A5.B6. C
7. 3tanθ2;=。
8. FLsinθ;FLsinθ?mgL(1?cosθ)?。
9.解:(1)对小滑块从A至C过程,
应用动能定理得mgL1?sinθ+R1?cosθ?μmgL1?cosθ=12mvC2?0,
解得:vC=10m/s
小滑块经过C点时,据牛顿第二定律得?F支?mg=mvC2R,解得:F支=6N
据牛顿第三定律可得滑块在C点对轨道的压力F压=F支=6N,方向竖直向下;
(2)若传送带上全程加速,据牛顿第二定律得μ2mg=ma,解得滑块的加速度a=2m/s2
据速度?位移关系公式可得:vD2?vC2=2aL2,解得:vD=22m/s>v1=4m/s
故小滑块以传送带速度平抛,在竖直方向上有H?L1?sinθ?R1?cosθ=12gt2,
解得:t=0.3s
水平方向上,有x=v1t=1.2m
(3)小滑块第1次滑上传送带后,以传送带速度2.0m/s返回C点,通过圆弧轨道滑上斜面然后滑下,如此往复后最终小滑块运动至B点时速度接近0,
故研究第1次返回C点至最终状态,
据动能定理可得?mgR(1?cosθ)?μ1mgcosθ?S=0?12mv22,解得:S=0.5m
所以小滑块通过斜面AB的总路程为S'=S+AB=0.5m+1m=1.5m
答:(1)小滑块经过C点时对轨道的压力为6N;
(2)当传送带以顺时针方向v1=4.0m/s的速度转动时,小滑块从水平传送带右端D点水平抛出后,落地点到D点的水平距离为1.2m;
(3)若传送带以逆时针方向v2=2.0m/s的速度转动,则小滑块在倾斜直轨道上运动的总路程为1.5m;
10.解:(1)A点由牛顿第二定律可得:q0E?μmg=12mg①
B点由牛顿第二定律可得:q1E?μmg=32mg②
Δq=q1?q0③
联立①②③可得:Δq=mgE;
(2)小滑块由A到B由动能定理得m12g+32g2?4R=12mv12?0④
将电场力与重力等效为“重力G'”,与竖直方向的夹角设为α,在“等效最低点”对轨道压力最大,则G'=mg2+q1E2=5mg⑤
cosα=mgG'⑥
小滑块从B到“等效最低点”由动能定理得G'R+Rcosα=12m22?12m12⑦
小滑块在“等效最低点”时,由牛顿第二定律可得FN?G'=mv22R⑧
由牛顿第三定律得滑块对圆轨道的最大压力为FN'=FN⑨
联立④⑤⑥⑦⑧⑨可得FN'=6+35mg。
答:(1)小滑块释放后运动至B点过程中电荷量的变化量为mgE;
(2)滑块对半圆轨道的最大压力大小为6+35mg。
【解析】略
一、单选题(本大题共6小题)
如图所示,物体A、B质量及与水平面间的动摩擦因数均相等,作用力FA=FB,它们沿水平面由静止开始运动相同位移,关于这一过程下列说法正确的是(????)
A. FA对A做的功大于FB对B做的功
B. FA对A做的功小于FB对B做的功
C. FA对A做功的功率小于FB对B做功的功率
D. 物体A获得的动能等于物体B获得的动能
一个物体在某高度由静止开始竖直下落,在运动过程中所受的阻力恒定。若用F、v、x和E分别表示该物体所受的合力、物体的速度、位移和机械能。(B、C、D三图中曲线均为开口向上或向下的抛物线)。则下列图象中错误的是(????)
A. B.
C. D.
如图,水平转台上有一个质量为m的物块(可视为质点),物块与竖直转轴间距为R,物块与转台间动摩擦因数为μ,且最大静摩擦力等于滑动摩擦力。现让物块始终随转台一起由静止开始缓慢加速转动,加速到角速度为ω时,下列说法正确的是(????)
A. 物块受到的向心力为μmg
B. 物块受到的摩擦力为mω2R
C. 转台对物块做的功为mω2R22
D. 转台对物块做的功可能大于μmgR2
如图所示,用长为l的轻质细线悬挂一个质量未知的小球,小球在A位置静止。现用力缓慢将小球拉到B位置,在这一过程中拉力做功为WF,细线与竖直方向的夹角为θ,当地重力加速度为g,则小球质量为(????)
A. WFgl1?cosθ B. WFglcosθ C. WFgltanθ D. WFglsinθ
某景点的滑草场有两个坡度不同的滑道AB和AB?(均可看作斜面),甲、乙两名质量相等的游客分别乘两个完全相同的滑草装置从A点由静止开始分别沿AB和AB?滑下,最后都停在水平草面上,其中乙停在了C点处,如图所示。设滑草装置和草面间的动摩擦因数处处相同,斜面与水平面连接处均可认为是圆滑的,滑草者保持相同的姿势坐在滑草装置上不动,则甲最终停在了(????)
A. C点的左侧 B. 正好C点处
C. C点的右侧 D. 条件不足,无法判断
如图所示,粗糙的固定水平杆上有A、B、C三点,轻质弹簧一端固定在B点正下方的O点,另一端与套在杆A点、质量为m的圆环相连,此时弹簧处于拉伸状态。圆环从A处由静止释放,向右运动经过B点时速度为v、加速度为零,到达C点时速度为零,下列说法正确的是(????)
A. 从A到C过程中,圆环在B点速度最大
B. 从A到C过程中,圆环的加速度先减小后增大
C. 从A到B过程中,弹簧对圆环做的功一定大于12mv2
D. 从B到C过程中,圆环克服摩擦力做功等于12mv2
二、填空题(本大题共2小题)
如图,倾角为θ的固定斜面上AB段光滑,BC段粗糙,且BC=2AB.若P由静止开始从A点释放,恰好能滑动到C点而停下,则小物块P与BC段斜面之间的动摩擦因数μ=_________;若P以初速度v0从A点开始运动,则到达C点时的速度vC______v0(选填“>”、“<”或“=”)。
如图所示,细线长为L,悬挂一质量为m的小球静止在A点。今施加在小球上一个水平向右的恒力F使其运动到B点,此时细线与竖直方向夹角为θ,重力加速度为g,小球可视为质点。那么在这一过程中,恒力对小球做的功为____,小球在B处时动能为____。
三、计算题(本大题共2小题)
如图所示,竖直平面内一倾角为θ=37°的粗糙倾斜直轨道AB与光滑圆弧轨道BC相切于B点,圆弧轨道与传送带水平段平顺连接于C点。一质量为m=200g的小滑块从A点静止释放,经B点最后从C点水平滑上传送带。已知A点离地高度为H=1.15m,AB长L1=1.0m,滑块与AB间的动摩擦因数为μ1=0.25,与传送带间的动摩擦因数为μ2=0.20,CD长度为L2=3.0m,圆弧轨道半径为R=0.5m。若滑块可视为质点,全程不计空气阻力,求:
(1)小滑块经过C点时对轨道的压力;
(2)当传送带以顺时针方向v1=4.0m/s的速度转动时,小滑块从水平传送带右端D点水平抛出后,落地点到D点的水平距离;
(3)若传送带以逆时针方向v2=2.0m/s的速度转动,则小滑块在倾斜直轨道上运动的总路程为多少?
如图甲所示,粗糙水平轨道与半径为R的竖直光滑、绝缘的半圆轨道在B点平滑连接,过半圆轨道圆心O的水平界面MN的下方分布有水平向右的匀强电场E,质量为m的带正电小滑块从水平轨道上A点由静止释放,运动中由于摩擦起电滑块电荷量会增加,过B点后电荷量保持不变,小滑块在AB段加速度随位移变化图象如图乙所示。已知A、B间距离为4R,滑块与轨道间动摩擦因数为μ=0.5,重力加速度为g,不计空气阻力,求:
(1)小滑块释放后运动至B点过程中电荷量的变化量;
(2)滑块对半圆轨道的最大压力大小。
答案和解析
1. C2. B3. C4. A5.B6. C
7. 3tanθ2;=。
8. FLsinθ;FLsinθ?mgL(1?cosθ)?。
9.解:(1)对小滑块从A至C过程,
应用动能定理得mgL1?sinθ+R1?cosθ?μmgL1?cosθ=12mvC2?0,
解得:vC=10m/s
小滑块经过C点时,据牛顿第二定律得?F支?mg=mvC2R,解得:F支=6N
据牛顿第三定律可得滑块在C点对轨道的压力F压=F支=6N,方向竖直向下;
(2)若传送带上全程加速,据牛顿第二定律得μ2mg=ma,解得滑块的加速度a=2m/s2
据速度?位移关系公式可得:vD2?vC2=2aL2,解得:vD=22m/s>v1=4m/s
故小滑块以传送带速度平抛,在竖直方向上有H?L1?sinθ?R1?cosθ=12gt2,
解得:t=0.3s
水平方向上,有x=v1t=1.2m
(3)小滑块第1次滑上传送带后,以传送带速度2.0m/s返回C点,通过圆弧轨道滑上斜面然后滑下,如此往复后最终小滑块运动至B点时速度接近0,
故研究第1次返回C点至最终状态,
据动能定理可得?mgR(1?cosθ)?μ1mgcosθ?S=0?12mv22,解得:S=0.5m
所以小滑块通过斜面AB的总路程为S'=S+AB=0.5m+1m=1.5m
答:(1)小滑块经过C点时对轨道的压力为6N;
(2)当传送带以顺时针方向v1=4.0m/s的速度转动时,小滑块从水平传送带右端D点水平抛出后,落地点到D点的水平距离为1.2m;
(3)若传送带以逆时针方向v2=2.0m/s的速度转动,则小滑块在倾斜直轨道上运动的总路程为1.5m;
10.解:(1)A点由牛顿第二定律可得:q0E?μmg=12mg①
B点由牛顿第二定律可得:q1E?μmg=32mg②
Δq=q1?q0③
联立①②③可得:Δq=mgE;
(2)小滑块由A到B由动能定理得m12g+32g2?4R=12mv12?0④
将电场力与重力等效为“重力G'”,与竖直方向的夹角设为α,在“等效最低点”对轨道压力最大,则G'=mg2+q1E2=5mg⑤
cosα=mgG'⑥
小滑块从B到“等效最低点”由动能定理得G'R+Rcosα=12m22?12m12⑦
小滑块在“等效最低点”时,由牛顿第二定律可得FN?G'=mv22R⑧
由牛顿第三定律得滑块对圆轨道的最大压力为FN'=FN⑨
联立④⑤⑥⑦⑧⑨可得FN'=6+35mg。
答:(1)小滑块释放后运动至B点过程中电荷量的变化量为mgE;
(2)滑块对半圆轨道的最大压力大小为6+35mg。
【解析】略
