导数的几何意义
图片预览


文档简介
(共26张PPT)
3.1.3导数的几何意义
回顾
①导数的概念
函数 y = f (x) 在 x = x0 处的瞬时变化率
称为函数 y = f (x) 在 x = x0 处的导数, 记作
或 , 即
导数是“平均变化率的极限”
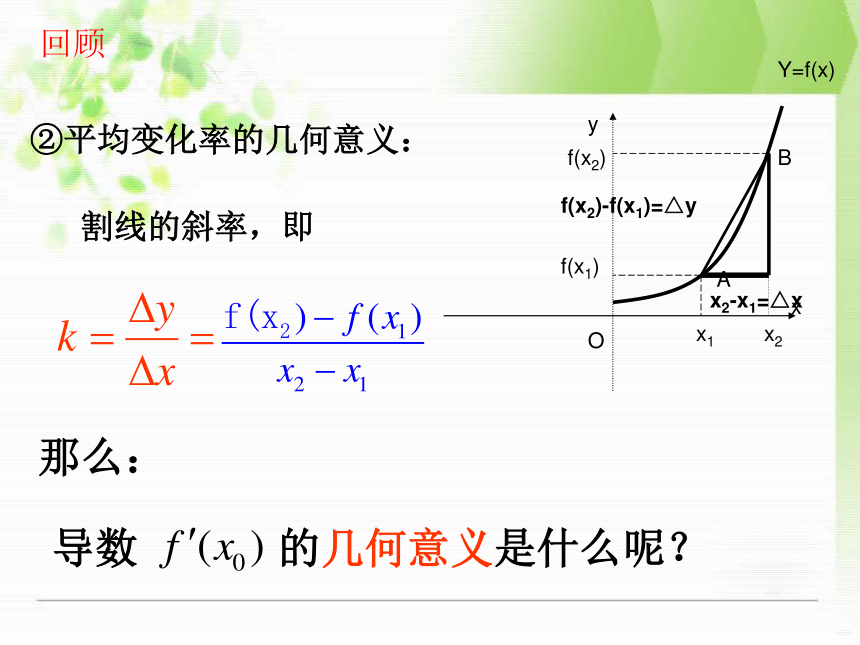
②平均变化率的几何意义:
O
A
B
x
y
Y=f(x)
x1
x2
f(x1)
f(x2)
x2-x1=△x
f(x2)-f(x1)=△y
割线的斜率,即
回顾
那么:
导数 的几何意义是什么呢?
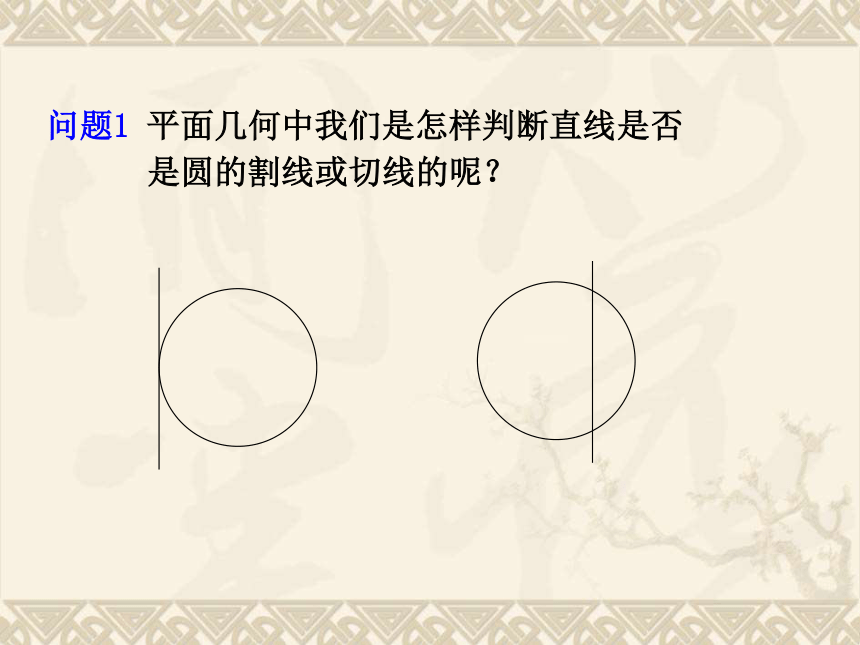
问题1 平面几何中我们是怎样判断直线是否
是圆的割线或切线的呢?
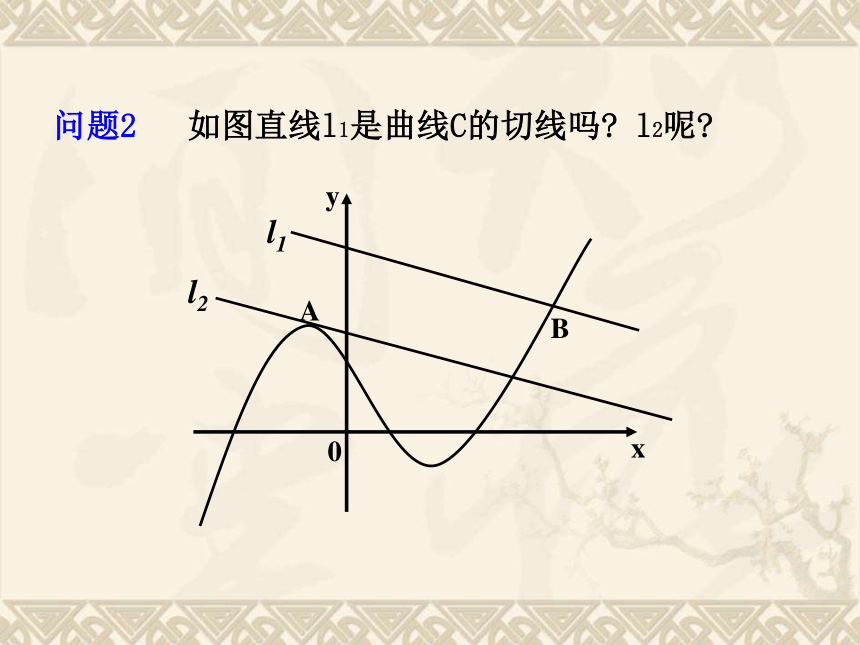
问题2 如图直线l1是曲线C的切线吗 l2呢
l2
l1
A
B
0
x
y
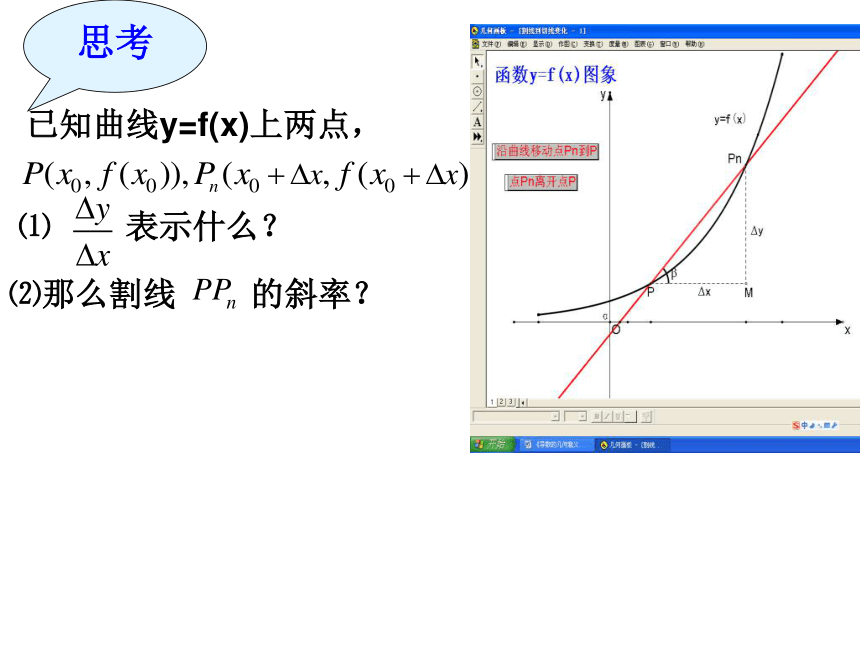
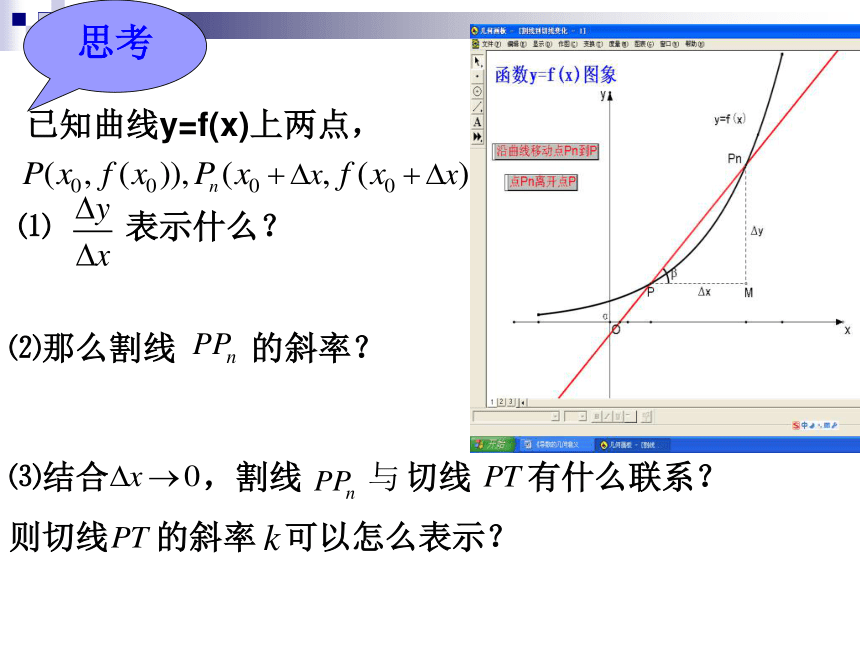
⑴ 表示什么?
思考
已知曲线y=f(x)上两点,
⑵那么割线 的斜率?
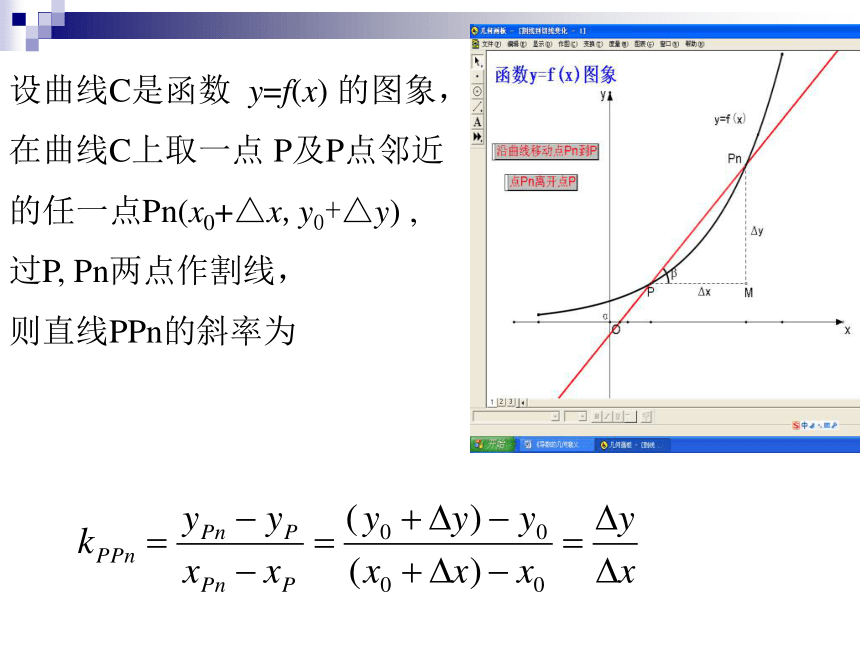
设曲线C是函数 y=f(x) 的图象,
在曲线C上取一点 P及P点邻近
的任一点Pn(x0+△x,y0+△y) ,
过P, Pn两点作割线,
则直线PPn的斜率为
⑴ 表示什么?
思考
已知曲线y=f(x)上两点,
⑶结合 ,割线 切线 有什么联系?
则切线 的斜率 可以怎么表示?
⑵那么割线 的斜率?
与
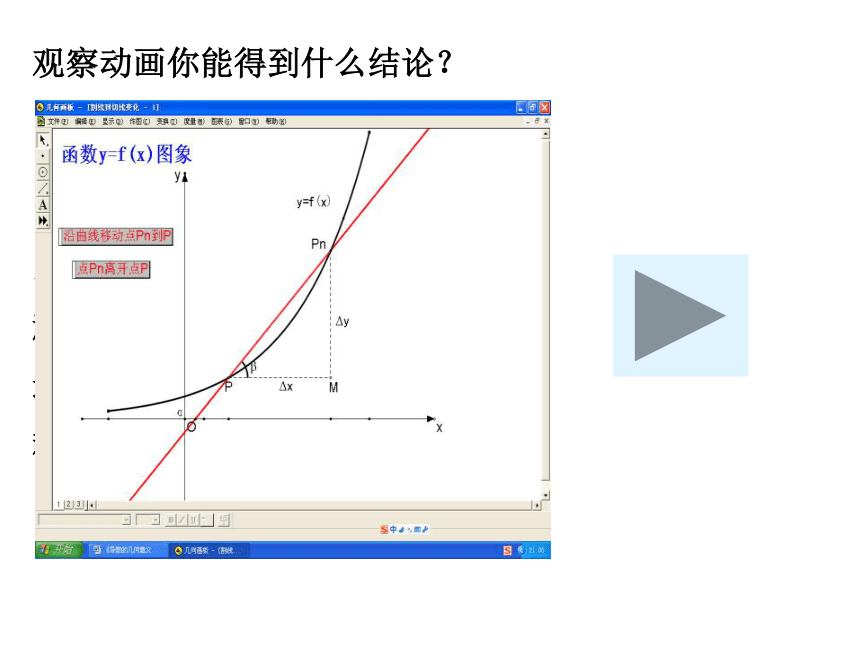
观察动画你能得到什么结论?
切线的定义:
当点 沿着曲线逼近
点 时,即 ,割线
趋近于一个极限位置,
这个极限位置上的直线PT
称为点P处的切线。
当Pn逐渐向P靠近时,
也即△x 逐渐变小。
当△x→0时,PPn无限靠近PT
因此:
切线的定义:
当点 沿着曲线逼近
点 时,即 ,割线
趋近于一个极限位置,
这个极限位置上的直线PT
称为点P处的切线。
在上面的研究过程中,某点的割线斜率和切线斜率与某点附近的平均变化率和某点的瞬时变化率有何联系?
平均变化率
割线的斜率
瞬时变化率(导数)
切线的斜率
导数的几何意义:
应用:
Q
P
y
=
x
2
+1
x
y
-
1
1
1
O
j
M
D
y
D
x
例1:
已知曲线 ,求在点p(1,2)处的切线方程.
解:
故,切线方程为:
即:
求曲线在某点处的切线方程的基本步骤:
①求出P点的坐标;
②利用切线斜率的定义求
出切线的斜率;
③利用点斜式求切线方程.
例2 如图, 它表示跳水运动中高度随时间变化的函数
的图象. 根据图象, 请描述、比较
曲线 在 附近的变化情况.
t
o
h
t0
t1
t2
l0
l1
l2
t4
t3
例2
解:可用曲线 h(t) 在 t0 , t1 , t2 处的切线刻画曲线 h(t) 在上述三个时刻附近的变化情况.
(1)当 t = t0 时, 曲线 h(t) 在 t0 处的切线 l0 平行于 x 轴.故在 t = t0 附近曲线比较平坦, 几乎没有升降.
(2)当 t = t1 时, 曲线 h(t) 在 t1 处的切线 l1 的斜率 h’(t1) <0 .故在t = t1 附近曲线下降,即函数 h(t) 在 t = t1 附近单调递减.
t
o
h
l0
t0
t1
l1
t2
l2
t4
t3
(3)当 t = t2 时, 曲线 h(t) 在 t2处的切线 l2 的斜率 h’(t2) <0 .故在 t = t2 附近曲线下降,即函数 h(t) 在t = t2 附近也单调递减.
从图可以看出,直线 l1 的倾斜程度小于直线 l2 的倾斜程度,这说明 h(t) 曲线在 l1 附近比在 l2 附近下降得缓慢
归纳小结
通过观察跳水问题中导数的变化情况,你得到了哪些结论
(1)函数的单调性与其导函数正负的关系 ;
(2)曲线的变化快慢及切线的倾斜程度的内在联系 .
练习:课本80页 B3
从求函数f(x)在x=x0处导数的过程可以看到:当x=x0时, 是一个确定的数。
即:
思考
思考解答
3.1.3导数的几何意义
回顾
①导数的概念
函数 y = f (x) 在 x = x0 处的瞬时变化率
称为函数 y = f (x) 在 x = x0 处的导数, 记作
或 , 即
导数是“平均变化率的极限”
②平均变化率的几何意义:
O
A
B
x
y
Y=f(x)
x1
x2
f(x1)
f(x2)
x2-x1=△x
f(x2)-f(x1)=△y
割线的斜率,即
回顾
那么:
导数 的几何意义是什么呢?
问题1 平面几何中我们是怎样判断直线是否
是圆的割线或切线的呢?
问题2 如图直线l1是曲线C的切线吗 l2呢
l2
l1
A
B
0
x
y
⑴ 表示什么?
思考
已知曲线y=f(x)上两点,
⑵那么割线 的斜率?
设曲线C是函数 y=f(x) 的图象,
在曲线C上取一点 P及P点邻近
的任一点Pn(x0+△x,y0+△y) ,
过P, Pn两点作割线,
则直线PPn的斜率为
⑴ 表示什么?
思考
已知曲线y=f(x)上两点,
⑶结合 ,割线 切线 有什么联系?
则切线 的斜率 可以怎么表示?
⑵那么割线 的斜率?
与
观察动画你能得到什么结论?
切线的定义:
当点 沿着曲线逼近
点 时,即 ,割线
趋近于一个极限位置,
这个极限位置上的直线PT
称为点P处的切线。
当Pn逐渐向P靠近时,
也即△x 逐渐变小。
当△x→0时,PPn无限靠近PT
因此:
切线的定义:
当点 沿着曲线逼近
点 时,即 ,割线
趋近于一个极限位置,
这个极限位置上的直线PT
称为点P处的切线。
在上面的研究过程中,某点的割线斜率和切线斜率与某点附近的平均变化率和某点的瞬时变化率有何联系?
平均变化率
割线的斜率
瞬时变化率(导数)
切线的斜率
导数的几何意义:
应用:
Q
P
y
=
x
2
+1
x
y
-
1
1
1
O
j
M
D
y
D
x
例1:
已知曲线 ,求在点p(1,2)处的切线方程.
解:
故,切线方程为:
即:
求曲线在某点处的切线方程的基本步骤:
①求出P点的坐标;
②利用切线斜率的定义求
出切线的斜率;
③利用点斜式求切线方程.
例2 如图, 它表示跳水运动中高度随时间变化的函数
的图象. 根据图象, 请描述、比较
曲线 在 附近的变化情况.
t
o
h
t0
t1
t2
l0
l1
l2
t4
t3
例2
解:可用曲线 h(t) 在 t0 , t1 , t2 处的切线刻画曲线 h(t) 在上述三个时刻附近的变化情况.
(1)当 t = t0 时, 曲线 h(t) 在 t0 处的切线 l0 平行于 x 轴.故在 t = t0 附近曲线比较平坦, 几乎没有升降.
(2)当 t = t1 时, 曲线 h(t) 在 t1 处的切线 l1 的斜率 h’(t1) <0 .故在t = t1 附近曲线下降,即函数 h(t) 在 t = t1 附近单调递减.
t
o
h
l0
t0
t1
l1
t2
l2
t4
t3
(3)当 t = t2 时, 曲线 h(t) 在 t2处的切线 l2 的斜率 h’(t2) <0 .故在 t = t2 附近曲线下降,即函数 h(t) 在t = t2 附近也单调递减.
从图可以看出,直线 l1 的倾斜程度小于直线 l2 的倾斜程度,这说明 h(t) 曲线在 l1 附近比在 l2 附近下降得缓慢
归纳小结
通过观察跳水问题中导数的变化情况,你得到了哪些结论
(1)函数的单调性与其导函数正负的关系 ;
(2)曲线的变化快慢及切线的倾斜程度的内在联系 .
练习:课本80页 B3
从求函数f(x)在x=x0处导数的过程可以看到:当x=x0时, 是一个确定的数。
即:
思考
思考解答
