导数的极值与导数
图片预览







文档简介
(共24张PPT)
3.3.2 函数的极值与导数
知 识 回 顾
1、一般地,设函数y=f(x)在某个区间
内可导,则函数在该区间
如果f′(x)>0,
如果f′(x)<0,
则f(x)为增函数;
则f(x)为减函数.
2、用导数法确定函数的单调性时的步骤是:
(1)
(3)
求出函数的导函数
(2)
求解不等式f′(x)>0,求得其解集,再根据解集写出单调递增区间
求解不等式f′(x)<0,求得其解集,
再根据解集写出单调递减区间
求函数的定义域
跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系
h(t)=-4.9t 2+6.5t+10
其图象如右.
单调递增
单调递减
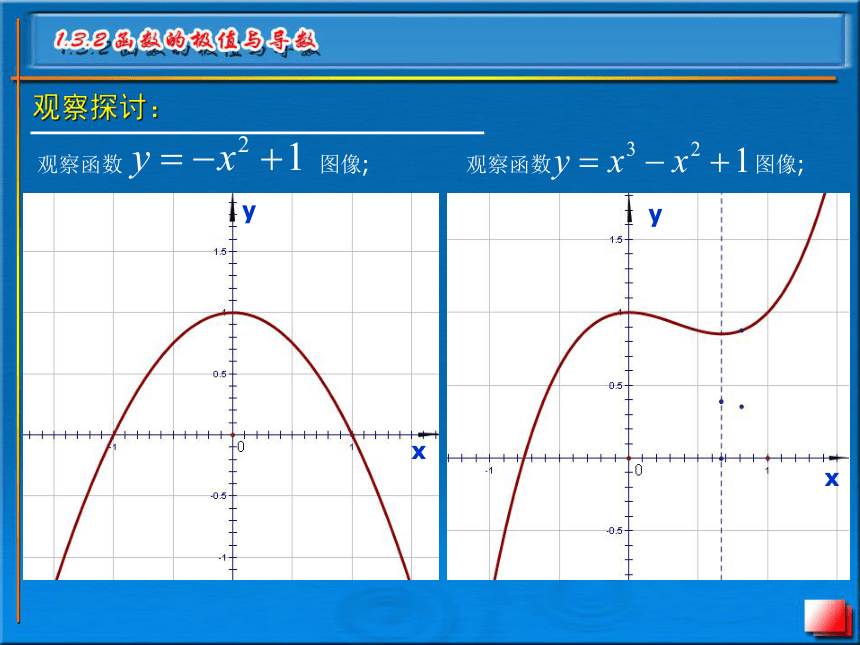
观察探讨:
观察函数 图像;
观察函数 图像;
x
y
y
x
一般地, 设函数 f (x) 在点x0附近有定义, 如果对x0附近的所有的点, 都有
我们就说 f (x0)是 f (x)的一
个极大值, 点x0叫做函数 y = f (x)的极大值点.
反之, 若 , 则称 f (x0) 是 f (x) 的一个极小值, 点x0叫做函数 y = f (x)的极小值点.
极小值点、极大值点统称为极值点, 极大值和极小值统称为极值.
x
y
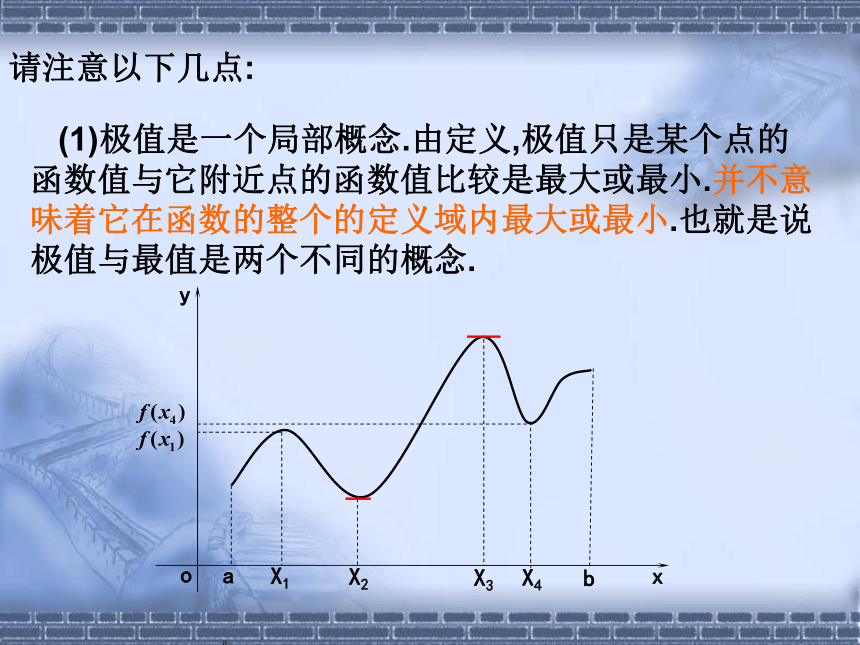
请注意以下几点:
(1)极值是一个局部概念.由定义,极值只是某个点的函数值与它附近点的函数值比较是最大或最小.并不意味着它在函数的整个的定义域内最大或最小.也就是说极值与最值是两个不同的概念.
o
a
X1
X2
X3
X4
b
a
x
y
(2)函数的极值不是唯一的.即一个函数在某区间上或定义域内极大值或极小值可以不止一个.
(3)极大值与极小值之间无确定的大小关系.即一个函数的极大值未必大于极小值,如下图所示,x1是极大值点,x4是极小值点,而f(x4)>f(x1).
o
a
X1
X2
X3
X4
b
a
x
y
(4)函数的极值点一定在区间的内部,区间的端点不能成为极值点。
o
a
X1
X2
X3
X4
b
a
x
y
【问题探究】
函数y=f(x)在极值点的导数值为多少 在极值点附近的导数符号有什么规律
y
a
b
x1
x2
x3
x4
O
x
(1)如果f /(x0)=0, 并且在x0附近的左侧 f /(x)>0
右侧f /(x)<0, 那么f(x0)是极大值
【函数的极值与导数的关系】
(2)如果f /(x0)=0, 并且在x0附近的左侧 f /(x)<0
右侧f /(x)>0, 那么f(x0)是极小值
观察图像并类比于函数的单调性与导数关系的研究方法,看极值与导数之间有什么关系
o
a
x0
b
x
y
x x0左侧 x0 x0右侧
f (x)
f(x)
o
a
x0
b
x
y
x x0左侧 x0 x0右侧
f (x)
f(x)
增
f (x) >0
f (x) =0
f (x) <0
极大值
减
f (x) <0
f (x) =0
增
减
极小值
f (x) >0
求可导函数f(x)极值的 步骤:
(2)求导数f ’(x);
(3)求方程f ’(x)=0的根;
(1) 确定函数的定义域;
f (x)<0
y
x
O
x1
a
b
y=f(x)
在极大值点附近
在极小值点附近
f (x)<0
f (x)>0
f (x)>0
x2
求可导函数f(x)极值的 步骤:
(2)求导数f ’(x);
(3)求方程f ’(x)=0的根;
(4)把定义域划分为部分区间,并列成表格
检查f ’(x)在方程根左右的符号——
如果左正右负(+ ~ -),
那么f(x)在这个根处取得极大值;
如果左负右正(- ~ +),
那么f(x)在这个根处取得极小值;
(1) 确定函数的定义域;
y
x
O
观察与思考:极值与导数有何关系?
在极值点处,曲线如果有切线,则切线是水平的。
a
b
y=f(x)
x1
f (x1)=0
x2
f (x2)=0
x3
f (x3)=0
x4
f (x5)=0
x5
例4、求函数f(x)=x3-12x+12的极值。
解: =3x2-12=3(x-2)(x+2)
令 =0
得x=2,或x=-2
下面分两种情况讨论:
(1)当 >0即x>2,或x<-2时;
(2)当 <0即-2x (-∞,-2) -2 (-2,2) 2 (2,+∞)
+ 0 - 0 +
f(x) 单调递增↗ 28 单调递减↘ -4 单调递增↗
当x变化时, , f(x)的变化情况如下表;
因此,当x=-2时,f(x)有极大值,
并且极大值为f(-2)=28
当x=2时,f(x)有极小值,
并且极小值为f(2)=-4
图象如右
练习:课本96页 1
练习:课本96页 2
3.3.2 函数的极值与导数
知 识 回 顾
1、一般地,设函数y=f(x)在某个区间
内可导,则函数在该区间
如果f′(x)>0,
如果f′(x)<0,
则f(x)为增函数;
则f(x)为减函数.
2、用导数法确定函数的单调性时的步骤是:
(1)
(3)
求出函数的导函数
(2)
求解不等式f′(x)>0,求得其解集,再根据解集写出单调递增区间
求解不等式f′(x)<0,求得其解集,
再根据解集写出单调递减区间
求函数的定义域
跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系
h(t)=-4.9t 2+6.5t+10
其图象如右.
单调递增
单调递减
观察探讨:
观察函数 图像;
观察函数 图像;
x
y
y
x
一般地, 设函数 f (x) 在点x0附近有定义, 如果对x0附近的所有的点, 都有
我们就说 f (x0)是 f (x)的一
个极大值, 点x0叫做函数 y = f (x)的极大值点.
反之, 若 , 则称 f (x0) 是 f (x) 的一个极小值, 点x0叫做函数 y = f (x)的极小值点.
极小值点、极大值点统称为极值点, 极大值和极小值统称为极值.
x
y
请注意以下几点:
(1)极值是一个局部概念.由定义,极值只是某个点的函数值与它附近点的函数值比较是最大或最小.并不意味着它在函数的整个的定义域内最大或最小.也就是说极值与最值是两个不同的概念.
o
a
X1
X2
X3
X4
b
a
x
y
(2)函数的极值不是唯一的.即一个函数在某区间上或定义域内极大值或极小值可以不止一个.
(3)极大值与极小值之间无确定的大小关系.即一个函数的极大值未必大于极小值,如下图所示,x1是极大值点,x4是极小值点,而f(x4)>f(x1).
o
a
X1
X2
X3
X4
b
a
x
y
(4)函数的极值点一定在区间的内部,区间的端点不能成为极值点。
o
a
X1
X2
X3
X4
b
a
x
y
【问题探究】
函数y=f(x)在极值点的导数值为多少 在极值点附近的导数符号有什么规律
y
a
b
x1
x2
x3
x4
O
x
(1)如果f /(x0)=0, 并且在x0附近的左侧 f /(x)>0
右侧f /(x)<0, 那么f(x0)是极大值
【函数的极值与导数的关系】
(2)如果f /(x0)=0, 并且在x0附近的左侧 f /(x)<0
右侧f /(x)>0, 那么f(x0)是极小值
观察图像并类比于函数的单调性与导数关系的研究方法,看极值与导数之间有什么关系
o
a
x0
b
x
y
x x0左侧 x0 x0右侧
f (x)
f(x)
o
a
x0
b
x
y
x x0左侧 x0 x0右侧
f (x)
f(x)
增
f (x) >0
f (x) =0
f (x) <0
极大值
减
f (x) <0
f (x) =0
增
减
极小值
f (x) >0
求可导函数f(x)极值的 步骤:
(2)求导数f ’(x);
(3)求方程f ’(x)=0的根;
(1) 确定函数的定义域;
f (x)<0
y
x
O
x1
a
b
y=f(x)
在极大值点附近
在极小值点附近
f (x)<0
f (x)>0
f (x)>0
x2
求可导函数f(x)极值的 步骤:
(2)求导数f ’(x);
(3)求方程f ’(x)=0的根;
(4)把定义域划分为部分区间,并列成表格
检查f ’(x)在方程根左右的符号——
如果左正右负(+ ~ -),
那么f(x)在这个根处取得极大值;
如果左负右正(- ~ +),
那么f(x)在这个根处取得极小值;
(1) 确定函数的定义域;
y
x
O
观察与思考:极值与导数有何关系?
在极值点处,曲线如果有切线,则切线是水平的。
a
b
y=f(x)
x1
f (x1)=0
x2
f (x2)=0
x3
f (x3)=0
x4
f (x5)=0
x5
例4、求函数f(x)=x3-12x+12的极值。
解: =3x2-12=3(x-2)(x+2)
令 =0
得x=2,或x=-2
下面分两种情况讨论:
(1)当 >0即x>2,或x<-2时;
(2)当 <0即-2
+ 0 - 0 +
f(x) 单调递增↗ 28 单调递减↘ -4 单调递增↗
当x变化时, , f(x)的变化情况如下表;
因此,当x=-2时,f(x)有极大值,
并且极大值为f(-2)=28
当x=2时,f(x)有极小值,
并且极小值为f(2)=-4
图象如右
练习:课本96页 1
练习:课本96页 2
