7[1].2用代入法解二元一次方程组课件
文档属性
| 名称 | 7[1].2用代入法解二元一次方程组课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 533.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-10 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
第七章 用代入法解
二元一次方程组
在 , , , ,
各组值中,
(1)方程y=2x-3的解有——————
(2)方程3x+2y=1的解有——————
(3)方程组 的解有————————
温顾而知新:
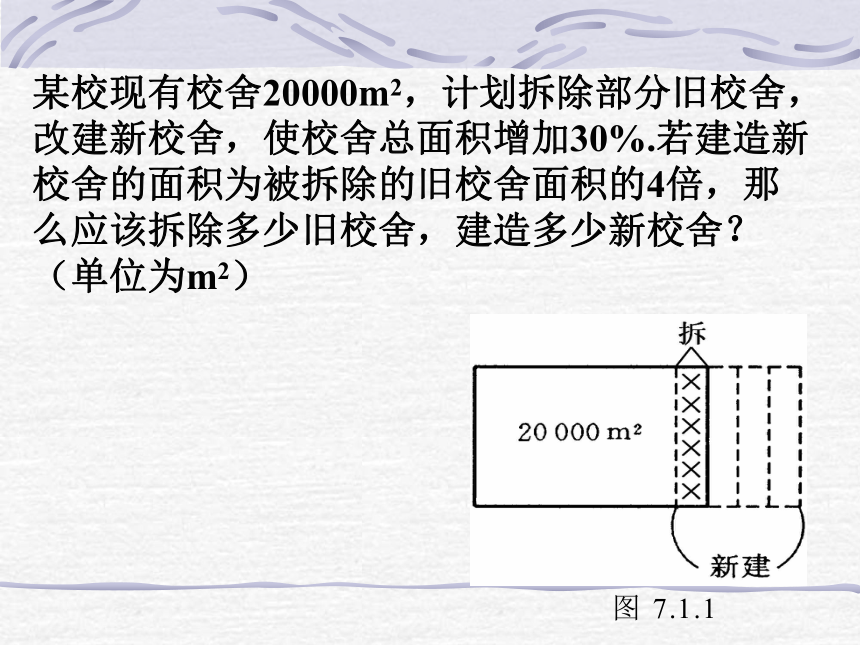
某校现有校舍20000m2,计划拆除部分旧校舍,改建新校舍,使校舍总面积增加30%.若建造新校舍的面积为被拆除的旧校舍面积的4倍,那么应该拆除多少旧校舍,建造多少新校舍?(单位为m2)
如果设应拆除上校舍xm2,建造新校舍ym2,那么根据题意可列出方程组
①
②
怎样求这个二元一次方程组的解呢?
①
②
y
3x=6000
X=2000
把x=2000代入②式,得
y=8000
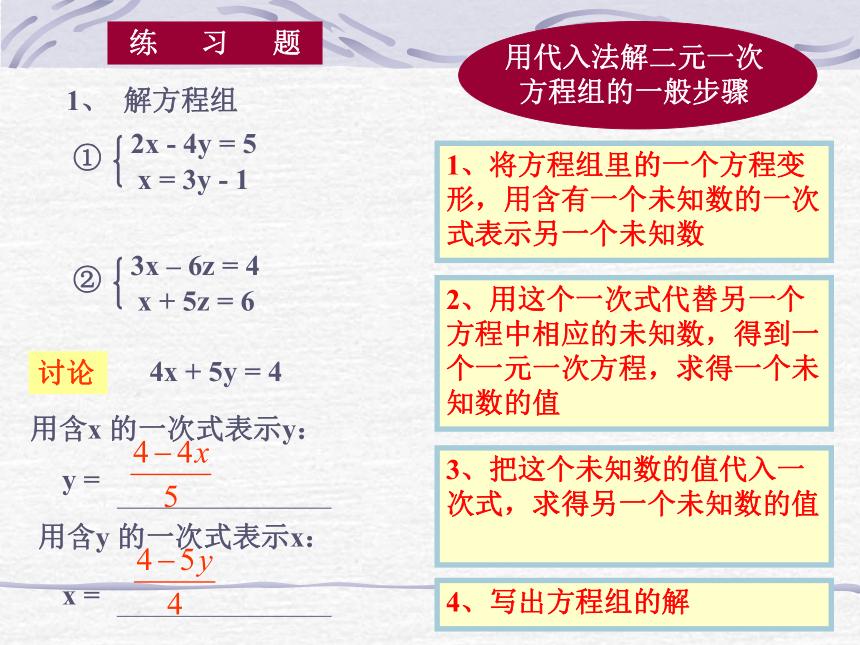
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数
2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值
3、把这个未知数的值代入一次式,求得另一个未知数的值
4、写出方程组的解
用代入法解二元一次方程组的一般步骤
解二元一次方程组
用代入法
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数
2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值
3、把这个未知数的值代入一次式,求得另一个未知数的值
4、写出方程组的解
用代入法解二元一次方程组的一般步骤
练 习 题
1、 解方程组
2x - 4y = 5
x = 3y - 1
①
3x – 6z = 4
x + 5z = 6
②
讨论
4x + 5y = 4
用含x 的一次式表示y:
用含y 的一次式表示x:
x =
y =
例1 解方程组
解
①
②
2s = 3t
3s – 2t = 5
由①得:
s = 3/2 t
③
把③代入②得:
3×3/2 t – 2t = 5
9/2 t – 2t = 5
9t – 4t = 10
5t = 10
t = 2
把t = 2代入③,得
s = 3/2 t
= 3/2×2
= 3
∴
s = 3
t = 2
2s = 3t
3s – 2t = 5
练 习 题
1、 用代入法解下列方程组:
3a – 5b = 6
a + 4b = -15
①
5s = 3t
5t – 3s + 5 = 0
②
2(1 – 2x)= 3(y – x)
2(5x – y)- 4(3x – 2y)= 1
1、 用代入法解下列方程组:
解
原方程组可化为:
x + 3y = 2
-2x + 6y = 1
①
②
由①得
x = 2 – 3y
③
把③代入②得:
-2(2 – 3y)+ 6y = 1
-4 + 6y + 6y = 1
6y + 6y = 1 + 4
12y = 5
y = 5/12
把y = 5/12 代入③,得
x = 2 – 3y
= 2 - 3×5/12
x = 3/4
∴
x = 3/4
y = 5/12
想
想
一
解
原方程组可化为:
2、 用代入法解下列方程组:
3x – 2y = 6
x – y = 2
①
②
由②得:
把③代入①得:
x = 2 + y
③
3(2 + y)- 2y = 6
6 + 3y – 2y = 6
y = 0
把y = 0 代入③,得:
x = 2 + y
= 2 + 0
x = 2
∴
x = 2
y = 0
想
想
一
解方程组:
4(x + y)- 5(x – y)= 2
练 习 题
1
1
1、若方程5x 2m+n+4y 3m-2n = 9是关于x、y的二元一次方程,求m 、n 的值.
解
根据已知条件得:
2m + n = 1
3m – 2n = 1
①
②
由①得:
把③代入②得:
n = 1 –2m
③
3m – 2(1 – 2m)= 1
3m – 2 + 4m = 1
7m = 3
m = 3/7
把m = 3/7 代入③,得:
n = 1 –2m
思 考 题
2、已知 是关于 x、y 的方程组 的解,求 a 、 b 的值.
x =-1
y =2,
2x + ay = 3b
ax - by = 1
2x + ay = 3b
ax - by = 1
解
把 x = -1,y = 2 代入方程组 得:
-2 + 2a = 3b
-a – 2b = 1
①
②
思 考 题
由②得:
a = -2b - 1
③
把③代入①得:
-2 + 2(-2b – 1)= 3b
-2 – 4b – 2 = 3b
-4b – 3b = + 2 + 2
-7b = 4
b = -4/7
把b = -4/7 代入③,得:
a = 1/7
∴
a = 1/7
b = -4/7
a = -2b - 1
= -2×(-4/7)-1
思 考 题
3、若方程组 的解与方程组
的解相同,求a 、b的值.
2x - y = 3
3x + 2y = 8
ax + by = 1
bx + 3y = a
解
2x - y = 3
3x + 2y = 8
①
②
由①得:
y = 2x - 3
③
把③代入②得:
3x + 2(2x – 3)= 8
3x + 4x – 6 = 8
3x + 4x = 8 + 6
7x = 14
x = 2
把x = 2 代入③,得:
y = 2x - 3
= 2×2 - 3
=1
∴
x = 2
y = 1
∵ 方程组 的解与
方程组 的解相同
2x - y = 3
3x + 2y = 8
ax + by = 1
bx + 3y = a
∴把 代入方程组
得:
x = 2
y = 1
ax + by = 1
bx + 3y = a
2a + b = 1
2b + 3 = a
④
⑤
解得:
a = 1
b = -1
思 考 题
4、如果∣y + 3x - 2∣+∣5x + 2y -2∣= 0,求 x 、y 的值.
解:
根据已知条件,得:
y + 3x – 2 = 0
5x + 2y – 2 = 0
①
②
由①得:
y = 2 – 3x
把③代入②得:
③
5x + 2(2 – 3x)- 2 = 0
5x + 4 – 6x – 2 = 0
5x – 6x = 2 - 4
-x = -2
x = 2
把x = 2 代入③,得:
y = 2 – 3x
= 2 - 3×2
= -4
∴
x = 2
y = -4
答:x 的值是2,y 的值是-4.
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数
2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值
3、把这个未知数的值代入一次式,求得另一个未知数的值
4、写出方程组的解
用代入法解二元一次方程组的一般步骤
解二元一次方程组
用代入法
3x + 2y =8
2x +3y =12
{
①
②
求x+y得值。
1、已知:
x + 2y +3m=10
4x +3y +2m=15
{
①
②
2、已知:
求x+y+m的值。
探究一:
第七章 用代入法解
二元一次方程组
在 , , , ,
各组值中,
(1)方程y=2x-3的解有——————
(2)方程3x+2y=1的解有——————
(3)方程组 的解有————————
温顾而知新:
某校现有校舍20000m2,计划拆除部分旧校舍,改建新校舍,使校舍总面积增加30%.若建造新校舍的面积为被拆除的旧校舍面积的4倍,那么应该拆除多少旧校舍,建造多少新校舍?(单位为m2)
如果设应拆除上校舍xm2,建造新校舍ym2,那么根据题意可列出方程组
①
②
怎样求这个二元一次方程组的解呢?
①
②
y
3x=6000
X=2000
把x=2000代入②式,得
y=8000
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数
2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值
3、把这个未知数的值代入一次式,求得另一个未知数的值
4、写出方程组的解
用代入法解二元一次方程组的一般步骤
解二元一次方程组
用代入法
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数
2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值
3、把这个未知数的值代入一次式,求得另一个未知数的值
4、写出方程组的解
用代入法解二元一次方程组的一般步骤
练 习 题
1、 解方程组
2x - 4y = 5
x = 3y - 1
①
3x – 6z = 4
x + 5z = 6
②
讨论
4x + 5y = 4
用含x 的一次式表示y:
用含y 的一次式表示x:
x =
y =
例1 解方程组
解
①
②
2s = 3t
3s – 2t = 5
由①得:
s = 3/2 t
③
把③代入②得:
3×3/2 t – 2t = 5
9/2 t – 2t = 5
9t – 4t = 10
5t = 10
t = 2
把t = 2代入③,得
s = 3/2 t
= 3/2×2
= 3
∴
s = 3
t = 2
2s = 3t
3s – 2t = 5
练 习 题
1、 用代入法解下列方程组:
3a – 5b = 6
a + 4b = -15
①
5s = 3t
5t – 3s + 5 = 0
②
2(1 – 2x)= 3(y – x)
2(5x – y)- 4(3x – 2y)= 1
1、 用代入法解下列方程组:
解
原方程组可化为:
x + 3y = 2
-2x + 6y = 1
①
②
由①得
x = 2 – 3y
③
把③代入②得:
-2(2 – 3y)+ 6y = 1
-4 + 6y + 6y = 1
6y + 6y = 1 + 4
12y = 5
y = 5/12
把y = 5/12 代入③,得
x = 2 – 3y
= 2 - 3×5/12
x = 3/4
∴
x = 3/4
y = 5/12
想
想
一
解
原方程组可化为:
2、 用代入法解下列方程组:
3x – 2y = 6
x – y = 2
①
②
由②得:
把③代入①得:
x = 2 + y
③
3(2 + y)- 2y = 6
6 + 3y – 2y = 6
y = 0
把y = 0 代入③,得:
x = 2 + y
= 2 + 0
x = 2
∴
x = 2
y = 0
想
想
一
解方程组:
4(x + y)- 5(x – y)= 2
练 习 题
1
1
1、若方程5x 2m+n+4y 3m-2n = 9是关于x、y的二元一次方程,求m 、n 的值.
解
根据已知条件得:
2m + n = 1
3m – 2n = 1
①
②
由①得:
把③代入②得:
n = 1 –2m
③
3m – 2(1 – 2m)= 1
3m – 2 + 4m = 1
7m = 3
m = 3/7
把m = 3/7 代入③,得:
n = 1 –2m
思 考 题
2、已知 是关于 x、y 的方程组 的解,求 a 、 b 的值.
x =-1
y =2,
2x + ay = 3b
ax - by = 1
2x + ay = 3b
ax - by = 1
解
把 x = -1,y = 2 代入方程组 得:
-2 + 2a = 3b
-a – 2b = 1
①
②
思 考 题
由②得:
a = -2b - 1
③
把③代入①得:
-2 + 2(-2b – 1)= 3b
-2 – 4b – 2 = 3b
-4b – 3b = + 2 + 2
-7b = 4
b = -4/7
把b = -4/7 代入③,得:
a = 1/7
∴
a = 1/7
b = -4/7
a = -2b - 1
= -2×(-4/7)-1
思 考 题
3、若方程组 的解与方程组
的解相同,求a 、b的值.
2x - y = 3
3x + 2y = 8
ax + by = 1
bx + 3y = a
解
2x - y = 3
3x + 2y = 8
①
②
由①得:
y = 2x - 3
③
把③代入②得:
3x + 2(2x – 3)= 8
3x + 4x – 6 = 8
3x + 4x = 8 + 6
7x = 14
x = 2
把x = 2 代入③,得:
y = 2x - 3
= 2×2 - 3
=1
∴
x = 2
y = 1
∵ 方程组 的解与
方程组 的解相同
2x - y = 3
3x + 2y = 8
ax + by = 1
bx + 3y = a
∴把 代入方程组
得:
x = 2
y = 1
ax + by = 1
bx + 3y = a
2a + b = 1
2b + 3 = a
④
⑤
解得:
a = 1
b = -1
思 考 题
4、如果∣y + 3x - 2∣+∣5x + 2y -2∣= 0,求 x 、y 的值.
解:
根据已知条件,得:
y + 3x – 2 = 0
5x + 2y – 2 = 0
①
②
由①得:
y = 2 – 3x
把③代入②得:
③
5x + 2(2 – 3x)- 2 = 0
5x + 4 – 6x – 2 = 0
5x – 6x = 2 - 4
-x = -2
x = 2
把x = 2 代入③,得:
y = 2 – 3x
= 2 - 3×2
= -4
∴
x = 2
y = -4
答:x 的值是2,y 的值是-4.
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数
2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值
3、把这个未知数的值代入一次式,求得另一个未知数的值
4、写出方程组的解
用代入法解二元一次方程组的一般步骤
解二元一次方程组
用代入法
3x + 2y =8
2x +3y =12
{
①
②
求x+y得值。
1、已知:
x + 2y +3m=10
4x +3y +2m=15
{
①
②
2、已知:
求x+y+m的值。
探究一:
