西师版五年级下册数学总复习全套(121张幻灯片)
文档属性
| 名称 | 西师版五年级下册数学总复习全套(121张幻灯片) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-07 00:00:00 | ||
图片预览







文档简介
西师版 五年级数学期末总复习
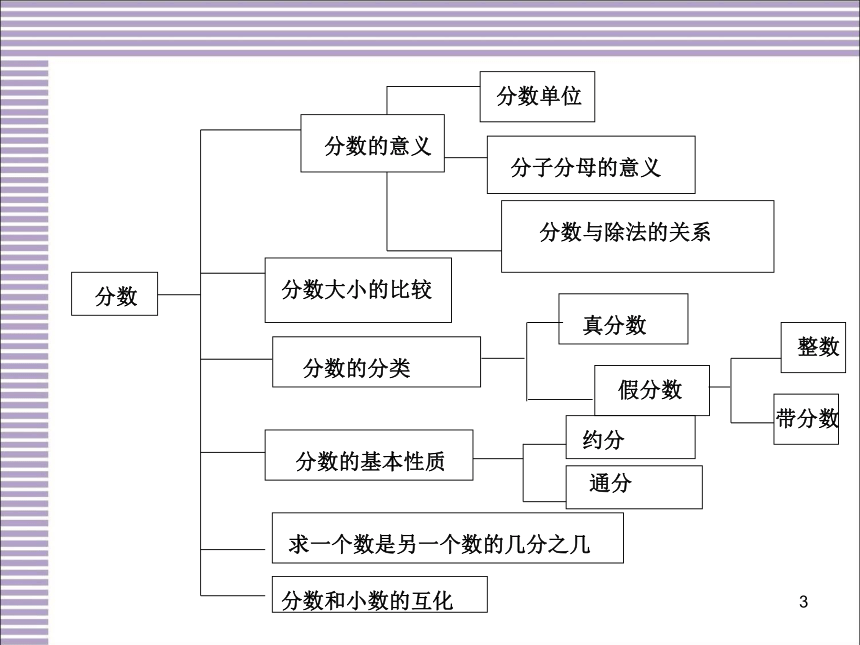
第一单元
分数的意义和性质
分数
分数的意义
分数单位
分子分母的意义
分数与除法的关系
分数大小的比较
分数的分类
真分数
假分数
整数
带分数
分数的基本性质
约分
通分
求一个数是另一个数的几分之几
分数和小数的互化
表示把单位“1”平均分成 5 份,取其中 2 份。还表示把2平均分成5份,取其中1份。
表示 2 个 。
表示 2 除以 5 的商。
(分数的意义)
一个物体、一些物体等都可以看作一个整体,把这个整体平均分成若干份,这样的一份或几份都可以用分数来表示。
分数的意义
单位“1”表示:一个物体、一些物体等都可以看作一个整体,一个整体可以用自然数1来表示,通常把它叫做“1”。
分数单位表示:把单位“1”平均分成若干份,表示其中一份的数叫分数单位。
单位“1”与分数单位的区别
1.表示把单位“1”平均分成5份,取其中3份的分数是( ),它的分数单位是( ),再添上( )个这样的分数单位就是单位“1”。
2. 里面有( )个 。
( )里面有3个 。
3个 是( )。
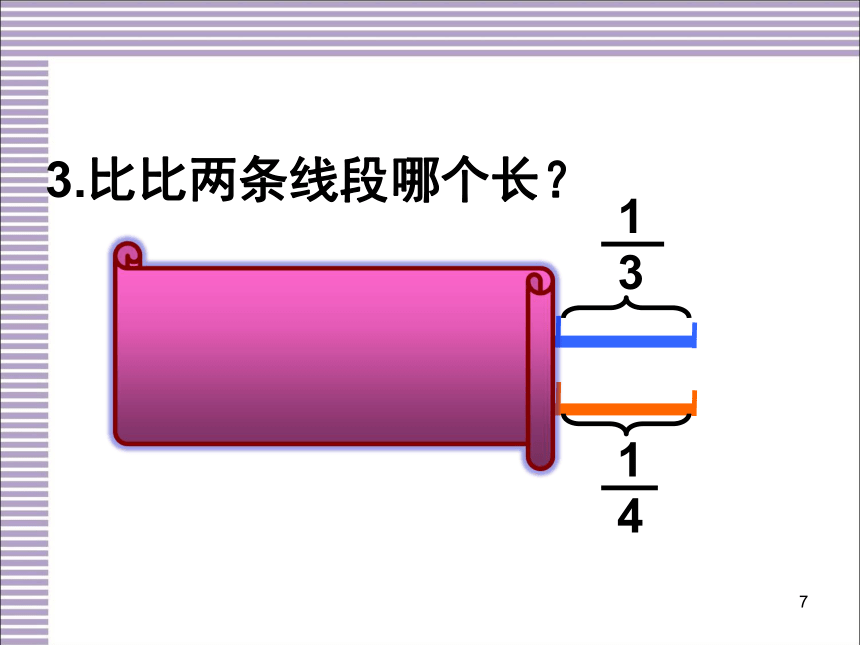
3.比比两条线段哪个长?
1
3
1
4
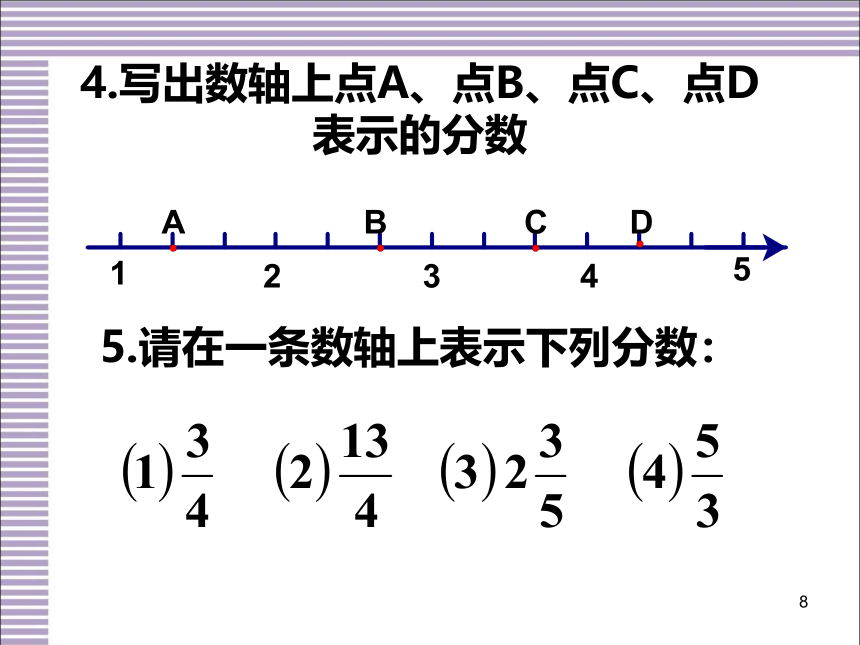
4.写出数轴上点A、点B、点C、点D表示的分数
5.请在一条数轴上表示下列分数:
分数与除法的关系
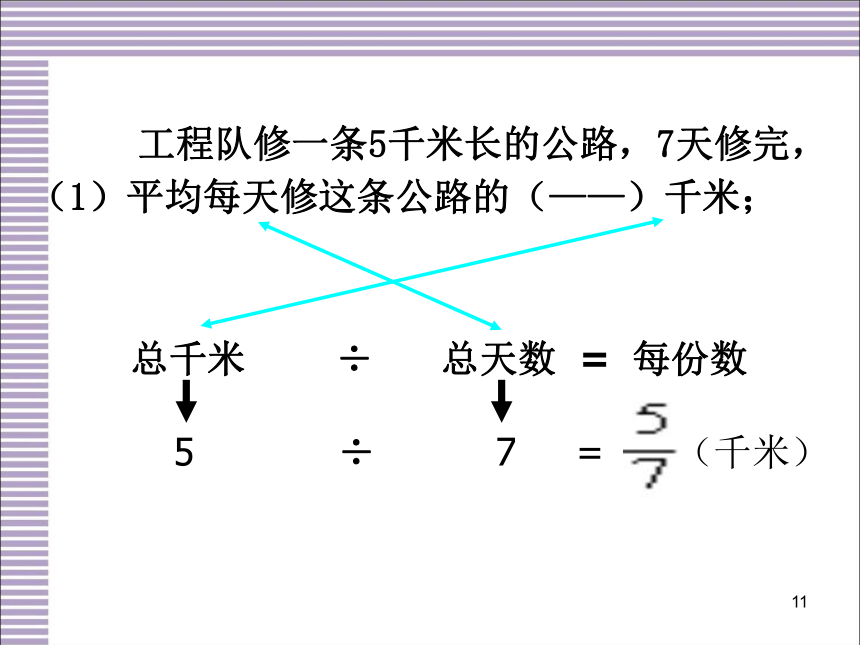
工程队修一条5千米长的公路,7天修完,
(1)平均每天修这条公路的(——)千米;
(2)平均每千米要修(——)天;
(3)平均每天修的占这条公路的(——)。
大家有疑问的,可以询问和交流
可以互相讨论下,但要小声点
工程队修一条5千米长的公路,7天修完,
(1)平均每天修这条公路的(——)千米;
总千米 ÷ 总天数 = 每份数
5 ÷ 7 = (千米)
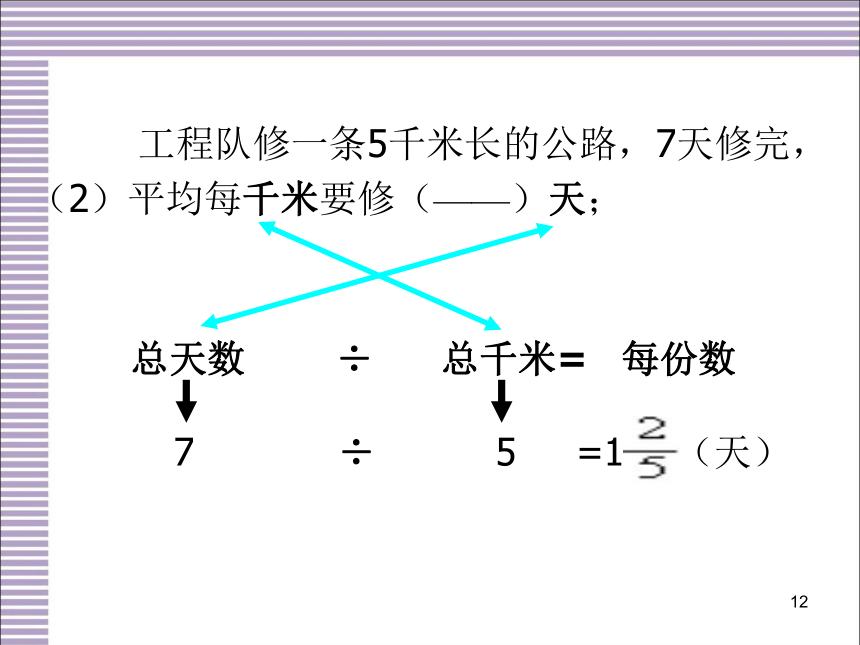
工程队修一条5千米长的公路,7天修完,
(2)平均每千米要修(——)天;
总天数 ÷ 总千米= 每份数
7 ÷ 5 = (天)
1
工程队修一条5千米长的公路,7天修完,
(3)平均每天修的占这条公路的(——)。
1 ÷ 7 =
工程队修一条5千米长的公路,7天修完,
(1)平均每天修这条公路的( )千米;
(2)平均每千米要修( )天;
(3)平均每天修的占这条公路的( )。
1
(4)把4米长的钢筋平均截成5段,
每段长( )米?
总米数 ÷ 总段数 =每份数
4 ÷ 5 = (米)
每段是钢筋全长的(——)
1 ÷ 5 =
(5)一个班有学生50人,其中13人被评为“三好学生”。“三好学生”占全班人数的(——)。
13 ÷ 50 =
小结:分数与除法的关系
分数可以表示整数除法的商,在表示整数除法时,要用除数作分母,用被除数作分子。
用关系式表示:
被除数÷除数= ————
用字母可以表示成:
a÷b= ——
因为除数不能等于“0”,所以b也不能等于“0”。
被除数
除数
a
b
分数与除法是有区别的。除法是一种运算,它有运算符号,是一个算式;而分数是一个“数”,当它在除法算式中的时候,它可以表示除法算式的结果。
小结:当一个量不能用整数个计量单位来表示时,可以用分数来表示。即分数可以表示一个量,分数还可以表示两个量之间的关系。
用分数表示下列除法算式的商。
6÷7=
11÷9=
15÷17=
a÷b=
下图是长方形,它的面积是5平方厘米。请你用阴影表示出
5
8
平方厘米的部分
5平方厘米
5平方厘米
5平方厘米的
1
8
5平方厘米
1平方厘米的
5
8
意义
特征
真分数
分子比分母小的分数
真分数小于1
假分数
分子比分母大或分子和分母相等的分数
假分数都大于或等于1
真分数和假分数
4 的分数单位是( ),去掉( )个
这样的分数单位就是最小的合数。
2
7
的分数单位是( ),再添( )
个这样的分数单位就是最小的质数。
7
8
在 中,a是不为0的自然数。
a
5
(真分数?假分数?最小假分数?最大真分数?)
填空
1.分数的基本性质
分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变。这叫做分数的基本性质。
2.约分
把一个分数化成和它相等,但分子、分母都比较小的分数,叫做约分。
3.通分
把异分母分数分别化成和原来分数相等的同分母分数,叫做通分。
4.最简分数
分子、分母只有公因数1的分数,叫做最简分数。
分数的基本性质
小结:分数的基本性质
约分是分数基本性质中的:分子、分母同时除以相同的数(0除外)的体现。
通分是分数基本性质中的:分子、分母同时乘上相同的数(0除外)的体现。
比较分数的大小除了用同分母、同分子和通分比较方法外,还可以灵活运用其它的方法。
占单位“1”的一半不够
占单位“1”的一半多
﹤
不用通分的方法,比较分数的大小。
因为 ﹥
所以(1— )﹤(1— )
﹤
将分数化为最简分数,可以将分子分母分别除以它们的最大公因数,也可以不断地约分,直到分子分母互质为止。
约分的技巧
分数 的分子加上8,要使分数
大小不变,分母应该( )。
0.6=( ) ÷25=
12
( )
3
5
或3÷5
一个分数的分子扩大20倍,分母缩小20倍,结果如何?
小数化分数,原来有几位小数就在1的后面写几个0做分母,把原来的小数去掉小数点作分子;
化成分数后,能约分的要约分。
分小互化
分小互化
分母是10、100、1000……的分数化小数,可以直接去掉分母,看分母中 1 后面有几个零,就在分子中从最后一位起向左数出几位,点上小数点。
分小互化
分母不是10、100、1000… …的分数化小数,要用分母去除分子;除不尽的,可以根据需要按四舍五入法保留几位小数。
1
2
1
4
2
5
3
4
1
5
1
8
4
5
3
5
3
8
5
8
7
8
1
20
1
16
3
16
5
16
7
16
1
25
1
50
1
40
把下面的分数化成小数,
并且记住这些结果。
3 2 3 1
20
9
5
8
3
3.025
0.16
0.15 0.2222…… 0.6 3.125
0.375
3
20
0.16
3.025
2
9
3
5
3
1
8
?
?
? ? ? ?
0.375
把下面各数按从小到大的顺序排列起来。
在( )里填上合适的分数
50厘米=( )米 250克=( )吨
45分= ( )时 400米=( )千米
600毫米=(— )米 40厘米= (— )米
15秒=( —)分 2500平方米=(— )公顷
50
100
1
2
1
4
3
4
2
5
1 1
4 4
3 2
5 5
互质数特殊的判断方法
① 1和任意自然数互质。
②2和任意奇数都是互质数。
③相邻两个自然数都是互质数。
④相邻的两个奇数都是互质数。
⑤不相同的两个质数是互质数。
⑥当一个数是合数,而另一个数是质数时,若合数不是质数的倍数,一般情况下这两个数也是互质数。
特殊情况
熟练掌握两种特殊情况。
两数关系
最大公因数
最小公倍数
互质关系
1
两数积
倍数关系
较小数
较大数
同时熟记7、11、13、17、19等数的倍数
及11—20所有数的平方数以提高计算速度。
求三个数的最小公倍数的特殊规律:
当三个数两两互质时,最小公倍数是这三个数的积; [2 ,7,9]= 126
当三个数都成整倍数关系时,最大的数就是最小公倍数; [18 ,6,54]= 54
当三个数中有两个数成倍数关系时,那么求三个数的最小公倍数就可转化为求这两个数中较大者与第三个数的最小公倍数等。
[18 ,6,27] [18 ,27]=108
第二单元 长方体和正方体
复习长方体和正方体
第一课时
长方形
正方形
三角形
按边分
按角分
等边三角形
等腰三角形
一般三角形
锐角三角形
直角角三角形
钝角三角形
平行四边形
梯形
等腰梯形
直角梯形
一般梯形
组合图形
平面图形
一、建构知识网络
立体图形
正方体
长方体
二、 注重知识的承接,回顾所学平面图形的特征、周长和面积公式。
名称
特征
周长(c)
面积(s)
长方形
两组对边分别平行且相等
(长+宽)×2
C=2(a+b)
长×宽
S=ab
正方形
四边相等
边长×4
C=4a
边长×边长
S=a?
平行四边形
两组对边平行且相等
底×高
S=ah
梯形
只有一组对边平行
(上底+下底)×高÷2
三角形
三条边,三个内角的和等于180°
(底×高)÷2
ah
S=
1
2
(a+b)h
S=
1
2
三、 明确长方体、正方体的异同。
从点、棱、面三方面比较长方体和正方体之间的相同点和不同点
长方体
正方体
相同点
6个面、12条棱、8个顶点
不同点
6个面都是长方形(有时相对的两个面是正方形),相对面完全相同。
6个面都是正方形,
6个面完全相同
相对棱的长度相等
12条棱长度都相等
正方体是特殊的长方体。
用集合图表示:
长方体
正方体
四、 复习长方体、正方体表面积的含义
15
10
8
后
前
上
下
左
右
●
15
10
8
单位:厘米
长方体六个面的面积,就是长方体的表面积。
1.长方体表面积的含义
2.正方体表面积的含义
(1)正方体棱长与每个面边长的关系
后
上
前
下
左
右
正方体展开图的每个面都是正方形,边长就是正方体的棱长,每个面的面积都等于棱长乘棱长。
(2)正方体的11种展开图。
图(1)
图(2)
图(3)
图(4)
图(5)
图(6)
第一类:中间四连方,两侧各有一个,共6种
第二类:中间三连方,一侧有一个、一侧有二个,共3种
图(7)
图(8)
图(9)
第三类:中间两连方,两侧各有2个,只有1种
图(10)
第四类:两排各有3个,只有1种
图(11)
五、复习长方体、正方体体积公式的推导
长方体的体积 = 长 × 宽 × 高
底面积
正方体的体积 = 棱长 ×棱长×棱长
底面积
可看作是高
长方体(或正方体)的
体积 = 底面积 × 高
六、体积与容积区别与联系
异同点
体积
容积
区别
意义不同
物体所占空间的大小,叫做物体的体积。
一个容器所能容纳物体的体积,叫做这个容器的容积。
测量方法不同
从物体外部测量长、宽、高。
从容器里面测量长、宽、高。
单位名称不同
m?、dm?、cm?。
容积单位:L和ml;计量固体时用体积单位。
联系
容积的大小是通过所能容纳物体的体积表示出来的。
计算方法相同
7厘米
5厘米
5厘米
这个长方体的长是( 7 )厘米,宽是( 5 )厘米,高是( 5 )厘米,这个长方体有( 2 )个面是正方形,有( 4 )个面是长方形。
如图
1.
2. 要焊接一个长10cm,宽8cm,高6cm的长方体框架,要准备10cm,宽8cm,高6cm的铁丝各( 4 )根。
3.一个正方体纸盒的棱长是7cm,这个纸盒的棱长总和是(84 )cm。
4.有一根150cm长的铁丝,用这根铁丝焊成了一个正方体的框架,还剩铁丝6cm。这个正方体框架的棱长是( )厘米。
七、基础知识的练习
150cm
12
8.有一个长方体,底面是一个正方形,高18cm,侧面展开正好是一个正方形。这个长方体的体积是( 364.5 ) cm? 。
18÷4=4.5(cm)
4.5×4.5×18
=20.25×18
=364.5(cm?)
18cm
18cm
18cm
10.把棱长是1厘米的小正方体拼摆在一起。如果从右面看,所看到的图形面积是( 7 )平方厘米,体积是( 11 )立方厘米。
11.
一个棱长为2cm的正方体,在它的一个角上挖掉一个棱长为1cm的小正方体,它的表面积是 (??? 24 )cm?。
第二课时:解决相关的实际问题
12cm
15cm
8cm
1. 一条彩带捆扎一种礼盒(如图),如果
接头处的彩带长30cm,求这条彩带的长度。
8×4+12×2+15×2+30=116(cm)
答:这条彩带长116厘米。
2.与右面正方体一致的展开图是( )。
B
1
2
3
1
2
3
2
3
1
1
2
3
C
B
A
甲
乙
取出石块后
2.1dm
1.8dm
3. 图中有两个完全一样的长方体水箱,水箱的底面积是2平方分米,请结合图中所给信息求出甲箱中石块的体积是多少?
2×(2.1-1.8)=0.6(dm?)
答:石块的体积是0.6dm?。
前
右
6
3
7
4.小明从一个长方体纸盒上撕下两个相邻的面(展开后如图,单位:厘米),这个纸盒的底面积是( )平方厘米,体积是( )立方厘米。
底面积:6×3=18(平方厘米)
18
126
体积:6×3×7=126(立方厘米)
5厘米
5厘米
5厘米
5.把 积木装入纸箱内,纸箱从里面量,长25厘米,宽和高都是20厘米。纸箱最多可容纳积木多少块?
(25÷5)×(20÷5)×(20÷5)
=5×4×4
=80(块)
答:纸箱最多可容纳积木80块。
6.把 积木装入纸箱内,纸箱从里面量,长25厘米,宽和高都是20厘米。纸箱最多可容纳积木多少块?
5厘米
3厘米
3厘米
(25÷3)×(20÷3)×(20÷5)
≈8×6×4
=192(块)
答:纸箱最多可容纳积木192块。
7.一块长方形铁皮,长40cm,宽30cm,像下图这样从4个角各剪掉一个边长为5厘米的正方形,然后做成盒子,这个盒子的容积是多少升?
40cm
30cm
(40-5×2)×(30-5×2)×5=3000(cm?)
3000cm?=3L
答:这个盒子的容积是3升。
12ml=12cm3 24ml=24cm3
一个小球的体积:(24-12) ÷(4-1)=4(cm3)
一个大球的体积:12-4=8(cm3)
左图长、宽、高分别是4cm、3cm、3cm。
它的体积是:
4×3×3=36(cm2)
右图长、宽、高分别是4cm、3cm、4cm。
它的体积是:
4×3×4=48(cm2)
10.用3个长5cm,宽4cm,高3cm的长方体木块,拼成一个表面积最小的长方体。这个长方体的表面积是多少平方厘米?
5cm
4cm
3cm
[5×4+5×(3×3)+4×(3×3)]×2=(20+45+36)×2=202(cm?)
答:这个长方体的表面积是202平方厘米。
3cm
2cm
6cm
6cm
11.有一个形状如图的零件,由一个长方体和一个
正方体组合而成。长方体的长和宽都是6cm,高是3cm,正方体的棱长是2cm。求这个零件的表面积。
2×2×4+6×3×4+6×6×2
=16+72+72
=160(cm?)
答:这个零件的表面积是160平方厘米。
12.由27个棱长为1cm的小正方体组成一个棱长为3cm的大正方体,若自上而下去掉中间的3个小正方体(如图所示),则剩下的几何体的表面积是多少平方厘米?
3×3×6-1×1×2+3×1×4
=54-2+12
=64(cm?)
答:剩下的几何体的表面积是64平方厘米。
13.从一个大长方体上切下一个体积是128立方厘米的小长方体(如图)。原来大长方体的体积是多少立方厘米?
22cm
8cm
切下部分
128÷8×22
=16×22
=352(立方厘米)
答:原来大长方体的体积是352立方厘米。
14. 一个密封的长方体容器里面装有一些水,水深9厘米,如果把这个容器的右面做底,这时容器内的水深多少厘米?
36
10
12
36
10
12
36×10×9=3240(cm3)
3240÷(12×10)=27(cm)
答:容器内的水深27厘米。
第三单元
分数的加法和减法
分数的加法和减法
分数加减法的简算
异分母分数加减法
同分母分数连减
同分母分数连加
同分母分数加减法
分数加减混合运算
异分母分数连加
异分母分数连减
同分母分数相加、减,分母不变,只把分子相加减。
1.同分母分数加减法
(1)同分母分数加法的意义及计算方法
(2)同分母分数减法的意义及计算方法
(3)同分母分数连加、连减
异分母分数加减法,先通分,转化为同分母分数进行计算。
2.异分母分数加减法
(1)异分母分数加法
(2)异分母分数减法
(3)分数加减法混合运算
a.不带括号的分数加减法混合运算
b.带括号的分数加减法混合运算
加法的运算定律和减法的性质同样适应于分数中的计算。
2
7
+
3
7
3
8
+
1
8
5
12
-
3
12
4
9
-
2
9
25
36
-
17
36
-
5
36
9
11
-
1.口算
-
7
11
2
11
注意化简和简算
异分母分数加减法,先通分,转化为同分母分数进行计算。
2.计算
加法的运算定律和减法的性质同样适应于分数中的计算。
1
2
+
1
3
1
3
+
1
7
1
5
-
1
8
1
9
-
1
16
先计算下面各题,想一想怎样计算比较快?
用字母表示为:
1
a
±
1
b
=
b±a
ab
a、b均不为0
1
2
1
4
1
8
1
16
1
32
+
+
+
+
1
32
1
4
1
8
1
16
1
2
1
2
1
4
1
8
1
16
1
32
+
+
+
+
拆项法:
1
2
=
1
-
+
1
2
-
1
4
+
1
4
-
1
8
+
1
8
-
+
1
16
-
1
32
1
16
=
=
1
1
32
-
31
32
学校图书馆有故事书占图书总数的 ,
工具书占总数的 ,
剩下的是科技书,科技书占总数的 几分之几?
1- -
=
-
-
=
答:科技书占总数的 。
在圆圈内填上适当的分数,使每行、每列的三个数加起来的和都等于1。
八.比例问题
1.甲乙两人在河边钓鱼,甲钓了三条,乙钓了两条,正准备吃,有一个人请求跟他们一起吃,于是三人将五条鱼平分了,为了表示感谢,过路人留下10元,甲、乙怎么分?
解:“三人将五条鱼平分,客人拿出10元”,可以理解为五条鱼总价值为30元,那么每条鱼价值6元。又因为“甲钓了三条”,相当于甲吃之前已经出资3*6=18元,“乙钓了两条”,相当于乙吃之前已经出资2*6=12元。而甲乙两人吃了的价值都是10元,所以甲还可以收回18-10=8元乙还可以收回12-10=2元刚好就是客人出的钱。
认真思考
2.一种商品,今年的成本比去年增加了10分之1,但仍保持原售价,因此,每份利润下降了5分之2,那么,今年这种商品的成本占售价的几分之几?
最好画线段图思考:把去年原来成本看成20份,利润看成5份,则今年的成本提高1/10,就是22份,利润下降了2/5,今年的利润只有3份。增加的成本2份刚好是下降利润的2份。售价都是25份。所以,今年的成本占售价的22/25。
简易方程
整理与复习
简易方程
用字母表示确定的数
和不确定的数
用字母表示运算定律
用字母表示计算公式
用字母表示数量关系
方程的意义
解方程
稍复杂的方程
用字母表示数
解简易方程
列方程解决问题
基本的方程
方程
方程的解
解方程
一、用字母表示数
用含有字母的式子表示数、数量关系、公式和定律等。
路程(s)、速度(v)、时间(t)的数量关系:
s=vt v=s÷t t=s÷v
总价(c)、数量(x)、单价(a)的数量关系:
c=ax a=c÷x x=c÷a
运算定律:
a+b=b+a (a+b)+c=a+(b+c)
ab=bc (ab)c=a(bc) (a+b) c=ac+bc
工作总量(c)、工作时间(t)、工作效率(a)的数量关系:
c=at a=c÷t t=c÷a
计算公式:
S =ab C =(a+b)X2
S =a﹒a C =4a
S =ah S =ah÷2
S =(a+b)h÷2
复习:小轿车的速度是a千米/小时,它从广州开往惠州,行了1.5小时后距离惠州还有32千米。
(1)1.5a表示( ? );广州距离惠州有( )千米。
(2)当a=90时,计算广州到惠州的路程。
时间
速度
X
=路程
1.5小时行的路程
总距离
1.5小时行的路程
32千米
1.5a+32
广州
惠州
1.5a+32
= 1.5X90+32
=135+32
167(千米)
一、用字母表示数
1.一个平行四边形的底是a厘米,高3厘米,它的面积是( )平方厘米。
巩固练习---在括号里填上含有字母的式子。
S =ah
=3a
3.小英重n千克,比小华轻3千克,小华体重是( )千克。
C =(a+b )X2
=(48+b)X2
=96+2b
2.一个长方形的长是48分米,宽是b分米,它的周长是( )分米。
一、用字母表示数
小华
比小英重3千克
3a
96+2b
3+n
6.一头奶牛一天可以产奶y千克,6头奶牛一周可以产奶( )千克。
5.学校美术组有X人,体育组的人数是美术组人数的4倍,体育组有( )人。当X=15时,体育组有( )人。
巩固练习---在括号里填上含有字母的式子。
4.汽车平均每小时行m千米,6小时能行( )千米,行450千米要( )小时。
S=vt
=6m
4x=4×15=60
6m
4x
t=S÷v
=450÷m
450÷m
60
工作总量=工作效率 ×工作时间(C=at )
一头奶牛一周的产奶总量= y×7
6头奶牛一周的产奶总量= y×7×6=42y
42y
一、用字母表示数
①当字母与数字相乘时,去掉乘号,把数字写在字母的前面,也可以用点表示乘号,如:a×3通常可以写成3a或3·a。
②当字母与字母相乘时,省略乘号,用点表示或直接去掉乘号,如:a×b写成a·b或ab;(通常按字母的先后顺序写)
③字母与1相乘省略1不写,只写字母本身,如:1×a写成a。
④两个一样的字母相乘就写一个字母,再在字母的右上角写上2,如:a×a通常写成a·a或a2,读作:a的平方。
1.含字母的乘法算式的简写的规则
一、用字母表示数
2.练习
A.填空。
(1)图书角原来有X本书,被同学借走10本后还有( )本。
(2)小芳今年Y岁,妈妈年龄是小芳的6倍,妈妈今年( )岁。
(3)一个正方形的边长是A分米,它的面积是( )平方分米。
(4)公交车上原有w人,到站后下车8人,上车k人,现在车上有( )人。
(5)小明的妈妈今年37岁,比小明大A岁,小明今年( )岁,过30年后妈妈比小明大( )岁。
(6)用a表示长方形的长,用b表示它的宽。
它的面积公式为: 。
它的周长公式为: 。
S=ab
C=(a+b)×2
C=2(a+b)
X-10
6Y
A?
W-8+K
A
37-A
(7)乘法结合律、乘法分配律分别用字母表示
abc=a(bc)
a(b+c)=ab+ac
B.做一做:书本p120第3题。
请你用字母表示下面的数量关系。
王叔叔每小时加工a个零件,t小时共加工c个零件。
(1)如果每小时加工30个零件,5小时可以加工( )零件。
(2)如果每小时加工25个零件,( )小时可以加工100个零件。
C=at
a=C÷t
t=C÷a
150
4
(1)等式的意义:表示等号两边是相等关系的式子叫等式。
二、方程的概念
如:3+6.5=9.5、 3.6× 0.5=1.8、 3.5+x=9.5等都是等式。
(2)方程的意义:
如: x + 3.2=8、 11x=363、x÷7.6=11.4等都是方程。
3x+1>5 、 x-12.5﹤5 3+6.5=9.5等不是方程。
(3)方程与等式的关系:
如:35 ÷7=5、2x=0、 3.5x=4、11.2-x=11.14等都是等式,
但 35÷ 7=5 不是方程。
含有未知数的等式叫方程。
等式的范围比方程的范围大。
方程都是等式,但等式不一定是方程。
等式的性质:
等式两边同时加上(减去)一个数,左右两边仍然相等;
等式两边同时乘或除以一个(不为0)的数,左右两边仍然相等。
二、方程的概念
巩固练习----判断。
1、等式不一定是方程,方程一定是等式。 ( )
2、因为100-25x,含有未知数x,所以它是方程。 ( )
3、含有未知数的算式叫做方程?.?? ????????? (? ?)
???????????????????
(3x+1>5不是方程)
(100-25x=0 ?)?
(等式的范围比方程的范围大。)
√
×
×
方程的意义
1、什么叫方程?
2、方程的条件有哪些?
3、什么叫方程的解?
4、什么叫解方程?
方程的解实际上是 .
一个数
一个过程
解方程实际上是 .
未知数、等式
含有未知数的等式.
使方程左右两边相等的未知数的值,叫做方程的解
求方程的解的过程叫做解方程
2.练一练:将序号填入圈中。
⑴ 30+2=32 ⑵ 3×X ⑶ X-T=6
⑷ 4+A>18 ⑸ 25÷v=Z ⑹ 5.6-4=G
方程
等式
不是等式
⑵
⑶
⑷
⑸
⑹
⑴
⑶
⑸
⑹
方程与等式之间的关系
等 式
方程一定是等式;
但等式不一定是方程。
方程
简易方程
整理与复习
解方程的原理是什么?要注意什么?
(1)等式的两边同时加上或减去相同的数,等式不变。
(2)等式的两边同时乘或除以相同的数(0除外),等式不变。
同加同减
同乘同除
3.解方程(打★写出检验过程)
5(X-1.5)=17.5
4X-1.2X=4.2
解:
★
5(X-1.5)÷5=17.5÷5
X-1.5=3.5
X-1.5+1.5=3.5+1.5
X=5
检验:方程左边=
5(X-1.5)
=5×(5-1.5)
=17.5
=5×3.5
=方程右边
所以,X=5是方程的解。
解:
(4-1.2)X=4.2
2.8X=4.2
2.8X÷2.8=4.2÷2.8
X=1.5
χ-12=30
у+12=42
6χ=30
χ÷5=30
解:χ-12+12=30+12
解:у+12-12=42-12
解:6χ÷6=30÷6
解:χ÷5×5=30×5
χ=42
у=30
χ=5
χ=150
χ-12=30
у+12=42
6χ=30
χ÷5=30
6χ+12=42
解:6χ+12-12=42-12
6χ=30
6χ÷6=30÷6
χ=5
6χ+2×6=42
解:6χ+12=42
6χ+12-12=42-12
6χ=30
6χ÷6=30÷6
χ=5
6(χ+2)=42
解:6(χ+2)÷6=42÷6
χ+2=7
χ+2-2=7-2
χ=5
5χ+χ=30
解:6χ=30
6χ÷6=30÷6
χ=5
6χ+12=42
解:6χ+1 2-12=42-12
6χ=30
6χ÷6=30÷6
χ=5
6χ+2×6=42
解:6χ+12=42
6χ+12-12=42-12
6χ=30
6χ÷6=30÷6
χ=5
6(χ+2)=42
解:6(χ+2)÷6=42÷6
χ+2=7
χ+2-2=7-2
χ=5
5χ+χ=30
解:6χ=30
6χ÷6=30÷6
χ=5
解:6χ=42-12
χ=30÷6
6χ=42-12
χ=30÷6
χ=30÷6
解:χ+2=42÷6
χ=7-2
刚才这些方程可不可以简化解方程的过程?
三.解方程
x+5=12.3 x-6=9.2 4x=24.8 x÷2=16.2
解方程的依据---等式的性质。
方程两边同时加上(减去)一个数,左右两边仍然相等;
方程两边同时乘或除以一个(不为0)的数,左右两边仍然相等。
1.简单方程:
-5
-5
+6
+6
÷4
÷4
×2
×2
解:
x=12.3- 5
x=7.3
解:
x=9.2 +6
x=15.2
解:
x=24.8 ÷4
x=6.2
解:
x=16.2 ×2
x=32.4
三.解方程
(1)1.2x-4.4=5.6×2
解复杂方程的要点:
1、能计算的要先算.
2、把和X在一起或较近的数看作一个整体.
2.复杂方程:
把1.2X看作是一个整体,先算5.6×2 .
+4.4
+4.4
解:
1.2x-4.4= 11.2
1.2x=11.2+4.4
1.2x=15.6
x=15.6÷1.2
÷1.2
÷1.2
x=13
三.解方程
(2) 2.7X+0.9X=1.44
2.复杂方程:
先算2.7X+0.9X.
解:
3.6x= 1.44
x = 1.44÷3.6
÷3.6
÷3.6
x = 0.4
解复杂方程的要点:
1、能计算的要先算.
2、把和X在一起或较近的数看作一个整体.
三.解方程
(3)0.6(x÷8)=0.9
2.复杂方程:
把x÷8 看作是一个整体.
解:
x÷8 = 0.9÷0.6
x÷8 = 1.5
÷0.6
÷0.6
x = 1.5×8
×8
×8
x = 12
验算:方程左边=0.6×(12÷8) =0.9=右边
所以, X = 12是原方程的解。
解简易方程
X+7.8=20.2 x-6=12.5
5X=20.5 x÷6=18.6
5.6 X-8.6=19.4
2 X+1.2×5=7
3.2 X-1.5 X=0.51
(4.5+X)×2=13
简易方程
整理与复习
说说列方程解应用题的步骤:
1、读题(至少读3遍),弄清题目中的数量关系。
2、写出等量关系式。能用线段图最好
3、找出等量关系式中的未知数,设为X。
4、根据等量关系式列出方程。
5、解方程。
6、检验。
列方程解应用题
A.说出下面各题中数量之间的相等关系。
(1)养禽场一共养鸡鸭600只。
(2)红花比黄花少25朵。
(3)参加航模组的人数是参加美术组的3倍。
(4)花金鱼比黑金鱼的1.2倍还多8条。
2.练习:
鸡的只数+鸭的只数=一共养的只数
黄花的数量-25朵=红花的数量
一共养的只数-鸡的只数=鸭的只数
黄花的数量-红花的数量=25朵
红花的数量+25朵=黄花的数量
一共养的只数-鸭的只数=鸡的只数
参加美术组的人数×3=参加航母组的人数
参加航母组的人数÷参加美术组的人数=3
参加航母组的人数÷3=参加美术组的人数
黑金鱼的条数×1.2+8=花金鱼的条数
B. 列方程解决问题。
(1)桔树有150棵,比梨树多30棵,梨树有几棵?
(2)桔树有150棵,是梨树的3倍,梨树有几棵?
(3)桔树有150棵,比梨树的3倍还多30棵,梨树有几棵?
(5)桔树和梨树共有150棵,桔树棵数是梨树的2倍, 桔树和梨树各有几棵?
(4)果园运来25捆桔树和梨树,共150棵,已知每捆桔树4棵,每捆梨树有几棵?
解:设梨树有X棵。
梨树棵数+30棵=桔树棵数
x+30=150
解:设梨树有X棵。
梨树棵数×3=桔树棵数
3X=150
解:设梨树有X棵。
梨树棵数×3+30=桔树棵数
3X+30=150
解:设梨树有X棵。
桔树棵数+梨树棵数=150棵
25×4+25X=150
解:设梨树有X棵,那么桔树有2X棵。
2X+X=150
桔树棵数+梨树棵数=150
有两个书架,第一个书架书的本数是第二个的1.5倍。如果从第一个书架取出50本放入第二个中,则两个书架的数就一样多。原来两个书架各有几本书?
解:设第二个书架有x本书,那么第一个书架有1.5x本书。
两个书架相差了(50×2)本
1.5x-x= 50×2
0.5x= 100
第一个书架书的本数-第二个书架书的本数=相差的本数
0.5x÷0.5= 100÷0.5
x= 200
第一个书架:1.5x=1.5×200=300
不写单位
2.有两个书架,第一个书架书的本数是第二个的1.5倍。如果从第一个书架取出50本放入第二个中,则两个书架的数就一样多。原来两个书架各有几本书?
解:设第二个书架有x本书,那么第一个书架有1.5x本书。
1.5x-50= x+50
第一个书架书的本数-50=第二个书架书的本数+50
0.5x-50= 50
第一个书架:1.5x=1.5×200=300
不写单位
1.5x-50-X= x+50-X
0.5x-50+50= 50+50
0.5x= 100
0.5x÷0.5=100÷0.5
x=200
复习一:少年宫合唱队有84人,合唱队的人数比舞蹈队的3倍多15人。舞蹈队有多少人?
舞蹈队人数:
合唱队人数:
X
3X
15
84
想:根据题意,舞蹈队人数的3倍加上15,正好等于合唱队的人数。
解:设舞蹈队有x人。
3X+15=84
3X+15-15=84-15
3X÷3=69÷3
X=23
答:舞蹈队有23人。
复习二:兴华服装厂五月份做大人服装1500套,做的儿童服装比大人服装的3倍少270套。做儿童服装多少套?
大人服装:
儿童服装:
1500
3
270
X
想:根据题意,儿童服装的套数加上270套再除以3正好是大人服装的套数。
解:设做儿童服装X套。
(x+270) ÷3=1500
(X+270) ÷3×3=1500×3
x+270=4500
X+270-270=4500-270
X=4230
答:做儿童服装4230套。
复习三:果园里一共种了340棵桃树和杏树,其中桃树的棵数比杏数的3倍多20棵。两种树各种了多少棵?
杏树的棵数:
桃树的棵数:
X
X
X
X
多20
3X+20
想:这道题要求两个未知数。我们可以先设其中一个未知数为X,根据题意列方程解答,然后再求出另一个未知数。
解:设杏树有X棵。那么桃树有3X+20棵
340
X+3X+20=340
4X+20-20=340-20
4X=320
4X÷4=320÷4
X=80
3X+20=3×80+20
=260
答:杏树有80棵,桃树有260棵。
复习四:有两袋大米,甲袋大米的重量是乙袋的1.2倍。如果再往乙袋里装5千克大米,两袋就一样重了。原来两袋大米各有多少千克?
甲袋:
乙袋:
想:设乙袋有X千克,则甲袋就有1.2X千克,甲袋大米的重量减去乙袋大米的重量刚好等于再往乙袋装的5千克大米。
解: 设乙袋有X千克大米,那么,甲袋有1.2X千克大米。
X
1.2X
5
1.2X-X=5
0.2X=5
0.2X÷0.2=5÷0.2
X=10
1.2X=1.2×10=12
答:原来甲袋大米有12千克,乙袋大米有10千克。
2、妈妈有200元钱,是小红的4倍多20元,小红有多少元?
3、爸爸的年龄比儿子大32岁,是儿子年龄的9倍,爸爸和儿子各多少岁?
4、学校买10套课桌用500元,已知桌子的单价是凳子的4倍,每张桌子多少元?
1、苹果树和梨树共有270棵,苹果树棵数是梨树的2倍, 桔树和梨树各有几棵?
统计与概率
表三:单式折线统计图
表三 光明小学一----六年级喜欢看科普读物人数统计表
年级
一
二
三
四
五
六
人数
20
26
32
47
68
83
条形统计图
折线统计图
特点
用一个单位长度表示一定的数量
用直条的长短表
示数量的多少。
用折线起伏表示数量
的增减变化。
作用
从图中能清楚地
看出各数量的多
少,便于相互比
较。
从中能清楚地看出数量
的增减变化情况,也能
看出数量的多少。
例如:关于甲、乙两地月平均气温的
情况用复式折线统计图表示。
复式折线统计图的特点:
便于比较两种数据的变化趋势和差异性。
运用知识解决问题
(二)
1.选择
(1)心脏科要把病人的血压变化情况绘制成统计图,最佳选择是( )
A 条形统计图 B折线统计图
(2)要表示某校各班向灾区捐款情况,选用( )比较合适。
A 条形统计图 B折线统计图
第一单元
分数的意义和性质
分数
分数的意义
分数单位
分子分母的意义
分数与除法的关系
分数大小的比较
分数的分类
真分数
假分数
整数
带分数
分数的基本性质
约分
通分
求一个数是另一个数的几分之几
分数和小数的互化
表示把单位“1”平均分成 5 份,取其中 2 份。还表示把2平均分成5份,取其中1份。
表示 2 个 。
表示 2 除以 5 的商。
(分数的意义)
一个物体、一些物体等都可以看作一个整体,把这个整体平均分成若干份,这样的一份或几份都可以用分数来表示。
分数的意义
单位“1”表示:一个物体、一些物体等都可以看作一个整体,一个整体可以用自然数1来表示,通常把它叫做“1”。
分数单位表示:把单位“1”平均分成若干份,表示其中一份的数叫分数单位。
单位“1”与分数单位的区别
1.表示把单位“1”平均分成5份,取其中3份的分数是( ),它的分数单位是( ),再添上( )个这样的分数单位就是单位“1”。
2. 里面有( )个 。
( )里面有3个 。
3个 是( )。
3.比比两条线段哪个长?
1
3
1
4
4.写出数轴上点A、点B、点C、点D表示的分数
5.请在一条数轴上表示下列分数:
分数与除法的关系
工程队修一条5千米长的公路,7天修完,
(1)平均每天修这条公路的(——)千米;
(2)平均每千米要修(——)天;
(3)平均每天修的占这条公路的(——)。
大家有疑问的,可以询问和交流
可以互相讨论下,但要小声点
工程队修一条5千米长的公路,7天修完,
(1)平均每天修这条公路的(——)千米;
总千米 ÷ 总天数 = 每份数
5 ÷ 7 = (千米)
工程队修一条5千米长的公路,7天修完,
(2)平均每千米要修(——)天;
总天数 ÷ 总千米= 每份数
7 ÷ 5 = (天)
1
工程队修一条5千米长的公路,7天修完,
(3)平均每天修的占这条公路的(——)。
1 ÷ 7 =
工程队修一条5千米长的公路,7天修完,
(1)平均每天修这条公路的( )千米;
(2)平均每千米要修( )天;
(3)平均每天修的占这条公路的( )。
1
(4)把4米长的钢筋平均截成5段,
每段长( )米?
总米数 ÷ 总段数 =每份数
4 ÷ 5 = (米)
每段是钢筋全长的(——)
1 ÷ 5 =
(5)一个班有学生50人,其中13人被评为“三好学生”。“三好学生”占全班人数的(——)。
13 ÷ 50 =
小结:分数与除法的关系
分数可以表示整数除法的商,在表示整数除法时,要用除数作分母,用被除数作分子。
用关系式表示:
被除数÷除数= ————
用字母可以表示成:
a÷b= ——
因为除数不能等于“0”,所以b也不能等于“0”。
被除数
除数
a
b
分数与除法是有区别的。除法是一种运算,它有运算符号,是一个算式;而分数是一个“数”,当它在除法算式中的时候,它可以表示除法算式的结果。
小结:当一个量不能用整数个计量单位来表示时,可以用分数来表示。即分数可以表示一个量,分数还可以表示两个量之间的关系。
用分数表示下列除法算式的商。
6÷7=
11÷9=
15÷17=
a÷b=
下图是长方形,它的面积是5平方厘米。请你用阴影表示出
5
8
平方厘米的部分
5平方厘米
5平方厘米
5平方厘米的
1
8
5平方厘米
1平方厘米的
5
8
意义
特征
真分数
分子比分母小的分数
真分数小于1
假分数
分子比分母大或分子和分母相等的分数
假分数都大于或等于1
真分数和假分数
4 的分数单位是( ),去掉( )个
这样的分数单位就是最小的合数。
2
7
的分数单位是( ),再添( )
个这样的分数单位就是最小的质数。
7
8
在 中,a是不为0的自然数。
a
5
(真分数?假分数?最小假分数?最大真分数?)
填空
1.分数的基本性质
分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变。这叫做分数的基本性质。
2.约分
把一个分数化成和它相等,但分子、分母都比较小的分数,叫做约分。
3.通分
把异分母分数分别化成和原来分数相等的同分母分数,叫做通分。
4.最简分数
分子、分母只有公因数1的分数,叫做最简分数。
分数的基本性质
小结:分数的基本性质
约分是分数基本性质中的:分子、分母同时除以相同的数(0除外)的体现。
通分是分数基本性质中的:分子、分母同时乘上相同的数(0除外)的体现。
比较分数的大小除了用同分母、同分子和通分比较方法外,还可以灵活运用其它的方法。
占单位“1”的一半不够
占单位“1”的一半多
﹤
不用通分的方法,比较分数的大小。
因为 ﹥
所以(1— )﹤(1— )
﹤
将分数化为最简分数,可以将分子分母分别除以它们的最大公因数,也可以不断地约分,直到分子分母互质为止。
约分的技巧
分数 的分子加上8,要使分数
大小不变,分母应该( )。
0.6=( ) ÷25=
12
( )
3
5
或3÷5
一个分数的分子扩大20倍,分母缩小20倍,结果如何?
小数化分数,原来有几位小数就在1的后面写几个0做分母,把原来的小数去掉小数点作分子;
化成分数后,能约分的要约分。
分小互化
分小互化
分母是10、100、1000……的分数化小数,可以直接去掉分母,看分母中 1 后面有几个零,就在分子中从最后一位起向左数出几位,点上小数点。
分小互化
分母不是10、100、1000… …的分数化小数,要用分母去除分子;除不尽的,可以根据需要按四舍五入法保留几位小数。
1
2
1
4
2
5
3
4
1
5
1
8
4
5
3
5
3
8
5
8
7
8
1
20
1
16
3
16
5
16
7
16
1
25
1
50
1
40
把下面的分数化成小数,
并且记住这些结果。
3 2 3 1
20
9
5
8
3
3.025
0.16
0.15 0.2222…… 0.6 3.125
0.375
3
20
0.16
3.025
2
9
3
5
3
1
8
?
?
? ? ? ?
0.375
把下面各数按从小到大的顺序排列起来。
在( )里填上合适的分数
50厘米=( )米 250克=( )吨
45分= ( )时 400米=( )千米
600毫米=(— )米 40厘米= (— )米
15秒=( —)分 2500平方米=(— )公顷
50
100
1
2
1
4
3
4
2
5
1 1
4 4
3 2
5 5
互质数特殊的判断方法
① 1和任意自然数互质。
②2和任意奇数都是互质数。
③相邻两个自然数都是互质数。
④相邻的两个奇数都是互质数。
⑤不相同的两个质数是互质数。
⑥当一个数是合数,而另一个数是质数时,若合数不是质数的倍数,一般情况下这两个数也是互质数。
特殊情况
熟练掌握两种特殊情况。
两数关系
最大公因数
最小公倍数
互质关系
1
两数积
倍数关系
较小数
较大数
同时熟记7、11、13、17、19等数的倍数
及11—20所有数的平方数以提高计算速度。
求三个数的最小公倍数的特殊规律:
当三个数两两互质时,最小公倍数是这三个数的积; [2 ,7,9]= 126
当三个数都成整倍数关系时,最大的数就是最小公倍数; [18 ,6,54]= 54
当三个数中有两个数成倍数关系时,那么求三个数的最小公倍数就可转化为求这两个数中较大者与第三个数的最小公倍数等。
[18 ,6,27] [18 ,27]=108
第二单元 长方体和正方体
复习长方体和正方体
第一课时
长方形
正方形
三角形
按边分
按角分
等边三角形
等腰三角形
一般三角形
锐角三角形
直角角三角形
钝角三角形
平行四边形
梯形
等腰梯形
直角梯形
一般梯形
组合图形
平面图形
一、建构知识网络
立体图形
正方体
长方体
二、 注重知识的承接,回顾所学平面图形的特征、周长和面积公式。
名称
特征
周长(c)
面积(s)
长方形
两组对边分别平行且相等
(长+宽)×2
C=2(a+b)
长×宽
S=ab
正方形
四边相等
边长×4
C=4a
边长×边长
S=a?
平行四边形
两组对边平行且相等
底×高
S=ah
梯形
只有一组对边平行
(上底+下底)×高÷2
三角形
三条边,三个内角的和等于180°
(底×高)÷2
ah
S=
1
2
(a+b)h
S=
1
2
三、 明确长方体、正方体的异同。
从点、棱、面三方面比较长方体和正方体之间的相同点和不同点
长方体
正方体
相同点
6个面、12条棱、8个顶点
不同点
6个面都是长方形(有时相对的两个面是正方形),相对面完全相同。
6个面都是正方形,
6个面完全相同
相对棱的长度相等
12条棱长度都相等
正方体是特殊的长方体。
用集合图表示:
长方体
正方体
四、 复习长方体、正方体表面积的含义
15
10
8
后
前
上
下
左
右
●
15
10
8
单位:厘米
长方体六个面的面积,就是长方体的表面积。
1.长方体表面积的含义
2.正方体表面积的含义
(1)正方体棱长与每个面边长的关系
后
上
前
下
左
右
正方体展开图的每个面都是正方形,边长就是正方体的棱长,每个面的面积都等于棱长乘棱长。
(2)正方体的11种展开图。
图(1)
图(2)
图(3)
图(4)
图(5)
图(6)
第一类:中间四连方,两侧各有一个,共6种
第二类:中间三连方,一侧有一个、一侧有二个,共3种
图(7)
图(8)
图(9)
第三类:中间两连方,两侧各有2个,只有1种
图(10)
第四类:两排各有3个,只有1种
图(11)
五、复习长方体、正方体体积公式的推导
长方体的体积 = 长 × 宽 × 高
底面积
正方体的体积 = 棱长 ×棱长×棱长
底面积
可看作是高
长方体(或正方体)的
体积 = 底面积 × 高
六、体积与容积区别与联系
异同点
体积
容积
区别
意义不同
物体所占空间的大小,叫做物体的体积。
一个容器所能容纳物体的体积,叫做这个容器的容积。
测量方法不同
从物体外部测量长、宽、高。
从容器里面测量长、宽、高。
单位名称不同
m?、dm?、cm?。
容积单位:L和ml;计量固体时用体积单位。
联系
容积的大小是通过所能容纳物体的体积表示出来的。
计算方法相同
7厘米
5厘米
5厘米
这个长方体的长是( 7 )厘米,宽是( 5 )厘米,高是( 5 )厘米,这个长方体有( 2 )个面是正方形,有( 4 )个面是长方形。
如图
1.
2. 要焊接一个长10cm,宽8cm,高6cm的长方体框架,要准备10cm,宽8cm,高6cm的铁丝各( 4 )根。
3.一个正方体纸盒的棱长是7cm,这个纸盒的棱长总和是(84 )cm。
4.有一根150cm长的铁丝,用这根铁丝焊成了一个正方体的框架,还剩铁丝6cm。这个正方体框架的棱长是( )厘米。
七、基础知识的练习
150cm
12
8.有一个长方体,底面是一个正方形,高18cm,侧面展开正好是一个正方形。这个长方体的体积是( 364.5 ) cm? 。
18÷4=4.5(cm)
4.5×4.5×18
=20.25×18
=364.5(cm?)
18cm
18cm
18cm
10.把棱长是1厘米的小正方体拼摆在一起。如果从右面看,所看到的图形面积是( 7 )平方厘米,体积是( 11 )立方厘米。
11.
一个棱长为2cm的正方体,在它的一个角上挖掉一个棱长为1cm的小正方体,它的表面积是 (??? 24 )cm?。
第二课时:解决相关的实际问题
12cm
15cm
8cm
1. 一条彩带捆扎一种礼盒(如图),如果
接头处的彩带长30cm,求这条彩带的长度。
8×4+12×2+15×2+30=116(cm)
答:这条彩带长116厘米。
2.与右面正方体一致的展开图是( )。
B
1
2
3
1
2
3
2
3
1
1
2
3
C
B
A
甲
乙
取出石块后
2.1dm
1.8dm
3. 图中有两个完全一样的长方体水箱,水箱的底面积是2平方分米,请结合图中所给信息求出甲箱中石块的体积是多少?
2×(2.1-1.8)=0.6(dm?)
答:石块的体积是0.6dm?。
前
右
6
3
7
4.小明从一个长方体纸盒上撕下两个相邻的面(展开后如图,单位:厘米),这个纸盒的底面积是( )平方厘米,体积是( )立方厘米。
底面积:6×3=18(平方厘米)
18
126
体积:6×3×7=126(立方厘米)
5厘米
5厘米
5厘米
5.把 积木装入纸箱内,纸箱从里面量,长25厘米,宽和高都是20厘米。纸箱最多可容纳积木多少块?
(25÷5)×(20÷5)×(20÷5)
=5×4×4
=80(块)
答:纸箱最多可容纳积木80块。
6.把 积木装入纸箱内,纸箱从里面量,长25厘米,宽和高都是20厘米。纸箱最多可容纳积木多少块?
5厘米
3厘米
3厘米
(25÷3)×(20÷3)×(20÷5)
≈8×6×4
=192(块)
答:纸箱最多可容纳积木192块。
7.一块长方形铁皮,长40cm,宽30cm,像下图这样从4个角各剪掉一个边长为5厘米的正方形,然后做成盒子,这个盒子的容积是多少升?
40cm
30cm
(40-5×2)×(30-5×2)×5=3000(cm?)
3000cm?=3L
答:这个盒子的容积是3升。
12ml=12cm3 24ml=24cm3
一个小球的体积:(24-12) ÷(4-1)=4(cm3)
一个大球的体积:12-4=8(cm3)
左图长、宽、高分别是4cm、3cm、3cm。
它的体积是:
4×3×3=36(cm2)
右图长、宽、高分别是4cm、3cm、4cm。
它的体积是:
4×3×4=48(cm2)
10.用3个长5cm,宽4cm,高3cm的长方体木块,拼成一个表面积最小的长方体。这个长方体的表面积是多少平方厘米?
5cm
4cm
3cm
[5×4+5×(3×3)+4×(3×3)]×2=(20+45+36)×2=202(cm?)
答:这个长方体的表面积是202平方厘米。
3cm
2cm
6cm
6cm
11.有一个形状如图的零件,由一个长方体和一个
正方体组合而成。长方体的长和宽都是6cm,高是3cm,正方体的棱长是2cm。求这个零件的表面积。
2×2×4+6×3×4+6×6×2
=16+72+72
=160(cm?)
答:这个零件的表面积是160平方厘米。
12.由27个棱长为1cm的小正方体组成一个棱长为3cm的大正方体,若自上而下去掉中间的3个小正方体(如图所示),则剩下的几何体的表面积是多少平方厘米?
3×3×6-1×1×2+3×1×4
=54-2+12
=64(cm?)
答:剩下的几何体的表面积是64平方厘米。
13.从一个大长方体上切下一个体积是128立方厘米的小长方体(如图)。原来大长方体的体积是多少立方厘米?
22cm
8cm
切下部分
128÷8×22
=16×22
=352(立方厘米)
答:原来大长方体的体积是352立方厘米。
14. 一个密封的长方体容器里面装有一些水,水深9厘米,如果把这个容器的右面做底,这时容器内的水深多少厘米?
36
10
12
36
10
12
36×10×9=3240(cm3)
3240÷(12×10)=27(cm)
答:容器内的水深27厘米。
第三单元
分数的加法和减法
分数的加法和减法
分数加减法的简算
异分母分数加减法
同分母分数连减
同分母分数连加
同分母分数加减法
分数加减混合运算
异分母分数连加
异分母分数连减
同分母分数相加、减,分母不变,只把分子相加减。
1.同分母分数加减法
(1)同分母分数加法的意义及计算方法
(2)同分母分数减法的意义及计算方法
(3)同分母分数连加、连减
异分母分数加减法,先通分,转化为同分母分数进行计算。
2.异分母分数加减法
(1)异分母分数加法
(2)异分母分数减法
(3)分数加减法混合运算
a.不带括号的分数加减法混合运算
b.带括号的分数加减法混合运算
加法的运算定律和减法的性质同样适应于分数中的计算。
2
7
+
3
7
3
8
+
1
8
5
12
-
3
12
4
9
-
2
9
25
36
-
17
36
-
5
36
9
11
-
1.口算
-
7
11
2
11
注意化简和简算
异分母分数加减法,先通分,转化为同分母分数进行计算。
2.计算
加法的运算定律和减法的性质同样适应于分数中的计算。
1
2
+
1
3
1
3
+
1
7
1
5
-
1
8
1
9
-
1
16
先计算下面各题,想一想怎样计算比较快?
用字母表示为:
1
a
±
1
b
=
b±a
ab
a、b均不为0
1
2
1
4
1
8
1
16
1
32
+
+
+
+
1
32
1
4
1
8
1
16
1
2
1
2
1
4
1
8
1
16
1
32
+
+
+
+
拆项法:
1
2
=
1
-
+
1
2
-
1
4
+
1
4
-
1
8
+
1
8
-
+
1
16
-
1
32
1
16
=
=
1
1
32
-
31
32
学校图书馆有故事书占图书总数的 ,
工具书占总数的 ,
剩下的是科技书,科技书占总数的 几分之几?
1- -
=
-
-
=
答:科技书占总数的 。
在圆圈内填上适当的分数,使每行、每列的三个数加起来的和都等于1。
八.比例问题
1.甲乙两人在河边钓鱼,甲钓了三条,乙钓了两条,正准备吃,有一个人请求跟他们一起吃,于是三人将五条鱼平分了,为了表示感谢,过路人留下10元,甲、乙怎么分?
解:“三人将五条鱼平分,客人拿出10元”,可以理解为五条鱼总价值为30元,那么每条鱼价值6元。又因为“甲钓了三条”,相当于甲吃之前已经出资3*6=18元,“乙钓了两条”,相当于乙吃之前已经出资2*6=12元。而甲乙两人吃了的价值都是10元,所以甲还可以收回18-10=8元乙还可以收回12-10=2元刚好就是客人出的钱。
认真思考
2.一种商品,今年的成本比去年增加了10分之1,但仍保持原售价,因此,每份利润下降了5分之2,那么,今年这种商品的成本占售价的几分之几?
最好画线段图思考:把去年原来成本看成20份,利润看成5份,则今年的成本提高1/10,就是22份,利润下降了2/5,今年的利润只有3份。增加的成本2份刚好是下降利润的2份。售价都是25份。所以,今年的成本占售价的22/25。
简易方程
整理与复习
简易方程
用字母表示确定的数
和不确定的数
用字母表示运算定律
用字母表示计算公式
用字母表示数量关系
方程的意义
解方程
稍复杂的方程
用字母表示数
解简易方程
列方程解决问题
基本的方程
方程
方程的解
解方程
一、用字母表示数
用含有字母的式子表示数、数量关系、公式和定律等。
路程(s)、速度(v)、时间(t)的数量关系:
s=vt v=s÷t t=s÷v
总价(c)、数量(x)、单价(a)的数量关系:
c=ax a=c÷x x=c÷a
运算定律:
a+b=b+a (a+b)+c=a+(b+c)
ab=bc (ab)c=a(bc) (a+b) c=ac+bc
工作总量(c)、工作时间(t)、工作效率(a)的数量关系:
c=at a=c÷t t=c÷a
计算公式:
S =ab C =(a+b)X2
S =a﹒a C =4a
S =ah S =ah÷2
S =(a+b)h÷2
复习:小轿车的速度是a千米/小时,它从广州开往惠州,行了1.5小时后距离惠州还有32千米。
(1)1.5a表示( ? );广州距离惠州有( )千米。
(2)当a=90时,计算广州到惠州的路程。
时间
速度
X
=路程
1.5小时行的路程
总距离
1.5小时行的路程
32千米
1.5a+32
广州
惠州
1.5a+32
= 1.5X90+32
=135+32
167(千米)
一、用字母表示数
1.一个平行四边形的底是a厘米,高3厘米,它的面积是( )平方厘米。
巩固练习---在括号里填上含有字母的式子。
S =ah
=3a
3.小英重n千克,比小华轻3千克,小华体重是( )千克。
C =(a+b )X2
=(48+b)X2
=96+2b
2.一个长方形的长是48分米,宽是b分米,它的周长是( )分米。
一、用字母表示数
小华
比小英重3千克
3a
96+2b
3+n
6.一头奶牛一天可以产奶y千克,6头奶牛一周可以产奶( )千克。
5.学校美术组有X人,体育组的人数是美术组人数的4倍,体育组有( )人。当X=15时,体育组有( )人。
巩固练习---在括号里填上含有字母的式子。
4.汽车平均每小时行m千米,6小时能行( )千米,行450千米要( )小时。
S=vt
=6m
4x=4×15=60
6m
4x
t=S÷v
=450÷m
450÷m
60
工作总量=工作效率 ×工作时间(C=at )
一头奶牛一周的产奶总量= y×7
6头奶牛一周的产奶总量= y×7×6=42y
42y
一、用字母表示数
①当字母与数字相乘时,去掉乘号,把数字写在字母的前面,也可以用点表示乘号,如:a×3通常可以写成3a或3·a。
②当字母与字母相乘时,省略乘号,用点表示或直接去掉乘号,如:a×b写成a·b或ab;(通常按字母的先后顺序写)
③字母与1相乘省略1不写,只写字母本身,如:1×a写成a。
④两个一样的字母相乘就写一个字母,再在字母的右上角写上2,如:a×a通常写成a·a或a2,读作:a的平方。
1.含字母的乘法算式的简写的规则
一、用字母表示数
2.练习
A.填空。
(1)图书角原来有X本书,被同学借走10本后还有( )本。
(2)小芳今年Y岁,妈妈年龄是小芳的6倍,妈妈今年( )岁。
(3)一个正方形的边长是A分米,它的面积是( )平方分米。
(4)公交车上原有w人,到站后下车8人,上车k人,现在车上有( )人。
(5)小明的妈妈今年37岁,比小明大A岁,小明今年( )岁,过30年后妈妈比小明大( )岁。
(6)用a表示长方形的长,用b表示它的宽。
它的面积公式为: 。
它的周长公式为: 。
S=ab
C=(a+b)×2
C=2(a+b)
X-10
6Y
A?
W-8+K
A
37-A
(7)乘法结合律、乘法分配律分别用字母表示
abc=a(bc)
a(b+c)=ab+ac
B.做一做:书本p120第3题。
请你用字母表示下面的数量关系。
王叔叔每小时加工a个零件,t小时共加工c个零件。
(1)如果每小时加工30个零件,5小时可以加工( )零件。
(2)如果每小时加工25个零件,( )小时可以加工100个零件。
C=at
a=C÷t
t=C÷a
150
4
(1)等式的意义:表示等号两边是相等关系的式子叫等式。
二、方程的概念
如:3+6.5=9.5、 3.6× 0.5=1.8、 3.5+x=9.5等都是等式。
(2)方程的意义:
如: x + 3.2=8、 11x=363、x÷7.6=11.4等都是方程。
3x+1>5 、 x-12.5﹤5 3+6.5=9.5等不是方程。
(3)方程与等式的关系:
如:35 ÷7=5、2x=0、 3.5x=4、11.2-x=11.14等都是等式,
但 35÷ 7=5 不是方程。
含有未知数的等式叫方程。
等式的范围比方程的范围大。
方程都是等式,但等式不一定是方程。
等式的性质:
等式两边同时加上(减去)一个数,左右两边仍然相等;
等式两边同时乘或除以一个(不为0)的数,左右两边仍然相等。
二、方程的概念
巩固练习----判断。
1、等式不一定是方程,方程一定是等式。 ( )
2、因为100-25x,含有未知数x,所以它是方程。 ( )
3、含有未知数的算式叫做方程?.?? ????????? (? ?)
???????????????????
(3x+1>5不是方程)
(100-25x=0 ?)?
(等式的范围比方程的范围大。)
√
×
×
方程的意义
1、什么叫方程?
2、方程的条件有哪些?
3、什么叫方程的解?
4、什么叫解方程?
方程的解实际上是 .
一个数
一个过程
解方程实际上是 .
未知数、等式
含有未知数的等式.
使方程左右两边相等的未知数的值,叫做方程的解
求方程的解的过程叫做解方程
2.练一练:将序号填入圈中。
⑴ 30+2=32 ⑵ 3×X ⑶ X-T=6
⑷ 4+A>18 ⑸ 25÷v=Z ⑹ 5.6-4=G
方程
等式
不是等式
⑵
⑶
⑷
⑸
⑹
⑴
⑶
⑸
⑹
方程与等式之间的关系
等 式
方程一定是等式;
但等式不一定是方程。
方程
简易方程
整理与复习
解方程的原理是什么?要注意什么?
(1)等式的两边同时加上或减去相同的数,等式不变。
(2)等式的两边同时乘或除以相同的数(0除外),等式不变。
同加同减
同乘同除
3.解方程(打★写出检验过程)
5(X-1.5)=17.5
4X-1.2X=4.2
解:
★
5(X-1.5)÷5=17.5÷5
X-1.5=3.5
X-1.5+1.5=3.5+1.5
X=5
检验:方程左边=
5(X-1.5)
=5×(5-1.5)
=17.5
=5×3.5
=方程右边
所以,X=5是方程的解。
解:
(4-1.2)X=4.2
2.8X=4.2
2.8X÷2.8=4.2÷2.8
X=1.5
χ-12=30
у+12=42
6χ=30
χ÷5=30
解:χ-12+12=30+12
解:у+12-12=42-12
解:6χ÷6=30÷6
解:χ÷5×5=30×5
χ=42
у=30
χ=5
χ=150
χ-12=30
у+12=42
6χ=30
χ÷5=30
6χ+12=42
解:6χ+12-12=42-12
6χ=30
6χ÷6=30÷6
χ=5
6χ+2×6=42
解:6χ+12=42
6χ+12-12=42-12
6χ=30
6χ÷6=30÷6
χ=5
6(χ+2)=42
解:6(χ+2)÷6=42÷6
χ+2=7
χ+2-2=7-2
χ=5
5χ+χ=30
解:6χ=30
6χ÷6=30÷6
χ=5
6χ+12=42
解:6χ+1 2-12=42-12
6χ=30
6χ÷6=30÷6
χ=5
6χ+2×6=42
解:6χ+12=42
6χ+12-12=42-12
6χ=30
6χ÷6=30÷6
χ=5
6(χ+2)=42
解:6(χ+2)÷6=42÷6
χ+2=7
χ+2-2=7-2
χ=5
5χ+χ=30
解:6χ=30
6χ÷6=30÷6
χ=5
解:6χ=42-12
χ=30÷6
6χ=42-12
χ=30÷6
χ=30÷6
解:χ+2=42÷6
χ=7-2
刚才这些方程可不可以简化解方程的过程?
三.解方程
x+5=12.3 x-6=9.2 4x=24.8 x÷2=16.2
解方程的依据---等式的性质。
方程两边同时加上(减去)一个数,左右两边仍然相等;
方程两边同时乘或除以一个(不为0)的数,左右两边仍然相等。
1.简单方程:
-5
-5
+6
+6
÷4
÷4
×2
×2
解:
x=12.3- 5
x=7.3
解:
x=9.2 +6
x=15.2
解:
x=24.8 ÷4
x=6.2
解:
x=16.2 ×2
x=32.4
三.解方程
(1)1.2x-4.4=5.6×2
解复杂方程的要点:
1、能计算的要先算.
2、把和X在一起或较近的数看作一个整体.
2.复杂方程:
把1.2X看作是一个整体,先算5.6×2 .
+4.4
+4.4
解:
1.2x-4.4= 11.2
1.2x=11.2+4.4
1.2x=15.6
x=15.6÷1.2
÷1.2
÷1.2
x=13
三.解方程
(2) 2.7X+0.9X=1.44
2.复杂方程:
先算2.7X+0.9X.
解:
3.6x= 1.44
x = 1.44÷3.6
÷3.6
÷3.6
x = 0.4
解复杂方程的要点:
1、能计算的要先算.
2、把和X在一起或较近的数看作一个整体.
三.解方程
(3)0.6(x÷8)=0.9
2.复杂方程:
把x÷8 看作是一个整体.
解:
x÷8 = 0.9÷0.6
x÷8 = 1.5
÷0.6
÷0.6
x = 1.5×8
×8
×8
x = 12
验算:方程左边=0.6×(12÷8) =0.9=右边
所以, X = 12是原方程的解。
解简易方程
X+7.8=20.2 x-6=12.5
5X=20.5 x÷6=18.6
5.6 X-8.6=19.4
2 X+1.2×5=7
3.2 X-1.5 X=0.51
(4.5+X)×2=13
简易方程
整理与复习
说说列方程解应用题的步骤:
1、读题(至少读3遍),弄清题目中的数量关系。
2、写出等量关系式。能用线段图最好
3、找出等量关系式中的未知数,设为X。
4、根据等量关系式列出方程。
5、解方程。
6、检验。
列方程解应用题
A.说出下面各题中数量之间的相等关系。
(1)养禽场一共养鸡鸭600只。
(2)红花比黄花少25朵。
(3)参加航模组的人数是参加美术组的3倍。
(4)花金鱼比黑金鱼的1.2倍还多8条。
2.练习:
鸡的只数+鸭的只数=一共养的只数
黄花的数量-25朵=红花的数量
一共养的只数-鸡的只数=鸭的只数
黄花的数量-红花的数量=25朵
红花的数量+25朵=黄花的数量
一共养的只数-鸭的只数=鸡的只数
参加美术组的人数×3=参加航母组的人数
参加航母组的人数÷参加美术组的人数=3
参加航母组的人数÷3=参加美术组的人数
黑金鱼的条数×1.2+8=花金鱼的条数
B. 列方程解决问题。
(1)桔树有150棵,比梨树多30棵,梨树有几棵?
(2)桔树有150棵,是梨树的3倍,梨树有几棵?
(3)桔树有150棵,比梨树的3倍还多30棵,梨树有几棵?
(5)桔树和梨树共有150棵,桔树棵数是梨树的2倍, 桔树和梨树各有几棵?
(4)果园运来25捆桔树和梨树,共150棵,已知每捆桔树4棵,每捆梨树有几棵?
解:设梨树有X棵。
梨树棵数+30棵=桔树棵数
x+30=150
解:设梨树有X棵。
梨树棵数×3=桔树棵数
3X=150
解:设梨树有X棵。
梨树棵数×3+30=桔树棵数
3X+30=150
解:设梨树有X棵。
桔树棵数+梨树棵数=150棵
25×4+25X=150
解:设梨树有X棵,那么桔树有2X棵。
2X+X=150
桔树棵数+梨树棵数=150
有两个书架,第一个书架书的本数是第二个的1.5倍。如果从第一个书架取出50本放入第二个中,则两个书架的数就一样多。原来两个书架各有几本书?
解:设第二个书架有x本书,那么第一个书架有1.5x本书。
两个书架相差了(50×2)本
1.5x-x= 50×2
0.5x= 100
第一个书架书的本数-第二个书架书的本数=相差的本数
0.5x÷0.5= 100÷0.5
x= 200
第一个书架:1.5x=1.5×200=300
不写单位
2.有两个书架,第一个书架书的本数是第二个的1.5倍。如果从第一个书架取出50本放入第二个中,则两个书架的数就一样多。原来两个书架各有几本书?
解:设第二个书架有x本书,那么第一个书架有1.5x本书。
1.5x-50= x+50
第一个书架书的本数-50=第二个书架书的本数+50
0.5x-50= 50
第一个书架:1.5x=1.5×200=300
不写单位
1.5x-50-X= x+50-X
0.5x-50+50= 50+50
0.5x= 100
0.5x÷0.5=100÷0.5
x=200
复习一:少年宫合唱队有84人,合唱队的人数比舞蹈队的3倍多15人。舞蹈队有多少人?
舞蹈队人数:
合唱队人数:
X
3X
15
84
想:根据题意,舞蹈队人数的3倍加上15,正好等于合唱队的人数。
解:设舞蹈队有x人。
3X+15=84
3X+15-15=84-15
3X÷3=69÷3
X=23
答:舞蹈队有23人。
复习二:兴华服装厂五月份做大人服装1500套,做的儿童服装比大人服装的3倍少270套。做儿童服装多少套?
大人服装:
儿童服装:
1500
3
270
X
想:根据题意,儿童服装的套数加上270套再除以3正好是大人服装的套数。
解:设做儿童服装X套。
(x+270) ÷3=1500
(X+270) ÷3×3=1500×3
x+270=4500
X+270-270=4500-270
X=4230
答:做儿童服装4230套。
复习三:果园里一共种了340棵桃树和杏树,其中桃树的棵数比杏数的3倍多20棵。两种树各种了多少棵?
杏树的棵数:
桃树的棵数:
X
X
X
X
多20
3X+20
想:这道题要求两个未知数。我们可以先设其中一个未知数为X,根据题意列方程解答,然后再求出另一个未知数。
解:设杏树有X棵。那么桃树有3X+20棵
340
X+3X+20=340
4X+20-20=340-20
4X=320
4X÷4=320÷4
X=80
3X+20=3×80+20
=260
答:杏树有80棵,桃树有260棵。
复习四:有两袋大米,甲袋大米的重量是乙袋的1.2倍。如果再往乙袋里装5千克大米,两袋就一样重了。原来两袋大米各有多少千克?
甲袋:
乙袋:
想:设乙袋有X千克,则甲袋就有1.2X千克,甲袋大米的重量减去乙袋大米的重量刚好等于再往乙袋装的5千克大米。
解: 设乙袋有X千克大米,那么,甲袋有1.2X千克大米。
X
1.2X
5
1.2X-X=5
0.2X=5
0.2X÷0.2=5÷0.2
X=10
1.2X=1.2×10=12
答:原来甲袋大米有12千克,乙袋大米有10千克。
2、妈妈有200元钱,是小红的4倍多20元,小红有多少元?
3、爸爸的年龄比儿子大32岁,是儿子年龄的9倍,爸爸和儿子各多少岁?
4、学校买10套课桌用500元,已知桌子的单价是凳子的4倍,每张桌子多少元?
1、苹果树和梨树共有270棵,苹果树棵数是梨树的2倍, 桔树和梨树各有几棵?
统计与概率
表三:单式折线统计图
表三 光明小学一----六年级喜欢看科普读物人数统计表
年级
一
二
三
四
五
六
人数
20
26
32
47
68
83
条形统计图
折线统计图
特点
用一个单位长度表示一定的数量
用直条的长短表
示数量的多少。
用折线起伏表示数量
的增减变化。
作用
从图中能清楚地
看出各数量的多
少,便于相互比
较。
从中能清楚地看出数量
的增减变化情况,也能
看出数量的多少。
例如:关于甲、乙两地月平均气温的
情况用复式折线统计图表示。
复式折线统计图的特点:
便于比较两种数据的变化趋势和差异性。
运用知识解决问题
(二)
1.选择
(1)心脏科要把病人的血压变化情况绘制成统计图,最佳选择是( )
A 条形统计图 B折线统计图
(2)要表示某校各班向灾区捐款情况,选用( )比较合适。
A 条形统计图 B折线统计图
