回归分析的基本思想及其初步应用
文档属性
| 名称 | 回归分析的基本思想及其初步应用 |  | |
| 格式 | zip | ||
| 文件大小 | 271.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-10 22:07:45 | ||
图片预览








文档简介
(共39张PPT)
第一章 统计案例
a. 比《数学3》中“回归”增加的内容
数学3——统计
画散点图
了解最小二乘法的思想
求回归直线方程
y=bx+a
用回归直线方程解决应用问题
选修1-2——统计案例
引入线性回归模型
y=bx+a+e
了解模型中随机误差项e产生的原因
了解相关指数 R2 和模型拟合的效果之间的关系
了解残差图的作用
利用线性回归模型解决一类非线性回归问题
正确理解分析方法与结果
问题1:正方形的面积y与正方形的边长x之间
的函数关系是
y = x2
确定性关系
问题2:某水田水稻产量y与施肥量x之间是否 -------有一个确定性的关系?
例如:在 7 块并排、形状大小相同的试验田上 进行施肥量对水稻产量影响的试验,得到如下所示的一组数据:
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
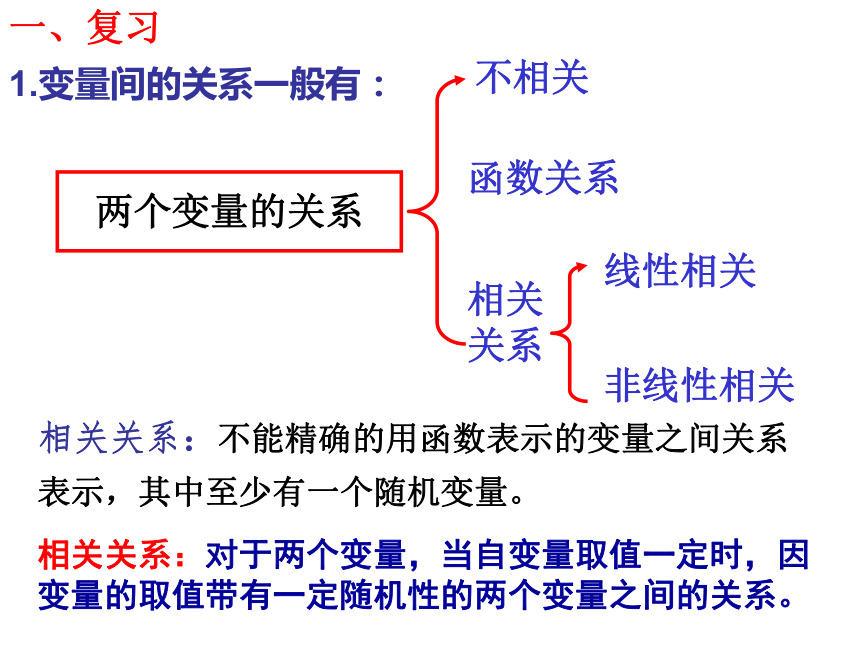
复习、变量之间的两种关系
两个变量的关系
不相关
相关关系
函数关系
线性相关
非线性相关
相关关系:对于两个变量,当自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系。
1.变量间的关系一般有:
一、复习
相关关系:不能精确的用函数表示的变量之间关系
表示,其中至少有一个随机变量。
2.回归分析 :研究一个随机变量(因变量)与几个可
控变量(自变量)之间的相关关系。根据自变量的个
数又可分为一元及多元回归分析。
一、复习
3.对两个具有线性相关关系的变量进行回归分析的步骤:
1).画散点图;
2).求回归直线方程
3).用回归直线方程进行预报.
问题:对于线性相关的两个变量用什么方法来刻划之间的关系呢?
最小二乘法估计
最小二乘法估计下的线性回归方程:
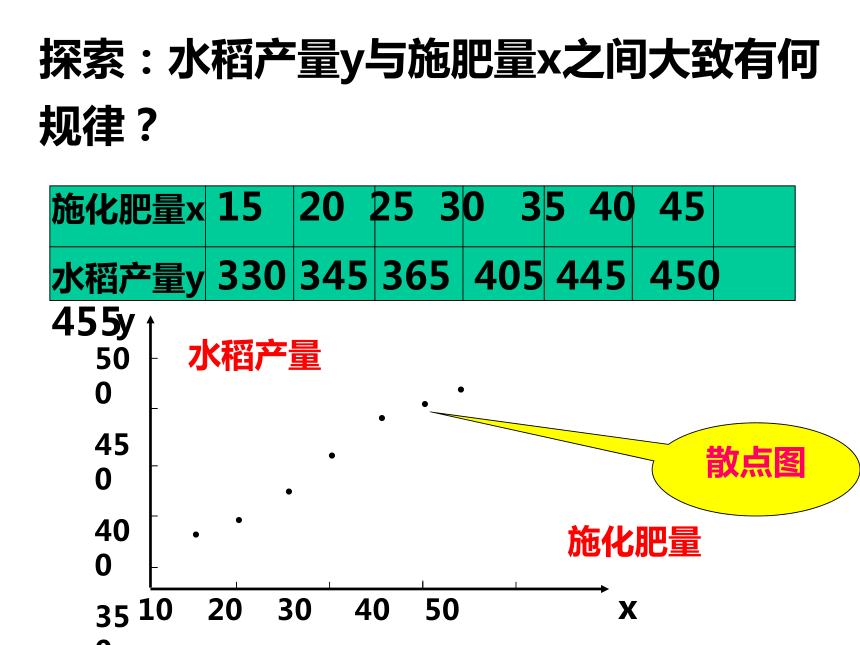
探索:水稻产量y与施肥量x之间大致有何规律?
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
10 20 30 40 50
500
450
400
350
300
·
·
·
·
·
·
·
x
y
施化肥量
水稻产量
散点图
10 20 30 40 50
500
450
400
350
300
·
·
·
·
·
·
·
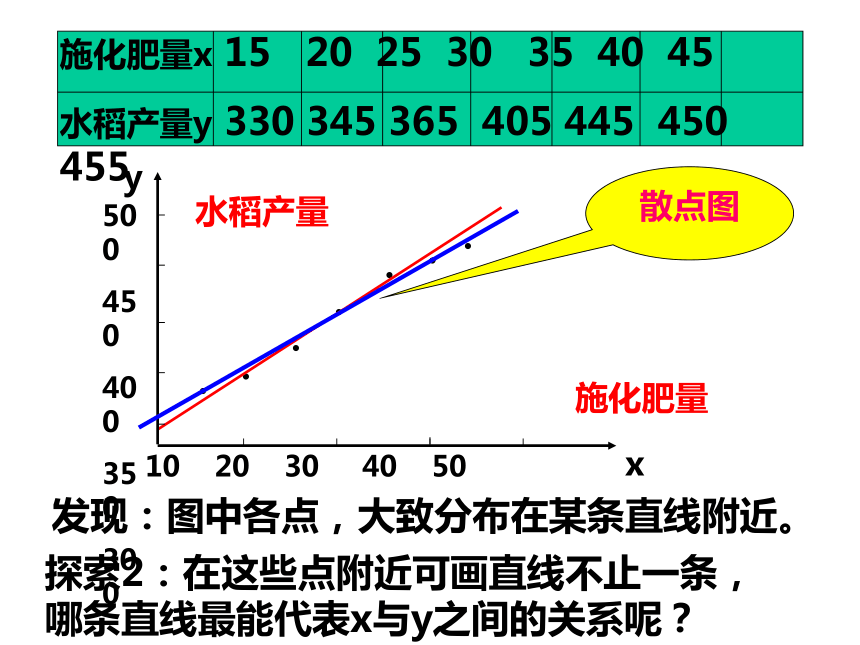
发现:图中各点,大致分布在某条直线附近。
探索2:在这些点附近可画直线不止一条, 哪条直线最能代表x与y之间的关系呢?
x
y
施化肥量
水稻产量
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
散点图
在Y与X的散点图上画出直线的方法很多。找出一条能够最好地描述Y与X(代表所有点)之间的直线。
最小二乘法的思路
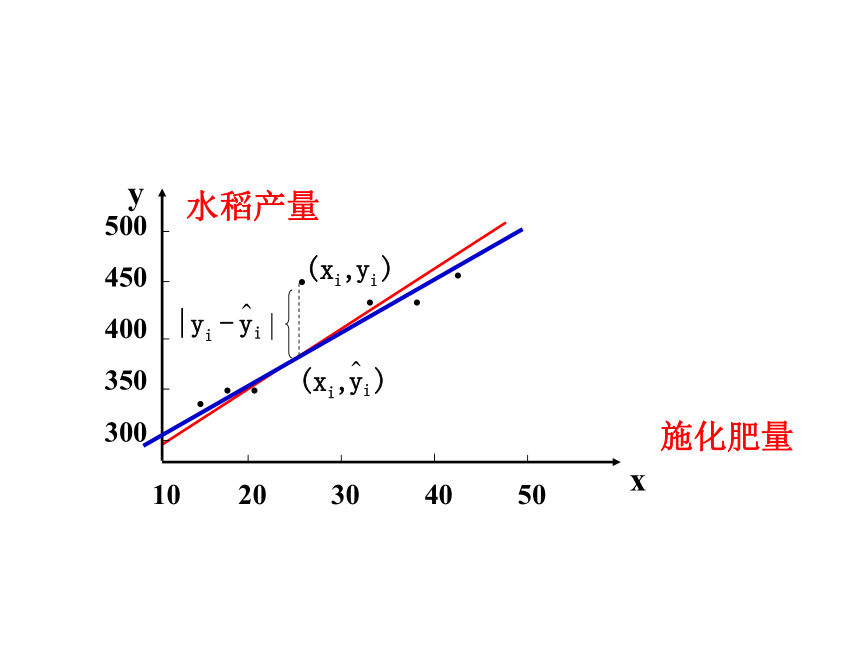
问题是:怎样算“最好”?
最好指的是找一条直线使得所有这些点到该直线的纵向距离的和(平方和)最小。
10 20 30 40 50
500
450
400
350
300
·
·
·
·
·
·
·
x
y
施化肥量
水稻产量
求回归方程的方法:
用最小二乘法,其截距和斜率的估计公式为
例题1 从某大学中随机选出8名女大学生,其身高和体重数据如下表:
编号 1 2 3 4 5 6 7 8
身高 165 165 157 170 175 165 155 170
体重 48 57 50 54 64 61 43 59
求根据一名女大学生的身高预报她的体重的回归方程,并预报一名身高为172cm的女大学生的体重。
1.画散点图
身高
体重
2、由散点图知道身高和体重有比较好的线性相关关系,因此可以用线性回归方程刻画它们之间的关系。
3.求出截距和斜率:
1.画散点图
身高
体重
4.得出回归方程:
5.预报身高172女生体重:
探究P4:
身高为172cm的女大学生的体重一定是60.316kg吗?如果不是,你能解析一下原因吗?
(2)从散点图还可以看到,样本点散布在某一条直线的附近,而不是一条直线上,所以不能用一次函数y=bx+a来描述它们之间的关系。这时我们用下面的线性回归模型来描述身高和体重的关系:y=bx+a+e其中a和b为模型的未知参数,e是y与 之间的误差,通常e称为随机误差。
思考P4
产生随机误差项e的原因是什么?
随机误差e的来源(可以推广到一般):
1、其它因素的影响:影响身高 y 的因素不只是体重 x,可能 还包括遗传基因、饮食习惯、生长环境等因素;
2、用线性回归模型近似真实模型所引起的误差;
3、身高 y 的观测误差。
函数模型与回归模型之间的差别
函数模型:
回归模型:
可以提供
选择模型的准则
函数模型与回归模型之间的差别
函数模型:
回归模型:
线性回归模型y=bx+a+e增加了随机误差项e,因变量y的值由自变量x和随机误差项e共同确定,
即自变量x只能解释部分y的变化。
在统计中,我们也把自变量x称为解释变量,因变量y称为预报变量。
假设身高和随机误差的不同不会对体重产生任何影响,那么所有人的体重将相同。
在体重不受任何变量影响的假设下,设8名女大学生的体重都是她们的平均值,即8个人的体重都为54.5kg。
54.5
54.5
54.5
54.5
54.5
54.5
54.5
54.5
体重/kg
170
155
165
175
170
157
165
165
身高/cm
8
7
6
5
4
3
2
1
编号
编号 1 2 3 4 5 6 7 8
身高 165 165 157 170 175 165 155 170
体重 48 57 50 54 64 61 43 59
54.5kg
在散点图中,所有的点应该落在同一条水平直线上,但是观测到的数据并非如此。
这就意味着预报变量(体重)的值受解释变量(身高)或随机误差的影响。
编号 1 2 3 4 5 6 7 8
身高 165 165 157 170 175 165 155 170
体重 48 57 50 54 64 61 43 59
59
43
61
64
54
50
57
48
体重/kg
170
155
165
175
170
157
165
165
身高/cm
8
7
6
5
4
3
2
1
编号
例如,编号为6的女大学生的体重并没有落在水平直线上,她的体重为61kg。解析变量(身高)和随机误差共同把这名学生的体重从54.5kg“推”到了61kg,相差6.5kg,所以6.5kg是解释变量和随机误差的组合效应。
用这种方法可以对所有预报变量计算组合效应。
数学上,把每个效应(观测值减去总的平均值)的平方加起来,
即用 表示总的效应,称为总偏差平方和。
在例1中,总偏差平方和为354。
59
43
61
64
54
50
57
48
体重/kg
170
155
165
175
170
157
165
165
身高/cm
8
7
6
5
4
3
2
1
编号
那么,在这个总的效应(总偏差平方和)中,有多少来自于解析变量(身高)?有多少来自于随机误差?
假设随机误差对体重没有影响,也就是说,体重仅受身高的影响,那么散点图中所有的点将完全落在回归直线上。但是,在图中,数据点并没有完全落在回归
直线上。
这些点散布在回归直线附近,所以一定是随机误差把这些点从回归直线上“推”开了。
因此,数据点和它在回归直线上相应位置的差异 是随机误差的效应,称 为残差。
59
43
61
64
54
50
57
48
体重/kg
170
155
165
175
170
157
165
165
身高/cm
8
7
6
5
4
3
2
1
编号
在例1中,残差平方和约为128.361。
例如编号为6的女大学生计算随机误差的效应(残差)为:
对每名女大学生计算这个差异,然后分别将所得的值平方后加起来,用数学符号表示为:
称为残差平方和,它代表了随机误差的效应。
因此,数据点和它在回归直线上相应位置的差异 是随机误差的效应,称 为残差。
由于解释变量和随机误差的总效应(总偏差平方和)为354,而随机误差的效应为128.361,所以解释变量的效应为
解释变量和随机误差的总效应(总偏差平方和)
=解释变量的效应(回归平方和)
+随机误差的效应(残差平方和)
354-128.361=225.639
这个值称为回归平方和。
离差平方和的分解
(三个平方和的意义)
总偏差平方和(SST)
反映因变量的 n 个观察值与其均值的总离差
回归平方和(SSR)
反映自变量 x 的变化对因变量 y 取值变化的影响,或者说,是由于 x 与 y 之间的线性关系引起的 y 的取值变化,也称为可解释的平方和
残差平方和(SSE)
反映除 x 以外的其他因素对 y 取值的影响,也称为不可解释的平方和或剩余平方和
我们可以用相关指数R2来刻画回归的效果,其计算公式是
我们可以用相关指数R2来刻画回归的效果,其计算公式是
显然,R2的值越大,说明残差平方和越小,也就是说模型拟合效果越好。
在线性回归模型中,R2表示解释变量对预报变量变化的贡献率。
R2越接近1,表示回归的效果越好(因为R2越接近1,表示解释变量和预报变量的线性相关性越强)。
我们可以用相关指数R2来刻画回归的效果,其计算公式是
如果某组数据可能采取几种不同回归方程进行回归分析,则可以通过比较R2的值来做出选择,即选取R2较大的模型作为这组数据的模型。
总的来说:
相关指数R2是度量模型拟合效果的一种指标。
在线性模型中,它代表自变量刻画预报变量的能力。
1
354
总计
0.36
128.361
残差变量
0.64
225.639
解释变量
比例
平方和
来源
表1-3
从表1-3中可以看出,解释变量对总效应约贡献了64%,即R2 0.64,
可以叙述为“身高解析了64%的体重变化”,而随机误差贡献了剩余的36%。
所以,身高对体重的效应比随机误差的效应大得多。
下表列出了女大学生身高和体重的原始数据以及相应的残差数据。
残差分析与残差图的定义:
我们可以通过残差 来判断模型拟合的效果,判断原始数据中是否存在可疑数据,这方面的分析工作称为残差分析。
编号 1 2 3 4 5 6 7 8
身高/cm 165 165 157 170 175 165 155 170
体重/kg 48 57 50 54 64 61 43 59
残差 -6.373 2.627 2.419 -4.618 1.137 6.627 -2.883 0.382
我们可以利用图形来分析残差特性,作图时纵坐标为残差,横坐标可以选为样本编号,或身高数据,或体重估计值等,这样作出的图形称为残差图。
残差图的制作及作用。
坐标纵轴为残差变量,横轴可以有不同的选择;
若模型选择的正确,残差图中的点应该分布在以横轴为心的带形区域;
对于远离横轴的点,要特别注意。
身高与体重残差图
异常点
错误数据
模型问题
几点说明:
第一个样本点和第6个样本点的残差比较大,需要确认在采集过程中是否有人为的错误。如果数据采集有错误,就予以纠正,然后再重新利用线性回归模型拟合数据;如果数据采集没有错误,则需要寻找其他的原因。
另外,残差点比较均匀地落在水平的带状区域中,说明选用的模型计较合适,这样的带状区域的宽度越窄,说明模型拟合精度越高,回归方程的预报精度越高。
1)确定解释变量和预报变量;
2)画出散点图;
3)确定回归方程类型;
4)求出回归方程;
5)利用相关指数或残差进行分析.
建立回归模型的基本步骤
例2:一只红铃虫的产卵数y与温度x有关,现收集了7组观测数据,试建立y与x之间的回归方程
解:1)作散点图;
从散点图中可以看出产卵数和温度之间的关系并不能用线性回归模型来很好地近似。这些散点更像是集中在一条指数曲线或二次曲线的附近。
解: 令
则z=bx+a,(a=lnc1,b=c2),列出变换后数据表并画 出x与z 的散点图
x和z之间的关系可以用线性回归模型来拟合
x 21 23 25 27 29 32 35
z 1.946 2.398 3.045 3.178 4.19 4.745 5.784
2) 用 y=c3x2+c4 模型,令 ,则y=c3t+c4 ,列出变换后数据表并画出t与y 的散点图
散点并不集中在一条直线的附近,因此用线性回归模型拟合他们的效果不是最好的。
t 441 529 625 729 841 1024 1225
y 7 11 21 24 66 115 325
残 差 表
编号 1 2 3 4 5 6 7
x 21 23 25 27 29 32 35
y 7 11 21 24 66 115 325
e(1) 0.52 -0.167 1.76 -9.149 8.889 -14.153 32.928
e(2) 47.7 19.397 -5.835 -41.003 -40.107 -58.268 77.965
非线性回归方程
二次回归方程
残差公式
方法:把非线性的回归问题化为线性问题来考虑,
通过变换来实现。
(1)根据数据,作散点图 ;
(2)由经验确定回归方程的类型(如观察到数据呈
线性关系,则选用线性回归方程y=bx+a) ;
(3)若呈指数关系,则设为
第一章 统计案例
a. 比《数学3》中“回归”增加的内容
数学3——统计
画散点图
了解最小二乘法的思想
求回归直线方程
y=bx+a
用回归直线方程解决应用问题
选修1-2——统计案例
引入线性回归模型
y=bx+a+e
了解模型中随机误差项e产生的原因
了解相关指数 R2 和模型拟合的效果之间的关系
了解残差图的作用
利用线性回归模型解决一类非线性回归问题
正确理解分析方法与结果
问题1:正方形的面积y与正方形的边长x之间
的函数关系是
y = x2
确定性关系
问题2:某水田水稻产量y与施肥量x之间是否 -------有一个确定性的关系?
例如:在 7 块并排、形状大小相同的试验田上 进行施肥量对水稻产量影响的试验,得到如下所示的一组数据:
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
复习、变量之间的两种关系
两个变量的关系
不相关
相关关系
函数关系
线性相关
非线性相关
相关关系:对于两个变量,当自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系。
1.变量间的关系一般有:
一、复习
相关关系:不能精确的用函数表示的变量之间关系
表示,其中至少有一个随机变量。
2.回归分析 :研究一个随机变量(因变量)与几个可
控变量(自变量)之间的相关关系。根据自变量的个
数又可分为一元及多元回归分析。
一、复习
3.对两个具有线性相关关系的变量进行回归分析的步骤:
1).画散点图;
2).求回归直线方程
3).用回归直线方程进行预报.
问题:对于线性相关的两个变量用什么方法来刻划之间的关系呢?
最小二乘法估计
最小二乘法估计下的线性回归方程:
探索:水稻产量y与施肥量x之间大致有何规律?
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
10 20 30 40 50
500
450
400
350
300
·
·
·
·
·
·
·
x
y
施化肥量
水稻产量
散点图
10 20 30 40 50
500
450
400
350
300
·
·
·
·
·
·
·
发现:图中各点,大致分布在某条直线附近。
探索2:在这些点附近可画直线不止一条, 哪条直线最能代表x与y之间的关系呢?
x
y
施化肥量
水稻产量
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
散点图
在Y与X的散点图上画出直线的方法很多。找出一条能够最好地描述Y与X(代表所有点)之间的直线。
最小二乘法的思路
问题是:怎样算“最好”?
最好指的是找一条直线使得所有这些点到该直线的纵向距离的和(平方和)最小。
10 20 30 40 50
500
450
400
350
300
·
·
·
·
·
·
·
x
y
施化肥量
水稻产量
求回归方程的方法:
用最小二乘法,其截距和斜率的估计公式为
例题1 从某大学中随机选出8名女大学生,其身高和体重数据如下表:
编号 1 2 3 4 5 6 7 8
身高 165 165 157 170 175 165 155 170
体重 48 57 50 54 64 61 43 59
求根据一名女大学生的身高预报她的体重的回归方程,并预报一名身高为172cm的女大学生的体重。
1.画散点图
身高
体重
2、由散点图知道身高和体重有比较好的线性相关关系,因此可以用线性回归方程刻画它们之间的关系。
3.求出截距和斜率:
1.画散点图
身高
体重
4.得出回归方程:
5.预报身高172女生体重:
探究P4:
身高为172cm的女大学生的体重一定是60.316kg吗?如果不是,你能解析一下原因吗?
(2)从散点图还可以看到,样本点散布在某一条直线的附近,而不是一条直线上,所以不能用一次函数y=bx+a来描述它们之间的关系。这时我们用下面的线性回归模型来描述身高和体重的关系:y=bx+a+e其中a和b为模型的未知参数,e是y与 之间的误差,通常e称为随机误差。
思考P4
产生随机误差项e的原因是什么?
随机误差e的来源(可以推广到一般):
1、其它因素的影响:影响身高 y 的因素不只是体重 x,可能 还包括遗传基因、饮食习惯、生长环境等因素;
2、用线性回归模型近似真实模型所引起的误差;
3、身高 y 的观测误差。
函数模型与回归模型之间的差别
函数模型:
回归模型:
可以提供
选择模型的准则
函数模型与回归模型之间的差别
函数模型:
回归模型:
线性回归模型y=bx+a+e增加了随机误差项e,因变量y的值由自变量x和随机误差项e共同确定,
即自变量x只能解释部分y的变化。
在统计中,我们也把自变量x称为解释变量,因变量y称为预报变量。
假设身高和随机误差的不同不会对体重产生任何影响,那么所有人的体重将相同。
在体重不受任何变量影响的假设下,设8名女大学生的体重都是她们的平均值,即8个人的体重都为54.5kg。
54.5
54.5
54.5
54.5
54.5
54.5
54.5
54.5
体重/kg
170
155
165
175
170
157
165
165
身高/cm
8
7
6
5
4
3
2
1
编号
编号 1 2 3 4 5 6 7 8
身高 165 165 157 170 175 165 155 170
体重 48 57 50 54 64 61 43 59
54.5kg
在散点图中,所有的点应该落在同一条水平直线上,但是观测到的数据并非如此。
这就意味着预报变量(体重)的值受解释变量(身高)或随机误差的影响。
编号 1 2 3 4 5 6 7 8
身高 165 165 157 170 175 165 155 170
体重 48 57 50 54 64 61 43 59
59
43
61
64
54
50
57
48
体重/kg
170
155
165
175
170
157
165
165
身高/cm
8
7
6
5
4
3
2
1
编号
例如,编号为6的女大学生的体重并没有落在水平直线上,她的体重为61kg。解析变量(身高)和随机误差共同把这名学生的体重从54.5kg“推”到了61kg,相差6.5kg,所以6.5kg是解释变量和随机误差的组合效应。
用这种方法可以对所有预报变量计算组合效应。
数学上,把每个效应(观测值减去总的平均值)的平方加起来,
即用 表示总的效应,称为总偏差平方和。
在例1中,总偏差平方和为354。
59
43
61
64
54
50
57
48
体重/kg
170
155
165
175
170
157
165
165
身高/cm
8
7
6
5
4
3
2
1
编号
那么,在这个总的效应(总偏差平方和)中,有多少来自于解析变量(身高)?有多少来自于随机误差?
假设随机误差对体重没有影响,也就是说,体重仅受身高的影响,那么散点图中所有的点将完全落在回归直线上。但是,在图中,数据点并没有完全落在回归
直线上。
这些点散布在回归直线附近,所以一定是随机误差把这些点从回归直线上“推”开了。
因此,数据点和它在回归直线上相应位置的差异 是随机误差的效应,称 为残差。
59
43
61
64
54
50
57
48
体重/kg
170
155
165
175
170
157
165
165
身高/cm
8
7
6
5
4
3
2
1
编号
在例1中,残差平方和约为128.361。
例如编号为6的女大学生计算随机误差的效应(残差)为:
对每名女大学生计算这个差异,然后分别将所得的值平方后加起来,用数学符号表示为:
称为残差平方和,它代表了随机误差的效应。
因此,数据点和它在回归直线上相应位置的差异 是随机误差的效应,称 为残差。
由于解释变量和随机误差的总效应(总偏差平方和)为354,而随机误差的效应为128.361,所以解释变量的效应为
解释变量和随机误差的总效应(总偏差平方和)
=解释变量的效应(回归平方和)
+随机误差的效应(残差平方和)
354-128.361=225.639
这个值称为回归平方和。
离差平方和的分解
(三个平方和的意义)
总偏差平方和(SST)
反映因变量的 n 个观察值与其均值的总离差
回归平方和(SSR)
反映自变量 x 的变化对因变量 y 取值变化的影响,或者说,是由于 x 与 y 之间的线性关系引起的 y 的取值变化,也称为可解释的平方和
残差平方和(SSE)
反映除 x 以外的其他因素对 y 取值的影响,也称为不可解释的平方和或剩余平方和
我们可以用相关指数R2来刻画回归的效果,其计算公式是
我们可以用相关指数R2来刻画回归的效果,其计算公式是
显然,R2的值越大,说明残差平方和越小,也就是说模型拟合效果越好。
在线性回归模型中,R2表示解释变量对预报变量变化的贡献率。
R2越接近1,表示回归的效果越好(因为R2越接近1,表示解释变量和预报变量的线性相关性越强)。
我们可以用相关指数R2来刻画回归的效果,其计算公式是
如果某组数据可能采取几种不同回归方程进行回归分析,则可以通过比较R2的值来做出选择,即选取R2较大的模型作为这组数据的模型。
总的来说:
相关指数R2是度量模型拟合效果的一种指标。
在线性模型中,它代表自变量刻画预报变量的能力。
1
354
总计
0.36
128.361
残差变量
0.64
225.639
解释变量
比例
平方和
来源
表1-3
从表1-3中可以看出,解释变量对总效应约贡献了64%,即R2 0.64,
可以叙述为“身高解析了64%的体重变化”,而随机误差贡献了剩余的36%。
所以,身高对体重的效应比随机误差的效应大得多。
下表列出了女大学生身高和体重的原始数据以及相应的残差数据。
残差分析与残差图的定义:
我们可以通过残差 来判断模型拟合的效果,判断原始数据中是否存在可疑数据,这方面的分析工作称为残差分析。
编号 1 2 3 4 5 6 7 8
身高/cm 165 165 157 170 175 165 155 170
体重/kg 48 57 50 54 64 61 43 59
残差 -6.373 2.627 2.419 -4.618 1.137 6.627 -2.883 0.382
我们可以利用图形来分析残差特性,作图时纵坐标为残差,横坐标可以选为样本编号,或身高数据,或体重估计值等,这样作出的图形称为残差图。
残差图的制作及作用。
坐标纵轴为残差变量,横轴可以有不同的选择;
若模型选择的正确,残差图中的点应该分布在以横轴为心的带形区域;
对于远离横轴的点,要特别注意。
身高与体重残差图
异常点
错误数据
模型问题
几点说明:
第一个样本点和第6个样本点的残差比较大,需要确认在采集过程中是否有人为的错误。如果数据采集有错误,就予以纠正,然后再重新利用线性回归模型拟合数据;如果数据采集没有错误,则需要寻找其他的原因。
另外,残差点比较均匀地落在水平的带状区域中,说明选用的模型计较合适,这样的带状区域的宽度越窄,说明模型拟合精度越高,回归方程的预报精度越高。
1)确定解释变量和预报变量;
2)画出散点图;
3)确定回归方程类型;
4)求出回归方程;
5)利用相关指数或残差进行分析.
建立回归模型的基本步骤
例2:一只红铃虫的产卵数y与温度x有关,现收集了7组观测数据,试建立y与x之间的回归方程
解:1)作散点图;
从散点图中可以看出产卵数和温度之间的关系并不能用线性回归模型来很好地近似。这些散点更像是集中在一条指数曲线或二次曲线的附近。
解: 令
则z=bx+a,(a=lnc1,b=c2),列出变换后数据表并画 出x与z 的散点图
x和z之间的关系可以用线性回归模型来拟合
x 21 23 25 27 29 32 35
z 1.946 2.398 3.045 3.178 4.19 4.745 5.784
2) 用 y=c3x2+c4 模型,令 ,则y=c3t+c4 ,列出变换后数据表并画出t与y 的散点图
散点并不集中在一条直线的附近,因此用线性回归模型拟合他们的效果不是最好的。
t 441 529 625 729 841 1024 1225
y 7 11 21 24 66 115 325
残 差 表
编号 1 2 3 4 5 6 7
x 21 23 25 27 29 32 35
y 7 11 21 24 66 115 325
e(1) 0.52 -0.167 1.76 -9.149 8.889 -14.153 32.928
e(2) 47.7 19.397 -5.835 -41.003 -40.107 -58.268 77.965
非线性回归方程
二次回归方程
残差公式
方法:把非线性的回归问题化为线性问题来考虑,
通过变换来实现。
(1)根据数据,作散点图 ;
(2)由经验确定回归方程的类型(如观察到数据呈
线性关系,则选用线性回归方程y=bx+a) ;
(3)若呈指数关系,则设为
