人教版初中三年级相似多边形的性质
文档属性
| 名称 | 人教版初中三年级相似多边形的性质 |  | |
| 格式 | zip | ||
| 文件大小 | 135.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-10 23:05:08 | ||
图片预览

文档简介
(共13张PPT)
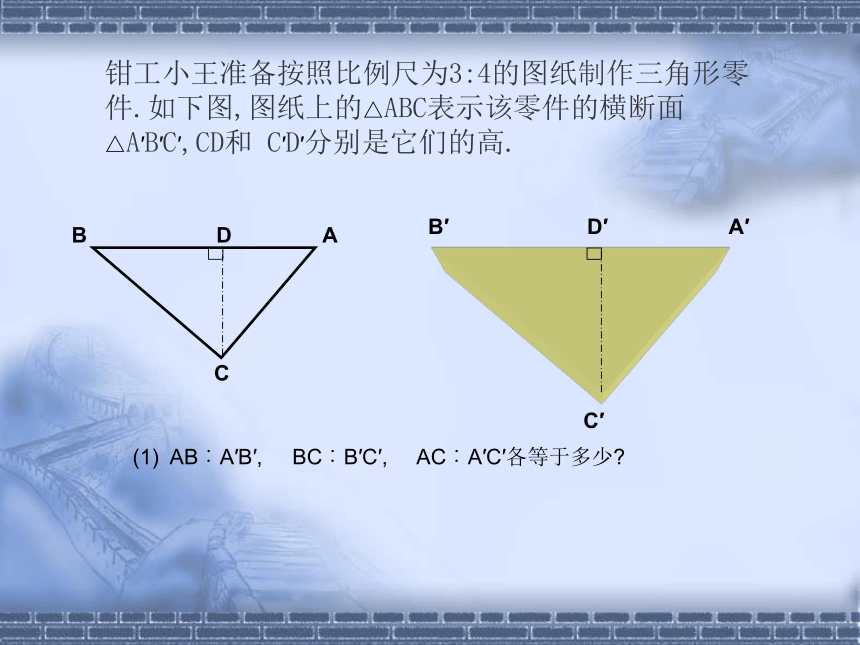
钳工小王准备按照比例尺为3:4的图纸制作三角形零件.如下图,图纸上的△ABC表示该零件的横断面△A′B′C′,CD和 C′D′分别是它们的高.
(1) AB︰A′B′, BC︰B′C′, AC︰A′C′各等于多少
B
A
C
D
B′
A′
C′
D′
B
A
C
D
B′
A′
C′
D′
0
1
2
3
4
5
6
8
9
10
7
BC
B′
C′
=
4
3
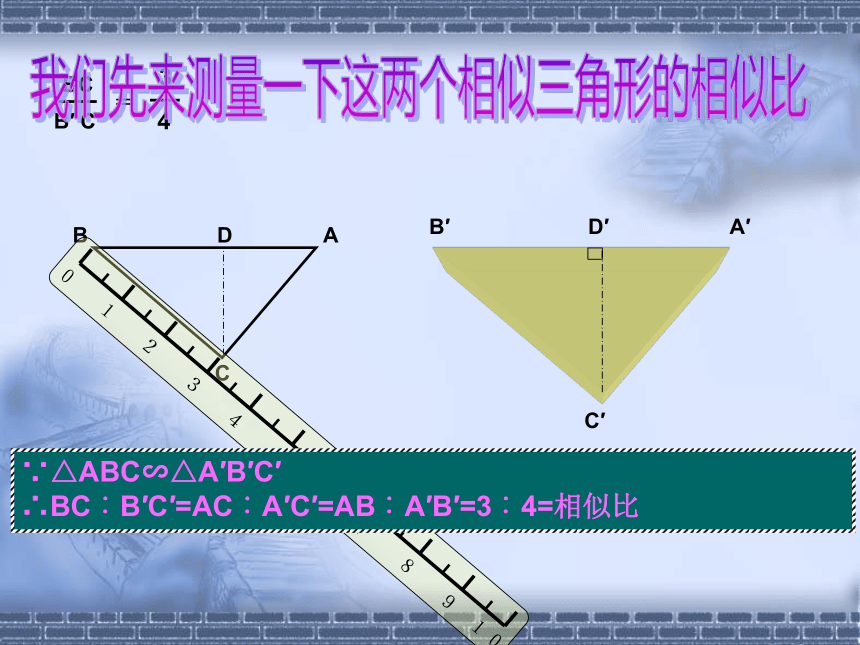
∵△ABC∽△A′B′C′
∴BC︰B′C′=AC︰A′C′=AB︰A′B′=3︰4=相似比
B
A
C
D
B′
A′
C′
D′
0
1
2
3
4
5
6
8
9
10
7
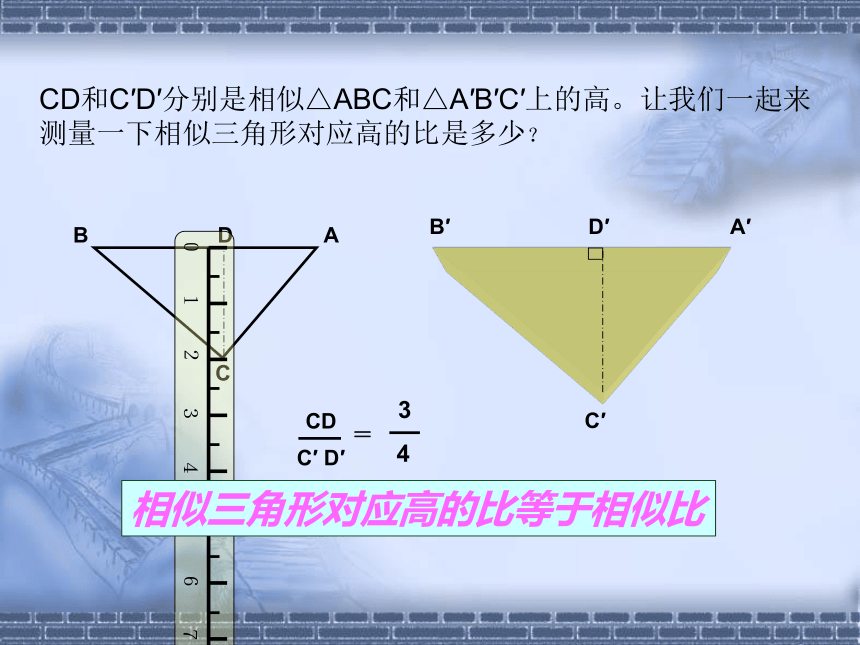
CD和C′D′分别是相似△ABC和△A′B′C′上的高。让我们一起来测量一下相似三角形对应高的比是多少?
CD
C′
D′
=
4
3
相似三角形对应高的比等于相似比
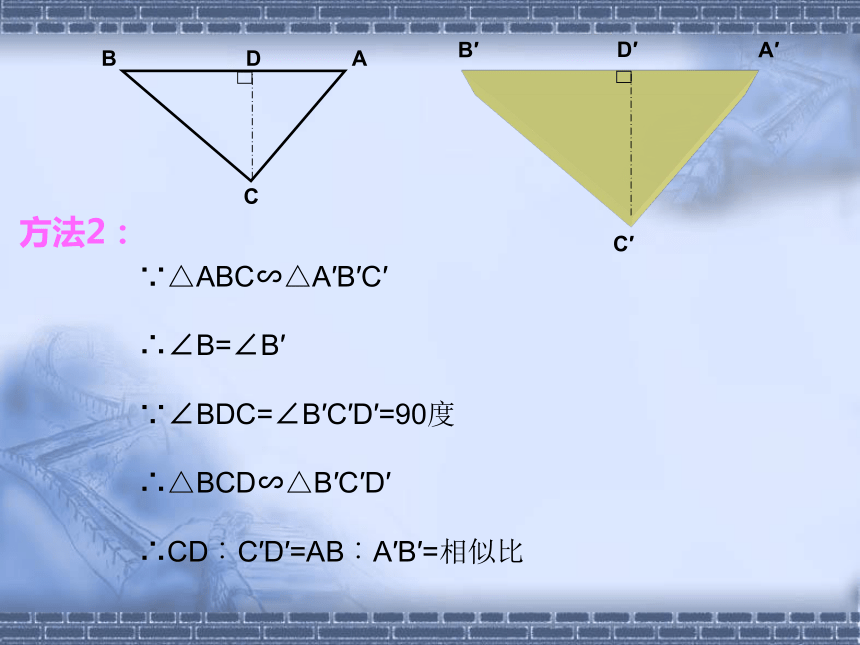
∵△ABC∽△A′B′C′
∴∠B=∠B′
∵∠BDC=∠B′C′D′=90度
∴△BCD∽△B′C′D′
∴CD︰C′D′=AB︰A′B′=相似比
方法2:
B
A
C
D
B′
A′
C′
D′
AE
A′
E′
=
4
3
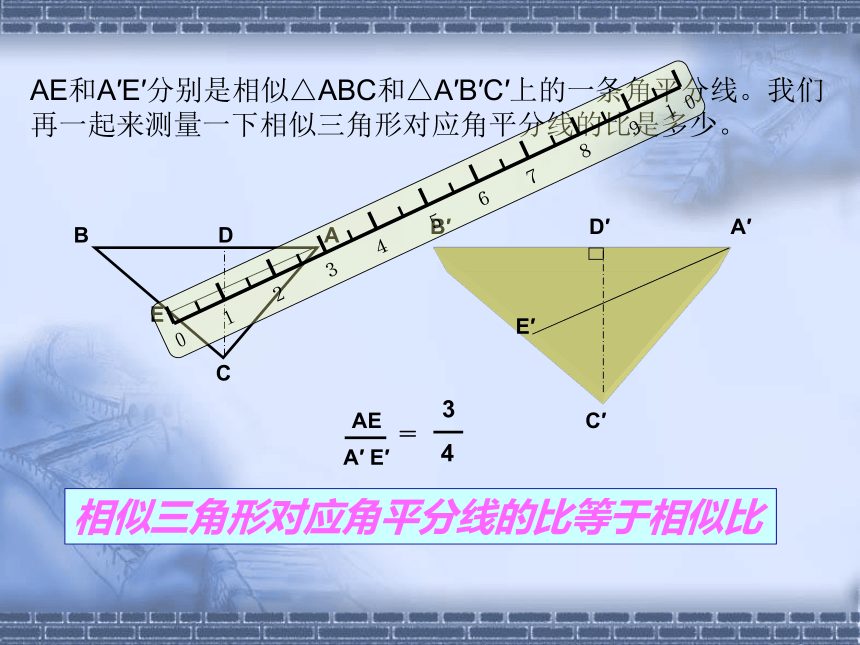
AE和A′E′分别是相似△ABC和△A′B′C′上的一条角平分线。我们再一起来测量一下相似三角形对应角平分线的比是多少。
相似三角形对应角平分线的比等于相似比
B
A
C
D
B′
A′
C′
D′
E′
E
0
1
2
3
4
5
6
8
9
10
7
方法2:
∵△ABC∽△A′B′C′
∴∠B=∠B′
∠BAC=∠B′A′C′
又∵AE, A′E′分别平分
∠BAC=∠B′A′C′
∴∠BAE=∠B′A′E′
∴△ABE∽△A′B′E′
∴AE︰A′E′=AB︰A′B′=相似比
B
A
C
D
B′
A′
C′
D′
E′
E
B
A
C
D
B′
A′
C′
D′
F
F′
CE和C′E′分别是相似△ABC和△A′B′C′的AB和A′B′边上的中线。我们再一起来测量一下相似三角形对应中线的比是多少?
C F
C′F′
=
4
3
相似三角形的对应中线的比等于相似比
0
1
2
3
4
5
6
8
9
10
7
对应高的比
对应角平分线的比
对应中线的比
等于相似比
如图,AD是△ABC的高,点P、Q在BC边上,点R在AC边 上,点S在AB边上,BC=60cm,AD=40cm,四边形PQRS是正方形.
△ASR与△ABC相似吗 为什么
求正方形PQRS的边长
A
B
C
D
E
S
R
P
Q
解(1)△ABC∽△ASR。理由是:
∵PQRS是正方形
∴SR∥BC
∴∠ASR=∠ABC
∠ARS=∠ACB
∴△ASR∽△ABC
(两角对应相等的两个三角形相似)
(2)∵△ASR∽△ABC。
根据相似三角形对应高的比等于相似比
∴AE︰AD=SR︰BC
设正方形PQRS的边长 cm,
则AE=(40 – X)cm.所以
40 - X ︰40= X︰60
∴ X =24
∴正方形PQRS的边长为24cm。
A
B
C
D
E
S
R
P
Q
练习题:
1.我校计划在一块三角形空地上修建一个面积最大的正方形水池,使得水池的一边在△ABC的边BC上,已知BC=60cm,高AD=30cm,则该水池的边长为( )
A. 10cm B. 20cm C. 30cm D. 40cm
2 .AD 、A′D′分别是△ABC和△ABC的角平分线,且
AB︰A′B′= BD︰B′D′=AD︰A′D′
求证: △ABC ∽△A′B′C′
钳工小王准备按照比例尺为3:4的图纸制作三角形零件.如下图,图纸上的△ABC表示该零件的横断面△A′B′C′,CD和 C′D′分别是它们的高.
(1) AB︰A′B′, BC︰B′C′, AC︰A′C′各等于多少
B
A
C
D
B′
A′
C′
D′
B
A
C
D
B′
A′
C′
D′
0
1
2
3
4
5
6
8
9
10
7
BC
B′
C′
=
4
3
∵△ABC∽△A′B′C′
∴BC︰B′C′=AC︰A′C′=AB︰A′B′=3︰4=相似比
B
A
C
D
B′
A′
C′
D′
0
1
2
3
4
5
6
8
9
10
7
CD和C′D′分别是相似△ABC和△A′B′C′上的高。让我们一起来测量一下相似三角形对应高的比是多少?
CD
C′
D′
=
4
3
相似三角形对应高的比等于相似比
∵△ABC∽△A′B′C′
∴∠B=∠B′
∵∠BDC=∠B′C′D′=90度
∴△BCD∽△B′C′D′
∴CD︰C′D′=AB︰A′B′=相似比
方法2:
B
A
C
D
B′
A′
C′
D′
AE
A′
E′
=
4
3
AE和A′E′分别是相似△ABC和△A′B′C′上的一条角平分线。我们再一起来测量一下相似三角形对应角平分线的比是多少。
相似三角形对应角平分线的比等于相似比
B
A
C
D
B′
A′
C′
D′
E′
E
0
1
2
3
4
5
6
8
9
10
7
方法2:
∵△ABC∽△A′B′C′
∴∠B=∠B′
∠BAC=∠B′A′C′
又∵AE, A′E′分别平分
∠BAC=∠B′A′C′
∴∠BAE=∠B′A′E′
∴△ABE∽△A′B′E′
∴AE︰A′E′=AB︰A′B′=相似比
B
A
C
D
B′
A′
C′
D′
E′
E
B
A
C
D
B′
A′
C′
D′
F
F′
CE和C′E′分别是相似△ABC和△A′B′C′的AB和A′B′边上的中线。我们再一起来测量一下相似三角形对应中线的比是多少?
C F
C′F′
=
4
3
相似三角形的对应中线的比等于相似比
0
1
2
3
4
5
6
8
9
10
7
对应高的比
对应角平分线的比
对应中线的比
等于相似比
如图,AD是△ABC的高,点P、Q在BC边上,点R在AC边 上,点S在AB边上,BC=60cm,AD=40cm,四边形PQRS是正方形.
△ASR与△ABC相似吗 为什么
求正方形PQRS的边长
A
B
C
D
E
S
R
P
Q
解(1)△ABC∽△ASR。理由是:
∵PQRS是正方形
∴SR∥BC
∴∠ASR=∠ABC
∠ARS=∠ACB
∴△ASR∽△ABC
(两角对应相等的两个三角形相似)
(2)∵△ASR∽△ABC。
根据相似三角形对应高的比等于相似比
∴AE︰AD=SR︰BC
设正方形PQRS的边长 cm,
则AE=(40 – X)cm.所以
40 - X ︰40= X︰60
∴ X =24
∴正方形PQRS的边长为24cm。
A
B
C
D
E
S
R
P
Q
练习题:
1.我校计划在一块三角形空地上修建一个面积最大的正方形水池,使得水池的一边在△ABC的边BC上,已知BC=60cm,高AD=30cm,则该水池的边长为( )
A. 10cm B. 20cm C. 30cm D. 40cm
2 .AD 、A′D′分别是△ABC和△ABC的角平分线,且
AB︰A′B′= BD︰B′D′=AD︰A′D′
求证: △ABC ∽△A′B′C′
