8.5 空间直线、平面的平行(2)课件(共19张PPT)
文档属性
| 名称 | 8.5 空间直线、平面的平行(2)课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-05 00:00:00 | ||
图片预览






文档简介
第8章 立体几何初步
8.5 空间直线、
平面的平行(2)
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
高中数学人教A版(2019)必修第二册
三种平行关系
空间中的平行关系是一种重要的特殊关系,一般以证明题的形式出现,总结如下:
基本事实④(平行线的传递性):????//????,????//?????????//????
?
线线平行的定义:在同一平面内,永不相交的两条直线叫做平行线
平面几何知识:证明共面的两条直线平行.主要有三角形中位线定理;平行四边形的性质;平行线分线段成比例定理;梯形一组对边平行;同位角相等或同旁内角互补两直线平行;向量共线等等
【1】直线与直线平行的判定方法
探究新知
三种平行关系
空间中的平行关系是一种重要的特殊关系,一般以证明题的形式出现,总结如下:
面面平行的性质定理:????//????,????∩????=????,????∩????=????,????//????
?
线面平行的性质定理:????//????,?????????,????∩????=????,????//????
?
线面垂直的性质定理:????⊥????,????⊥?????????//????
?
反证法
【1】直线与直线平行的判定方法
三种平行关系
空间中的平行关系是一种重要的特殊关系,一般以证明题的形式出现,总结如下:
线面平行的判定定理:?????????,?????????,????//?????????//????
?
线面平行的定义:直线与平面没有公共点
面面平行的性质:????//????,??????????????//????
?
【2】直线与平面平行的判定方法
反证法
三种平行关系
空间中的平行关系是一种重要的特殊关系,一般以证明题的形式出现,总结如下:
面面平行的判定定理:a//α,b//α,a∩b=P,a?β,b?β?α//β
?
面面平行的定义:两个平面没有公共点
面面平行的判定定理的推论:a?β,b?β,a∩b=P,a′?α,b′?α, a′∩b′=P′,a//a′,b//b′ ?α//β
?
【3】平面与平面平行的判定方法
面面平行的传递性:a//γ,β//γ?α//β
?
反证法
三种平行关系
空间中的平行关系是一种重要的特殊关系,一般以证明题的形式出现,总结如下:
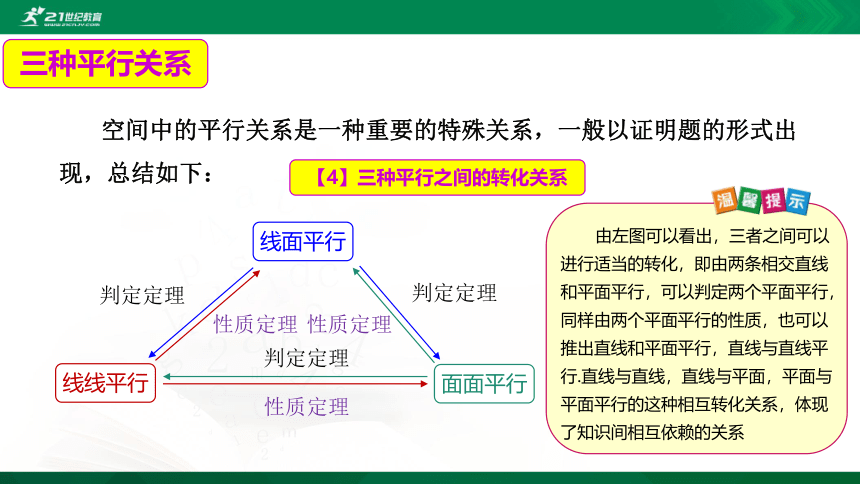
【4】三种平行之间的转化关系
线面平行
线线平行
面面平行
判定定理
判定定理
性质定理
性质定理
判定定理
性质定理
由左图可以看出,三者之间可以进行适当的转化,即由两条相交直线和平面平行,可以判定两个平面平行,同样由两个平面平行的性质,也可以推出直线和平面平行,直线与直线平行.直线与直线,直线与平面,平面与平面平行的这种相互转化关系,体现了知识间相互依赖的关系
正方形ABCD与正方形ABEF所在平面相交于AB,在AE,BD上各有一点P,Q.且AP=DQ,求证:PQ//平面BCE.
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
如图,在平面????????????????内,过点????作????????//????????,交????????于点????,连接????????,∴ ?????????//平面????????????
?
????
?
∵ ?????????//????????,∴????????????????=????????????????.又∵????????=????????,????????=????????,∴????????=????????
?
∴????????????????=????????????????,∴????????????????=????????????????.即????????//????????.又????????//?????????,∴ ????????//????????
?
∵ ?????????平面????????????,?????????平面????????????,∴????????//平面????????????,又????????∩????????=????,
?
∴平面????????????//平面????????????.又?????????平面????????????, ∴?????????//平面????????????
?
例题讲解
判定定理条件罗列不全而出错
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PA=AD=1,E,F分别是AB和PD的中点.求证:直线AF//平面PEC.
如图,过点????作????????//????????, 交????????于点????,连接????????.
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
∵点????为????????的中点,∴????????=????????????????.
?
∵点????为????????的中点,∴????????=????????????????=????????.
?
又∵点????????//????????, ∴四边形????????????????为平行四边形.
?
∴ ????????//????????. ∵ ?????????平面????????????,?????????平面????????????
?
∴ 直线????????//平面????????????
?
证明平行四边形时忘记四点共面
如图,已知????,????分别是正方体?????????????????????????????????????????????????的棱????????1,????????????的中点,求证:四边形????????????1????是平行四边形.
?
∵ 平面????????????1????1//平面????????????1????1,
平面????????????1????1?∩ 平面????????????1????=????????,
平面????????????1????1?∩平面????????????1????=????1????,
∴ ?????????//????1????,同理得????????1//????????,
∴四边形????????????1????为平行四边形
?
????
?
????
?
????
?
????
?
????
?
????
?
????????
?
????????
?
????????
?
????????
?
空间三点一定共面,四点不一定共面.题中没有说B,E,D1, F四点共面,如果要用,则需要证明
?
证明平行四边形时忘记四点共面
如图,已知????,????分别是正方体?????????????????????????????????????????????????的棱????????1,????????????的中点,求证:四边形????????????1????是平行四边形.
?
证明:如图,取????????1的中点????,连接????????,????????
?
????
?
????
?
????
?
????
?
????
?
????
?
????????
?
????????
?
????????
?
????????
?
????
?
∵ ????是????????1的中点, ????是????????1的中点,
?
∴ ????????//????????,????????=????????.由正方体的性质知
?
????????//????????,????????=????????,?∴ ????????//????????,????????=????????,
?
∴ 四边形????????????????是平行四边形,∴ ????????//????????,??????=?????????①
?
又∵????,????分别是????????1?和????????1?的中点,∴????1????//????????,????1????=????????
?
∴ 四边形????1????????????是平行四边形,∴????1????//????????,????1????=???????? ②
?
由①②得????1????//????????, ????1????=????????,?∴四边形????????????1????是平行四边形
?
如图,已知在棱长为????的正方体?????????????????????????????????????????????????中, ????,????分别是棱????????,????????的中点,求证:四边形????????????1????1是梯形.
?
题①
——平面基本事实④和等角定理的应用
????????
?
????????
?
????????
?
????????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
如图,连接????????,在Δ????????????中,∵ ????,????分别是棱????????,????????的中点,∴ ????????是Δ????????????的中位线.
?
∴ ????????//????????,????????=12????????. 由正方体的性质得????????//????1????1 ,????????=????1????1
?
∴ ????????//????1????1?,且????????=12????1????1?,∴ ????????≠????1????1
?
易知????????1与????????1不平行,∴四边形????????????1????1是梯形
?
如图,在直三棱柱?????????????????????????????????????中, ????是????????的中点,求证:????????1 //平面????1????????.
?
题②
——直线与平面平行的判定
如图,连接????????1交????1?????于点????,连接????????.
?
∴ 四边形????????1????1????为矩形,∴ 点????是????????1的中点
?
又∵ 在Δ????????????1中,????是????????的中点,∴ ????????1 //????????
?
∵ ?????????平面????1????????,????????1?平面????1????????
?
????
?
????
?
????
?
????
?
????????
?
????????
?
????????
?
∴ ????????1 //平面????1????????
?
????
?
下列说法正确的是( )
A. 若????,????是两条直线,且????//????,则????平行于经过????的任何平面
B. 若直线????和平面????满足????//????,则????与????内的任一直线都平行
C. 若????,????直线和平面????满足?????//????, ?????// ?????,则????//????
D.若????,????直线和平面????满足?????//????, ?????// ?????,?????????,则????//????
?
题③
——直线与平面平行的性质
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
如图,在正方体?????????????????????1????1????1????1中,????,????,????,????分别是
????1????1,????1????1,????1????1,????1????1的中点,求证:????,????, ????,????四点共面.
?
题④
——平面与平面平行的判定
????????
?
????????
?
????????
?
????????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
如图,连接????1????1
?
∵ ????,????分别是????1????1,????1????1的中点,
?
∴ ????????//????1????1
?
由正方体的性质可知∴????????//????1????1
?
∴ ????????//????????,即????,????, ????,????四点共面.
?
????
?
如图,????????,????????是夹在两个平行平面????,????之间的线段,????,????分别是????????,????????的中点,求证: ?????????//????.
?
题⑤
——平面与平面平行的性质
????
?
????
?
????
?
????
?
若????????,????????在同一平面内,则平面????????????????与的????,????交线分别为????????, ????????.
?
????
?
????
?
∵?????//????,∴ ?????????// ????????
?
∵ ????,????分别是????????,????????的中点,∴ ?????????// ????????
?
又∵?????????????,?????????????, ∴ ?????????//????
?
如图,????????,????????是夹在两个平行平面????,????之间的线段,????,????分别是????????,????????的中点,求证: ?????????//????.
?
题⑤
——平面与平面平行的性质
????
?
????
?
????
?
????
?
????
?
????
?
若????????,????????异面,如图,过点????作????????//????????交????于点????,取????????的中点????,连接????????,????????,????????,????????. ∵????????//?????????,∴????????,????????确定平面????????????????,且与的????,????交线分别为????????,????????.
?
????
?
????
?
????
?
????
?
∵????//????,∴????????//????????,?又∵????,????分别是????????,????????的中点,∴ ????????//????????
?
∵?????????????,?????????????, ∴?????????//????,同理可证?????????//????
?
∵????????∩????????=????, ????????,?????????平面????????????,∴平面?????????????//????
?
又∵?????????平面????????????,∴ ?????????//????
?
如图所示,在正方体?????????????????????1????1????1????1中,????为底面的中心,????是????????1的中点,????是????????1上的动点.问:当????点在什么位置时,平面????1?????????//平面?????????????
?
题⑥
——线面平行、面面平行的探索性问题
当????为????????1的中点时,平面????1?????????//平面????????????.
?
????
?
????
?
????
?
????
?
????
?
????????
?
????????
?
????????
?
????????
?
????
?
????
?
如图,连接????????,????????,则????为????????的中点.
?
∵ ????为????????1的中点, ????是????????1的中点,∴????????//????????,????????=????????
?
又∵????????//????????,????????=????????,∴ ????????//????????,????????=????????,
?
∴四边形????????????????为平行四边形,∴????????//????????
?
又∵?????????平面????????????,?????????平面????????????,∴ ????????//平面????????????
?
∵????为????????的中点, ????是????????1的中点,∴????????//????1????,又∵ ?????????平面????????????,????1?????平面????????????
?
∴ ????1?????//平面????????????.∵ ????1????,?????????平面????1????????,????1????∩????????=????
?
∴平面????1?????????//平面????????????
?
谢谢聆听
8.5 空间直线、
平面的平行(2)
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
高中数学人教A版(2019)必修第二册
三种平行关系
空间中的平行关系是一种重要的特殊关系,一般以证明题的形式出现,总结如下:
基本事实④(平行线的传递性):????//????,????//?????????//????
?
线线平行的定义:在同一平面内,永不相交的两条直线叫做平行线
平面几何知识:证明共面的两条直线平行.主要有三角形中位线定理;平行四边形的性质;平行线分线段成比例定理;梯形一组对边平行;同位角相等或同旁内角互补两直线平行;向量共线等等
【1】直线与直线平行的判定方法
探究新知
三种平行关系
空间中的平行关系是一种重要的特殊关系,一般以证明题的形式出现,总结如下:
面面平行的性质定理:????//????,????∩????=????,????∩????=????,????//????
?
线面平行的性质定理:????//????,?????????,????∩????=????,????//????
?
线面垂直的性质定理:????⊥????,????⊥?????????//????
?
反证法
【1】直线与直线平行的判定方法
三种平行关系
空间中的平行关系是一种重要的特殊关系,一般以证明题的形式出现,总结如下:
线面平行的判定定理:?????????,?????????,????//?????????//????
?
线面平行的定义:直线与平面没有公共点
面面平行的性质:????//????,??????????????//????
?
【2】直线与平面平行的判定方法
反证法
三种平行关系
空间中的平行关系是一种重要的特殊关系,一般以证明题的形式出现,总结如下:
面面平行的判定定理:a//α,b//α,a∩b=P,a?β,b?β?α//β
?
面面平行的定义:两个平面没有公共点
面面平行的判定定理的推论:a?β,b?β,a∩b=P,a′?α,b′?α, a′∩b′=P′,a//a′,b//b′ ?α//β
?
【3】平面与平面平行的判定方法
面面平行的传递性:a//γ,β//γ?α//β
?
反证法
三种平行关系
空间中的平行关系是一种重要的特殊关系,一般以证明题的形式出现,总结如下:
【4】三种平行之间的转化关系
线面平行
线线平行
面面平行
判定定理
判定定理
性质定理
性质定理
判定定理
性质定理
由左图可以看出,三者之间可以进行适当的转化,即由两条相交直线和平面平行,可以判定两个平面平行,同样由两个平面平行的性质,也可以推出直线和平面平行,直线与直线平行.直线与直线,直线与平面,平面与平面平行的这种相互转化关系,体现了知识间相互依赖的关系
正方形ABCD与正方形ABEF所在平面相交于AB,在AE,BD上各有一点P,Q.且AP=DQ,求证:PQ//平面BCE.
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
如图,在平面????????????????内,过点????作????????//????????,交????????于点????,连接????????,∴ ?????????//平面????????????
?
????
?
∵ ?????????//????????,∴????????????????=????????????????.又∵????????=????????,????????=????????,∴????????=????????
?
∴????????????????=????????????????,∴????????????????=????????????????.即????????//????????.又????????//?????????,∴ ????????//????????
?
∵ ?????????平面????????????,?????????平面????????????,∴????????//平面????????????,又????????∩????????=????,
?
∴平面????????????//平面????????????.又?????????平面????????????, ∴?????????//平面????????????
?
例题讲解
判定定理条件罗列不全而出错
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PA=AD=1,E,F分别是AB和PD的中点.求证:直线AF//平面PEC.
如图,过点????作????????//????????, 交????????于点????,连接????????.
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
∵点????为????????的中点,∴????????=????????????????.
?
∵点????为????????的中点,∴????????=????????????????=????????.
?
又∵点????????//????????, ∴四边形????????????????为平行四边形.
?
∴ ????????//????????. ∵ ?????????平面????????????,?????????平面????????????
?
∴ 直线????????//平面????????????
?
证明平行四边形时忘记四点共面
如图,已知????,????分别是正方体?????????????????????????????????????????????????的棱????????1,????????????的中点,求证:四边形????????????1????是平行四边形.
?
∵ 平面????????????1????1//平面????????????1????1,
平面????????????1????1?∩ 平面????????????1????=????????,
平面????????????1????1?∩平面????????????1????=????1????,
∴ ?????????//????1????,同理得????????1//????????,
∴四边形????????????1????为平行四边形
?
????
?
????
?
????
?
????
?
????
?
????
?
????????
?
????????
?
????????
?
????????
?
空间三点一定共面,四点不一定共面.题中没有说B,E,D1, F四点共面,如果要用,则需要证明
?
证明平行四边形时忘记四点共面
如图,已知????,????分别是正方体?????????????????????????????????????????????????的棱????????1,????????????的中点,求证:四边形????????????1????是平行四边形.
?
证明:如图,取????????1的中点????,连接????????,????????
?
????
?
????
?
????
?
????
?
????
?
????
?
????????
?
????????
?
????????
?
????????
?
????
?
∵ ????是????????1的中点, ????是????????1的中点,
?
∴ ????????//????????,????????=????????.由正方体的性质知
?
????????//????????,????????=????????,?∴ ????????//????????,????????=????????,
?
∴ 四边形????????????????是平行四边形,∴ ????????//????????,??????=?????????①
?
又∵????,????分别是????????1?和????????1?的中点,∴????1????//????????,????1????=????????
?
∴ 四边形????1????????????是平行四边形,∴????1????//????????,????1????=???????? ②
?
由①②得????1????//????????, ????1????=????????,?∴四边形????????????1????是平行四边形
?
如图,已知在棱长为????的正方体?????????????????????????????????????????????????中, ????,????分别是棱????????,????????的中点,求证:四边形????????????1????1是梯形.
?
题①
——平面基本事实④和等角定理的应用
????????
?
????????
?
????????
?
????????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
如图,连接????????,在Δ????????????中,∵ ????,????分别是棱????????,????????的中点,∴ ????????是Δ????????????的中位线.
?
∴ ????????//????????,????????=12????????. 由正方体的性质得????????//????1????1 ,????????=????1????1
?
∴ ????????//????1????1?,且????????=12????1????1?,∴ ????????≠????1????1
?
易知????????1与????????1不平行,∴四边形????????????1????1是梯形
?
如图,在直三棱柱?????????????????????????????????????中, ????是????????的中点,求证:????????1 //平面????1????????.
?
题②
——直线与平面平行的判定
如图,连接????????1交????1?????于点????,连接????????.
?
∴ 四边形????????1????1????为矩形,∴ 点????是????????1的中点
?
又∵ 在Δ????????????1中,????是????????的中点,∴ ????????1 //????????
?
∵ ?????????平面????1????????,????????1?平面????1????????
?
????
?
????
?
????
?
????
?
????????
?
????????
?
????????
?
∴ ????????1 //平面????1????????
?
????
?
下列说法正确的是( )
A. 若????,????是两条直线,且????//????,则????平行于经过????的任何平面
B. 若直线????和平面????满足????//????,则????与????内的任一直线都平行
C. 若????,????直线和平面????满足?????//????, ?????// ?????,则????//????
D.若????,????直线和平面????满足?????//????, ?????// ?????,?????????,则????//????
?
题③
——直线与平面平行的性质
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
如图,在正方体?????????????????????1????1????1????1中,????,????,????,????分别是
????1????1,????1????1,????1????1,????1????1的中点,求证:????,????, ????,????四点共面.
?
题④
——平面与平面平行的判定
????????
?
????????
?
????????
?
????????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
如图,连接????1????1
?
∵ ????,????分别是????1????1,????1????1的中点,
?
∴ ????????//????1????1
?
由正方体的性质可知∴????????//????1????1
?
∴ ????????//????????,即????,????, ????,????四点共面.
?
????
?
如图,????????,????????是夹在两个平行平面????,????之间的线段,????,????分别是????????,????????的中点,求证: ?????????//????.
?
题⑤
——平面与平面平行的性质
????
?
????
?
????
?
????
?
若????????,????????在同一平面内,则平面????????????????与的????,????交线分别为????????, ????????.
?
????
?
????
?
∵?????//????,∴ ?????????// ????????
?
∵ ????,????分别是????????,????????的中点,∴ ?????????// ????????
?
又∵?????????????,?????????????, ∴ ?????????//????
?
如图,????????,????????是夹在两个平行平面????,????之间的线段,????,????分别是????????,????????的中点,求证: ?????????//????.
?
题⑤
——平面与平面平行的性质
????
?
????
?
????
?
????
?
????
?
????
?
若????????,????????异面,如图,过点????作????????//????????交????于点????,取????????的中点????,连接????????,????????,????????,????????. ∵????????//?????????,∴????????,????????确定平面????????????????,且与的????,????交线分别为????????,????????.
?
????
?
????
?
????
?
????
?
∵????//????,∴????????//????????,?又∵????,????分别是????????,????????的中点,∴ ????????//????????
?
∵?????????????,?????????????, ∴?????????//????,同理可证?????????//????
?
∵????????∩????????=????, ????????,?????????平面????????????,∴平面?????????????//????
?
又∵?????????平面????????????,∴ ?????????//????
?
如图所示,在正方体?????????????????????1????1????1????1中,????为底面的中心,????是????????1的中点,????是????????1上的动点.问:当????点在什么位置时,平面????1?????????//平面?????????????
?
题⑥
——线面平行、面面平行的探索性问题
当????为????????1的中点时,平面????1?????????//平面????????????.
?
????
?
????
?
????
?
????
?
????
?
????????
?
????????
?
????????
?
????????
?
????
?
????
?
如图,连接????????,????????,则????为????????的中点.
?
∵ ????为????????1的中点, ????是????????1的中点,∴????????//????????,????????=????????
?
又∵????????//????????,????????=????????,∴ ????????//????????,????????=????????,
?
∴四边形????????????????为平行四边形,∴????????//????????
?
又∵?????????平面????????????,?????????平面????????????,∴ ????????//平面????????????
?
∵????为????????的中点, ????是????????1的中点,∴????????//????1????,又∵ ?????????平面????????????,????1?????平面????????????
?
∴ ????1?????//平面????????????.∵ ????1????,?????????平面????1????????,????1????∩????????=????
?
∴平面????1?????????//平面????????????
?
谢谢聆听
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
