8.4.1 平面-课件(共20张PPT)
文档属性
| 名称 | 8.4.1 平面-课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-06 15:28:10 | ||
图片预览




文档简介
第8章 立体几何初步
8.4.1 平 面
高中数学人教A版(2019)必修第二册
平面的概念与画法
【直观理解】课桌面、黑板面、教室平面、平静的水面都给我们以平面
的直观感觉,但它们都不是平面,而是平面的一部分.
【抽象理解】平面是平的,是无限延展的,没有厚薄,大小之分
平面的概念
平面与平面图形的区别和联系
平面是不可度量的;是无限延展,无厚薄,无大小的理想的面
我们日常接触到的是平面图形,如三角形,正方形,圆等,它们有大小之分,它们都不是平面,而是平面的一部分
我们可以用平面图形来表示平面
探究新知
平面的概念与画法
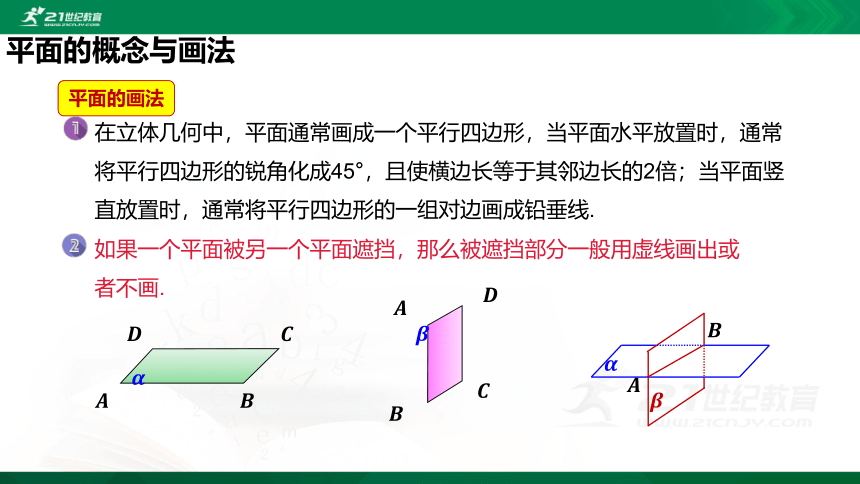
平面的画法
如果一个平面被另一个平面遮挡,那么被遮挡部分一般用虚线画出或者不画.
在立体几何中,平面通常画成一个平行四边形,当平面水平放置时,通常将平行四边形的锐角化成45°,且使横边长等于其邻边长的2倍;当平面竖直放置时,通常将平行四边形的一组对边画成铅垂线.
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
平面的概念与画法
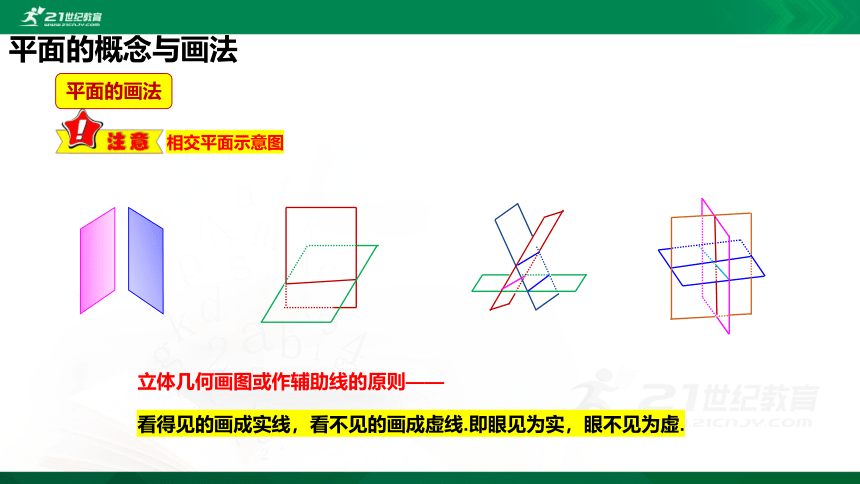
平面的画法
相交平面示意图
立体几何画图或作辅助线的原则——
看得见的画成实线,看不见的画成虚线.即眼见为实,眼不见为虚.
平面的概念与画法
平面的表示
通常用平行四边形来表示平面.有时候也会用其他图形来表示平面,如三角形,矩形,梯形,圆等等.
①常用希腊字母 ????,????,???? 等表示平面,如平面 ????、
平面 ????、平面 ???? 等等.
?
②用大写英文字母表示平面,如对角线字母表
示平面,比如平面AC,平面BD等等.
③用平行四边形的四个顶点字母来表示平面,
如平面ABCD
④用平面内不共线的三个点来表示平面,如平面PHQ
用希腊字母α,β,γ等表示平面时,若已知条件说明了平面α,平面β,则之后可以省略“平面”二字;用大写英文字母表示的时候则不能省略.
?
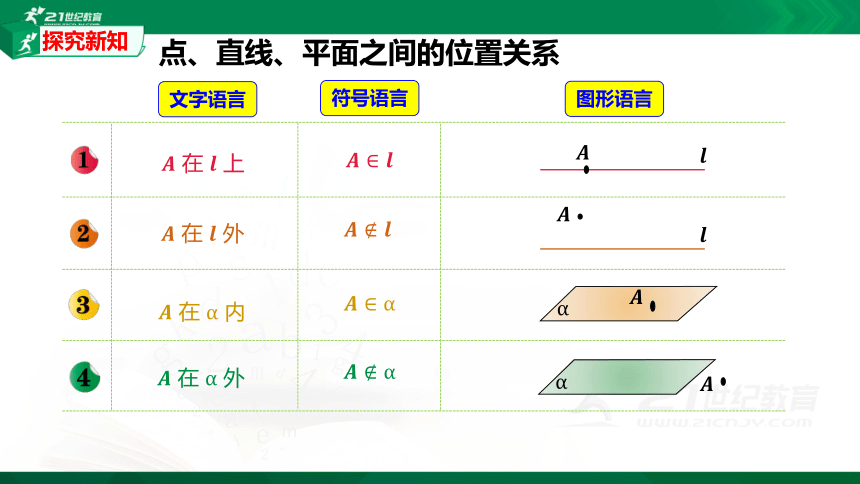
点、直线、平面之间的位置关系
???? 在 ???? 上
?
文字语言
符号语言
图形语言
???? 在 ???? 外
?
???? 在 α 内
?
???? 在 α 外
?
????∈????
?
????
?
????
?
?????????
?
????
?
????
?
α
?
????∈α
?
????
?
?????α
?
α
?
????
?
探究新知
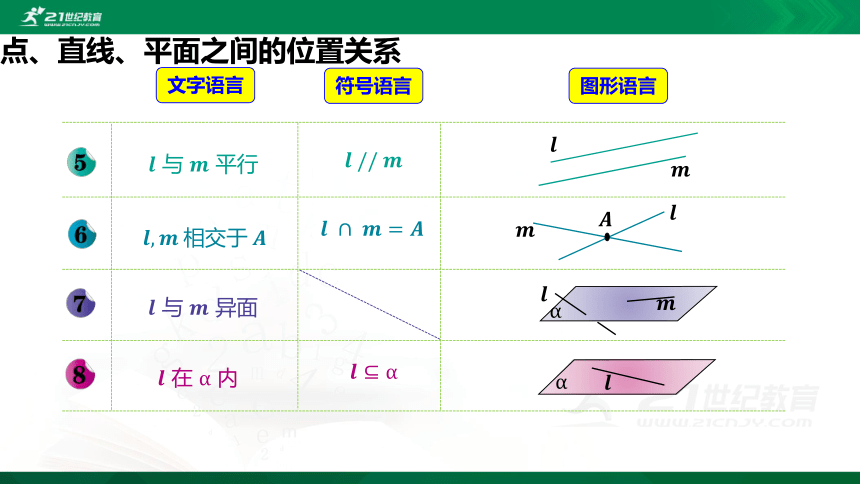
点、直线、平面之间的位置关系
???? 与 ???? 平行
?
文字语言
符号语言
图形语言
????,?????相交于?????
?
???? 与 ???? 异面
?
???? 在 α 内
?
?????//?????
?
????
?
????
?
?????∩?????=????
?
????
?
????
?
α
?
?????α
?
α
?
????
?
????
?
????
?
????
?
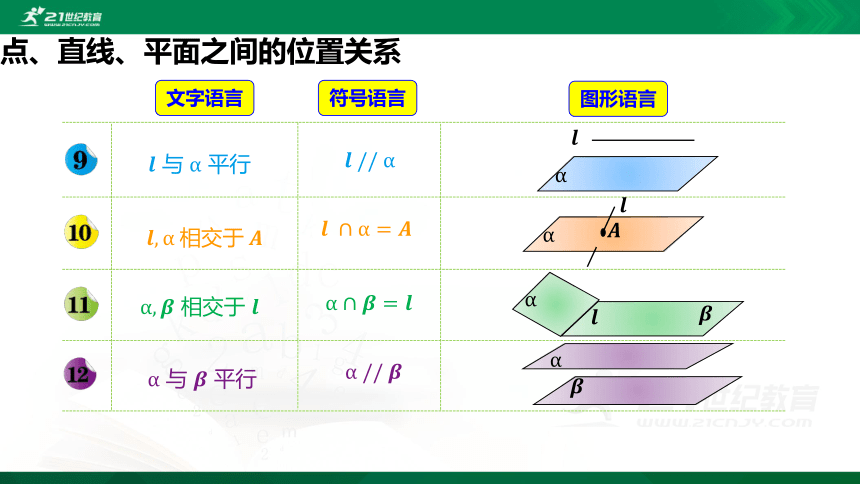
点、直线、平面之间的位置关系
???? 与 α 平行
?
文字语言
符号语言
图形语言
????,α?相交于?????
?
α,???? 相交于 ????
?
α 与 ???? 平行
?
?????//?α
?
????
?
?????∩α=????
?
????
?
α?//?????
?
????
?
α
?
α
?
α∩????=????
?
????
?
α
?
????
?
α
?
????
?
点、直线、平面之间的位置关系
文字语言,符号语言,图形语言的关系——
“点”可看做集合的元素,“直线”,“平面”均可看做点的集合.由此用符号表示时,点与直线、平面的关系用“∈”“?”表示;直线与平面的关系用“?”“?”表示.
?
①文字语言表述具体,易懂;符号语言简洁,易操作;图形语言形象生动
②三种语言可以互相转换,适用不同的情境
③用符号语言表示位置关系时,符号虽然来源于集合,但表达的仍是几何
意义.如“????∈????”表示的是“点????? 在直线 ???? 上”
?
平面的基本性质
图形语言——
符号语言—— ????,????,???? 三点不共线 ? 存在唯一的 ????,使 ????,????,????∈????
?
(1)基本事实①的条件为“过不在一条直线上的三点”,如果改为“过三个点”,则可能
存在无数个平面
基本事实①
过不在一条直线上的三个点,有且只有一个平面
????
?
????
?
????
?
α
?
应用——确定平面;判定两平面是否重合;证明点线共面
对基本事实①的理解
(2)基本事实①的结论为“有且只有一个平面”,“有”指存在性,“只有”指唯一性
探究新知
平面的基本性质
图形语言——
符号语言—— ????∈????,????∈????,且?????∈????,????∈??????????????
?
(1)直线是平面的真子集
基本事实②
如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.
????
?
????
?
????
?
α
?
应用——判断直线是否在平面内;判断点是否在平面内
对基本事实②的理解
(2)整条直线在平面内,则直线上的所有点都在平面内
平面的基本性质
图形语言——
符号语言—— ????∈????,且?????∈????
?
基本事实③
如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线
应用——判断直线是否在平面内;
判断点是否在平面内.
????
?
????
?
????
?
????
?
?????∩????=????,且?????∈????
?
①若两个相交平面有两个公共点,则过这两
点的直线就是相交平面的交线;
对基本事实③的理解:
②若两个相交平面有三个公共点,则这三点
共线;
③若两个平面相交,则一个平面内的直线与
另一平面的交点比在两平面的交线上;
④若两个不重合的平面有一个公共点,则这
两个平面相交.
基本事实①和基本事实②的三个推论
图形语言——
符号语言—— ??????????存在唯一的????,使?????∈????,?????????
?
推论①
经过一条直线和这条直线外一点,有且只有一个平面
文字语言——即相当于基本事实①中不共线三点中的两点连成
一条线与第三个点构成直线与直线外一点确定一
个平面.
????
?
????
?
α
?
探究新知
基本事实①和基本事实②的三个推论
图形语言—
符号语言—— ????∩????=?????存在唯一的????,使??????????,且??????????
?
推论②
经过两条相交直线,有且只有一个平面
文字语言——即相当于基本事实①中不共线三点中的两点连成
一条线与过这两个点中的其中一点和第三个点的
连线构成两条相交直线确定一个平面.
????
?
????
?
α
?
????
?
基本事实①和基本事实②的三个推论
图形语言——
符号语言—— ?????//??????存在唯一的????,使??????????,且??????????
?
推论③
经过两条平行直线,有且只有一个平面
文字语言——即相当于基本事实①中不共线三点中的两点连成
一条线与过第三个点作的与该直线平行的直线构
成两条平行直线确定一个平面.推理过程中直接
运用了两点确定一条直线及基本事实②.
????
?
α
?
????
?
应用基本事实或推论时忽略条件
已知A,B,C,D,E五点中,A,B,C,D共面,B,C,D,E共面,则A,B,C,D,E五点共面吗?为什么?
分两种情况来讨论:
①若B,C,D三点不共线,则它们确定一个平面α .
因为A,B,C,D共面,所以点A在平面α 内.
?
本题解题的时候很容易误认为A,B,C,D共面,所以点A在B,C,D确定的平面内,从而得出五点一定共面的结论. 忽略了“不在一条直线上的三点才能构成一个平面”这个重要条件.
因为B,C,D,E共面,所以点E在平面α内.所以点A,E都在平面α内,所以这五点共面.
?
②若B,C,D三点共线于????,若????∈????, ????∈????,则
A,B,C,D,E这五点一定共面,但平面不唯一.
?
若A,E中有且只有一个在????上,则五点一定共面.
?
若A,E都不在????上,则五点可能共面,可能不共面.
?
根据语句,画出相应的位置关系.
题①
——文字语言,符号语言,图形语言的转化
1A∈α,B?α
?
2?????????,????∩????=????,?????????
?
(1)点A在平面α内,点B不在平面α内,如图:
?
α
?
????
?
????
?
(2)直 ???? 在平面 ???? 内,直线 ???? 与平面 ???? 相交于点 ????,直线 ???? 不过点 ?????,如图:
?
α
?
????
?
????
?
????
?
有下列几个命题:①若ΔABC在平面 ???? 外,它的三条边所在的直线分别交平面 ???? 于 ????,????,????,则 ????,????,???? 三点共线; ②若两条直线 ????,???? 互相平行且分别交直线 ???? 于 ????,????两点,则这三条直线共面.
其中正确的有 ___________
?
题②
——平面性质基本事实及推论的应用
在①中,因为 ????,????,???? 三点既在平面 ???????????? 上,又在平面上,所以这三点比在平面与平面的交线上,即三点共线,①正确;
?
在②中,因为???? // ????,所以与确定一个平面 ????,而 ???? 上有两点????,???? 在该平面上,所以 ?????????,即 ????,????,???? 三线共面于 ????,所以②正确.
?
①
②
谢谢聆听
8.4.1 平 面
高中数学人教A版(2019)必修第二册
平面的概念与画法
【直观理解】课桌面、黑板面、教室平面、平静的水面都给我们以平面
的直观感觉,但它们都不是平面,而是平面的一部分.
【抽象理解】平面是平的,是无限延展的,没有厚薄,大小之分
平面的概念
平面与平面图形的区别和联系
平面是不可度量的;是无限延展,无厚薄,无大小的理想的面
我们日常接触到的是平面图形,如三角形,正方形,圆等,它们有大小之分,它们都不是平面,而是平面的一部分
我们可以用平面图形来表示平面
探究新知
平面的概念与画法
平面的画法
如果一个平面被另一个平面遮挡,那么被遮挡部分一般用虚线画出或者不画.
在立体几何中,平面通常画成一个平行四边形,当平面水平放置时,通常将平行四边形的锐角化成45°,且使横边长等于其邻边长的2倍;当平面竖直放置时,通常将平行四边形的一组对边画成铅垂线.
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
平面的概念与画法
平面的画法
相交平面示意图
立体几何画图或作辅助线的原则——
看得见的画成实线,看不见的画成虚线.即眼见为实,眼不见为虚.
平面的概念与画法
平面的表示
通常用平行四边形来表示平面.有时候也会用其他图形来表示平面,如三角形,矩形,梯形,圆等等.
①常用希腊字母 ????,????,???? 等表示平面,如平面 ????、
平面 ????、平面 ???? 等等.
?
②用大写英文字母表示平面,如对角线字母表
示平面,比如平面AC,平面BD等等.
③用平行四边形的四个顶点字母来表示平面,
如平面ABCD
④用平面内不共线的三个点来表示平面,如平面PHQ
用希腊字母α,β,γ等表示平面时,若已知条件说明了平面α,平面β,则之后可以省略“平面”二字;用大写英文字母表示的时候则不能省略.
?
点、直线、平面之间的位置关系
???? 在 ???? 上
?
文字语言
符号语言
图形语言
???? 在 ???? 外
?
???? 在 α 内
?
???? 在 α 外
?
????∈????
?
????
?
????
?
?????????
?
????
?
????
?
α
?
????∈α
?
????
?
?????α
?
α
?
????
?
探究新知
点、直线、平面之间的位置关系
???? 与 ???? 平行
?
文字语言
符号语言
图形语言
????,?????相交于?????
?
???? 与 ???? 异面
?
???? 在 α 内
?
?????//?????
?
????
?
????
?
?????∩?????=????
?
????
?
????
?
α
?
?????α
?
α
?
????
?
????
?
????
?
????
?
点、直线、平面之间的位置关系
???? 与 α 平行
?
文字语言
符号语言
图形语言
????,α?相交于?????
?
α,???? 相交于 ????
?
α 与 ???? 平行
?
?????//?α
?
????
?
?????∩α=????
?
????
?
α?//?????
?
????
?
α
?
α
?
α∩????=????
?
????
?
α
?
????
?
α
?
????
?
点、直线、平面之间的位置关系
文字语言,符号语言,图形语言的关系——
“点”可看做集合的元素,“直线”,“平面”均可看做点的集合.由此用符号表示时,点与直线、平面的关系用“∈”“?”表示;直线与平面的关系用“?”“?”表示.
?
①文字语言表述具体,易懂;符号语言简洁,易操作;图形语言形象生动
②三种语言可以互相转换,适用不同的情境
③用符号语言表示位置关系时,符号虽然来源于集合,但表达的仍是几何
意义.如“????∈????”表示的是“点????? 在直线 ???? 上”
?
平面的基本性质
图形语言——
符号语言—— ????,????,???? 三点不共线 ? 存在唯一的 ????,使 ????,????,????∈????
?
(1)基本事实①的条件为“过不在一条直线上的三点”,如果改为“过三个点”,则可能
存在无数个平面
基本事实①
过不在一条直线上的三个点,有且只有一个平面
????
?
????
?
????
?
α
?
应用——确定平面;判定两平面是否重合;证明点线共面
对基本事实①的理解
(2)基本事实①的结论为“有且只有一个平面”,“有”指存在性,“只有”指唯一性
探究新知
平面的基本性质
图形语言——
符号语言—— ????∈????,????∈????,且?????∈????,????∈??????????????
?
(1)直线是平面的真子集
基本事实②
如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.
????
?
????
?
????
?
α
?
应用——判断直线是否在平面内;判断点是否在平面内
对基本事实②的理解
(2)整条直线在平面内,则直线上的所有点都在平面内
平面的基本性质
图形语言——
符号语言—— ????∈????,且?????∈????
?
基本事实③
如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线
应用——判断直线是否在平面内;
判断点是否在平面内.
????
?
????
?
????
?
????
?
?????∩????=????,且?????∈????
?
①若两个相交平面有两个公共点,则过这两
点的直线就是相交平面的交线;
对基本事实③的理解:
②若两个相交平面有三个公共点,则这三点
共线;
③若两个平面相交,则一个平面内的直线与
另一平面的交点比在两平面的交线上;
④若两个不重合的平面有一个公共点,则这
两个平面相交.
基本事实①和基本事实②的三个推论
图形语言——
符号语言—— ??????????存在唯一的????,使?????∈????,?????????
?
推论①
经过一条直线和这条直线外一点,有且只有一个平面
文字语言——即相当于基本事实①中不共线三点中的两点连成
一条线与第三个点构成直线与直线外一点确定一
个平面.
????
?
????
?
α
?
探究新知
基本事实①和基本事实②的三个推论
图形语言—
符号语言—— ????∩????=?????存在唯一的????,使??????????,且??????????
?
推论②
经过两条相交直线,有且只有一个平面
文字语言——即相当于基本事实①中不共线三点中的两点连成
一条线与过这两个点中的其中一点和第三个点的
连线构成两条相交直线确定一个平面.
????
?
????
?
α
?
????
?
基本事实①和基本事实②的三个推论
图形语言——
符号语言—— ?????//??????存在唯一的????,使??????????,且??????????
?
推论③
经过两条平行直线,有且只有一个平面
文字语言——即相当于基本事实①中不共线三点中的两点连成
一条线与过第三个点作的与该直线平行的直线构
成两条平行直线确定一个平面.推理过程中直接
运用了两点确定一条直线及基本事实②.
????
?
α
?
????
?
应用基本事实或推论时忽略条件
已知A,B,C,D,E五点中,A,B,C,D共面,B,C,D,E共面,则A,B,C,D,E五点共面吗?为什么?
分两种情况来讨论:
①若B,C,D三点不共线,则它们确定一个平面α .
因为A,B,C,D共面,所以点A在平面α 内.
?
本题解题的时候很容易误认为A,B,C,D共面,所以点A在B,C,D确定的平面内,从而得出五点一定共面的结论. 忽略了“不在一条直线上的三点才能构成一个平面”这个重要条件.
因为B,C,D,E共面,所以点E在平面α内.所以点A,E都在平面α内,所以这五点共面.
?
②若B,C,D三点共线于????,若????∈????, ????∈????,则
A,B,C,D,E这五点一定共面,但平面不唯一.
?
若A,E中有且只有一个在????上,则五点一定共面.
?
若A,E都不在????上,则五点可能共面,可能不共面.
?
根据语句,画出相应的位置关系.
题①
——文字语言,符号语言,图形语言的转化
1A∈α,B?α
?
2?????????,????∩????=????,?????????
?
(1)点A在平面α内,点B不在平面α内,如图:
?
α
?
????
?
????
?
(2)直 ???? 在平面 ???? 内,直线 ???? 与平面 ???? 相交于点 ????,直线 ???? 不过点 ?????,如图:
?
α
?
????
?
????
?
????
?
有下列几个命题:①若ΔABC在平面 ???? 外,它的三条边所在的直线分别交平面 ???? 于 ????,????,????,则 ????,????,???? 三点共线; ②若两条直线 ????,???? 互相平行且分别交直线 ???? 于 ????,????两点,则这三条直线共面.
其中正确的有 ___________
?
题②
——平面性质基本事实及推论的应用
在①中,因为 ????,????,???? 三点既在平面 ???????????? 上,又在平面上,所以这三点比在平面与平面的交线上,即三点共线,①正确;
?
在②中,因为???? // ????,所以与确定一个平面 ????,而 ???? 上有两点????,???? 在该平面上,所以 ?????????,即 ????,????,???? 三线共面于 ????,所以②正确.
?
①
②
谢谢聆听
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
