8.3 简单几何体的表面积与体积(3)课件(共19张PPT)
文档属性
| 名称 | 8.3 简单几何体的表面积与体积(3)课件(共19张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-06 00:00:00 | ||
图片预览






文档简介
第8章 立体几何初步
8.3 简单几何体
的表面积与体积(3)
高中数学人教A版(2019)必修第二册
——柱体(棱柱、圆柱)的表面积与体积
[襄阳市2019高一期末]已知某个三棱柱的底面是正三角形,侧棱垂直于底面,它的侧面展开图是边长分别为6和4的矩形,求它的体积.
题①
由题意可知该三棱柱为正三棱柱,
∵ 正三棱柱的侧面展开图是边长分别为6和4的矩形,∴ 有如下两种情况:
① 6是底面周长,4是三棱柱的高,
此时底面积 ????1=????????×2×3=3,体积????1=????1?1=43
?
② 4是底面周长,6是三棱柱的高,
此时底面积 ????2=????????×????????×????3????=????3????,体积????1=????2?2=????3????
?
探究新知
将边长是1的正方形以其一边所在的直线为旋转轴旋
转一圈,所得几何体的表面积是多少?体积又是多少?
易知所得的几何体是一个底面圆半径为1的圆柱,则侧面积
????侧=2?????????
???????=2????×1×1
=2????
?
表面积????=????侧+2????底
=2????+2????=4????
?
求柱体(棱柱、圆柱)表面积的方法:
求棱柱的侧面积一般有两种方法,一是定义法,就是利用侧面积为各侧面积之和来求;二是公式法,直接用公式 ????圆柱=2????????(????+????) 来求解.
?
????圆柱侧=????????????????,????圆柱底=?????????????其中 ???? 为圆柱的底面半径, ???? 为圆柱的母线长.
?
针对练习
——锥体(棱锥、圆锥)的表面积与体积
已知棱长均为5,底面为正方形的四棱锥 ?????????????????????,如图,求它的侧面积、表面积和体积.
?
题②
因为四棱柱的各棱长均为5,所以各侧面都是全等的正三角形, 底面是边长为5的正方形.取????????的中点E,连接????????,????????,交于点????,连接????????,????????,
?
????侧=????????????????????????=????×????????????????·????????=????×????×?????????????????????=????????????
?
????
?
????
?
????
?
????
?
????
?
则????????⊥????????,如图所示,
?
????底=????正方形????????????????=????????=????????,????表面积=????底+????侧=????????+????????????
?
易得 ????????=????2????,所以????????=????2????,由正四棱锥的性质可知 ???????? 为正四棱锥的高
?
所以体积 ????=1????×????????×????2????=????????????2????
?
????
?
探究新知
若一个圆锥的轴截面是等边三角形,其面积为 3?,则这个圆锥的表面积是多少?
?
画出示意图所图所示,设圆锥的母线长为 ????,则由 ????????·????·3????????=3?,得 ????=????
?
所以圆锥的底面圆直径为 ?????,故圆锥的底面周长为 ????????,
?
①求棱锥表面积的一般方法:定义
法(注意“高”和“斜高”的区别)
圆锥的表面积
????=????×????????+????????×????????×????=????????
?
求椎体(棱锥、圆锥)表面积的方法:
②求椎体(棱锥、圆锥)体积的方法:利用椎体体积的公式 ????=????????????????计算.
?
针对练习
——台体(棱台、圆台)的表面积与体积
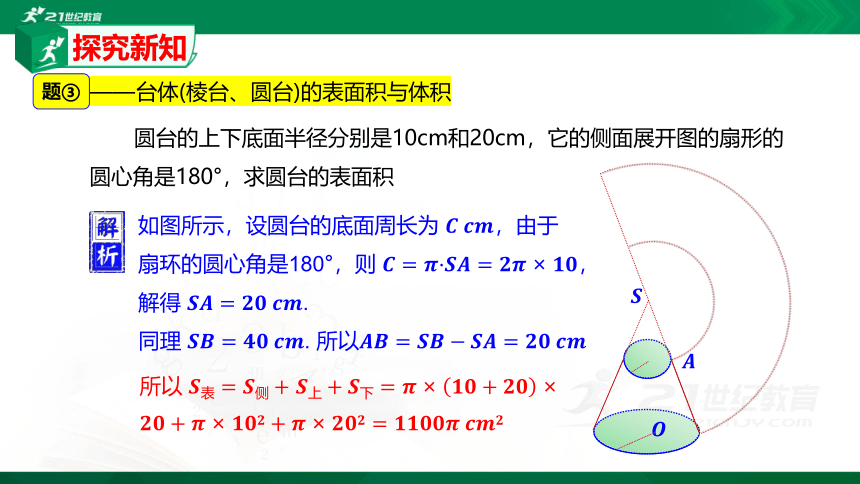
圆台的上下底面半径分别是10cm和20cm,它的侧面展开图的扇形的圆心角是180°,求圆台的表面积
题③
如图所示,设圆台的底面周长为 ?????????????,由于扇环的圆心角是180°,则 ????=????·????????=????????×????????,解得 ????????=?????????????????.
?
????
?
????
?
????
?
同理 ????????=?????????????????. 所以????????=?????????????????=?????????????????
?
所以 ????表= ????侧+ ????上+????下=????×????????+????????×????????+????×????????????+????×????????????=?????????????????????????????????
?
探究新知
①若圆台的体积为 ????????,上下底面的半径分别为1,2,则圆台的高是多少?
?
设圆台的高为 ????,由题意有,所以 ????=1????????+????????+????????????=????????,即????=????
?
②如图,圆台 ????????′ 的母线长为6,两底面半径分别为2和7,则此圆台的表面积是多少?
?
????′
?
????
?
由题意知上底面半径 ????′=????, 下底面半径 ????=????, 母线长 ????=????, 由圆台表面积公式可得:
?
????圆台表= ????侧+ ????上+????下
?
=????????????????
?
=????????′????+????????+????′????+????????
?
=????????????+????????+????×????+????×????
?
针对练习
——球的表面积与体积求解
①若一个球的大圆面积扩大为原来的2倍,那么这个球的体积扩大
为原来的多少倍?
题④
球的大圆面积扩大为原来的2倍,则球的半径扩大为原来的 ???? 倍,那么球的体积扩大为原来的 2???? 倍.
?
②若一个球的体积为 43?????,则它的表面积是多少?
?
设球的半径为 ?????,则 ????????????????????=????????????,所以 ????????=????????,????=????,
?
所以球的表面积 ????球=????????????????=????????????.
?
探究新知
①3个球的半径之比是1:2:3,那么最大的球的体积是其它两个球的体积和的 _______ .
由球的体积公式 ????球=?????????????????????,所以这3个球的体积之比是13:23:33=1:8:27,大球体积和两个小球体积之和的比是 27:(1+8)=3:1
?
②两个球的半径之比为2:3,那么这两个球的表面积之比是 _____ .
????:????
?
由球的体积公式 ????球=?????????????????,所以这2个球的表面积之比
????球????= ????球????= ????????????????????:????????????????????=????:????
?
????:????
?
针对练习
——求简单几何体的表面积
某几何体的直观图如图所示,则该几何体的
表面积是多少?
题⑤
由几何体的直观图知该几何体是长方体与半个圆柱的组合体,其中半圆柱的底面半径为2,高为4,长方体的棱长分别为4,2,2,所以该几何体的表面积
????=????????????×????????×????+????????????×????×????+????×????+????×????×????+????×????+????×????×??????
=????????+????????????.
?
探究新知
如图,在四边形 ???????????????? 中,∠????????????=????????°,∠????????????=????????????° ,????????=????,????????=????????,????????=?????,求四边形绕 ???????? 所在的直线旋转一周所成几何体的表面积和体积.
?
过点C作CE⊥AB于点E,讲四边形ABCD绕AB所在的直线旋转一周得到的几何体是由直角梯形ADCE旋转出的圆台和ΔCBE旋转出的圆锥拼接而成的组合体.
????
?
????
?
????
?
????
?
????
?
由题意及几何关系可知CE=4,AE=2,BE=3,BC=5.
????表=????×????????????+????????????+????????·????????+????·????????·????????=????????????+????????????????
?
????=????????????????????+????????·????????+????????????·????????+????????·????????????·????????=????????????????????
?
针对练习
——求简单组合体的体积
已知等腰直角三角形的直角边长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积是多少?
题⑥
绕等腰直角三角形的斜边所在的直线旋转一周形成的曲面围成的几何体为两个底面重合,等体积的圆锥,每一个圆锥的底面半径和高都是 ?????,所以所求几何体的体积
?
????=????×????????×????????×????=????????????????
?
探究新知
——球的截面问题
湖面上漂着一个小球,湖水结冰之后将球取出,冰面上留下了一个直径为6cm,深为1cm的空穴,则该球的半径是多少?
题⑦
设球心为 ????,???????? 是与冰面垂直的球的半径,冰面截球得到的小圆圆心为 ????,???????? 为小圆 ???? 的一条直径,设求的半径为 ????,则 ????????=?????????
?
所以球的表面积 ????=????????????????=????????×????????=?????????????????????????????
?
????
?
????
?
????
?
????
?
????
?
则 ?????????????+????????=????????,解得 ????=?????????????
?
探究新知
过球的一条半径的中点作垂直与该半径的平面,所得截面的面积与球的表面积的比是多少?
如图,过球心 ???? 作球的截面,设球的半径为 ????,截面圆的半径为 ????,则有
?
则截面圆的面积 ????截面=????????????????????=????????????????????
?
所以 ????截面????球=????????????????????????????????????=????????????·
?
????=?????????????????????=????????????
?
????????
?
????
?
????
?
????
?
针对练习
——球的切、接问题
有两个球,第一个球内切于正方体的6个面,第二个球与这个正方体的各条棱都相切,求这个两个球的表面积之比.
题⑧
设正方体的棱长为 ????,两个球的半径分别为 ???? 和 ????.
?
????
?
(1)正方体的内切球球心是正方体的中心,切点是六个面的中心,
如图所示,所以 ????????=?????,则 ????=????????????,所以此球的表面积
?
????
?
????
?
????
?
????????=????????????????=????????????
?
(2)球与正方体的各条棱的切点是每条棱的中点,过球心作正方
体的对角面,截面如图 ,所以 ????????=????????,则?????=????????????,所以此球的表面积
?
????????=????????????????=????????????????
?
,所以????????:????????=????????????:????????????????=????:????
?
探究新知
——平面图形旋转后得到的几何体的体积与表面积
如图的四边形ABCD是直角梯形,求图中阴影部分以AB所在直线为旋转轴旋转一周所成几何体的表面积.
题⑨
该平面图形旋转一周所得到的几何体是一个圆台挖掉半个球.由题意有
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????????????球=????????×????????×????????=?????????????????????
?
????圆台侧=????×????+????×?????????????+????????=?????????????????????????
?
????圆台下底=????×????????=?????????????????????????
?
所以该几何体的表面积为 ????????+????????????+????????????=?????????????????????????
?
探究新知
——几何体的体积或表面积的最值问题
已知底面是正六边形的六棱锥P-ABCDEF的七个顶点均在球????的表面上,底面正六边形的边长为1,若该六棱锥体积的最大值为3?,求球????的表面积.
?
题⑩
根据几何知识可知,当六棱锥P-ABCDEF为正六棱锥时,体积最大.
????底=????×????????×????×????×?????????????????????°=????????????,
?
∴ ????=????????????????=????,即 ????????×????????????=????,解得 ????=????
?
设六棱锥外接球的半径为R,可得所 ????????=????????+?????????????
?
∵底面正六边形的边长为1,∴底面外接圆的半径为1,正六棱锥的底面积
设正六棱锥的高为 ????,
?
解得????=????????,∴球????的表面积 ????表=????????????????=????????×????????????=????????????????
?
探究新知
谢谢聆听
8.3 简单几何体
的表面积与体积(3)
高中数学人教A版(2019)必修第二册
——柱体(棱柱、圆柱)的表面积与体积
[襄阳市2019高一期末]已知某个三棱柱的底面是正三角形,侧棱垂直于底面,它的侧面展开图是边长分别为6和4的矩形,求它的体积.
题①
由题意可知该三棱柱为正三棱柱,
∵ 正三棱柱的侧面展开图是边长分别为6和4的矩形,∴ 有如下两种情况:
① 6是底面周长,4是三棱柱的高,
此时底面积 ????1=????????×2×3=3,体积????1=????1?1=43
?
② 4是底面周长,6是三棱柱的高,
此时底面积 ????2=????????×????????×????3????=????3????,体积????1=????2?2=????3????
?
探究新知
将边长是1的正方形以其一边所在的直线为旋转轴旋
转一圈,所得几何体的表面积是多少?体积又是多少?
易知所得的几何体是一个底面圆半径为1的圆柱,则侧面积
????侧=2?????????
???????=2????×1×1
=2????
?
表面积????=????侧+2????底
=2????+2????=4????
?
求柱体(棱柱、圆柱)表面积的方法:
求棱柱的侧面积一般有两种方法,一是定义法,就是利用侧面积为各侧面积之和来求;二是公式法,直接用公式 ????圆柱=2????????(????+????) 来求解.
?
????圆柱侧=????????????????,????圆柱底=?????????????其中 ???? 为圆柱的底面半径, ???? 为圆柱的母线长.
?
针对练习
——锥体(棱锥、圆锥)的表面积与体积
已知棱长均为5,底面为正方形的四棱锥 ?????????????????????,如图,求它的侧面积、表面积和体积.
?
题②
因为四棱柱的各棱长均为5,所以各侧面都是全等的正三角形, 底面是边长为5的正方形.取????????的中点E,连接????????,????????,交于点????,连接????????,????????,
?
????侧=????????????????????????=????×????????????????·????????=????×????×?????????????????????=????????????
?
????
?
????
?
????
?
????
?
????
?
则????????⊥????????,如图所示,
?
????底=????正方形????????????????=????????=????????,????表面积=????底+????侧=????????+????????????
?
易得 ????????=????2????,所以????????=????2????,由正四棱锥的性质可知 ???????? 为正四棱锥的高
?
所以体积 ????=1????×????????×????2????=????????????2????
?
????
?
探究新知
若一个圆锥的轴截面是等边三角形,其面积为 3?,则这个圆锥的表面积是多少?
?
画出示意图所图所示,设圆锥的母线长为 ????,则由 ????????·????·3????????=3?,得 ????=????
?
所以圆锥的底面圆直径为 ?????,故圆锥的底面周长为 ????????,
?
①求棱锥表面积的一般方法:定义
法(注意“高”和“斜高”的区别)
圆锥的表面积
????=????×????????+????????×????????×????=????????
?
求椎体(棱锥、圆锥)表面积的方法:
②求椎体(棱锥、圆锥)体积的方法:利用椎体体积的公式 ????=????????????????计算.
?
针对练习
——台体(棱台、圆台)的表面积与体积
圆台的上下底面半径分别是10cm和20cm,它的侧面展开图的扇形的圆心角是180°,求圆台的表面积
题③
如图所示,设圆台的底面周长为 ?????????????,由于扇环的圆心角是180°,则 ????=????·????????=????????×????????,解得 ????????=?????????????????.
?
????
?
????
?
????
?
同理 ????????=?????????????????. 所以????????=?????????????????=?????????????????
?
所以 ????表= ????侧+ ????上+????下=????×????????+????????×????????+????×????????????+????×????????????=?????????????????????????????????
?
探究新知
①若圆台的体积为 ????????,上下底面的半径分别为1,2,则圆台的高是多少?
?
设圆台的高为 ????,由题意有,所以 ????=1????????+????????+????????????=????????,即????=????
?
②如图,圆台 ????????′ 的母线长为6,两底面半径分别为2和7,则此圆台的表面积是多少?
?
????′
?
????
?
由题意知上底面半径 ????′=????, 下底面半径 ????=????, 母线长 ????=????, 由圆台表面积公式可得:
?
????圆台表= ????侧+ ????上+????下
?
=????????????????
?
=????????′????+????????+????′????+????????
?
=????????????+????????+????×????+????×????
?
针对练习
——球的表面积与体积求解
①若一个球的大圆面积扩大为原来的2倍,那么这个球的体积扩大
为原来的多少倍?
题④
球的大圆面积扩大为原来的2倍,则球的半径扩大为原来的 ???? 倍,那么球的体积扩大为原来的 2???? 倍.
?
②若一个球的体积为 43?????,则它的表面积是多少?
?
设球的半径为 ?????,则 ????????????????????=????????????,所以 ????????=????????,????=????,
?
所以球的表面积 ????球=????????????????=????????????.
?
探究新知
①3个球的半径之比是1:2:3,那么最大的球的体积是其它两个球的体积和的 _______ .
由球的体积公式 ????球=?????????????????????,所以这3个球的体积之比是13:23:33=1:8:27,大球体积和两个小球体积之和的比是 27:(1+8)=3:1
?
②两个球的半径之比为2:3,那么这两个球的表面积之比是 _____ .
????:????
?
由球的体积公式 ????球=?????????????????,所以这2个球的表面积之比
????球????= ????球????= ????????????????????:????????????????????=????:????
?
????:????
?
针对练习
——求简单几何体的表面积
某几何体的直观图如图所示,则该几何体的
表面积是多少?
题⑤
由几何体的直观图知该几何体是长方体与半个圆柱的组合体,其中半圆柱的底面半径为2,高为4,长方体的棱长分别为4,2,2,所以该几何体的表面积
????=????????????×????????×????+????????????×????×????+????×????+????×????×????+????×????+????×????×??????
=????????+????????????.
?
探究新知
如图,在四边形 ???????????????? 中,∠????????????=????????°,∠????????????=????????????° ,????????=????,????????=????????,????????=?????,求四边形绕 ???????? 所在的直线旋转一周所成几何体的表面积和体积.
?
过点C作CE⊥AB于点E,讲四边形ABCD绕AB所在的直线旋转一周得到的几何体是由直角梯形ADCE旋转出的圆台和ΔCBE旋转出的圆锥拼接而成的组合体.
????
?
????
?
????
?
????
?
????
?
由题意及几何关系可知CE=4,AE=2,BE=3,BC=5.
????表=????×????????????+????????????+????????·????????+????·????????·????????=????????????+????????????????
?
????=????????????????????+????????·????????+????????????·????????+????????·????????????·????????=????????????????????
?
针对练习
——求简单组合体的体积
已知等腰直角三角形的直角边长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积是多少?
题⑥
绕等腰直角三角形的斜边所在的直线旋转一周形成的曲面围成的几何体为两个底面重合,等体积的圆锥,每一个圆锥的底面半径和高都是 ?????,所以所求几何体的体积
?
????=????×????????×????????×????=????????????????
?
探究新知
——球的截面问题
湖面上漂着一个小球,湖水结冰之后将球取出,冰面上留下了一个直径为6cm,深为1cm的空穴,则该球的半径是多少?
题⑦
设球心为 ????,???????? 是与冰面垂直的球的半径,冰面截球得到的小圆圆心为 ????,???????? 为小圆 ???? 的一条直径,设求的半径为 ????,则 ????????=?????????
?
所以球的表面积 ????=????????????????=????????×????????=?????????????????????????????
?
????
?
????
?
????
?
????
?
????
?
则 ?????????????+????????=????????,解得 ????=?????????????
?
探究新知
过球的一条半径的中点作垂直与该半径的平面,所得截面的面积与球的表面积的比是多少?
如图,过球心 ???? 作球的截面,设球的半径为 ????,截面圆的半径为 ????,则有
?
则截面圆的面积 ????截面=????????????????????=????????????????????
?
所以 ????截面????球=????????????????????????????????????=????????????·
?
????=?????????????????????=????????????
?
????????
?
????
?
????
?
????
?
针对练习
——球的切、接问题
有两个球,第一个球内切于正方体的6个面,第二个球与这个正方体的各条棱都相切,求这个两个球的表面积之比.
题⑧
设正方体的棱长为 ????,两个球的半径分别为 ???? 和 ????.
?
????
?
(1)正方体的内切球球心是正方体的中心,切点是六个面的中心,
如图所示,所以 ????????=?????,则 ????=????????????,所以此球的表面积
?
????
?
????
?
????
?
????????=????????????????=????????????
?
(2)球与正方体的各条棱的切点是每条棱的中点,过球心作正方
体的对角面,截面如图 ,所以 ????????=????????,则?????=????????????,所以此球的表面积
?
????????=????????????????=????????????????
?
,所以????????:????????=????????????:????????????????=????:????
?
探究新知
——平面图形旋转后得到的几何体的体积与表面积
如图的四边形ABCD是直角梯形,求图中阴影部分以AB所在直线为旋转轴旋转一周所成几何体的表面积.
题⑨
该平面图形旋转一周所得到的几何体是一个圆台挖掉半个球.由题意有
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????????????球=????????×????????×????????=?????????????????????
?
????圆台侧=????×????+????×?????????????+????????=?????????????????????????
?
????圆台下底=????×????????=?????????????????????????
?
所以该几何体的表面积为 ????????+????????????+????????????=?????????????????????????
?
探究新知
——几何体的体积或表面积的最值问题
已知底面是正六边形的六棱锥P-ABCDEF的七个顶点均在球????的表面上,底面正六边形的边长为1,若该六棱锥体积的最大值为3?,求球????的表面积.
?
题⑩
根据几何知识可知,当六棱锥P-ABCDEF为正六棱锥时,体积最大.
????底=????×????????×????×????×?????????????????????°=????????????,
?
∴ ????=????????????????=????,即 ????????×????????????=????,解得 ????=????
?
设六棱锥外接球的半径为R,可得所 ????????=????????+?????????????
?
∵底面正六边形的边长为1,∴底面外接圆的半径为1,正六棱锥的底面积
设正六棱锥的高为 ????,
?
解得????=????????,∴球????的表面积 ????表=????????????????=????????×????????????=????????????????
?
探究新知
谢谢聆听
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
