人教版三年级下册数学试题---《5 面积》压轴题综合练习 (含答案)
文档属性
| 名称 | 人教版三年级下册数学试题---《5 面积》压轴题综合练习 (含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 70.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-07 00:00:00 | ||
图片预览


文档简介
人教新版三年级下学期《5
面积》压轴同步卷
一.选择题(共10小题)
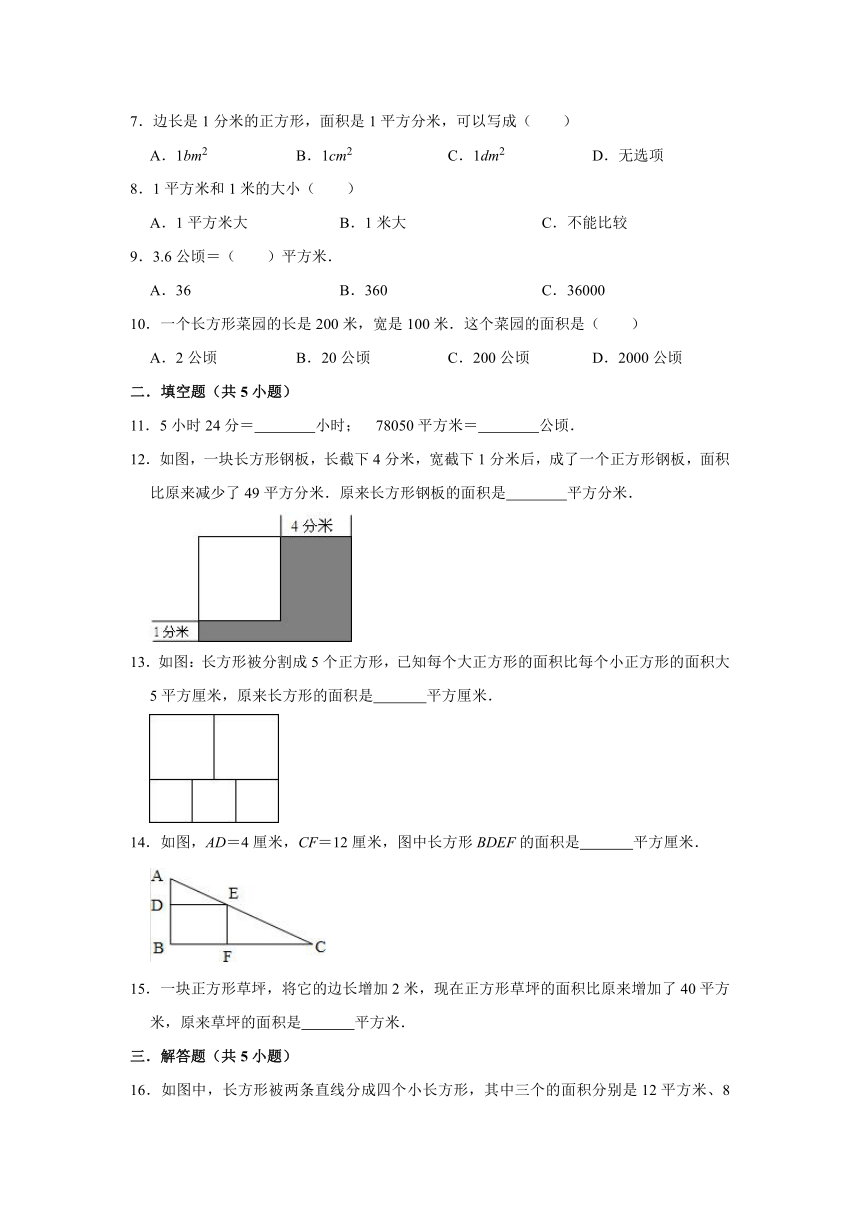
1.如图,两池拥挤程度相比较为( )
A.甲池拥挤
B.乙池拥挤
C.两池拥挤程度一样
D.无法确定
2.用两个边长是1厘米的正方形拼成一个长方形,这个长方形的面积是( )
A.6平方厘米
B.2平方厘米
C.1平方厘米
3.张大伯用24米篱笆靠一面墙围成一个长方形的养鸡栏(如图),要想围得最大面积,最大面积是( )平方米.
A.64
B.36
C.72
D.80
4.长方形的长增加,要使面积不变,宽必须减少( )
A.
B.
C.
5.比一比下面两个图形的面积.结果是( )
A.①>②
B.①<②
C.①=②
6.数学书的封面的面积是300( )
A.平方米
B.平方分米
C.平方厘米
7.边长是1分米的正方形,面积是1平方分米,可以写成( )
A.1bm2
B.1cm2
C.1dm2
D.无选项
8.1平方米和1米的大小( )
A.1平方米大
B.1米大
C.不能比较
9.3.6公顷=( )平方米.
A.36
B.360
C.36000
10.一个长方形菜园的长是200米,宽是100米.这个菜园的面积是( )
A.2公顷
B.20公顷
C.200公顷
D.2000公顷
二.填空题(共5小题)
11.5小时24分=
小时;
78050平方米=
公顷.
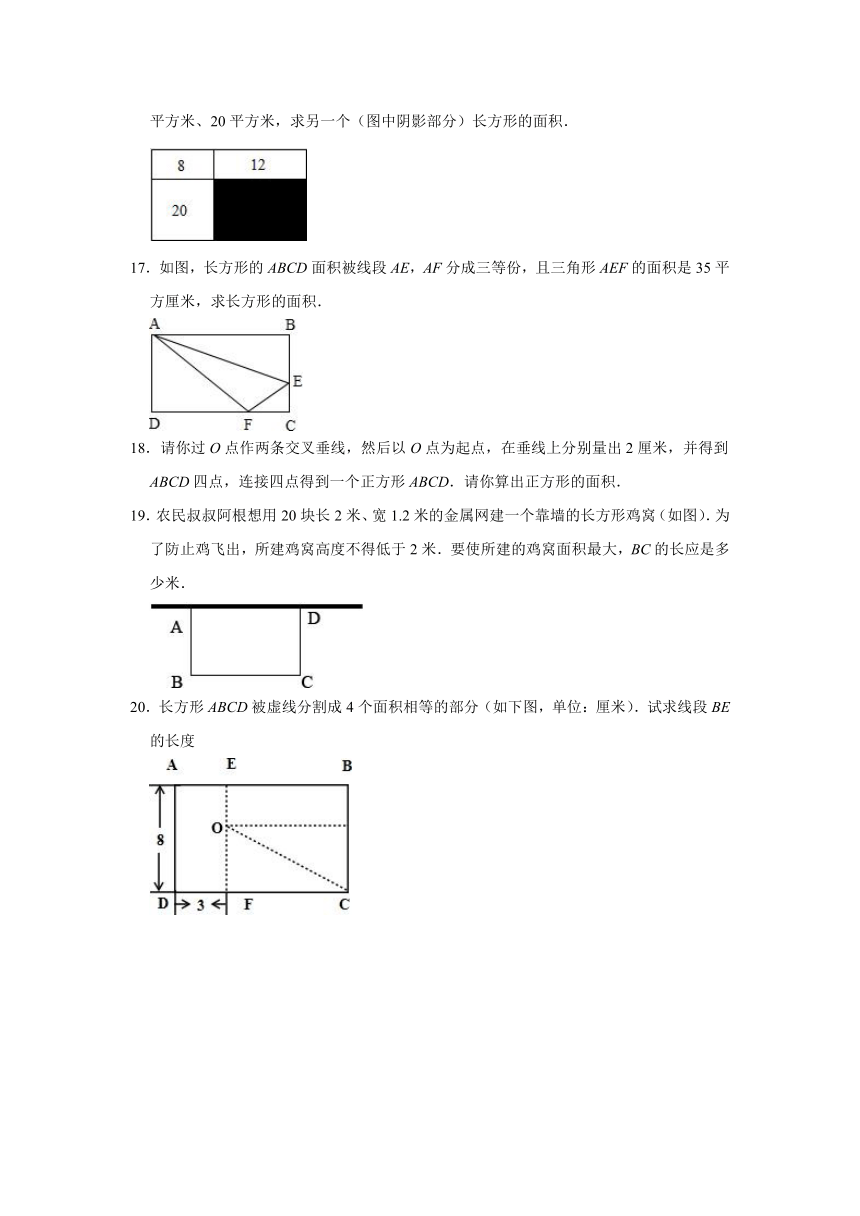
12.如图,一块长方形钢板,长截下4分米,宽截下1分米后,成了一个正方形钢板,面积比原来减少了49平方分米.原来长方形钢板的面积是
平方分米.
13.如图:长方形被分割成5个正方形,已知每个大正方形的面积比每个小正方形的面积大5平方厘米,原来长方形的面积是
平方厘米.
14.如图,AD=4厘米,CF=12厘米,图中长方形BDEF的面积是
平方厘米.
15.一块正方形草坪,将它的边长增加2米,现在正方形草坪的面积比原来增加了40平方米,原来草坪的面积是
平方米.
三.解答题(共5小题)
16.如图中,长方形被两条直线分成四个小长方形,其中三个的面积分别是12平方米、8平方米、20平方米,求另一个(图中阴影部分)长方形的面积.
17.如图,长方形的ABCD面积被线段AE,AF分成三等份,且三角形AEF的面积是35平方厘米,求长方形的面积.
18.请你过O点作两条交叉垂线,然后以O点为起点,在垂线上分别量出2厘米,并得到ABCD四点,连接四点得到一个正方形ABCD.请你算出正方形的面积.
19.农民叔叔阿根想用20块长2米、宽1.2米的金属网建一个靠墙的长方形鸡窝(如图).为了防止鸡飞出,所建鸡窝高度不得低于2米.要使所建的鸡窝面积最大,BC的长应是多少米.
20.长方形ABCD被虚线分割成4个面积相等的部分(如下图,单位:厘米).试求线段BE的长度
人教新版三年级下学期《5
面积》压轴同步卷
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:甲池:15×8÷30=4(平方米);
乙池:40×25÷200=5(平方米);
因为4<5,所以甲池比较拥挤;
故选:A.
2.【解答】解:1×1×2=2(平方厘米),
答:这个长方形的面积是2平方厘米.
故选:B.
3.【解答】解:设长方形的宽为a,则它的长为24﹣2a
因为长方形的长和宽约接近,则其面积越大.
所以长方形的宽应是6米,长是12米,
则此长方形的面积为:12×6=72(平方米).
故选:C.
4.【解答】解:设宽应该减少x,原长是2,宽是1,
2=2×(1+)×1×(1﹣x),
1=×(1﹣x),
1﹣x=,
x=,
所以要使面积不变,宽必须减少;
故选:B.
5.【解答】解:图①占4个小方格,图②占4个小方格,
所以图①=图②;
故选:C。
6.【解答】解:由分析可知:数学书的封面的面积是300平方厘米;
故选:C。
7.【解答】解:1×1=1(平方分米)=1dm2,
故选:C。
8.【解答】解:1平方米和1米的大小不是同类量,不能比较大小;
故选:C。
9.【解答】解:根据题意可得:
3.6×10000=36000;
所以3.6公顷=36000平方米.
故选:C.
10.【解答】解:100×200=20000(平方米)
20000平方米=2公顷
答:这个菜园的面积是2公顷.
故选:A.
二.填空题(共5小题)
11.【解答】解:5小时24分=5.4小时;
78050平方米=7.805公顷.
故答案为:5.4,7.805.
12.【解答】解:设正方形的边长为a分米,
则(a+1)×4+1×a=49,
4a+4+a=49,
5a+4=49,
5a+4﹣4=49﹣4,
5a=45,
5a÷5=45÷5,
a=9;
原来长方形的面积是:
(9+4)×(9+1),
=13×10,
=130(平方分米);
答:原来长方形钢板的面积是130平方分米.
故答案为:130.
13.【解答】解:因为每个大正方形比每个小正方形面积大5平方厘米,
所以就是1.25(即:2.25﹣1)个小正方形的面积是5平方厘米;
即一个小正方形的面积是:5÷1.25=4(平方厘米);
所以一个大正方形的面积是2.25×4=9(平方厘米);
所以长方形总面积:4×3+9×2=30(平方厘米);
答:原来长方形的面积是30平方厘米.
故答案为:30.
14.【解答】解:设长方形的长为a厘米,宽为b厘米,由题意得:
ab=(4+b)×(12+a)÷2﹣4a÷2﹣12b÷2,
ab=(48+4a+12b+ab)÷2﹣2a﹣6b,
ab=24+2a+6b+ab﹣2a﹣6b,
ab﹣ab=24,
=24,
ab=24×2,
ab=48.
所以长方形BDEF的面积是48平方厘米.
故答案为:48.
15.【解答】解:图①的面积是:
2×2=4(平方米);
图②、图③每个长方形的面积:
(40﹣4)÷2,
=36÷2,
=18(平方米);
原来正方形的边长:
18÷2=9(米);
原来这个草坪的面积是:
9×9=81(平方米);
答:原来这个草坪的面积是81平方米.
故答案为:81.
三.解答题(共5小题)
16.【解答】解:设最小的长方形的长为a米,则宽为米,
则阴影部分的面积是:
×(12÷)
=
=30(平方米)
答:阴影部分的面积是30平方米.
17.【解答】解:根据以上分析知:S△EFC=EC×CF=×BC×CD=BC×CD=×ABCD的面积,
四边形AECF的面积=×ABCD的面积,
设长方形ABCD的面积为S,根据题意得:
(﹣)×S=35
S=35,
S=126.
答:这个长方形的面积是126平方厘米.
18.【解答】解:如图所示:
正方形的面积为:×2×2×4=8平方厘米,
答:正方形的面积是8平方厘米.
19.【解答】解:设长方形的宽边AB为x米,长边BC为2x米,
(x+2x+x)=20×1.2,
4x=24,
x=6,
长边BC是6×2=12米,而12和6恰好是1.2的整数倍,所以围成长方形的面积最大是12×6=72平方米;也就是说,围成一个长方形,围三面,长边围10块,宽边围5块,这样围出的面积最大.
答:BC的长应是12米.
20.【解答】解:设FO=x厘米,CF=y厘米,
因为4个面积相等,
所以CF×FO=3×8×2=48(平方厘米),
即xy=48
EO×EB=3×8=24(平方厘米)
即(8﹣x)×y=3×8,
8y﹣xy=24,
8y=24+xy,
8y=24+48,
8y=72,
y=9,
即BE=9厘米;
答:线段BE的长是9厘米.
面积》压轴同步卷
一.选择题(共10小题)
1.如图,两池拥挤程度相比较为( )
A.甲池拥挤
B.乙池拥挤
C.两池拥挤程度一样
D.无法确定
2.用两个边长是1厘米的正方形拼成一个长方形,这个长方形的面积是( )
A.6平方厘米
B.2平方厘米
C.1平方厘米
3.张大伯用24米篱笆靠一面墙围成一个长方形的养鸡栏(如图),要想围得最大面积,最大面积是( )平方米.
A.64
B.36
C.72
D.80
4.长方形的长增加,要使面积不变,宽必须减少( )
A.
B.
C.
5.比一比下面两个图形的面积.结果是( )
A.①>②
B.①<②
C.①=②
6.数学书的封面的面积是300( )
A.平方米
B.平方分米
C.平方厘米
7.边长是1分米的正方形,面积是1平方分米,可以写成( )
A.1bm2
B.1cm2
C.1dm2
D.无选项
8.1平方米和1米的大小( )
A.1平方米大
B.1米大
C.不能比较
9.3.6公顷=( )平方米.
A.36
B.360
C.36000
10.一个长方形菜园的长是200米,宽是100米.这个菜园的面积是( )
A.2公顷
B.20公顷
C.200公顷
D.2000公顷
二.填空题(共5小题)
11.5小时24分=
小时;
78050平方米=
公顷.
12.如图,一块长方形钢板,长截下4分米,宽截下1分米后,成了一个正方形钢板,面积比原来减少了49平方分米.原来长方形钢板的面积是
平方分米.
13.如图:长方形被分割成5个正方形,已知每个大正方形的面积比每个小正方形的面积大5平方厘米,原来长方形的面积是
平方厘米.
14.如图,AD=4厘米,CF=12厘米,图中长方形BDEF的面积是
平方厘米.
15.一块正方形草坪,将它的边长增加2米,现在正方形草坪的面积比原来增加了40平方米,原来草坪的面积是
平方米.
三.解答题(共5小题)
16.如图中,长方形被两条直线分成四个小长方形,其中三个的面积分别是12平方米、8平方米、20平方米,求另一个(图中阴影部分)长方形的面积.
17.如图,长方形的ABCD面积被线段AE,AF分成三等份,且三角形AEF的面积是35平方厘米,求长方形的面积.
18.请你过O点作两条交叉垂线,然后以O点为起点,在垂线上分别量出2厘米,并得到ABCD四点,连接四点得到一个正方形ABCD.请你算出正方形的面积.
19.农民叔叔阿根想用20块长2米、宽1.2米的金属网建一个靠墙的长方形鸡窝(如图).为了防止鸡飞出,所建鸡窝高度不得低于2米.要使所建的鸡窝面积最大,BC的长应是多少米.
20.长方形ABCD被虚线分割成4个面积相等的部分(如下图,单位:厘米).试求线段BE的长度
人教新版三年级下学期《5
面积》压轴同步卷
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:甲池:15×8÷30=4(平方米);
乙池:40×25÷200=5(平方米);
因为4<5,所以甲池比较拥挤;
故选:A.
2.【解答】解:1×1×2=2(平方厘米),
答:这个长方形的面积是2平方厘米.
故选:B.
3.【解答】解:设长方形的宽为a,则它的长为24﹣2a
因为长方形的长和宽约接近,则其面积越大.
所以长方形的宽应是6米,长是12米,
则此长方形的面积为:12×6=72(平方米).
故选:C.
4.【解答】解:设宽应该减少x,原长是2,宽是1,
2=2×(1+)×1×(1﹣x),
1=×(1﹣x),
1﹣x=,
x=,
所以要使面积不变,宽必须减少;
故选:B.
5.【解答】解:图①占4个小方格,图②占4个小方格,
所以图①=图②;
故选:C。
6.【解答】解:由分析可知:数学书的封面的面积是300平方厘米;
故选:C。
7.【解答】解:1×1=1(平方分米)=1dm2,
故选:C。
8.【解答】解:1平方米和1米的大小不是同类量,不能比较大小;
故选:C。
9.【解答】解:根据题意可得:
3.6×10000=36000;
所以3.6公顷=36000平方米.
故选:C.
10.【解答】解:100×200=20000(平方米)
20000平方米=2公顷
答:这个菜园的面积是2公顷.
故选:A.
二.填空题(共5小题)
11.【解答】解:5小时24分=5.4小时;
78050平方米=7.805公顷.
故答案为:5.4,7.805.
12.【解答】解:设正方形的边长为a分米,
则(a+1)×4+1×a=49,
4a+4+a=49,
5a+4=49,
5a+4﹣4=49﹣4,
5a=45,
5a÷5=45÷5,
a=9;
原来长方形的面积是:
(9+4)×(9+1),
=13×10,
=130(平方分米);
答:原来长方形钢板的面积是130平方分米.
故答案为:130.
13.【解答】解:因为每个大正方形比每个小正方形面积大5平方厘米,
所以就是1.25(即:2.25﹣1)个小正方形的面积是5平方厘米;
即一个小正方形的面积是:5÷1.25=4(平方厘米);
所以一个大正方形的面积是2.25×4=9(平方厘米);
所以长方形总面积:4×3+9×2=30(平方厘米);
答:原来长方形的面积是30平方厘米.
故答案为:30.
14.【解答】解:设长方形的长为a厘米,宽为b厘米,由题意得:
ab=(4+b)×(12+a)÷2﹣4a÷2﹣12b÷2,
ab=(48+4a+12b+ab)÷2﹣2a﹣6b,
ab=24+2a+6b+ab﹣2a﹣6b,
ab﹣ab=24,
=24,
ab=24×2,
ab=48.
所以长方形BDEF的面积是48平方厘米.
故答案为:48.
15.【解答】解:图①的面积是:
2×2=4(平方米);
图②、图③每个长方形的面积:
(40﹣4)÷2,
=36÷2,
=18(平方米);
原来正方形的边长:
18÷2=9(米);
原来这个草坪的面积是:
9×9=81(平方米);
答:原来这个草坪的面积是81平方米.
故答案为:81.
三.解答题(共5小题)
16.【解答】解:设最小的长方形的长为a米,则宽为米,
则阴影部分的面积是:
×(12÷)
=
=30(平方米)
答:阴影部分的面积是30平方米.
17.【解答】解:根据以上分析知:S△EFC=EC×CF=×BC×CD=BC×CD=×ABCD的面积,
四边形AECF的面积=×ABCD的面积,
设长方形ABCD的面积为S,根据题意得:
(﹣)×S=35
S=35,
S=126.
答:这个长方形的面积是126平方厘米.
18.【解答】解:如图所示:
正方形的面积为:×2×2×4=8平方厘米,
答:正方形的面积是8平方厘米.
19.【解答】解:设长方形的宽边AB为x米,长边BC为2x米,
(x+2x+x)=20×1.2,
4x=24,
x=6,
长边BC是6×2=12米,而12和6恰好是1.2的整数倍,所以围成长方形的面积最大是12×6=72平方米;也就是说,围成一个长方形,围三面,长边围10块,宽边围5块,这样围出的面积最大.
答:BC的长应是12米.
20.【解答】解:设FO=x厘米,CF=y厘米,
因为4个面积相等,
所以CF×FO=3×8×2=48(平方厘米),
即xy=48
EO×EB=3×8=24(平方厘米)
即(8﹣x)×y=3×8,
8y﹣xy=24,
8y=24+xy,
8y=24+48,
8y=72,
y=9,
即BE=9厘米;
答:线段BE的长是9厘米.
